














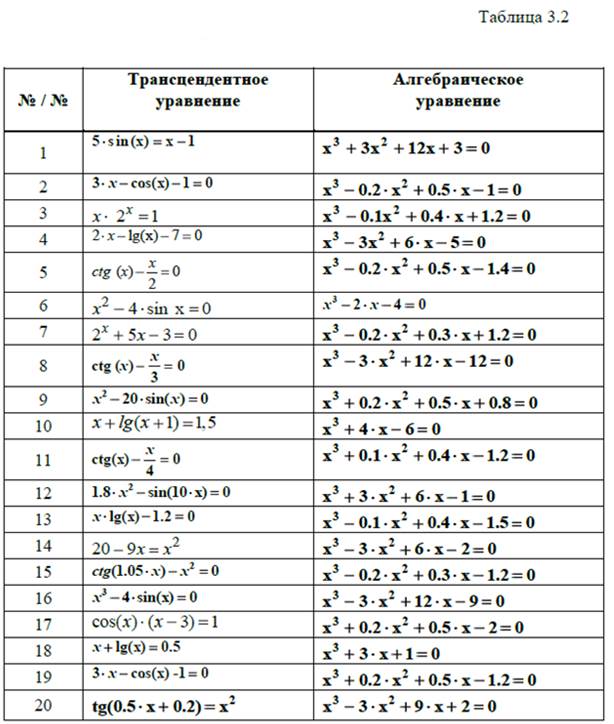
Практическая работа №2 – Способы решения нелинейных уравнений, методы локализации и уточнения корней нелинейных уравнений


Раздел 2. Методы решений систем уравнений
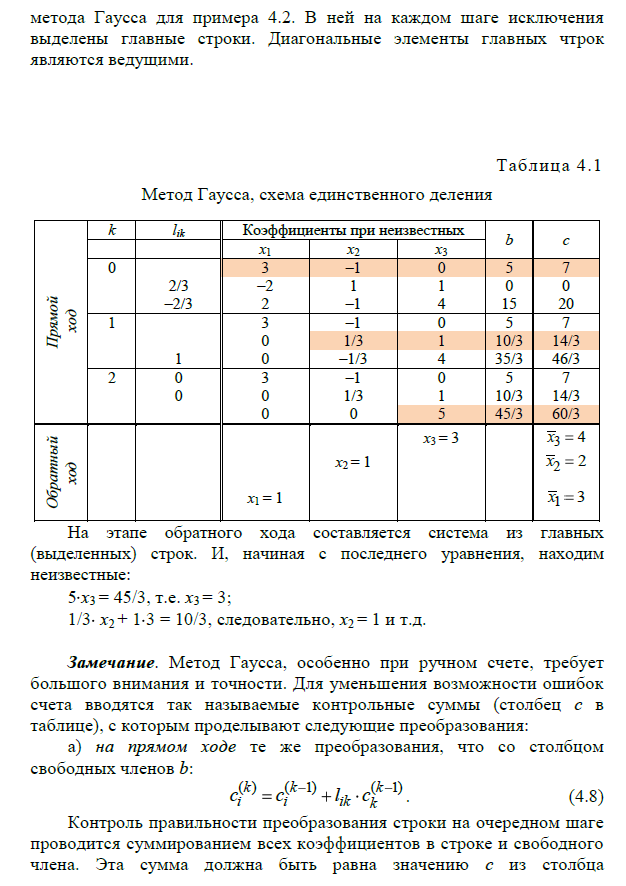
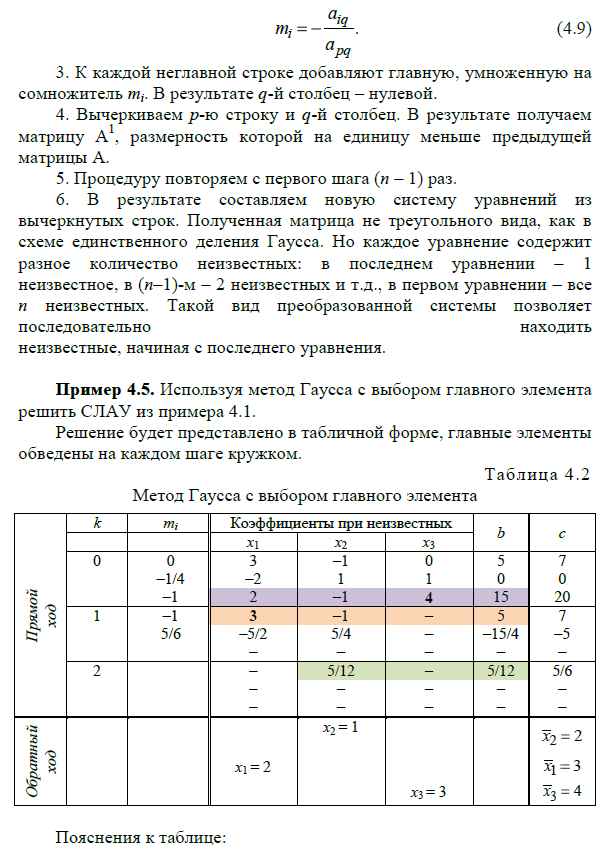
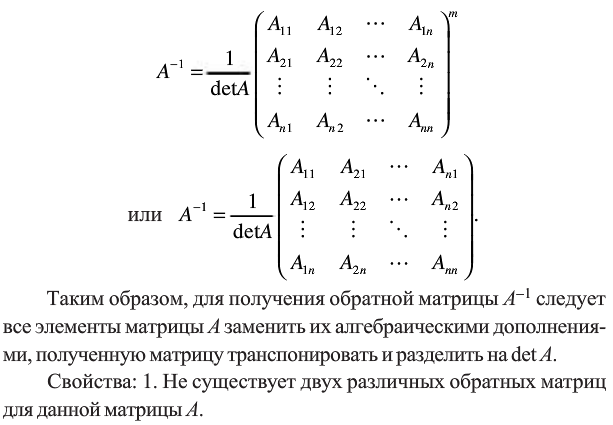
Практическая работа №3 – Количество операций методов Крамера о обратной матрицы; метод Гаусса и его модификации
















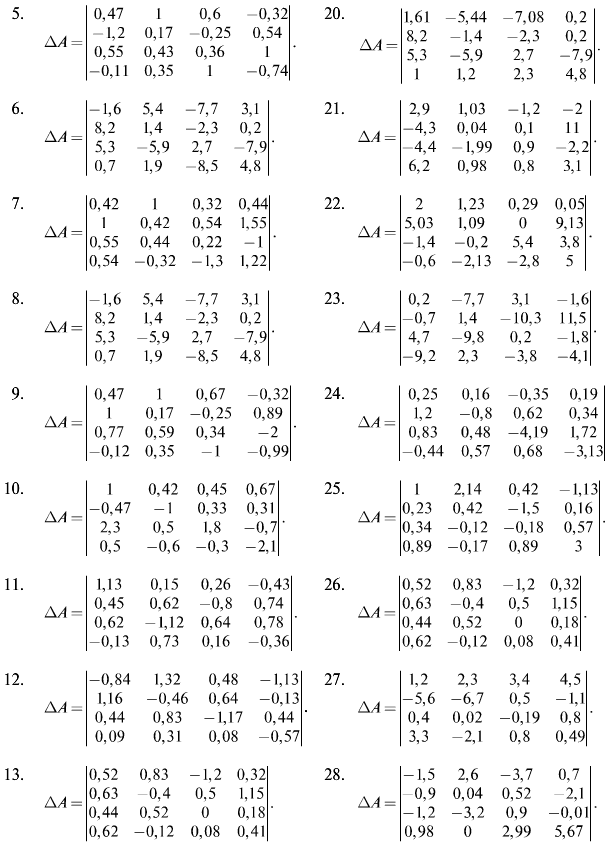


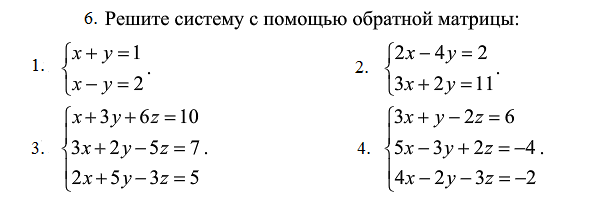
Практическая работа №4 – Матричные и векторные нормы; классификация итерационных процессов; метод простой итерации; метод Якоби; метод Зейделя 

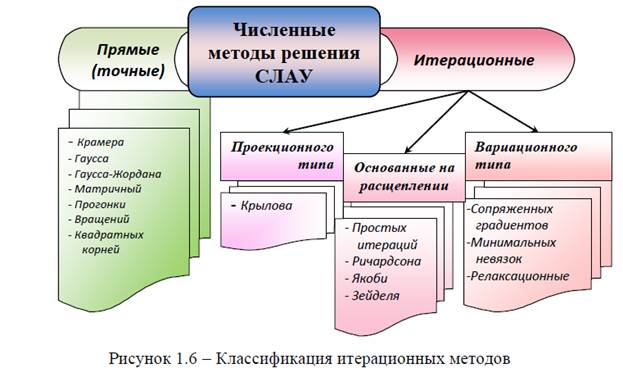
Общая классификация итерационных методов представлена на рисунке 1.6
Итерационные методы делятся на несколько типов в зависимости от применяемого подхода:
- Проекционного типа:
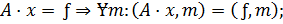
- Основанные на расщеплении:
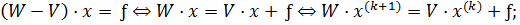
- Вариационного типа:
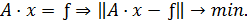

















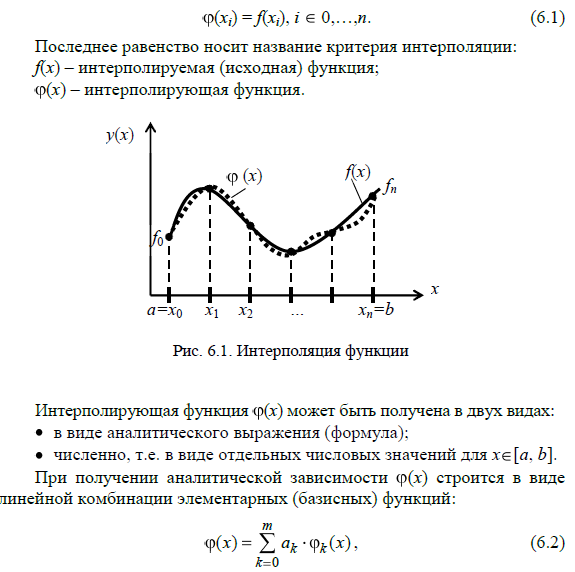
Раздел 3. Интерполирование функций
Практическая работа №5 – Сеточные функции, полином Лагранжа и полином Ньютона, их сравнение





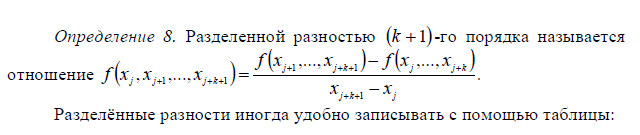











Практическая работа №6 – Понятие сплайна, алгоритм нахождения коэффициентов сплайна, графическая интерпретация результатов интерполирования





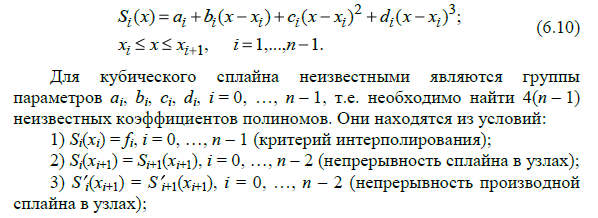






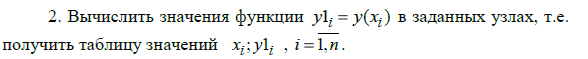


Раздел 4. Численное дифференцирование и интегрирование
Практическая работа №7 – Формулы вычисления численных производных первого и второго порядков






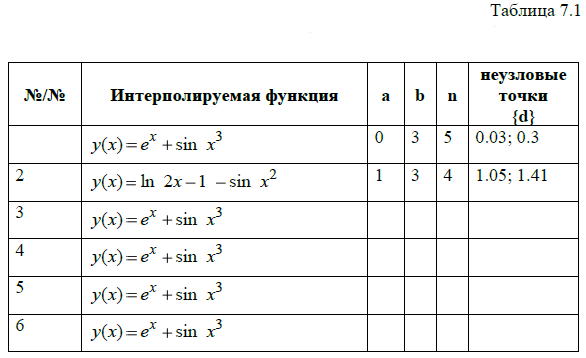
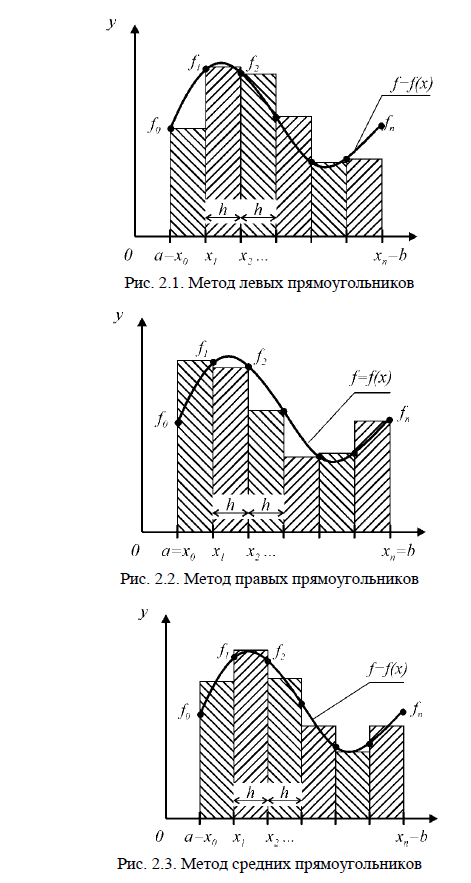
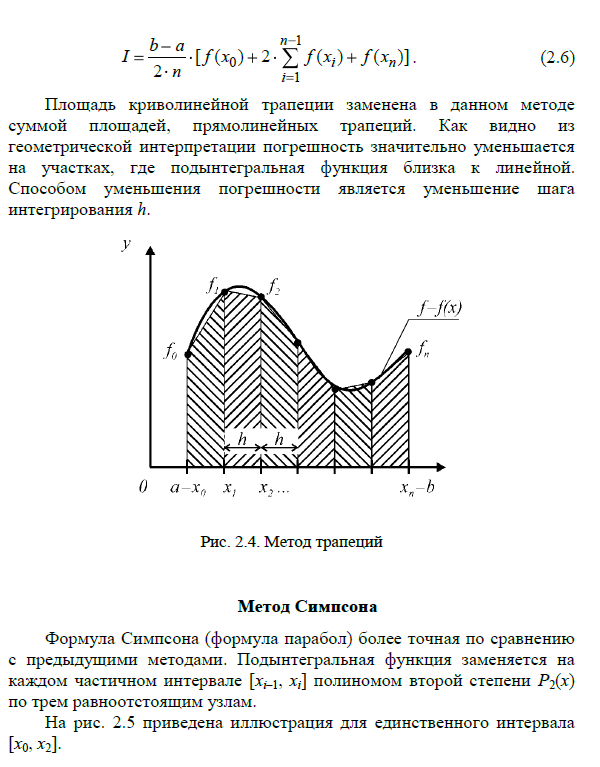
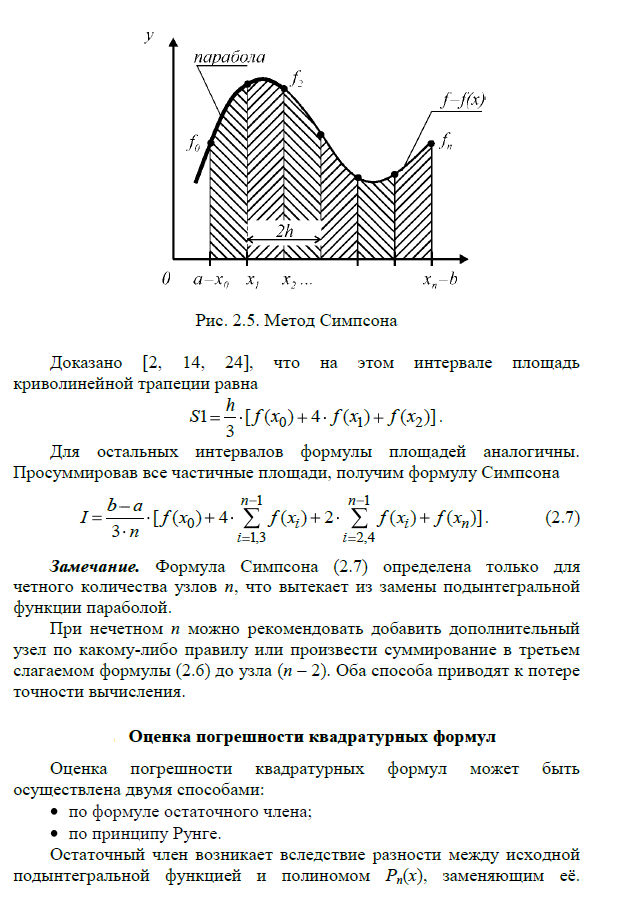
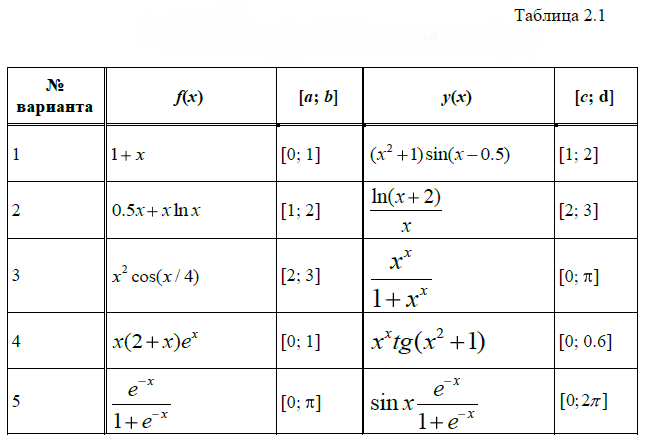
Практическая работа №8 – Квадратурные формулы прямоугольников, трапеций, метод Симпсона численного интегрирования














Раздел 5. Численное решение дифференциальных уравнений
Практическая работа №9 – Способы реализации метода Эйлера-Коши и его погрешность


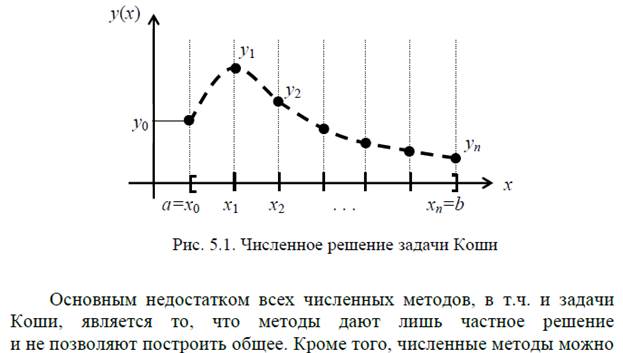



 Решение дифференциального уравнения – функция y0(xk).
Решение дифференциального уравнения – функция y0(xk).

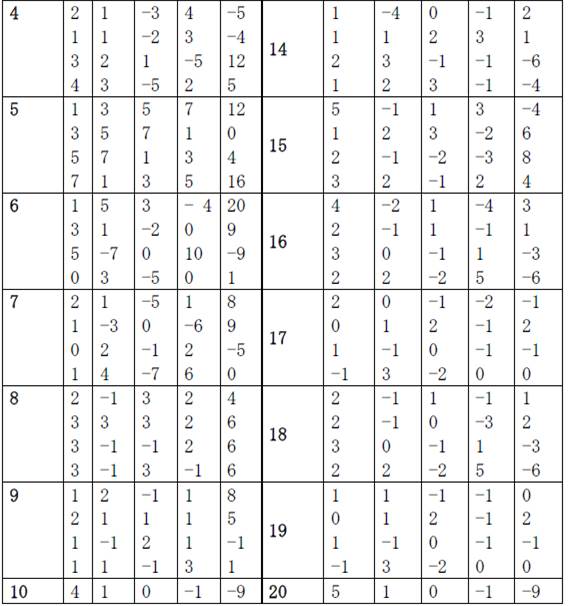
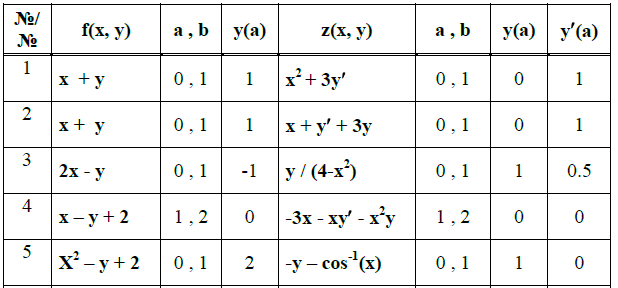
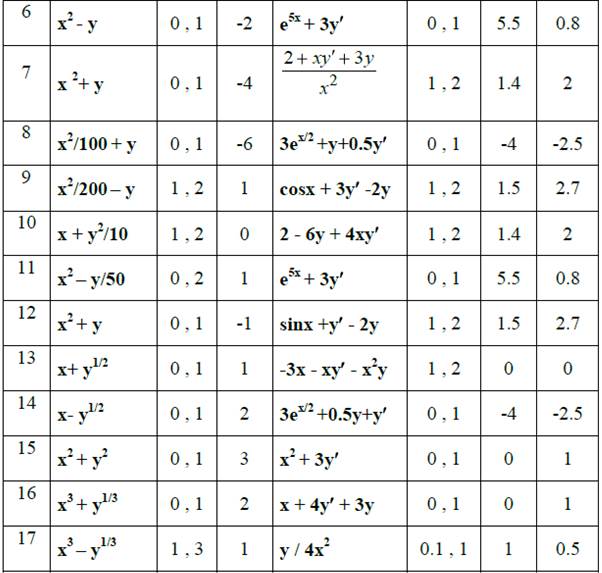
Таблица 6.1
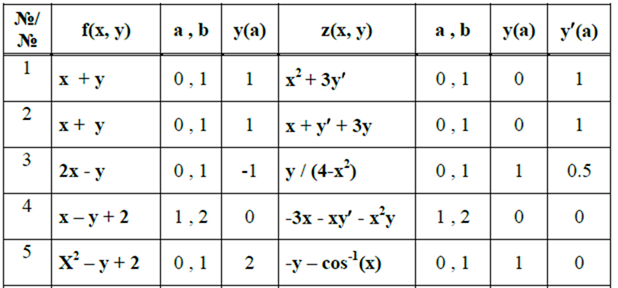
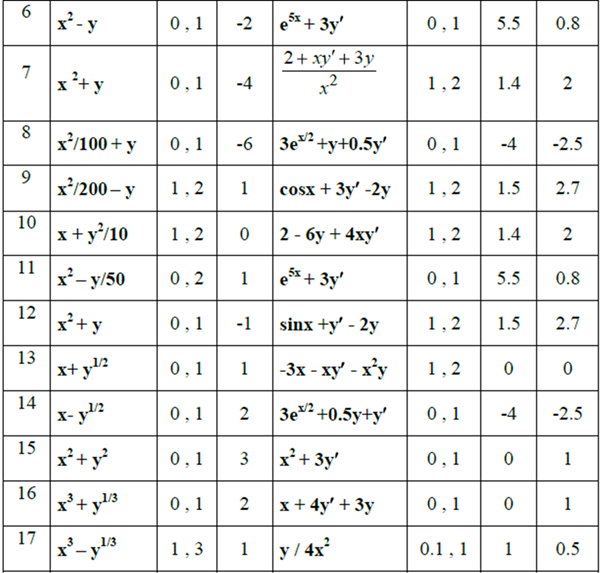
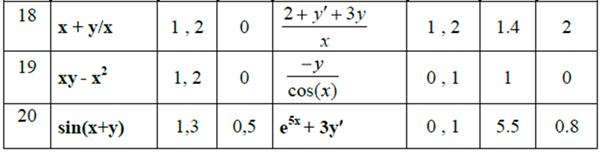
Практическая работа №10 – Реализация метода Рунге-Кутта 


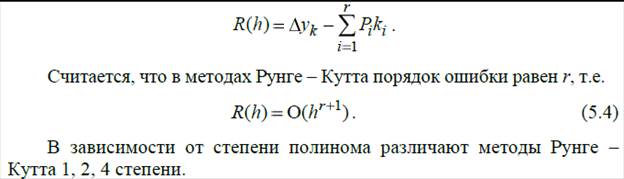

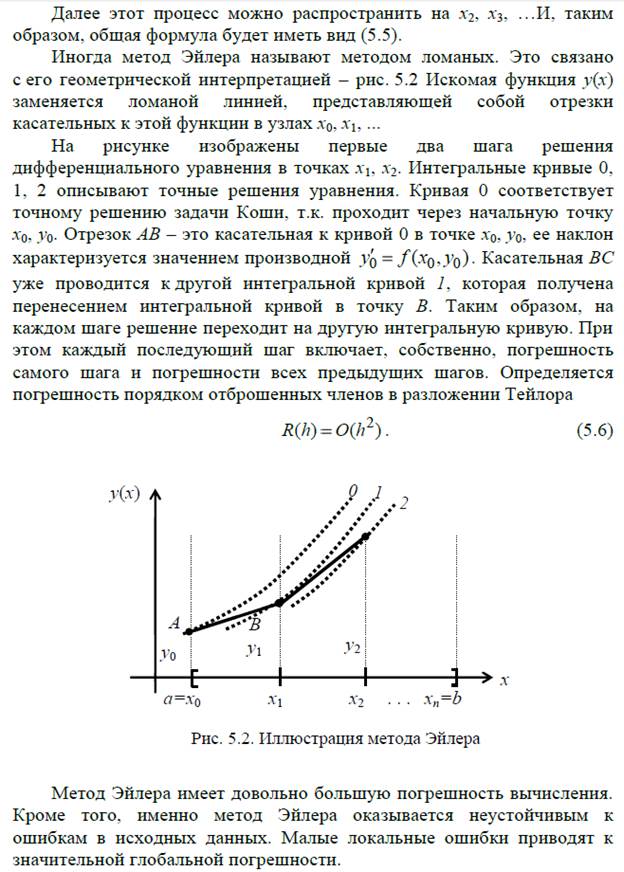

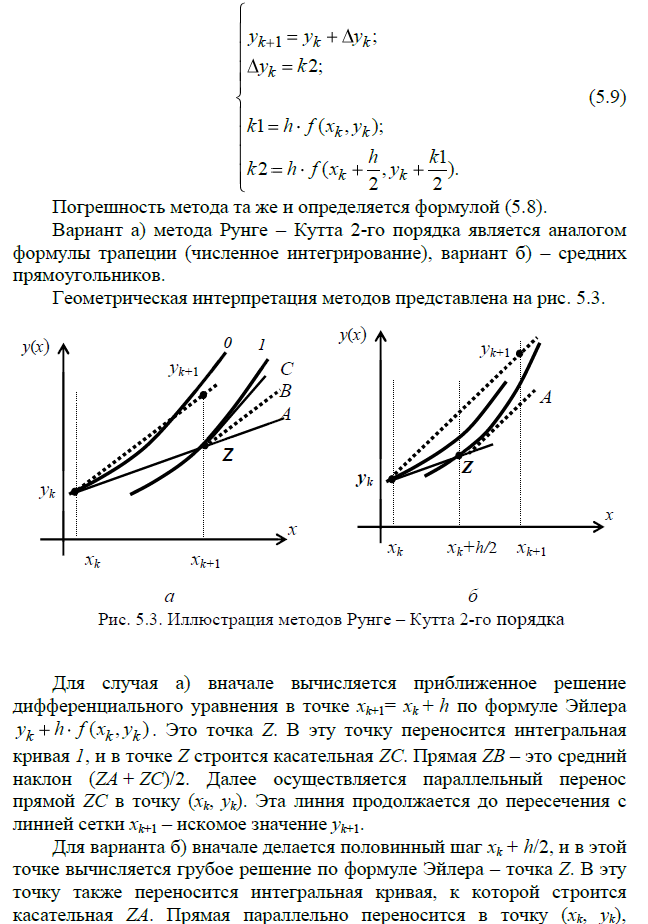


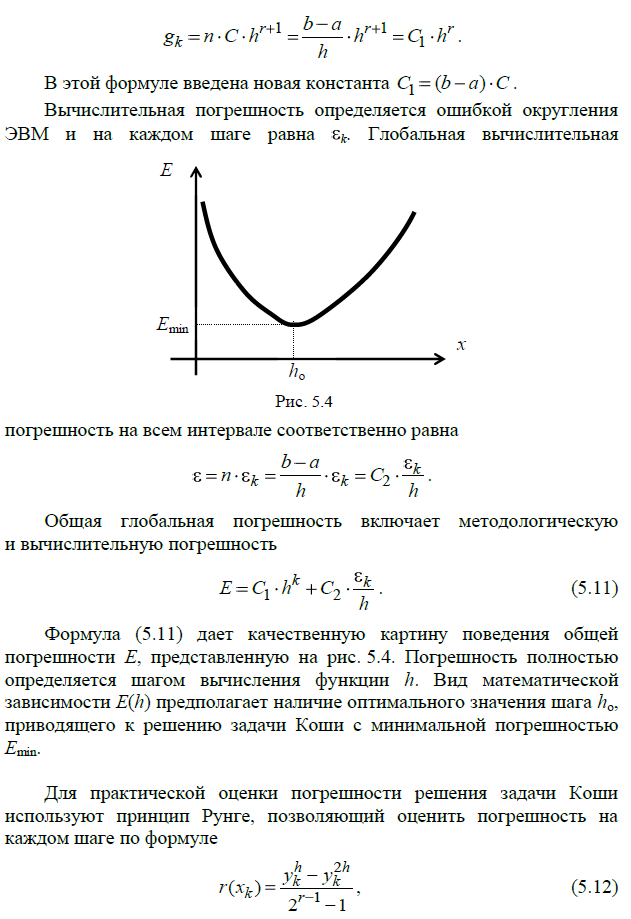



Таблица 6.1
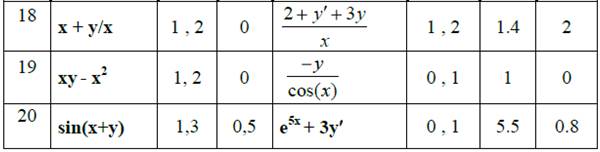
Библиографический список
Основная литература:
1. Вычислительная математика. Часть 1 [Электронный ресурс]: учебное пособие/ В.Н. Варапаев [и др.].— Электрон. текстовые данные.— М.: Московский государственный строительный университет, Ай Пи Эр Медиа, ЭБС АСВ, 2017.— 88 c.— Режим доступа: http://www.iprbookshop.ru/60773.— ЭБС «IPRbooks»
2. Сагадеева М.А. Вычислительная математика. Практикум : учеб. пособие / М. А. Сагадеева ; Южно-Уральский институт управления и экономики. - Челябинск : Violitprint, 2016. - 42 с
3. Чикуров Н.Г. Моделирование систем и процессов : учеб. пособие для студ. вузов / Н. Г. Чикуров. - М. : РИОР, 2015. - 398 с. - (Высшее образование)
Дополнительная литература:
1. Математика. Дискретная математика [Электронный ресурс]: учебник/ В.Ф. Золотухин [и др.].— Электрон. текстовые данные.— Ростов-на-Дону: Институт водного транспорта имени Г.Я. Седова – филиал «Государственный морской университет имени адмирала Ф.Ф. Ушакова», 2016.— 129 c.— Режим доступа: http://www.iprbookshop.ru/57348.html.— ЭБС «IPRbooks»
2. Попов А.М. Экономико-математические методы и модели : учебник для прикладного бакалавриата / А. М. Попов, В. Н. Сотников. - 3-е изд., испр. и доп. - М. : Юрайт, 2016. - 345 с. - (Бакалавр. Прикладной курс)
3. Экономико-математические методы и модели : учебник для прикладного бакалавриата / А. М. Попов, В. Н. Сотников. - 3-е изд., испр. и доп. - М. : Юрайт, 2016. - 345 с. - (Бакалавр. Прикладной курс)
[1] Описываются задачи по видам деятельности, которые указываются в ФГОС по данному направлению (специальности) в соответствии с разделом IV «Характеристика профессиональной деятельности бакалавра (магистра / специалиста) ».
[2] Каждый преподаватель прописывает этот раздел самостоятельно
Дата: 2018-12-28, просмотров: 414.