Электростатика
Законы постоянного тока
Колебания волны
Оптика
Атомная и ядерная физика
Подготовить к четвергу
Механика:
Кинематика
Основные понятия кинематики
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно (см 1.2) Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.
Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.
В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.
В системе СГС (Сантиметр, грамм, секунда) приняты соответственно сантиметр и секунда.
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела.
Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Колесо обозрения», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.
Понятие материальной точки играет важную роль в механике.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = 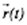 y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени
y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени
радиус-вектора 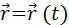 (векторный способ), проведенного из
(векторный способ), проведенного из
начала координат до данной точки (рис. 1.1.1).
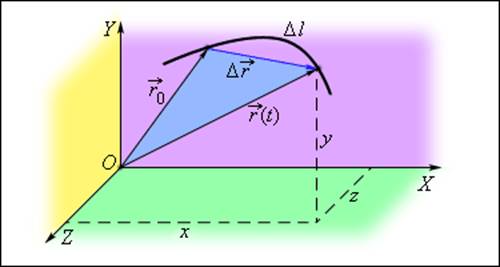
Рисунок 1.1.1.
Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t)
и радиус-вектора 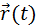
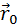 – радиус-вектор положения точки в начальный момент времени
– радиус-вектор положения точки в начальный момент времени
Перемещением тела
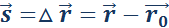
называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.
В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения 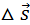 При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
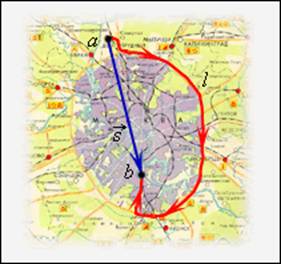
Рисунок 1.1.2.
Пройденный путь l и вектор перемещения 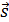 при криволинейном движении тела. a и b – начальная и конечная точки пути при криволинейном движении тела. a и b – начальная и конечная точки пути
|
Для характеристики движения вводится понятие средней скорости:
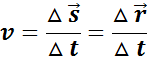
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt,
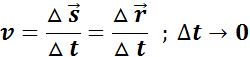
В математике такой предел называют производной и обозначают
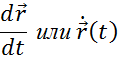
Мгновенная скорость 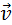 тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
|
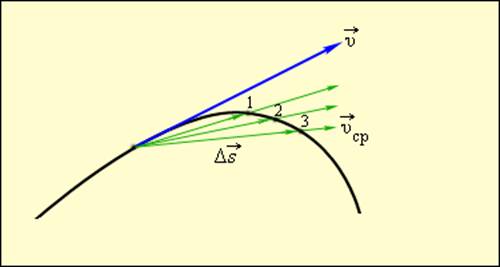
Рисунок 1.1.3.
Средняя и мгновенная скорости.
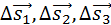 – перемещения за времена – перемещения за времена 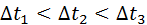 соответственно.
При t→0 соответственно.
При t→0
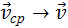
|
При движении тела по криволинейной траектории его скорость 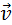 изменяется по модулю и направлению. Изменение вектора скорости
изменяется по модулю и направлению. Изменение вектора скорости 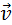 за некоторый малый промежуток времени Δt можно задать с помощью вектора
за некоторый малый промежуток времени Δt можно задать с помощью вектора 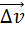 (рис. 1.1.4).
(рис. 1.1.4).
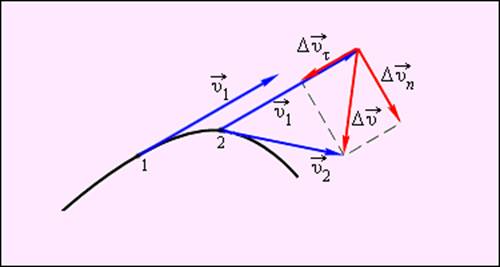
Вектор изменения скорости 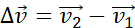 за малое время Δt можно разложить на две составляющие:
за малое время Δt можно разложить на две составляющие: 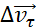 направленную вдоль вектора
направленную вдоль вектора 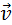 (касательная составляющая), и
(касательная составляющая), и 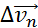 направленную перпендикулярно вектору
направленную перпендикулярно вектору 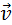 (нормальная составляющая).
(нормальная составляющая).
|
Рисунок 1.1.4.
Изменение вектора скорости по величине и направлению. 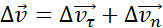 – изменение вектора скорости за время Δt – изменение вектора скорости за время Δt
|
Мгновенным ускорением (или просто ускорением) тела 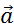 называют предел отношения малого изменения скорости
называют предел отношения малого изменения скорости 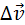 к малому промежутку времени Δt, в течение которого происходило изменение скорости:
к малому промежутку времени Δt, в течение которого происходило изменение скорости:
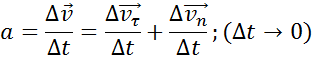
Направление вектора ускорения 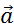 в случае криволинейного движения не совпадает с направле
в случае криволинейного движения не совпадает с направле 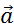 нием вектора
нием вектора 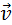 скорости Составляющие вектора ускорения называют касательным(тангенциальным)
скорости Составляющие вектора ускорения называют касательным(тангенциальным) 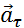 и нормальным
и нормальным 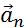 ускорениями (рис. 1.1.5).
ускорениями (рис. 1.1.5).
|
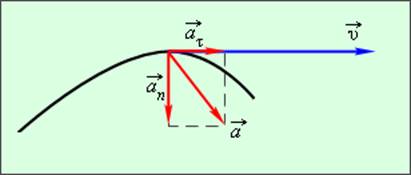
| Рисунок 1.1.5. Касательное и нормальное ускорения |
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:
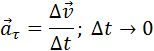
Вектор 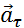 направлен по касательной к траектории.
направлен по касательной к траектории.
Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
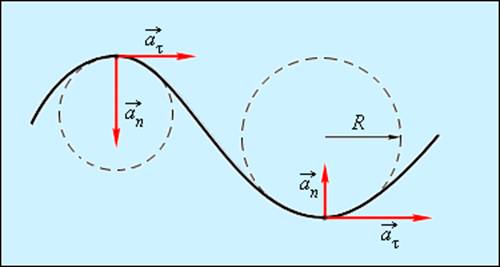
|
| Рисунок 1.1.6. Движение по дугам окружностей |
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент: 
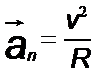
(Эта формула сделана в Mathtype)
Вектор 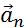 всегда направлен к центру окружности.
всегда направлен к центру окружности.
Из рис. 1.1.5 видно, что модуль полного ускорения равен
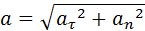
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение 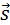 , скорость
, скорость 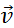 и ускорение
и ускорение 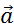 . Путь l является скалярной величиной. Перемещение
. Путь l является скалярной величиной. Перемещение 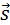 , скорость
, скорость 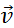 и ускорение
и ускорение 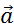 – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
– величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
2. Динамика
Основы динамики
Если в кинематике только описывается движение тел, то в динамике изучаются причины этого движения под действием сил, действующих на тело.
Динамика – раздел механики, который изучает взаимодействия тел, причины возникновения движения и тип возникающего движения. Взаимодействие – процесс, в ходе которого тела оказывают взаимное действие друг на друга. В физике все взаимодействия обязательно парные. Это значит, что тела взаимодействуют друг с другом парами. То есть всякое действие обязательно порождает противодействие.
Сила – это количественная мера интенсивности взаимодействия тел. Сила является причиной изменения скорости тела целиком или его частей (деформации). Сила является векторной величиной. Прямая, вдоль которой направлена сила, называется линией действия силы. Сила характеризуется тремя параметрами: точкой приложения, модулем (численным значением) и направлением. В Международной системе единиц (СИ) сила измеряется в Ньютонах (Н). Для измерения сил используют откалиброванные пружины. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра.
Сила, оказывающая на тело такое же действие, как и все силы, действующие на него, вместе взятые, называется равнодействующей силой. Она равна векторной сумма всех сил, действующих на тело:
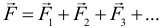
Чтобы найти векторную сумму нескольких сил нужно выполнить чертеж, где правильно нарисовать все силы и их векторную сумму, и по данному чертежу с использованием знаний из геометрии (в основном это теорема Пифагора и теорема косинусов) найти длину результирующего вектора.
Виды сил:
Сила тяжести. Приложена к центру масс тела и направлена вертикально вниз (или что тоже самое: перпендикулярно линии горизонта), и равна:
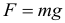
где: g - ускорение свободного падения, m - масса тела. Не перепутайте: сила тяжести перпендикулярна именно горизонту, а не поверхности на которой лежит тело. Таким образом, если тело лежит на наклонной поверхности, сила тяжести по-прежнему будет направлена строго вниз.
Сила трения. Приложена к поверхности соприкосновения тела с опорой и направлена по касательной к ней в сторону противоположную той, куда тянут, или пытаются тянуть тело другие силы.
Сила вязкого трения (сила сопротивления среды). Возникает при движении тела в жидкости или газе и направлена против скорости движения.
Сила реакции опоры. Действует на тело со стороны опоры и направлена перпендикулярно опоре от нее. Когда тело опирается на угол, то сила реакции опоры направлена перпендикулярно поверхности тела.
Сила натяжения нити. Направлена вдоль нити от тела.
Сила упругости. Возникает при деформации тела и направлена против деформации.
Обратите внимание и отметьте для себя очевидный факт: если тело находится в покое, то равнодействующая сил равна нулю.
Закон сохранения
Кинетическая энергия тела массой m, движущегося со скоростью  :
:
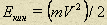 .
.
Потенциальная энергия тела массой m, находящегося на высоте h, в поле сил тяжести с ускорением свободного падения 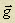 :
:
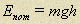 .
.
Энергия пружины с коэффициентом жесткости k, сжатой или растянутой на 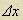 :
:
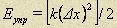 .
.
Импульс тела массой m, движущегося со скоростью  :
:
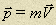 .
.
Закон сохранения энергии:
В замкнутых системах полная энергия (потенциальная + кинетическая + тепловая) системы тел сохраняется.
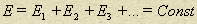 .
.
Если при этом можно пренебречь переходом механической энергии (потенциальная + кинетическая) в тепловую, то сохраняется механическая энергия системы.
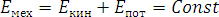
Абсолютно упругим ударом называется такое кратковременное взаимодействие тел, после которого тела полностью восстанавливают свою форму, а их суммарная кинетическая энергия не изменяется. При абсолютно упругом ударе выполняются закон сохранения импульса и закон сохранения механической энергии.
Абсолютно неупругим ударом называется такое кратковременное взаимодействие тел, после которого соударяющиеся тела образуют единое тело, движущееся с определенной скоростью, а суммарная кинетическая энергия тел уменьшается. При абсолютно неупругом ударе выполняется закон сохранения импульса, а механическая энергия не сохраняется, часть ее превращается во внутреннюю энергию тел.
Закон сохранения импульса:
Полный импульс замкнутой системы тел остается постоянным.
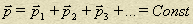 .
.
Работа постоянной силы 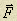 :
:
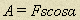 ,
,
где s – модуль перемещения, 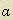 - угол между векторами силы
- угол между векторами силы 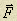 и перемещения
и перемещения  .
.
Работа так же может быть найдена по следующей формуле:
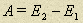 .
.
Мощность – работа A совершенная за единицу времени:
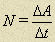 .
.
Силы:
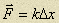 - сила упругости.
- сила упругости.
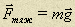 - сила тяжести.
- сила тяжести.
Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).
Первый закон Ньютона. Инерциальные и неинерциальные системы отсчёта Всякому телу свойственно сохранять состояние равномерного прямолинейного движения или покоя, пока и поскольку другие тела не вынудят его изменить это состояние. Указанное свойство тел называется инерцией, инертностью. Первый закон выполняется не во всех системах отсчета, а только в инерциальных. Так что, по существу, первый закон постулирует существование инерциальных систем отсчёта, то есть таких, где выполняется закон инерции. По этому закону, существует хотя бы одна инерциальная система отсчёта, а следовательно, их бесконечное число: любая система отсчёта, движущаяся относительно инерциальной с постоянной скоростью ( 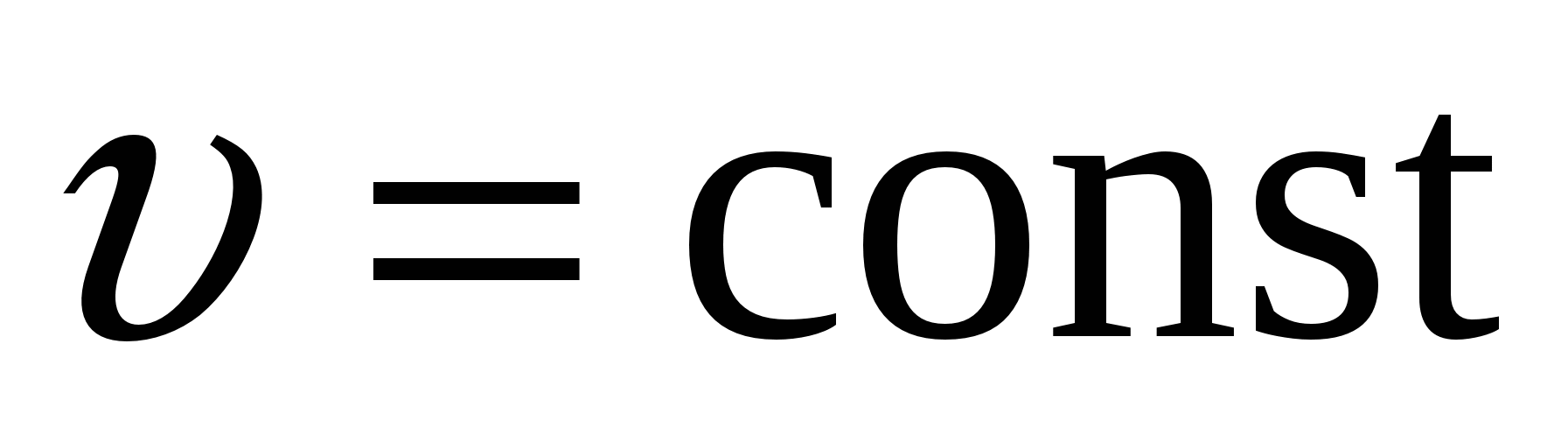 ), также является инерциальной. Неинерциальных систем отсчёта тоже бесконечно много: это – любая, движущаяся ускоренно относительно какой-либо инерциальной. 3. Второй закон Ньютона. Импульс тела, импульс силы В результате взаимодействия с другими телами тело может получить ускорение
), также является инерциальной. Неинерциальных систем отсчёта тоже бесконечно много: это – любая, движущаяся ускоренно относительно какой-либо инерциальной. 3. Второй закон Ньютона. Импульс тела, импульс силы В результате взаимодействия с другими телами тело может получить ускорение  . Одинаковое по величине воздействие разным телам сообщает разные ускорения: чем больше инертность тела, тем меньше ускорение. Количественной мерой инертности тела является масса
. Одинаковое по величине воздействие разным телам сообщает разные ускорения: чем больше инертность тела, тем меньше ускорение. Количественной мерой инертности тела является масса 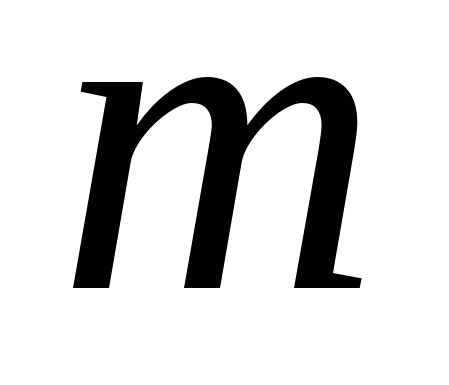 . Размерность массы в системе единиц СИ –
. Размерность массы в системе единиц СИ – 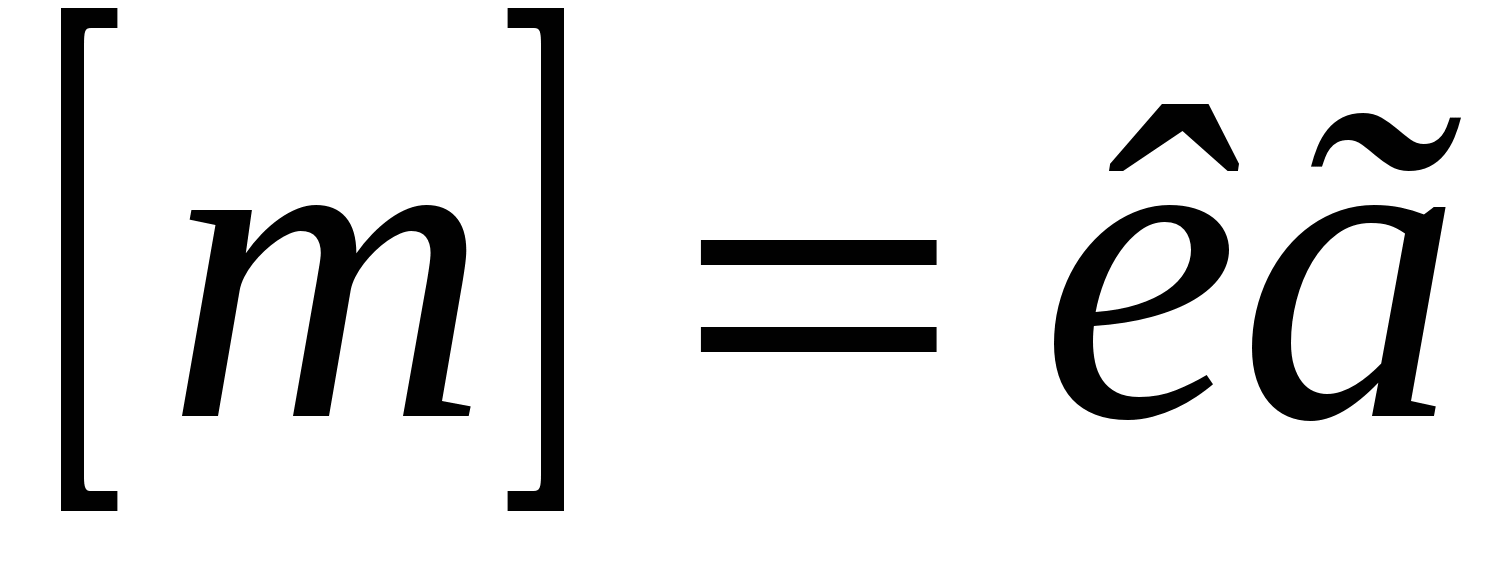 Сила – количественная мера воздействия одного тела на другое. Она характеризуется величиной, направлением и точкой приложения. Сила – вектор:
Сила – количественная мера воздействия одного тела на другое. Она характеризуется величиной, направлением и точкой приложения. Сила – вектор: 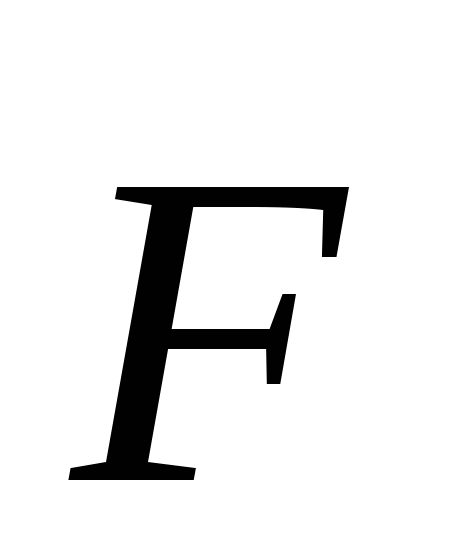 . Размерность силы – ньютон:
. Размерность силы – ньютон: 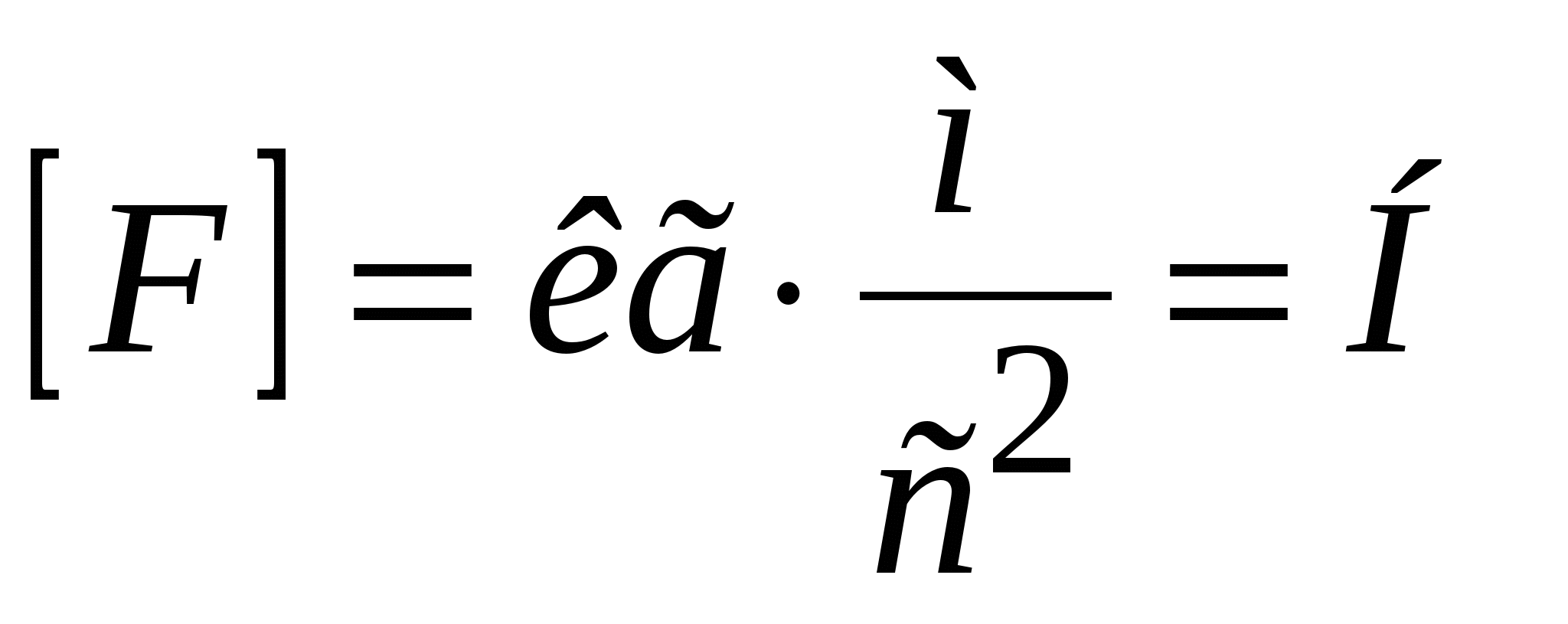 . Формулировка второго закона Ньютона: ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально массе тела
. Формулировка второго закона Ньютона: ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально массе тела 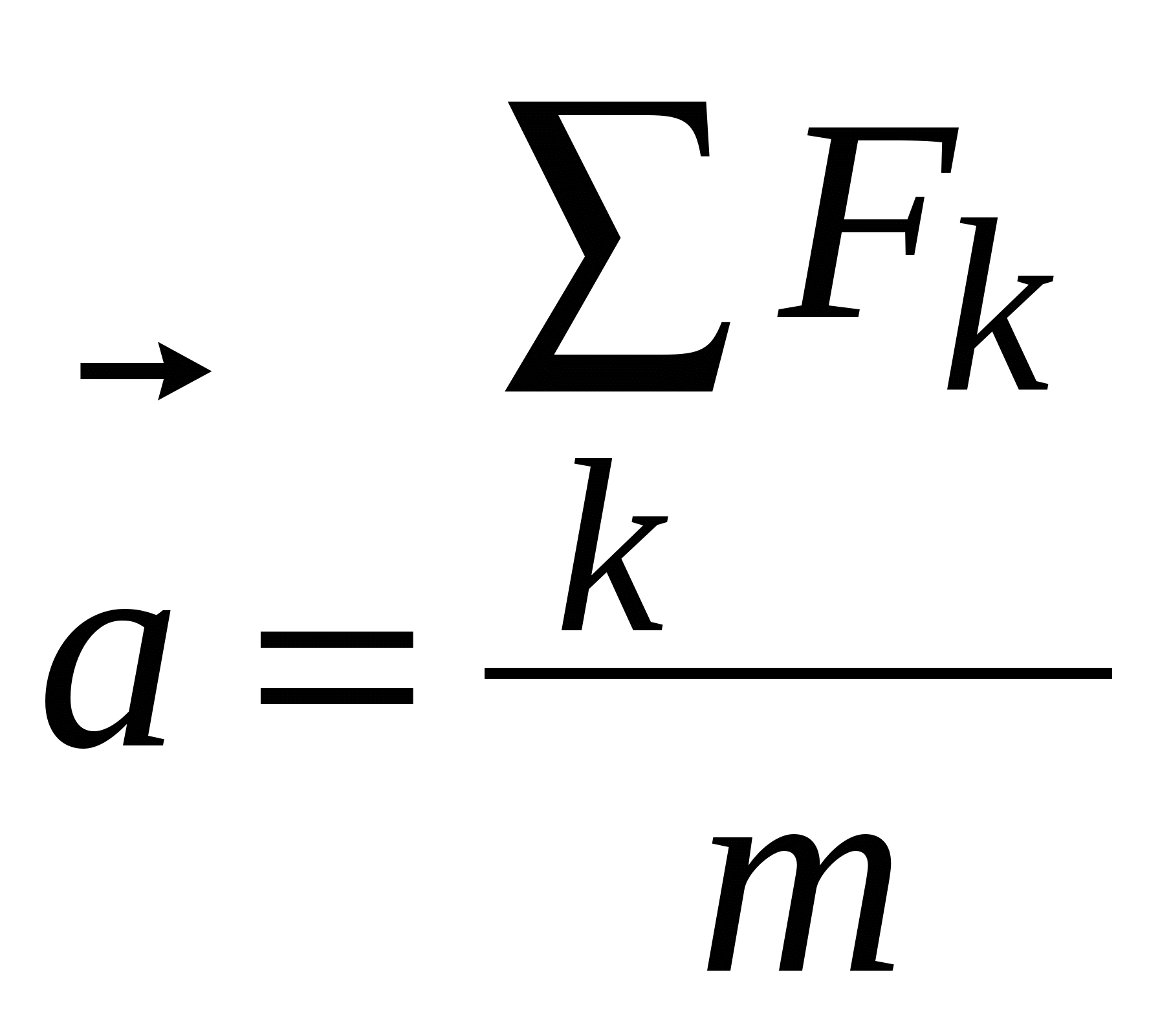 . (2.1) Напоминаем, что это – закон, полученный при обобщении опытных данных; он не доказывается. В числителе стоит равнодействующая всех сил, приложенных к телу, то есть их векторная сумма:
. (2.1) Напоминаем, что это – закон, полученный при обобщении опытных данных; он не доказывается. В числителе стоит равнодействующая всех сил, приложенных к телу, то есть их векторная сумма: 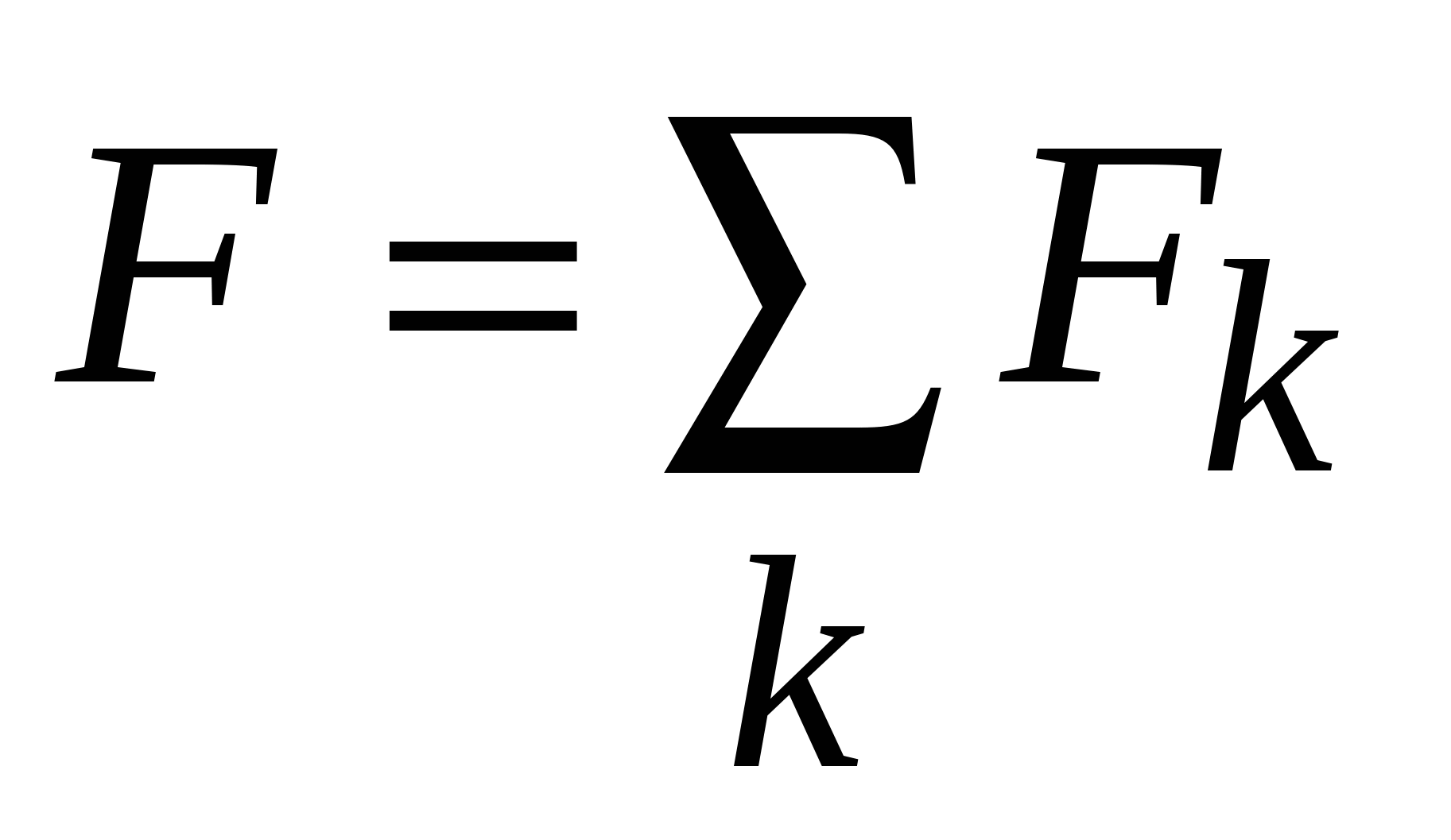 ; – её действие эквивалентно совместному действию всех реально приложенных к телу сил. По определению (см.лекцию 1) ускорение тела
; – её действие эквивалентно совместному действию всех реально приложенных к телу сил. По определению (см.лекцию 1) ускорение тела 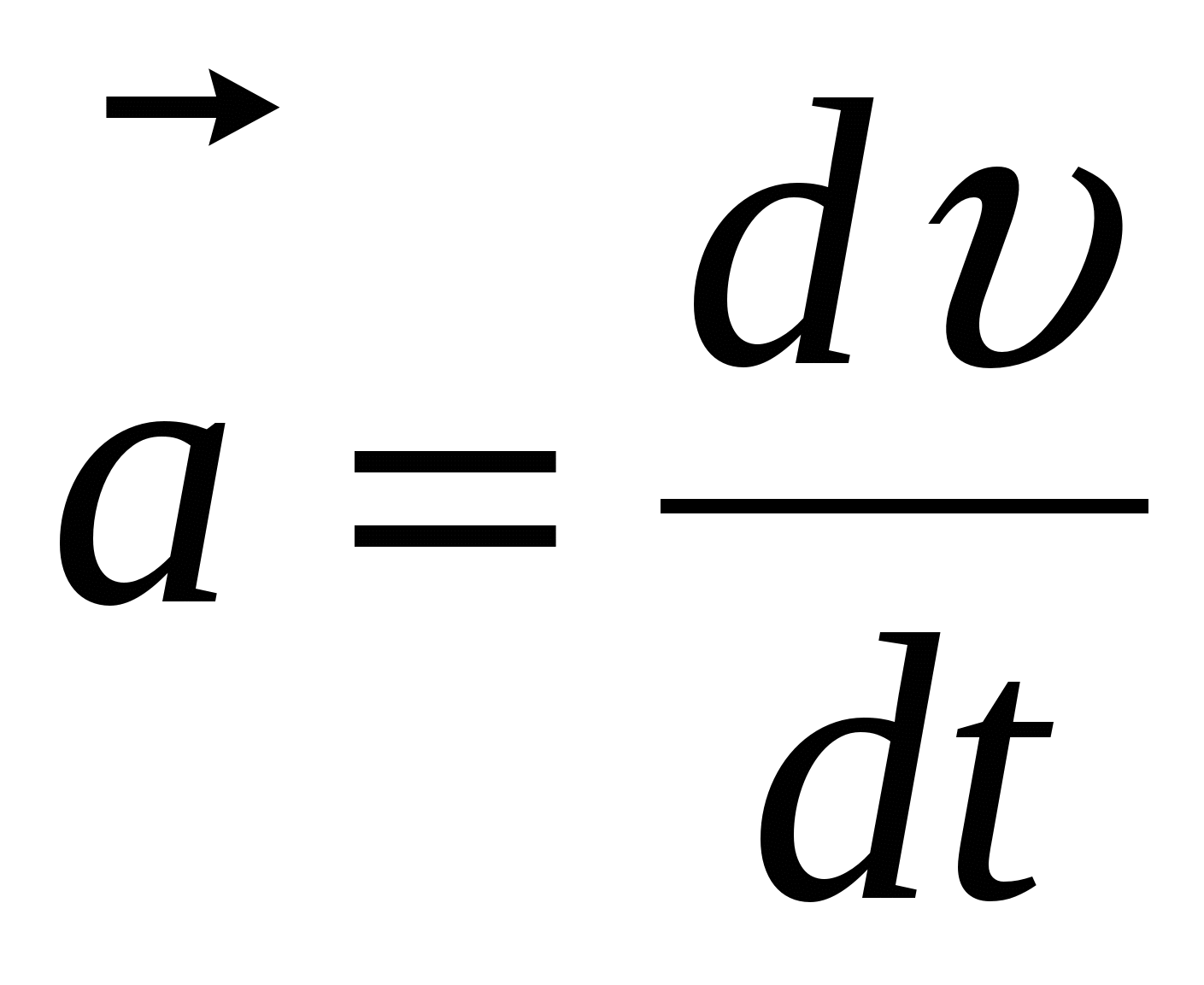 , тогда:
, тогда: 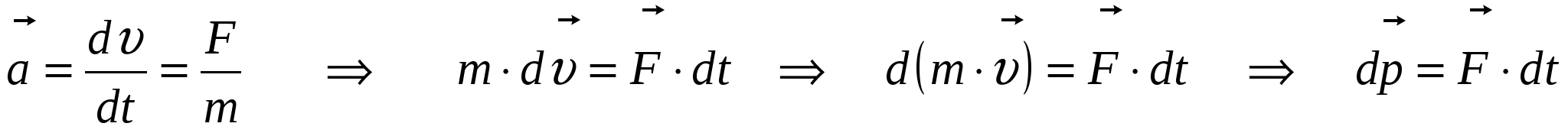 . Интегрируем последнее равенство:
. Интегрируем последнее равенство: 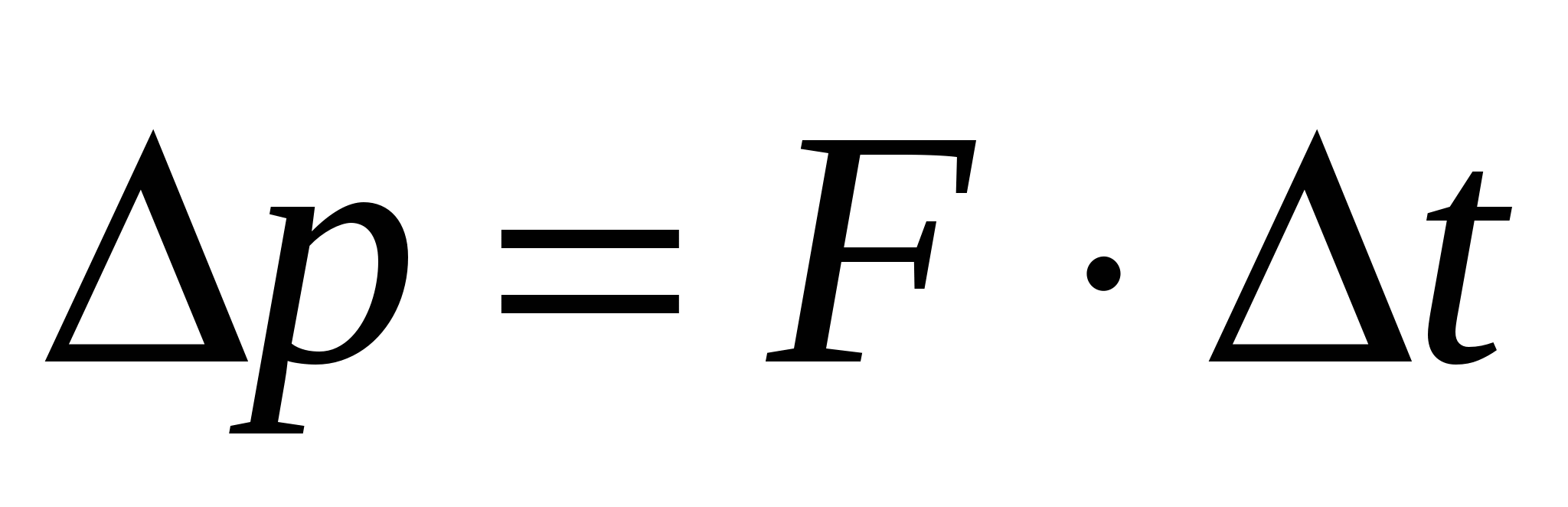 . (2.2) Это – второй закон Ньютона в импульсной форме: изменение импульса тела равно импульсу действовавшей на тело силы. Напоминаем, что произведение силы на промежуток времени, в течение которого она действовала, называется импульсом силы:
. (2.2) Это – второй закон Ньютона в импульсной форме: изменение импульса тела равно импульсу действовавшей на тело силы. Напоминаем, что произведение силы на промежуток времени, в течение которого она действовала, называется импульсом силы: 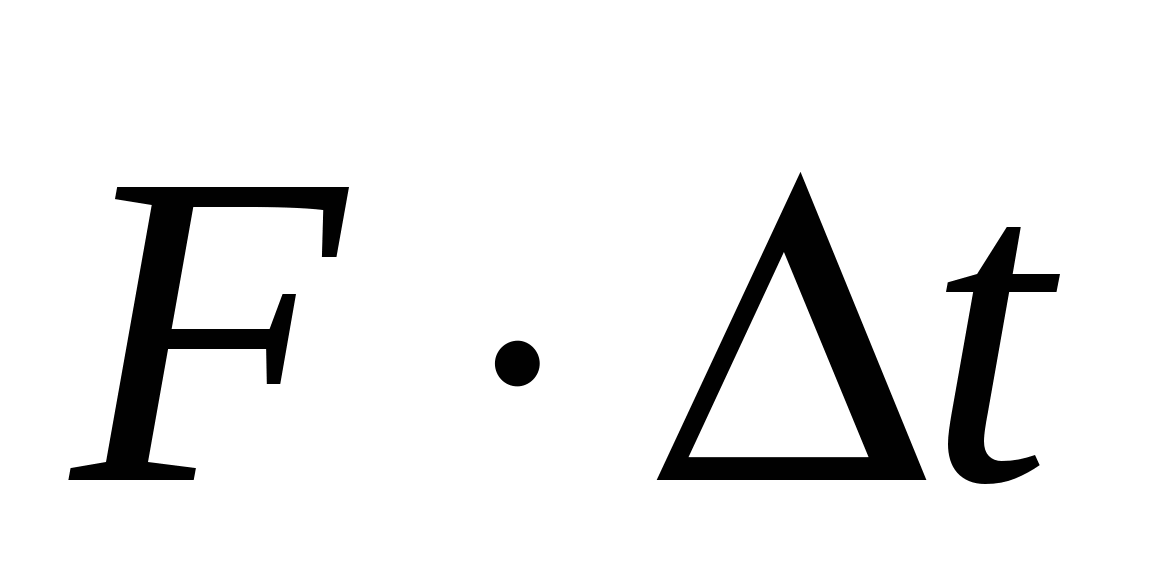 , (2.3) а произведение массы тела на его скорость – импульсом тела:
, (2.3) а произведение массы тела на его скорость – импульсом тела: 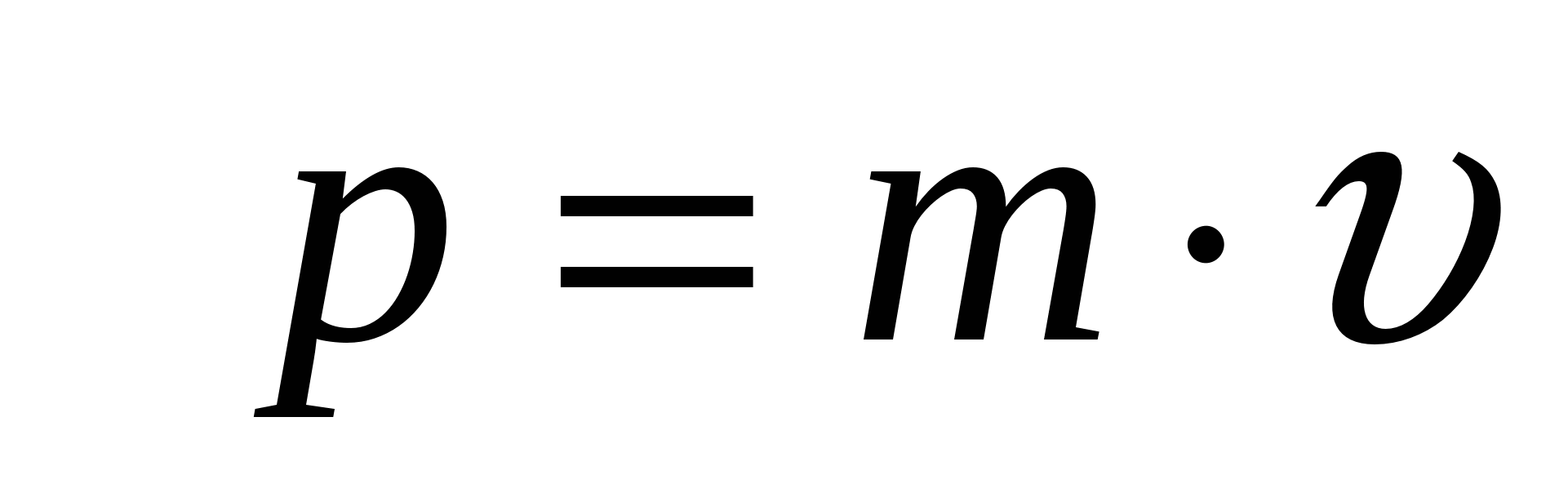 . (2.4) Второй закон Ньютона в виде (2.1) выполняется только при скоростях, много меньше скорости света; а в импульсной форме (2.5) его можно применять и при скоростях, сравнимых со скоростью света:
. (2.4) Второй закон Ньютона в виде (2.1) выполняется только при скоростях, много меньше скорости света; а в импульсной форме (2.5) его можно применять и при скоростях, сравнимых со скоростью света: 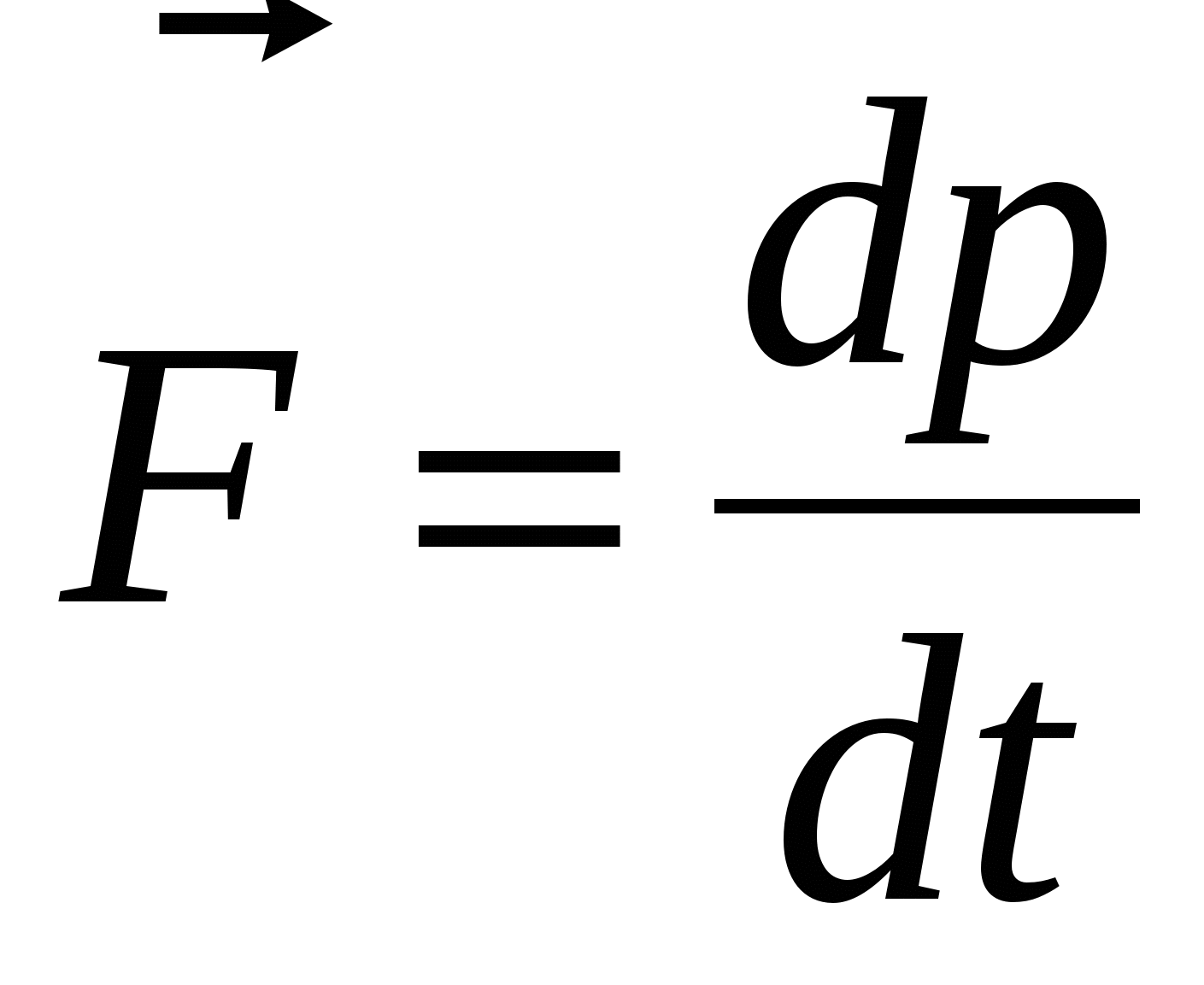 . (2.5) 4 . Третий закон Ньютона Всякое действие тел друг на друга носит характер взаимодействия. Тела действуют друг на друга с силами, равными по величине и направленными вдоль одной прямой в противоположные стороны. Из этого закона следует, что силы всегда появляются парами: если существует сила
. (2.5) 4 . Третий закон Ньютона Всякое действие тел друг на друга носит характер взаимодействия. Тела действуют друг на друга с силами, равными по величине и направленными вдоль одной прямой в противоположные стороны. Из этого закона следует, что силы всегда появляются парами: если существует сила 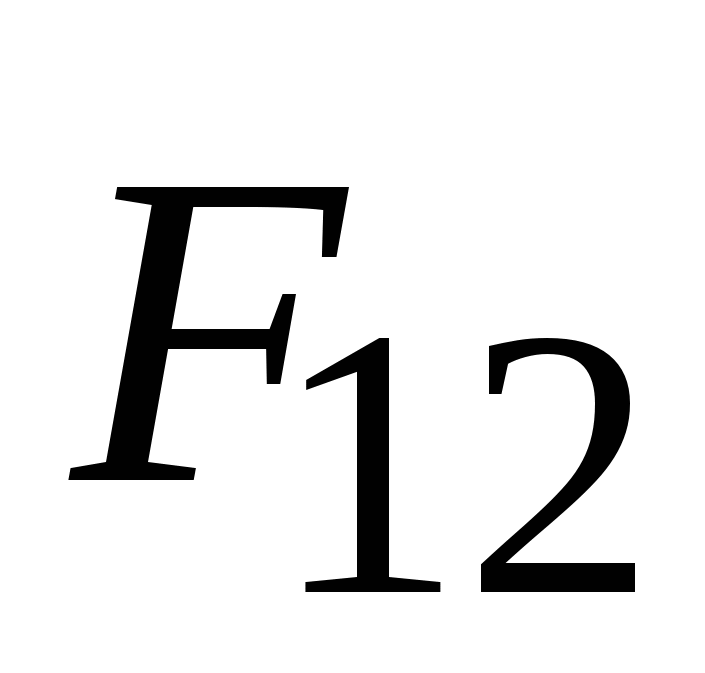 , действующая на тело 1 со стороны тела 2, что и тело 1 действует на тело 2 с силой
, действующая на тело 1 со стороны тела 2, что и тело 1 действует на тело 2 с силой 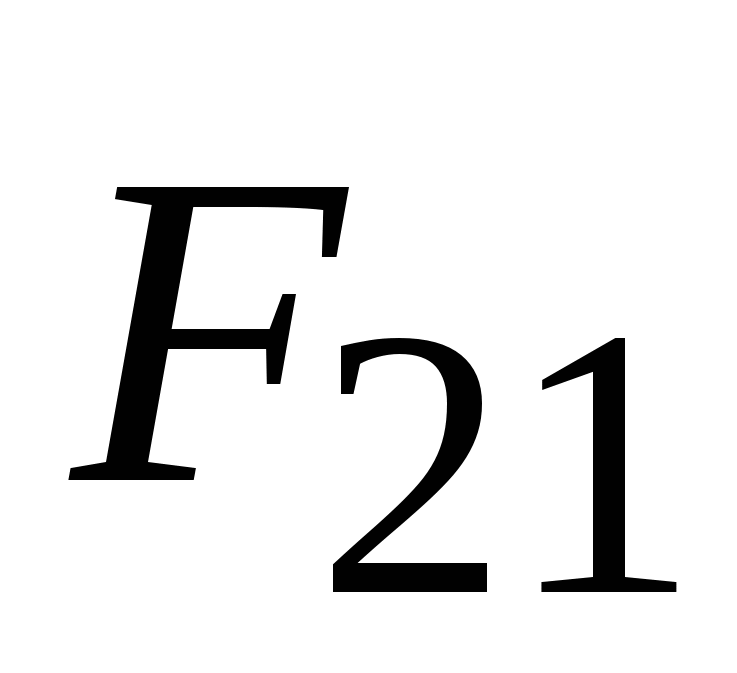 , равной по величине и противоположной по направлению:
, равной по величине и противоположной по направлению: 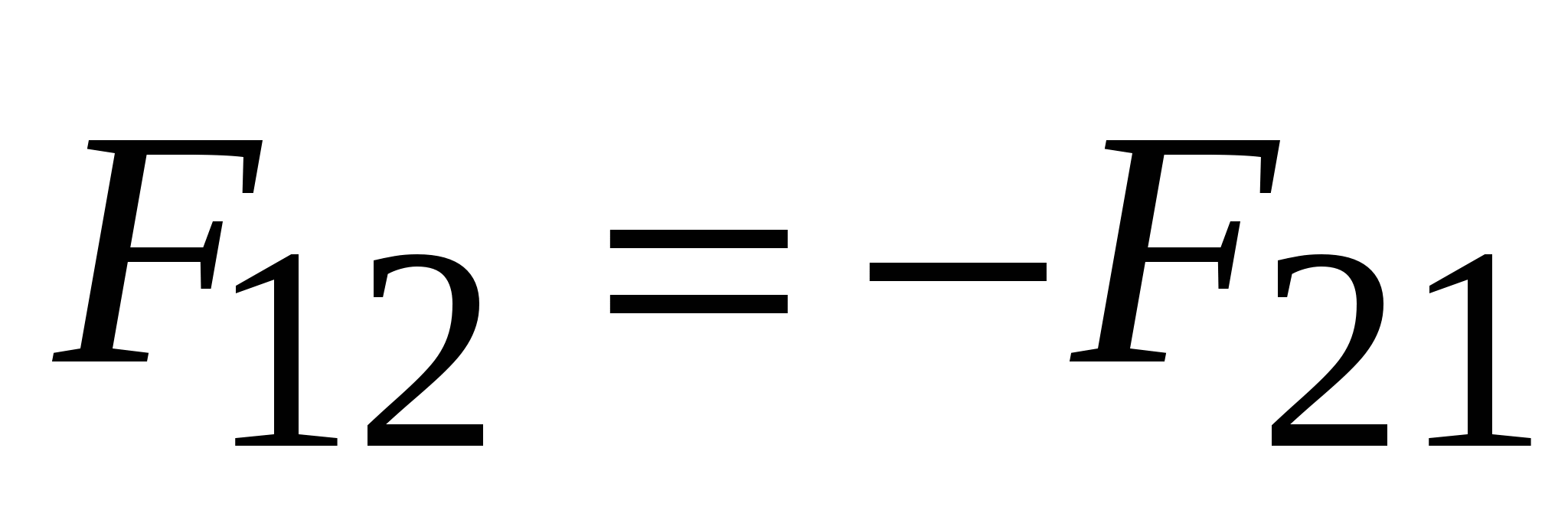 . (2.6) Природа этих сил одинакова. Эти силы не могут компенсировать друг друга, так как приложены к разным телам. В заключение рассмотрения законов Ньютона нужно подчеркнуть, что первый закон Ньютона устанавливает (постулирует) существование инерциальных систем отсчёта, а второй и третий законы Ньютона выполняются именно в таких (инерциальных) системах отсчёта. Сила всемирного тяготения. Закон всемирного тяготения. Сила тяжести, вес тела. Две материальные точки притягиваются друг к другу с силой, прямо пропорциональной каждой массе и обратно пропорциональной квадрату расстояния между точками:
. (2.6) Природа этих сил одинакова. Эти силы не могут компенсировать друг друга, так как приложены к разным телам. В заключение рассмотрения законов Ньютона нужно подчеркнуть, что первый закон Ньютона устанавливает (постулирует) существование инерциальных систем отсчёта, а второй и третий законы Ньютона выполняются именно в таких (инерциальных) системах отсчёта. Сила всемирного тяготения. Закон всемирного тяготения. Сила тяжести, вес тела. Две материальные точки притягиваются друг к другу с силой, прямо пропорциональной каждой массе и обратно пропорциональной квадрату расстояния между точками: 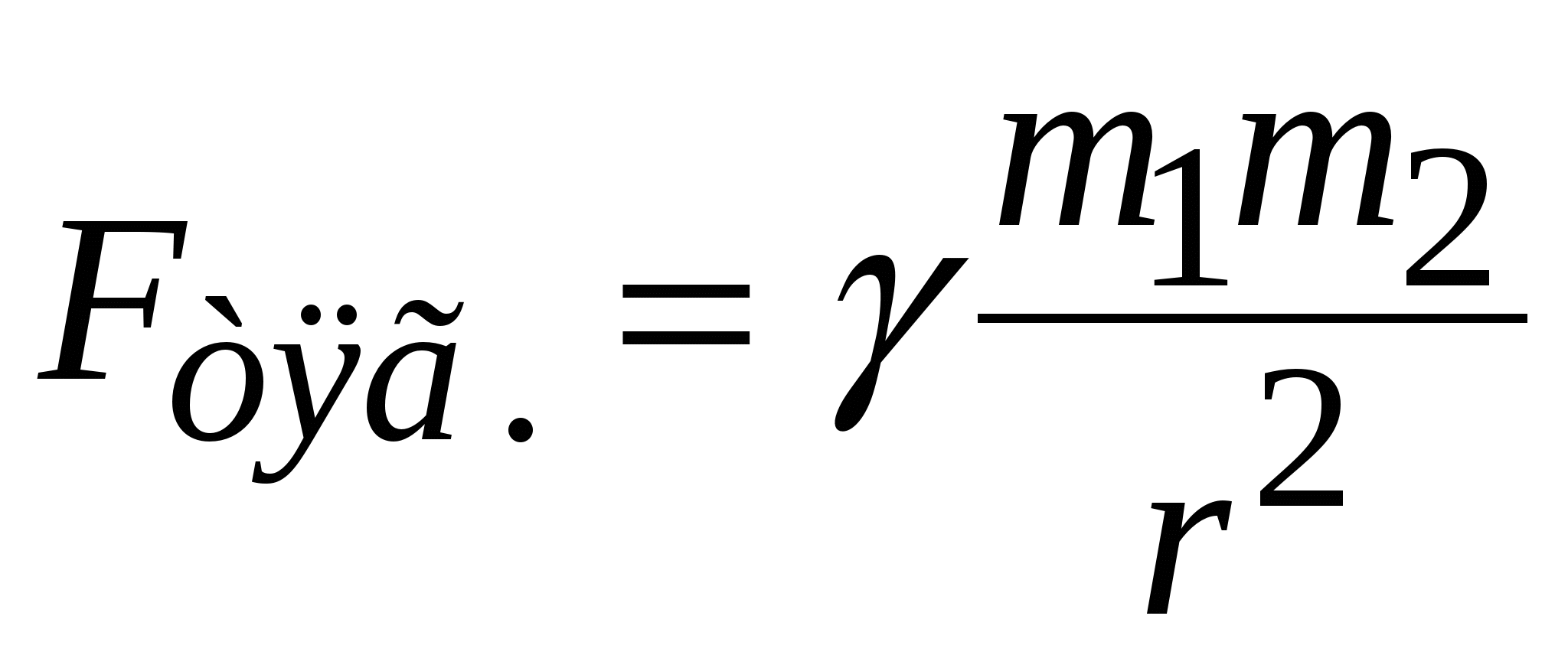 , (2.7) где
, (2.7) где 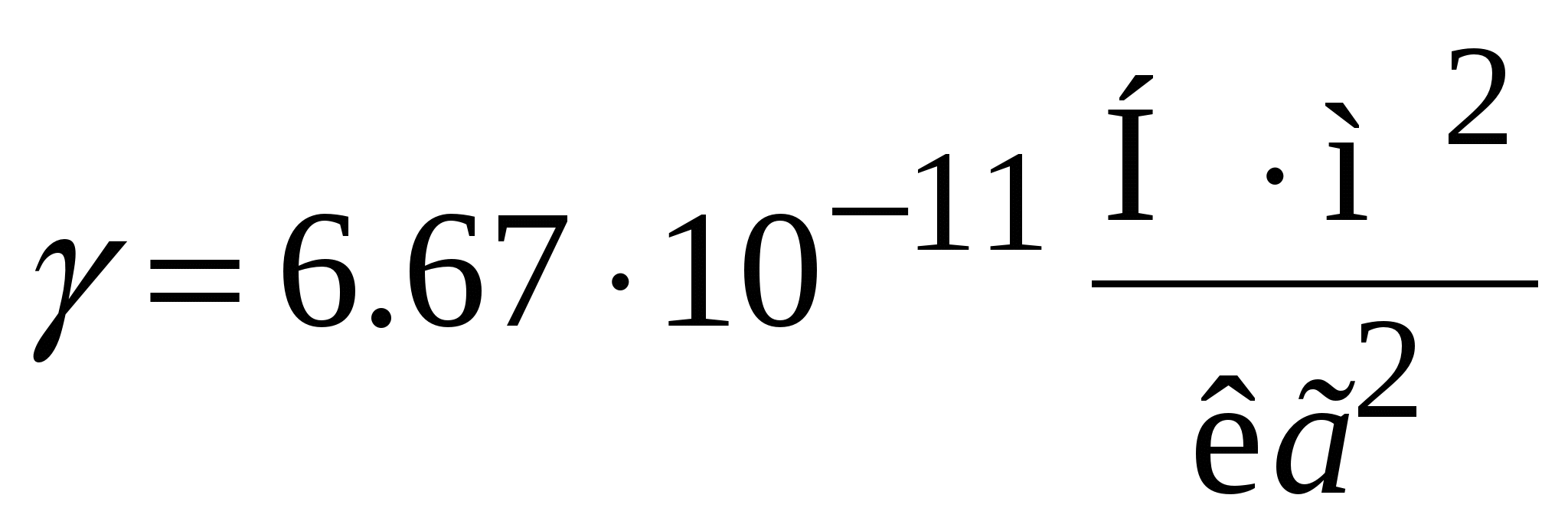 – гравитационная постоянная. Любая масса создаёт в окружающем пространстве гравитационное поле. Поле – это пространство с особым свойством: если в гравитационное поле поместить другую массу, то на неё со стороны поля будет действовать сила. Две массы взаимодействуют посредством гравитационного поля. Для гравитационных полей, как и для любых полей, характерно близкодействие, то есть гравитационное взаимодействие распространяется с конечной скоростью, равной скорости света в вакууме
– гравитационная постоянная. Любая масса создаёт в окружающем пространстве гравитационное поле. Поле – это пространство с особым свойством: если в гравитационное поле поместить другую массу, то на неё со стороны поля будет действовать сила. Две массы взаимодействуют посредством гравитационного поля. Для гравитационных полей, как и для любых полей, характерно близкодействие, то есть гравитационное взаимодействие распространяется с конечной скоростью, равной скорости света в вакууме 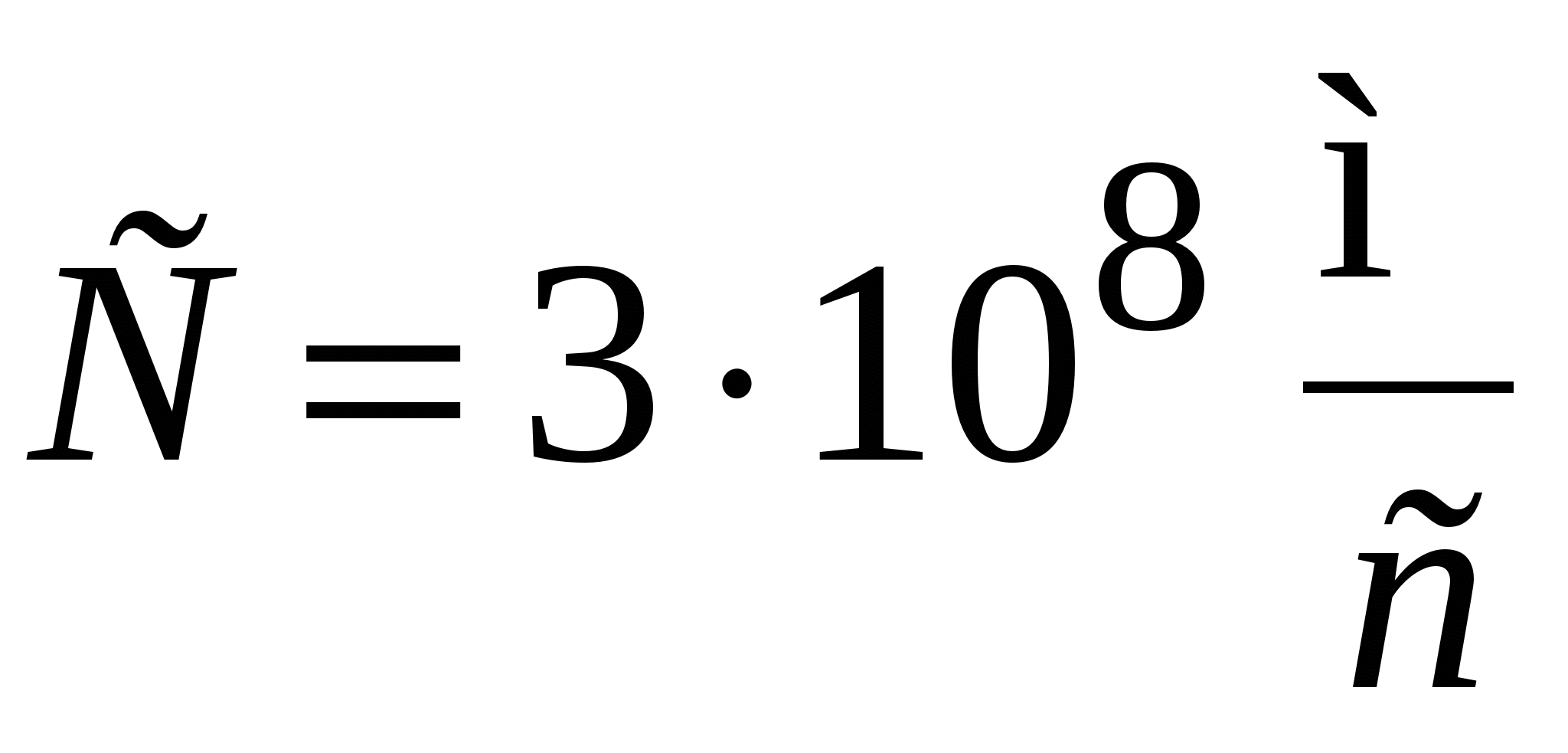 . Вблизи Земли (или другого небесного тела) с массой M, радиусом R тело массой m притягивается к ней с силой:
. Вблизи Земли (или другого небесного тела) с массой M, радиусом R тело массой m притягивается к ней с силой: 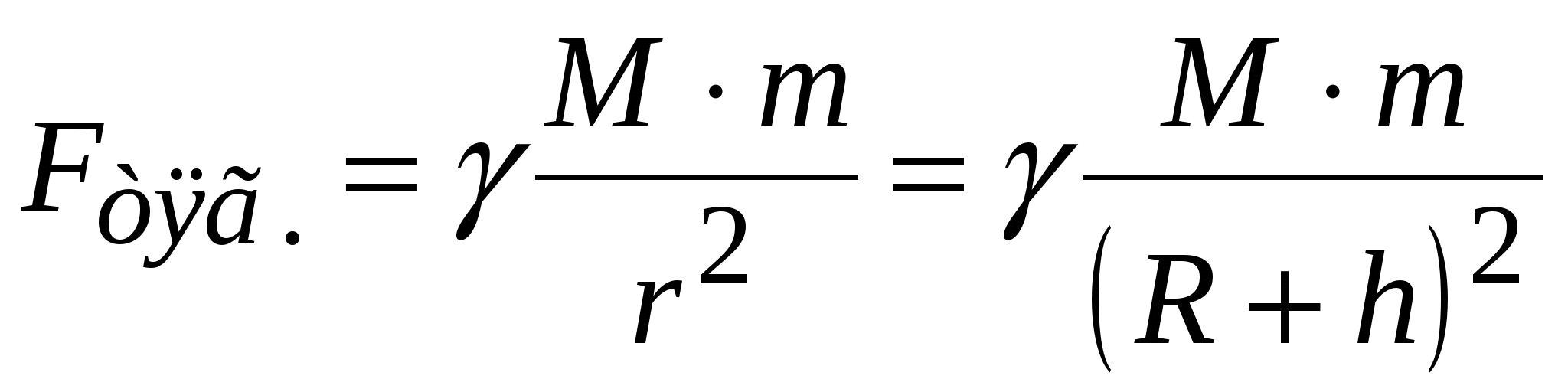 , (2.8) где
, (2.8) где 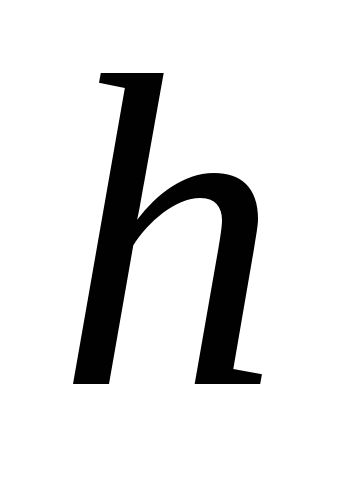 – высота над поверхностью Земли. Это – сила тяжести:
– высота над поверхностью Земли. Это – сила тяжести: 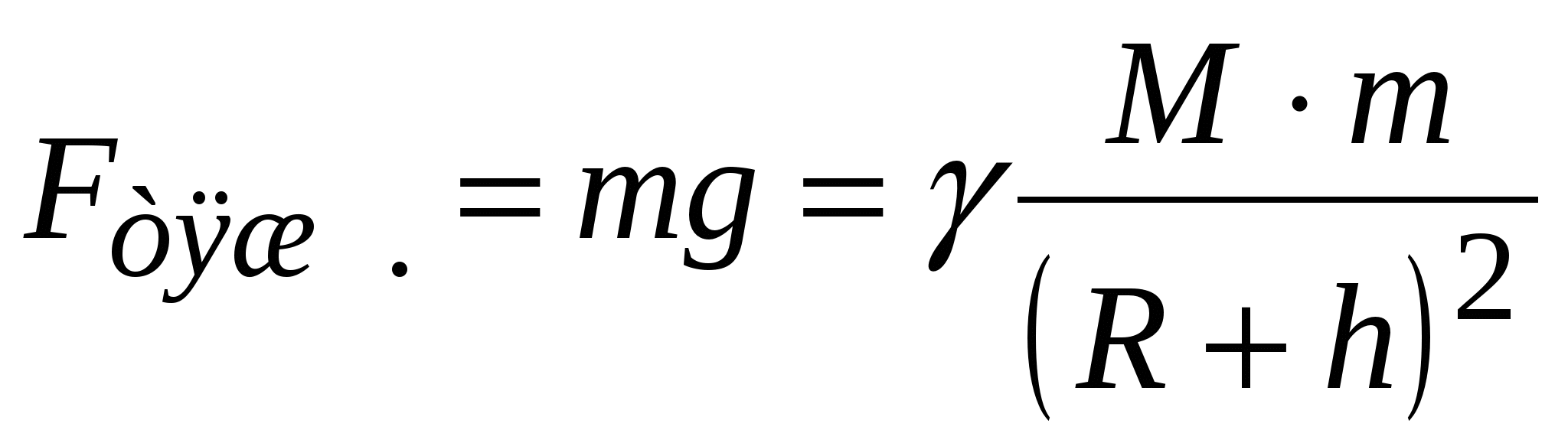 . (2.9) Величина ускорения свободного падения
. (2.9) Величина ускорения свободного падения 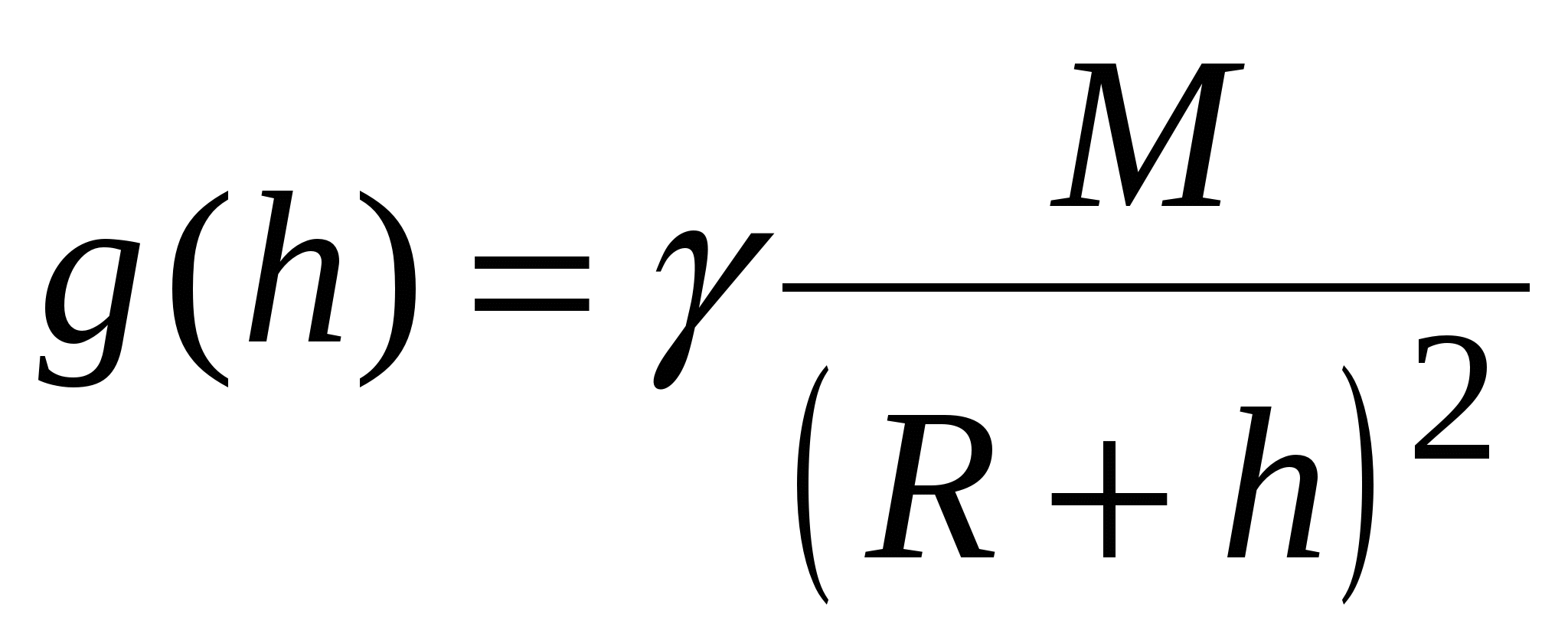 , а на поверхности Земли
, а на поверхности Земли 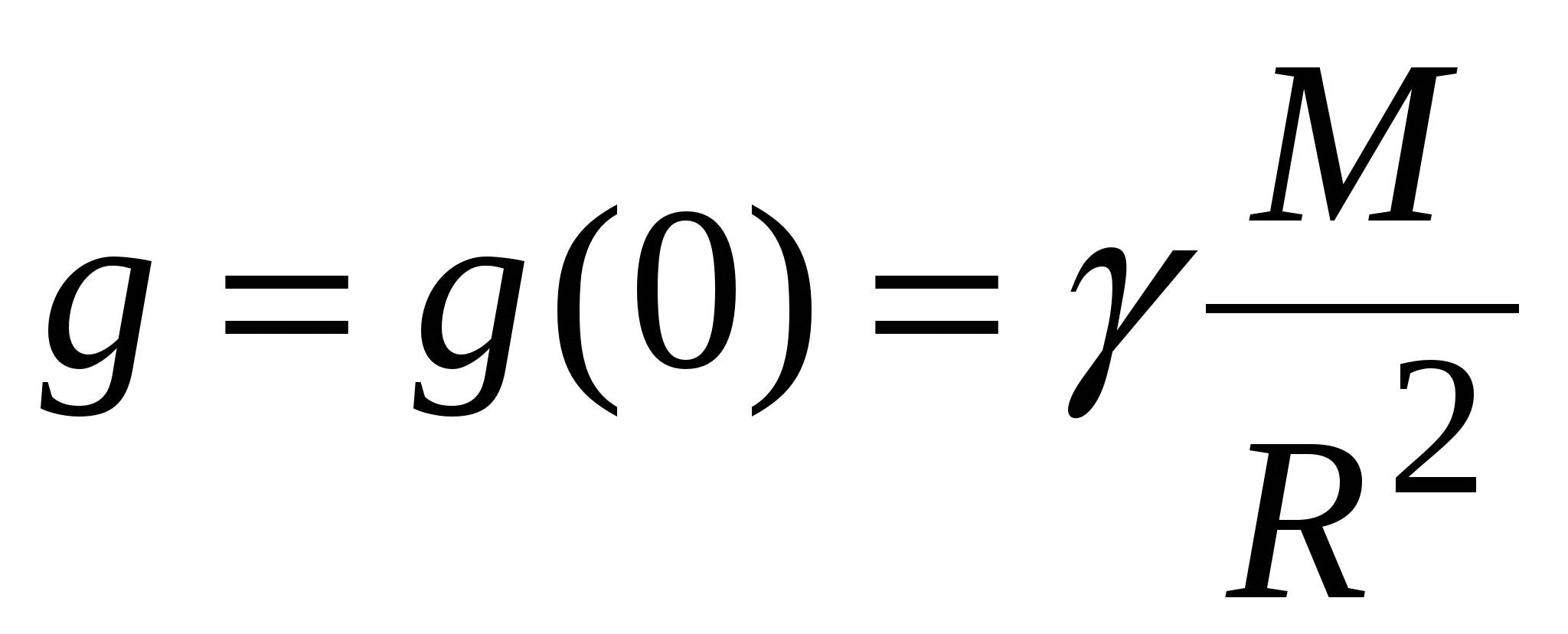 . (2.10) Вес тела
. (2.10) Вес тела 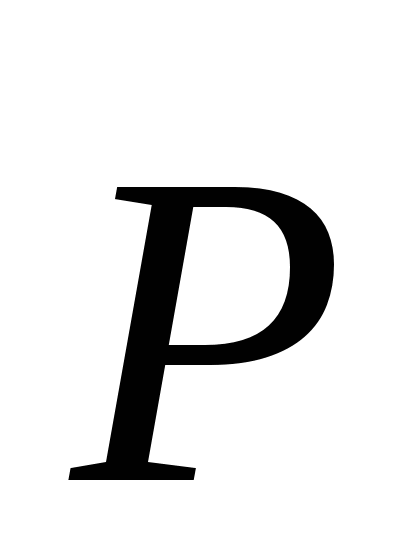 – это сила, с которой тело давит на подставку или растягивает подвес. Вес – сила, приложенная к подставке. Вес по третьему закону Ньютона равен и противоположен силе нормального давления
– это сила, с которой тело давит на подставку или растягивает подвес. Вес – сила, приложенная к подставке. Вес по третьему закону Ньютона равен и противоположен силе нормального давления  (или натяжения нити):
(или натяжения нити): 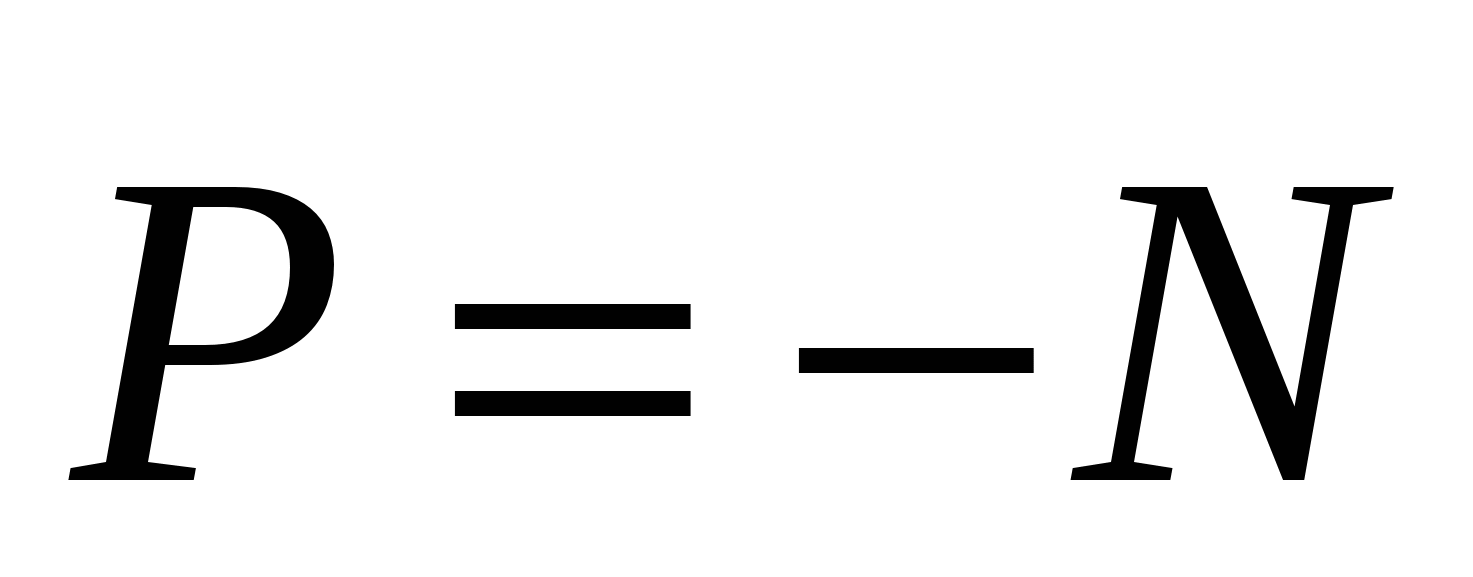 . Если тело неподвижно висит или лежит (или вместе с подставкой движется равномерно, – система отсчёта инерциальна), то по второму закону Ньютона, сумма сил, действующих на тело, то есть тяжести и нормального давления, будет равна нулю (ускорение отсутствует):
. Если тело неподвижно висит или лежит (или вместе с подставкой движется равномерно, – система отсчёта инерциальна), то по второму закону Ньютона, сумма сил, действующих на тело, то есть тяжести и нормального давления, будет равна нулю (ускорение отсутствует): 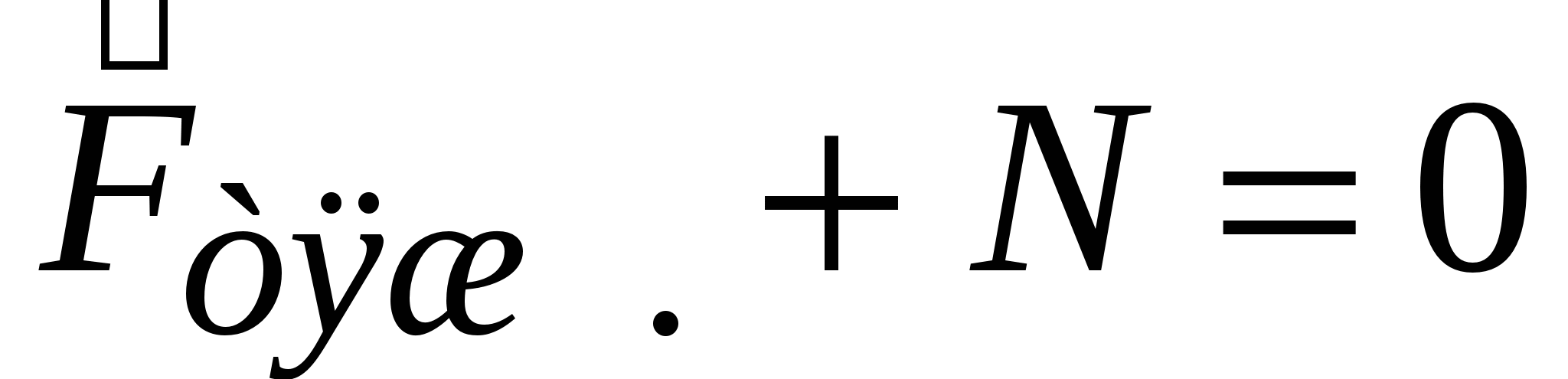 . Тогда вес
. Тогда вес 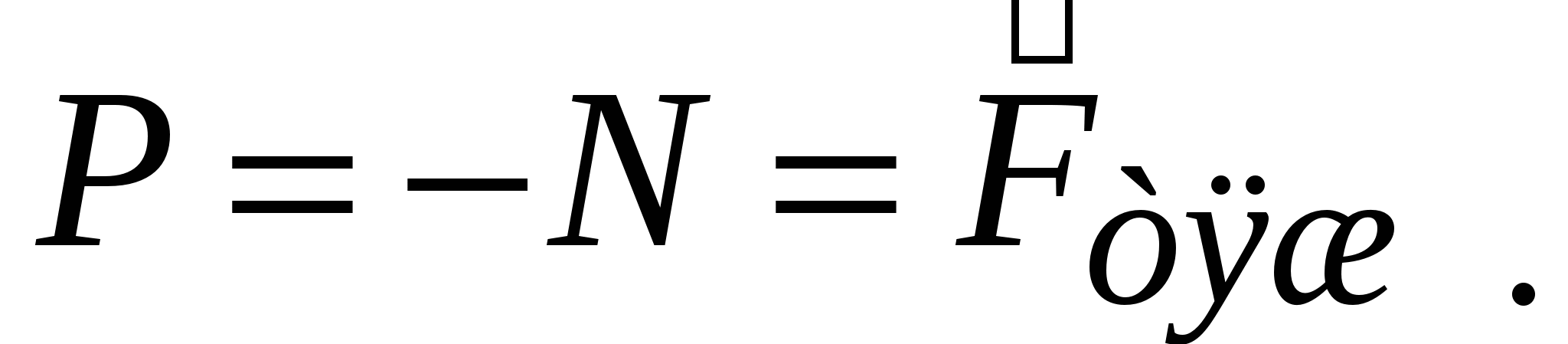 . Если тело движется ускоренно (
. Если тело движется ускоренно ( 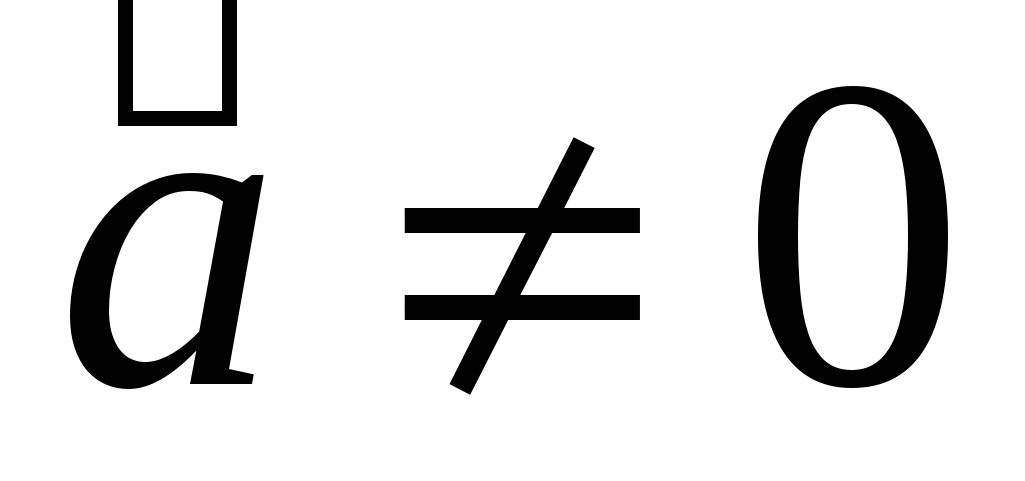 ) вместе с подставкой, то уравнение движения примет вид
) вместе с подставкой, то уравнение движения примет вид 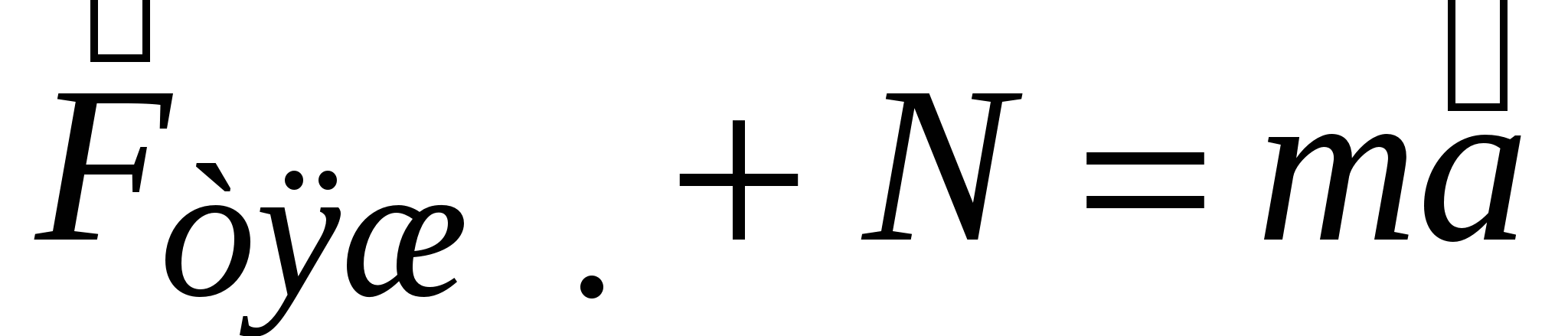 , и вес
, и вес 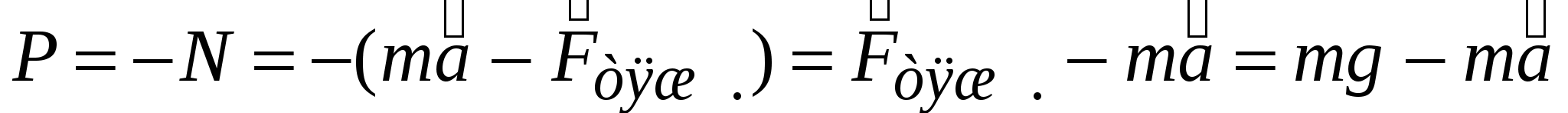 . Если, например, тело вместе с лифтом движется ускоренно вверх (рис.2.2), то в проекциях на ось OY
. Если, например, тело вместе с лифтом движется ускоренно вверх (рис.2.2), то в проекциях на ось OY 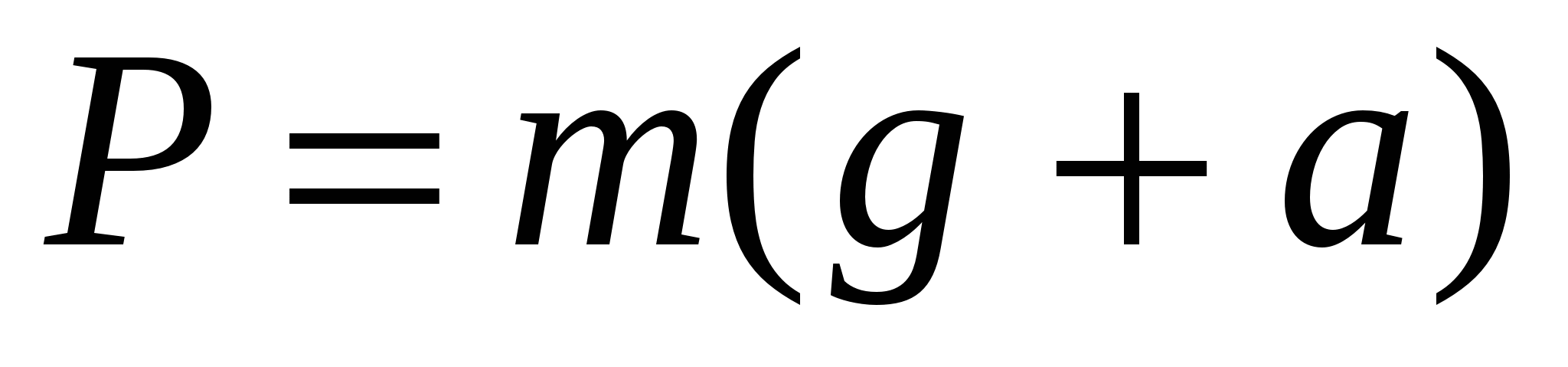 . (2.11) Если ускорение направлено вниз, то вес
. (2.11) Если ускорение направлено вниз, то вес 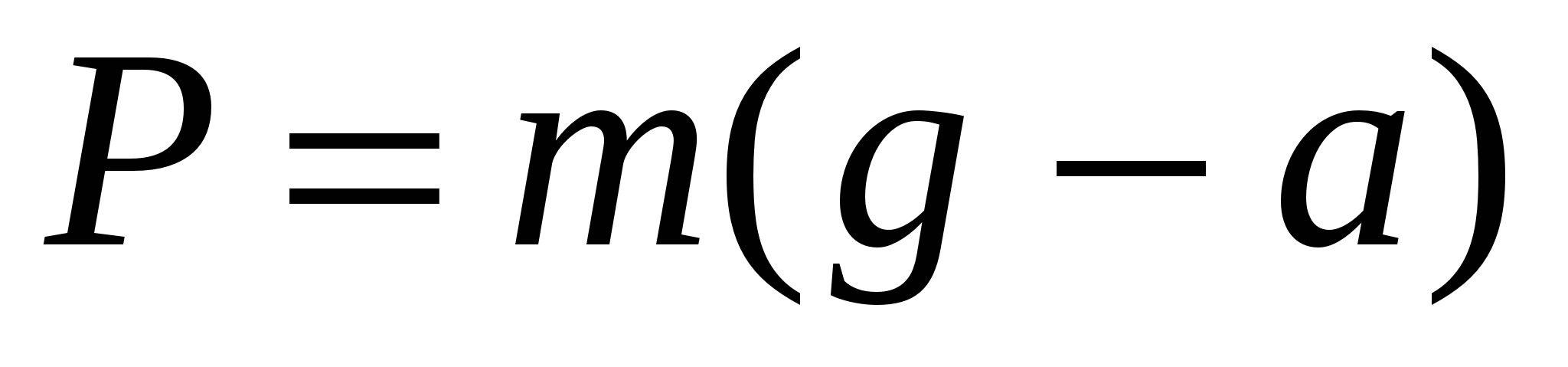 . (2.12) При
. (2.12) При 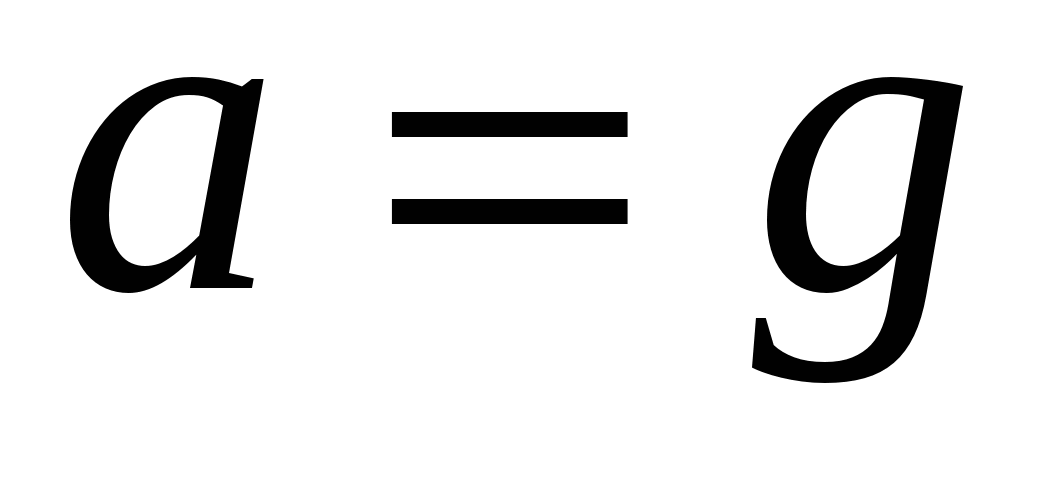 наступает невесомость:
наступает невесомость: 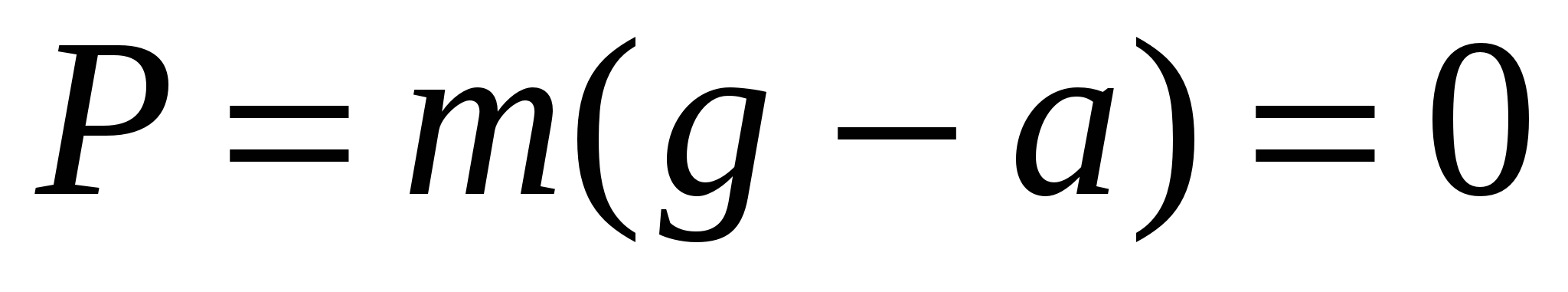 .
. 
Сила трения. Сила трения возникает при относительном перемещении соприкасающихся тел (или частей одного тела).
| Трение | |||||
| Сухое | Вязкое | ||||
| Покоя | Скольжения | Качения | |||
Будем рассматривать только сухое трение покоя и скольжения. Сила трения скольжения зависит от того, с какой силой прижаты тела друг к другу (от силы нормального давления  ):
): 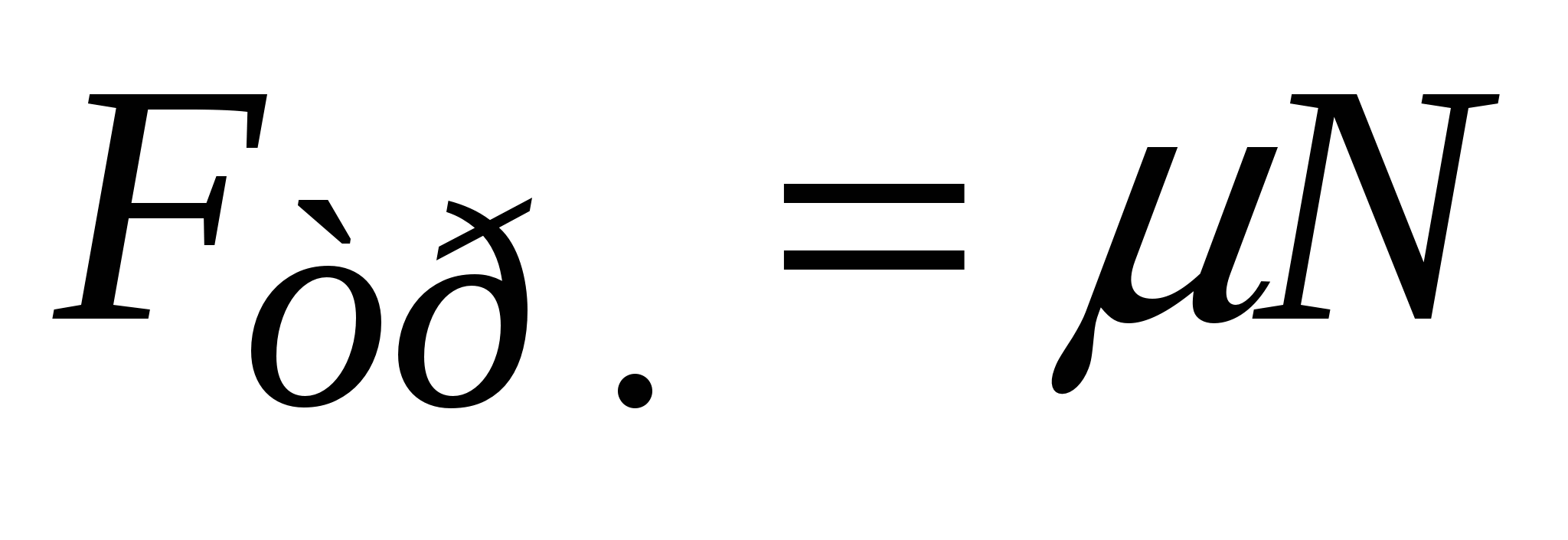 . (2.13) Здесь
. (2.13) Здесь  – коэффициент трения; он безразмерен; его величина не может быть больше единицы. Считаем, что в первом приближении сила трения скольжения не зависит от скорости. Сила трения покоя возникает при попытках переместить соприкасающиеся тела относительно друг друга (рис.2.3). Она может принимать любые значения от 0 до
– коэффициент трения; он безразмерен; его величина не может быть больше единицы. Считаем, что в первом приближении сила трения скольжения не зависит от скорости. Сила трения покоя возникает при попытках переместить соприкасающиеся тела относительно друг друга (рис.2.3). Она может принимать любые значения от 0 до  :
: 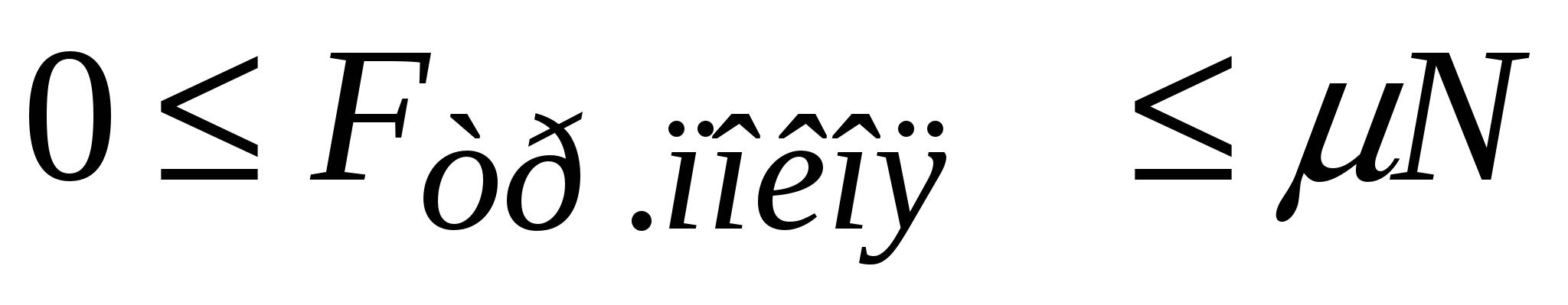 . Пока тело не сдвинулось, внешняя сила и сила трения покоя уравновешивают друг друга; с увеличением
. Пока тело не сдвинулось, внешняя сила и сила трения покоя уравновешивают друг друга; с увеличением  растёт и
растёт и 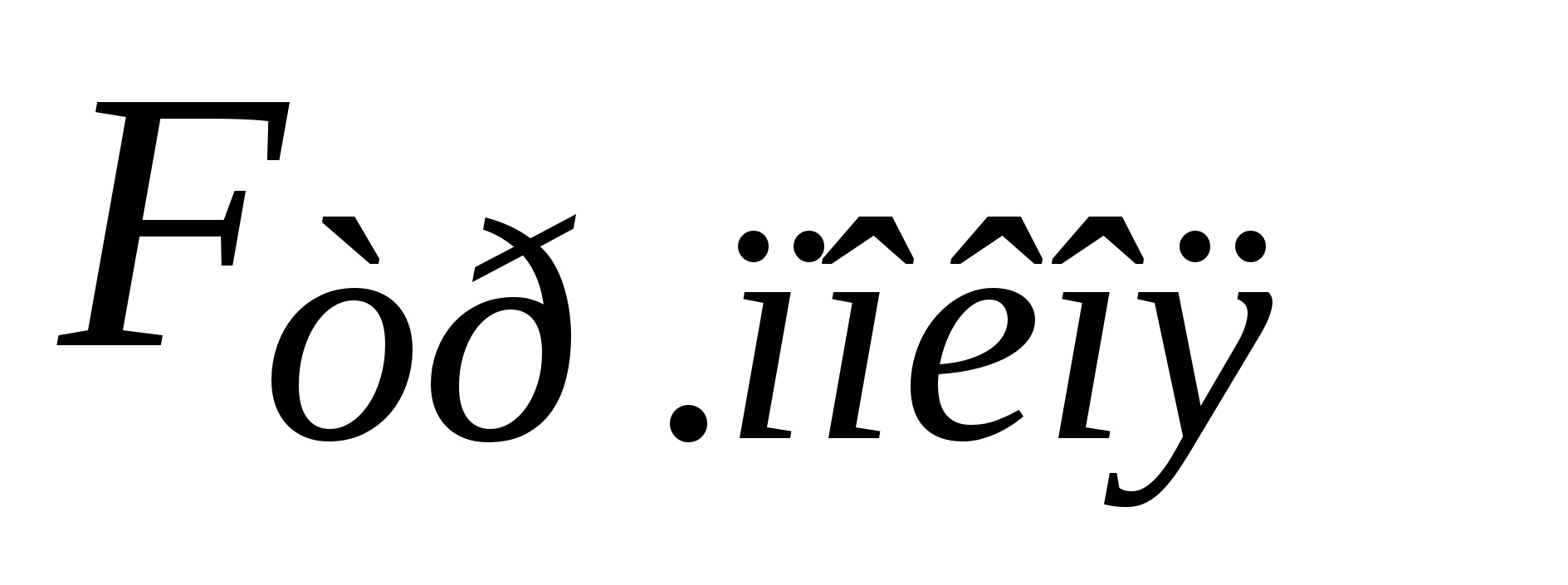 (участок 1 на рис.2.43):
(участок 1 на рис.2.43): 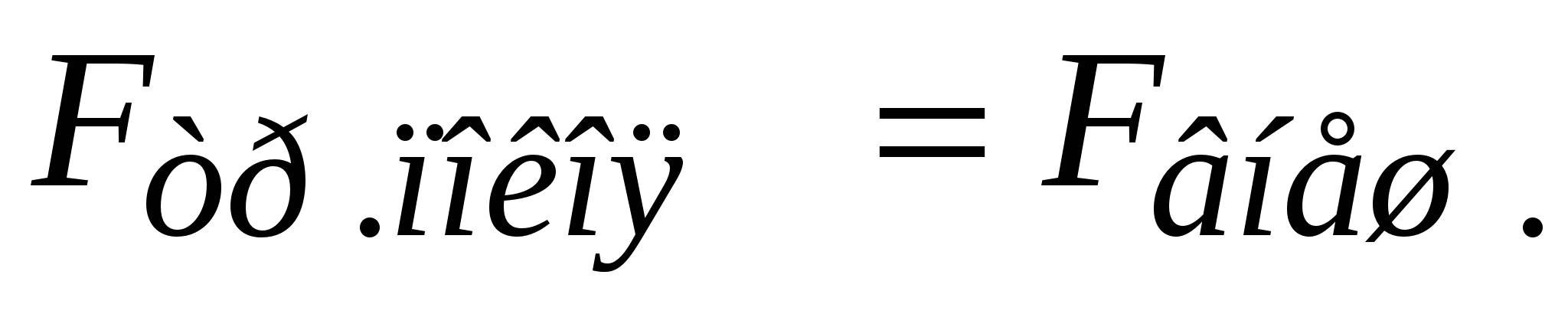 . Если внешняя сила превышает максимально возможное значение силы трения покоя, равное
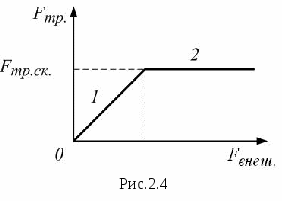
. Если внешняя сила превышает максимально возможное значение силы трения покоя, равное  , то тело сдвинется, и сила трения покоя перейдёт в силу трения скольжения (участок 2 на рис.2.4). Сила трения направлена по касательной с соприкасающимся поверхностям (рис.2.3). Причины возникновения сил трения – неровности, шероховатости поверхностей тел: при относительном перемещении неровности зацепляются, ломаются; при этом тратится энергия – тела нагреваются. Ещё одна причина – межмолекулярное (межатомное) взаимодействие: при соприкосновении частицы двух тел притягиваются. В конечном итоге трение – проявление электромагнитного взаимодействия.
, то тело сдвинется, и сила трения покоя перейдёт в силу трения скольжения (участок 2 на рис.2.4). Сила трения направлена по касательной с соприкасающимся поверхностям (рис.2.3). Причины возникновения сил трения – неровности, шероховатости поверхностей тел: при относительном перемещении неровности зацепляются, ломаются; при этом тратится энергия – тела нагреваются. Ещё одна причина – межмолекулярное (межатомное) взаимодействие: при соприкосновении частицы двух тел притягиваются. В конечном итоге трение – проявление электромагнитного взаимодействия. 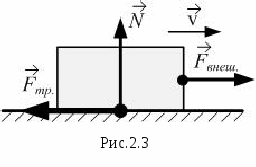
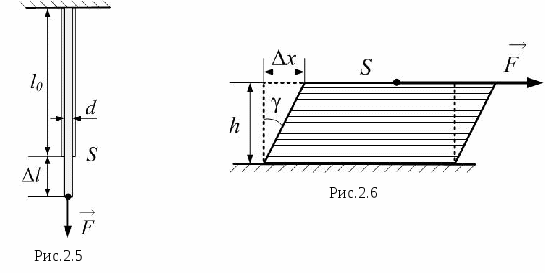
Силы упругости Причины возникновения сил упругости – также межмолекулярные (межатомные) взаимодействия и сводятся к электромагнитным силам: при изменении длины тела (например, при растяжении) увеличиваются средние межатомные расстояния, в результате чего возникают силы притяжения между частицами, и тело стремится вернуться к первоначальным размерам. Деформация тела называется упругой, если после снятия нагрузки тело возвращается к первоначальным размерам и форме. Строго говоря, остаточная деформация есть всегда, но если она мала, ею пренебрегают. При неупругой деформации происходит разрыв некоторых межатомных связей и образование связей между другими атомами, в результате чего изменённая форма тела сохраняется и после снятия нагрузки. Любая деформация может быть представлена как сочетание двух основных: растяжения (сжатия) и сдвига (рис.2.5 и 2.6 соответственно). Рассмотрим деформацию растяжения стержня. При малых деформациях изменение длины тела, то есть абсолютная деформация 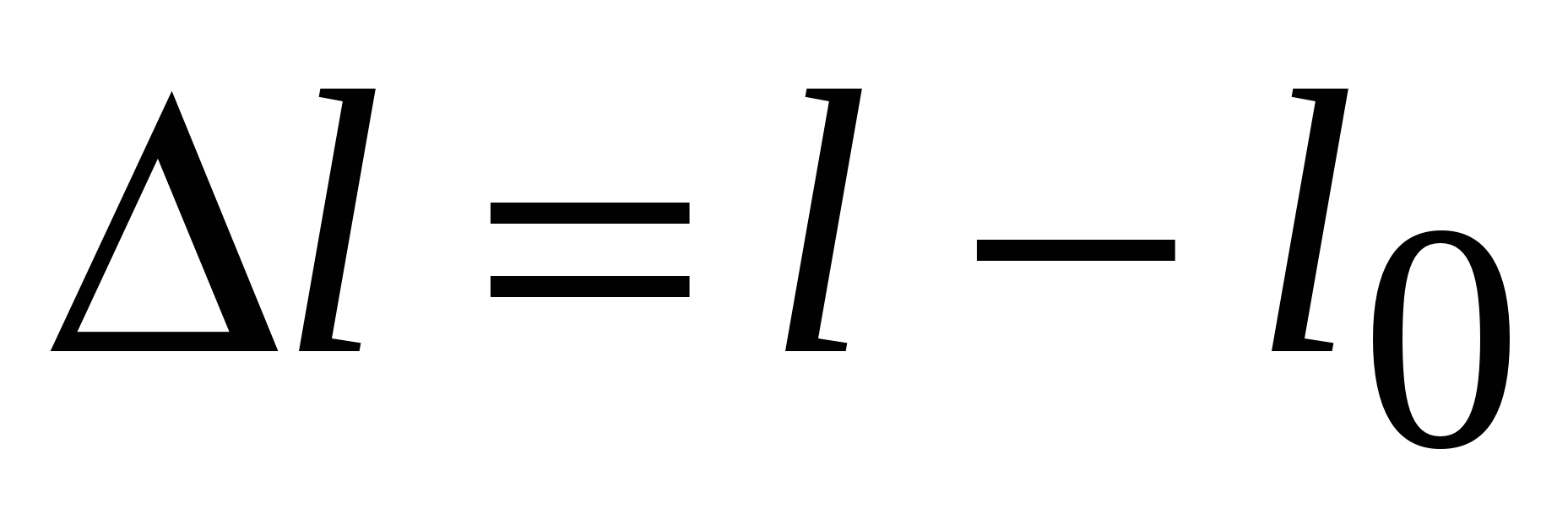 , прямо пропорциональна приложенной силе – это закон Гука:
, прямо пропорциональна приложенной силе – это закон Гука: 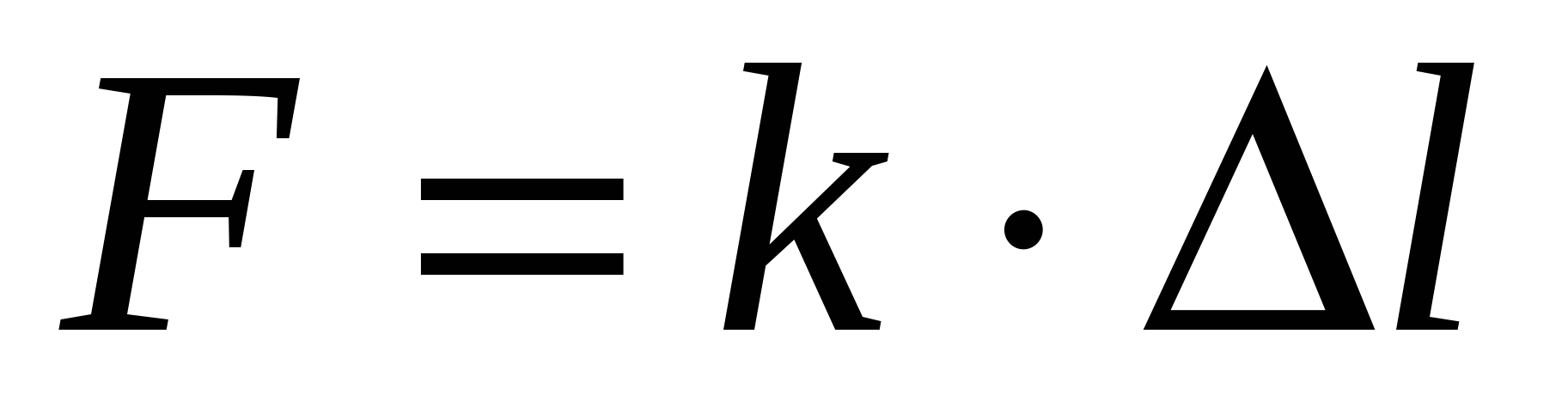 ; (2.14) здесь
; (2.14) здесь  – жёсткость. Закон Гука можно записать в локальной форме. Для этого введём новые величины: 1. Механическое нормальное напряжение σ – это сила, приходящаяся на единицу площади сечения тела (считаем силу приложенной перпендикулярно сечению
– жёсткость. Закон Гука можно записать в локальной форме. Для этого введём новые величины: 1. Механическое нормальное напряжение σ – это сила, приходящаяся на единицу площади сечения тела (считаем силу приложенной перпендикулярно сечению 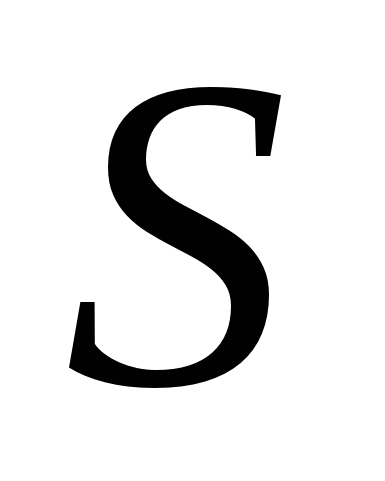 ):
): 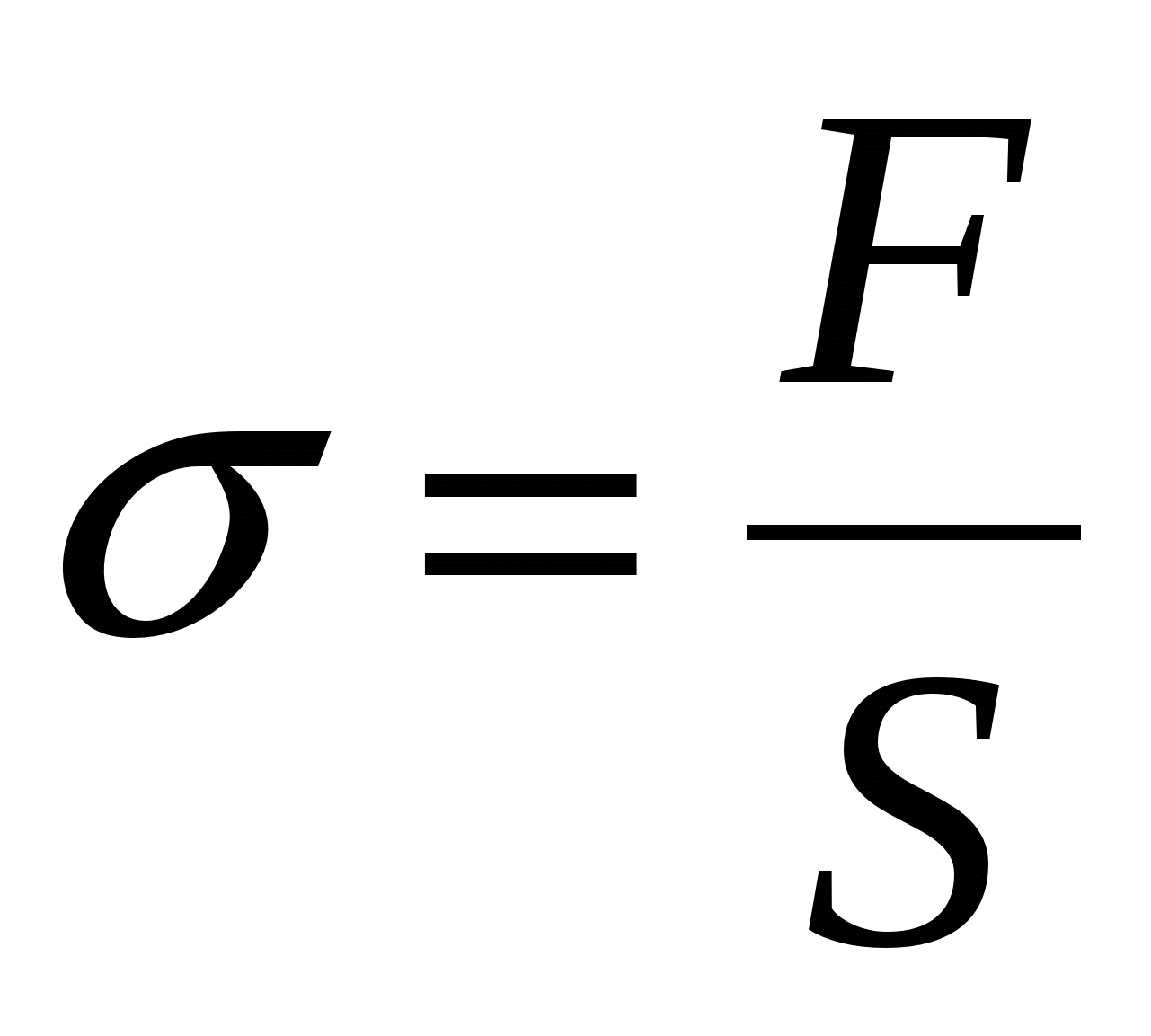 . (2.15) Механическое напряжение – локальная характеристика; в разных точках сечения оно, вообще говоря, может быть различным, поэтому лучше использовать определение (2.15а):
. (2.15) Механическое напряжение – локальная характеристика; в разных точках сечения оно, вообще говоря, может быть различным, поэтому лучше использовать определение (2.15а): 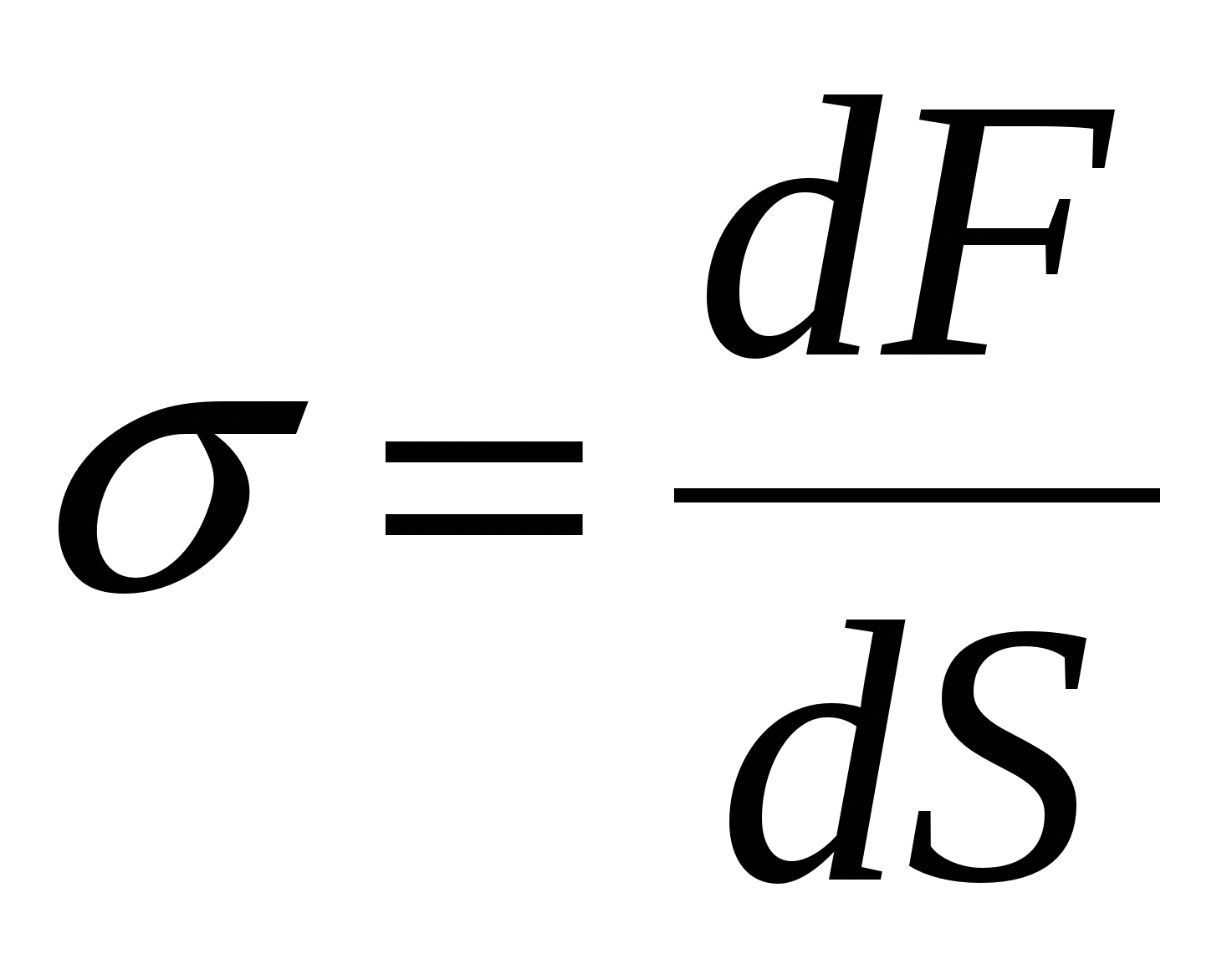 . (2.15а) Размерность
. (2.15а) Размерность 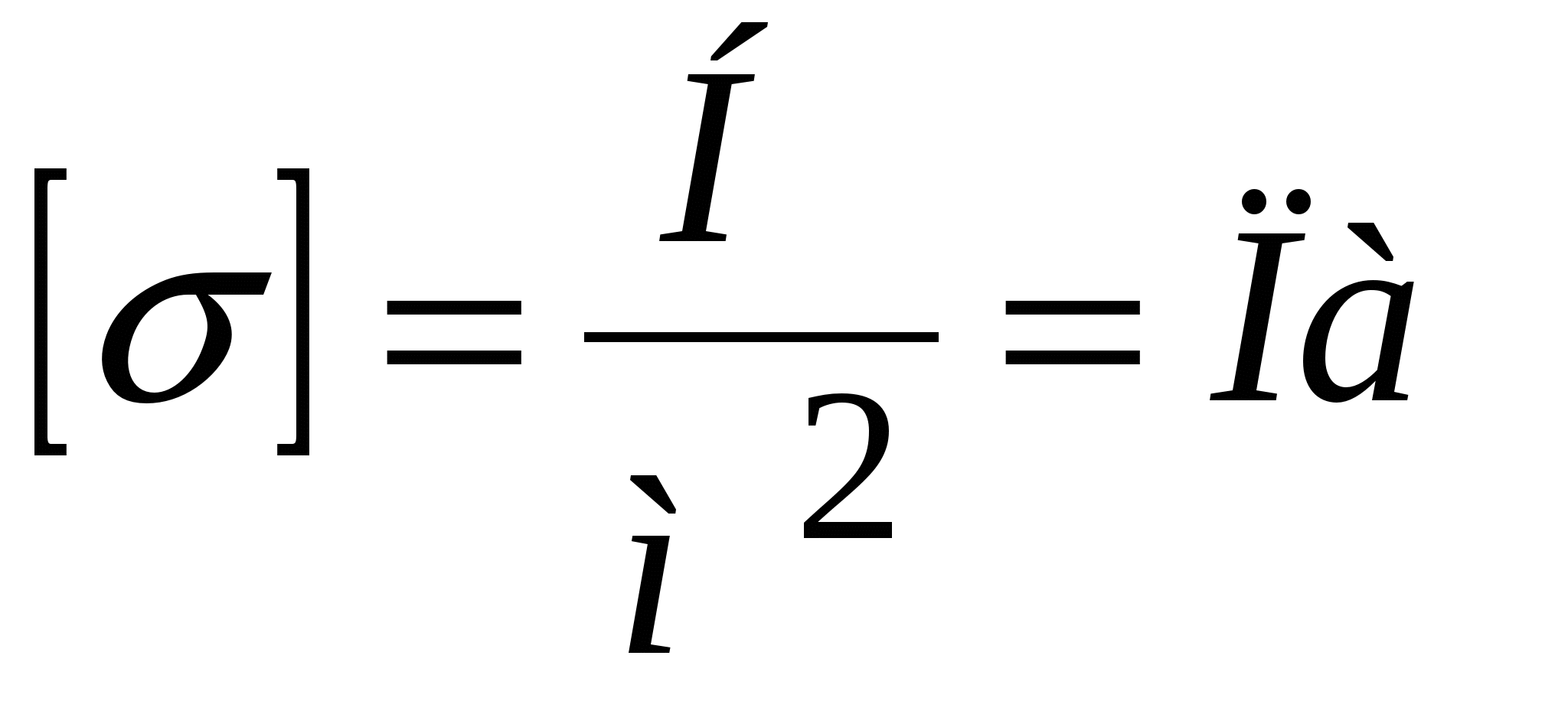 . 2. Относительная продольная деформация
. 2. Относительная продольная деформация  (или просто
(или просто 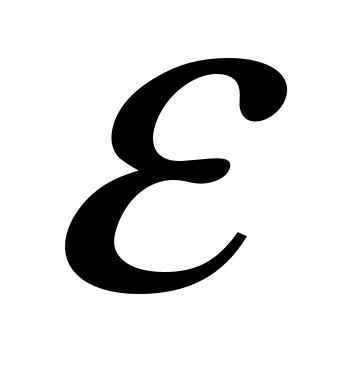 ) – это изменение длины по отношению к первоначальной длине:
) – это изменение длины по отношению к первоначальной длине: 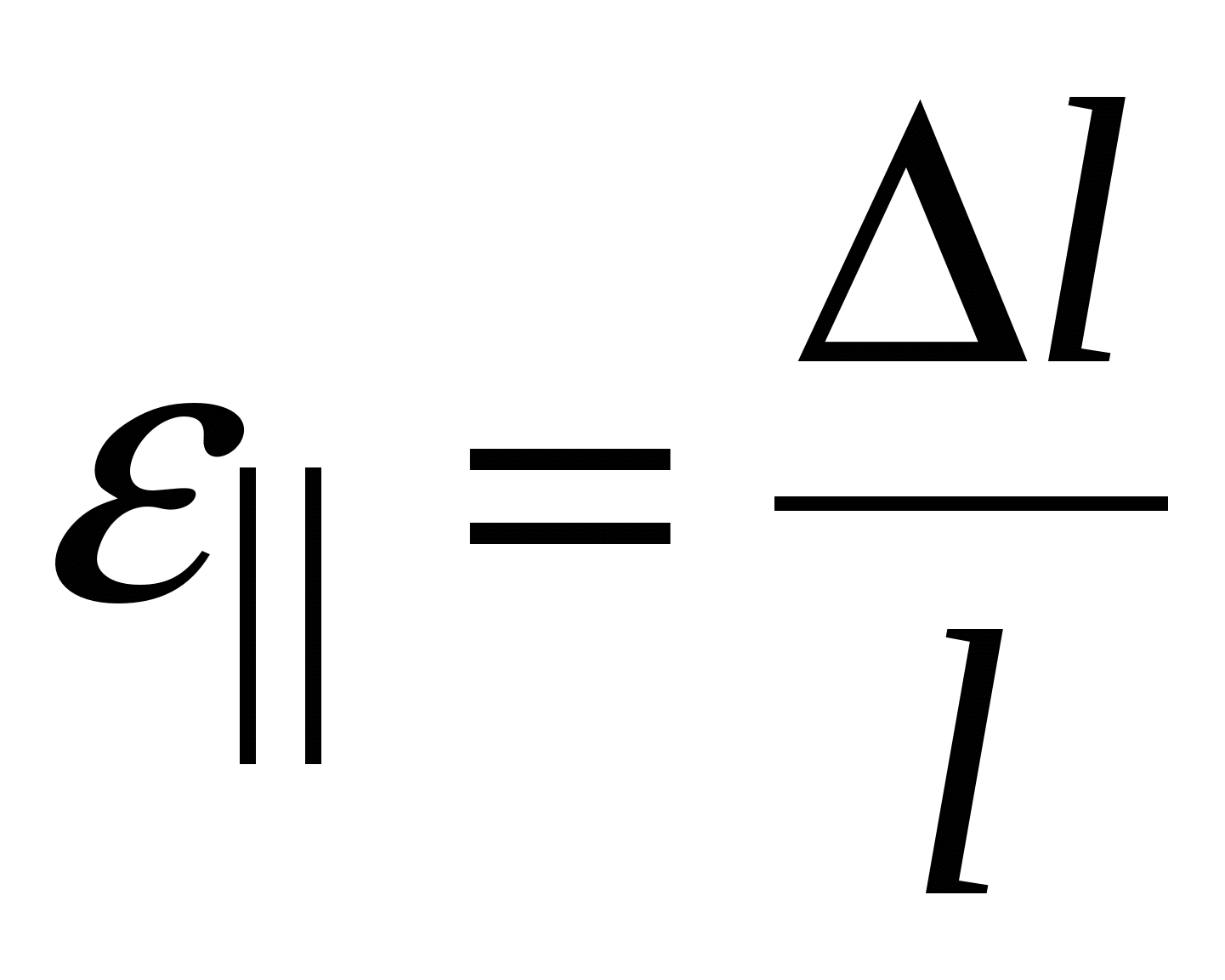 . (2.16) Она безразмерна:
. (2.16) Она безразмерна: 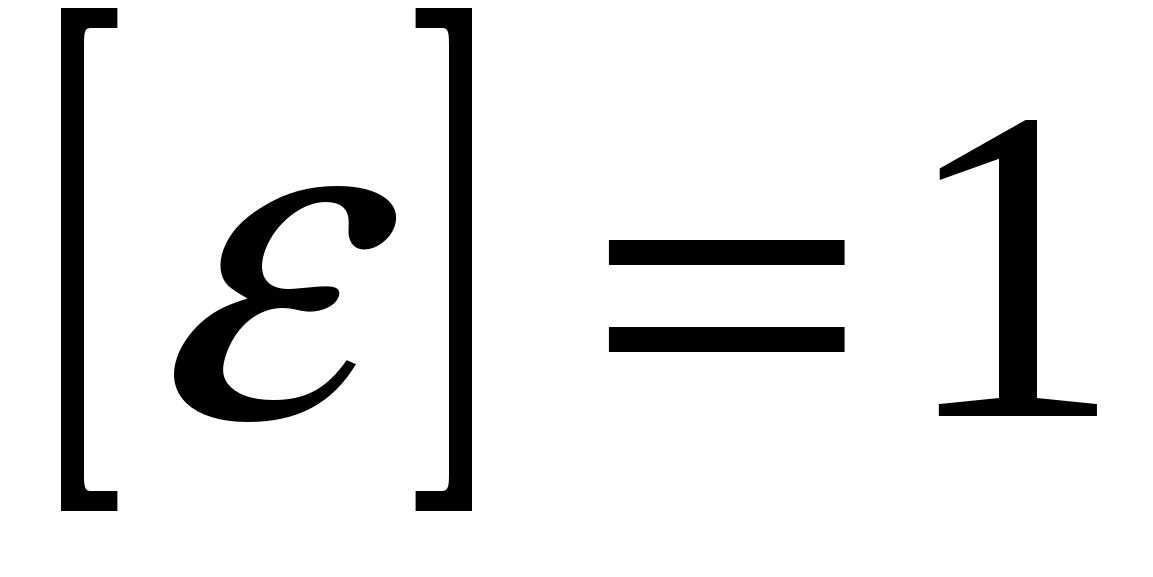 . Тогда закон Гука в локальной форме читается так: механическое напряжение прямо пропорционально относительной деформации:
. Тогда закон Гука в локальной форме читается так: механическое напряжение прямо пропорционально относительной деформации: 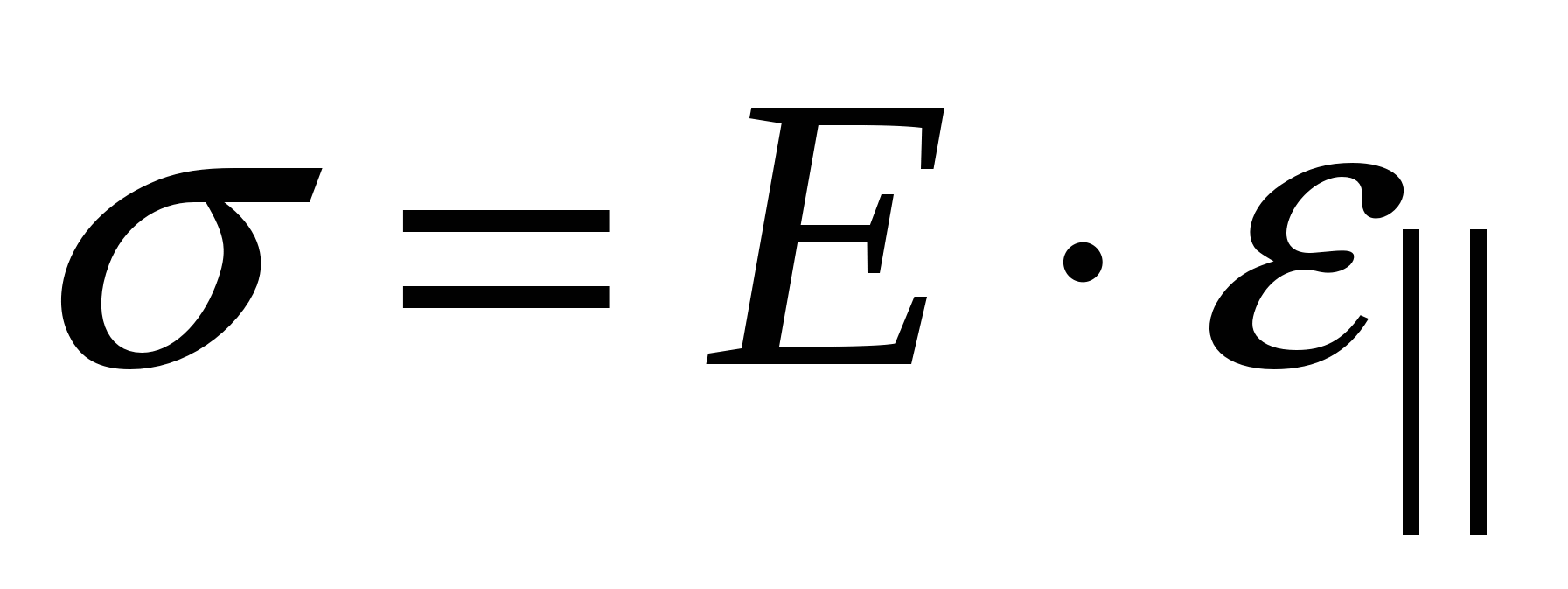 (2.17) Величина
(2.17) Величина  – это модуль Юнга материала и характеризует упругие свойства этого материала; не зависит от размеров и формы образца, в отличие от жёсткости
– это модуль Юнга материала и характеризует упругие свойства этого материала; не зависит от размеров и формы образца, в отличие от жёсткости  (2.18), и поэтому формулировка (2.17) более удобна и универсальна, чем (2.14). Можно найти соотношение между жёсткостью и модулем Юнга:
(2.18), и поэтому формулировка (2.17) более удобна и универсальна, чем (2.14). Можно найти соотношение между жёсткостью и модулем Юнга: 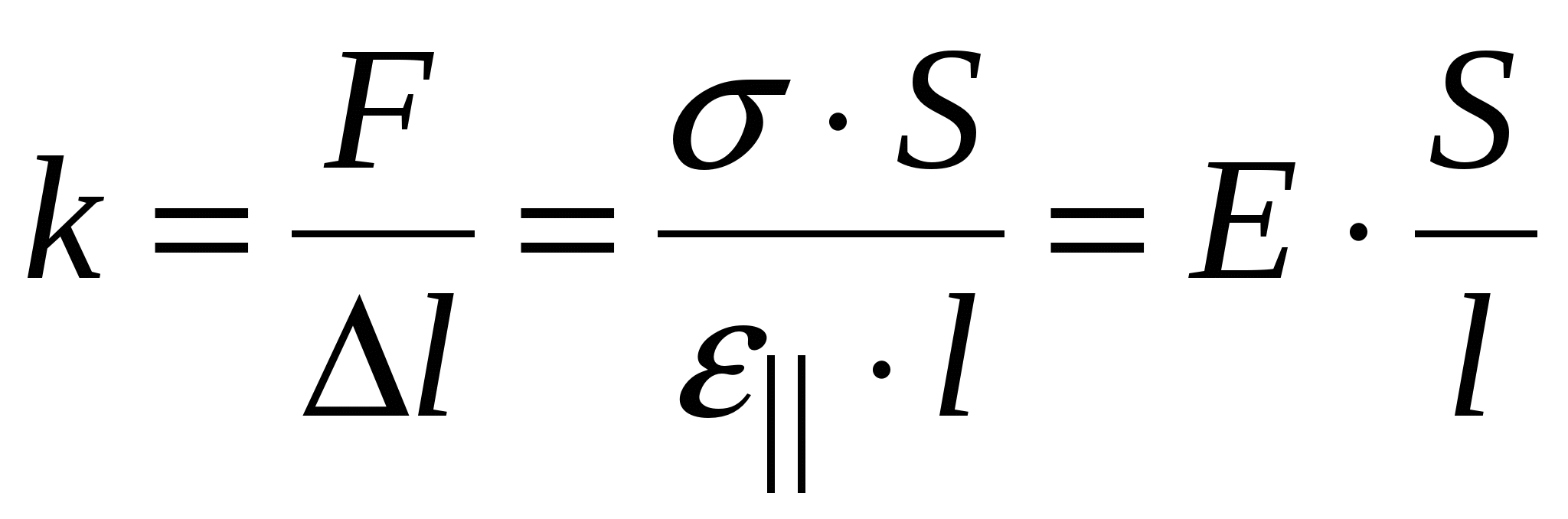 . (2.18) Размерность модуля Юнга:
. (2.18) Размерность модуля Юнга: 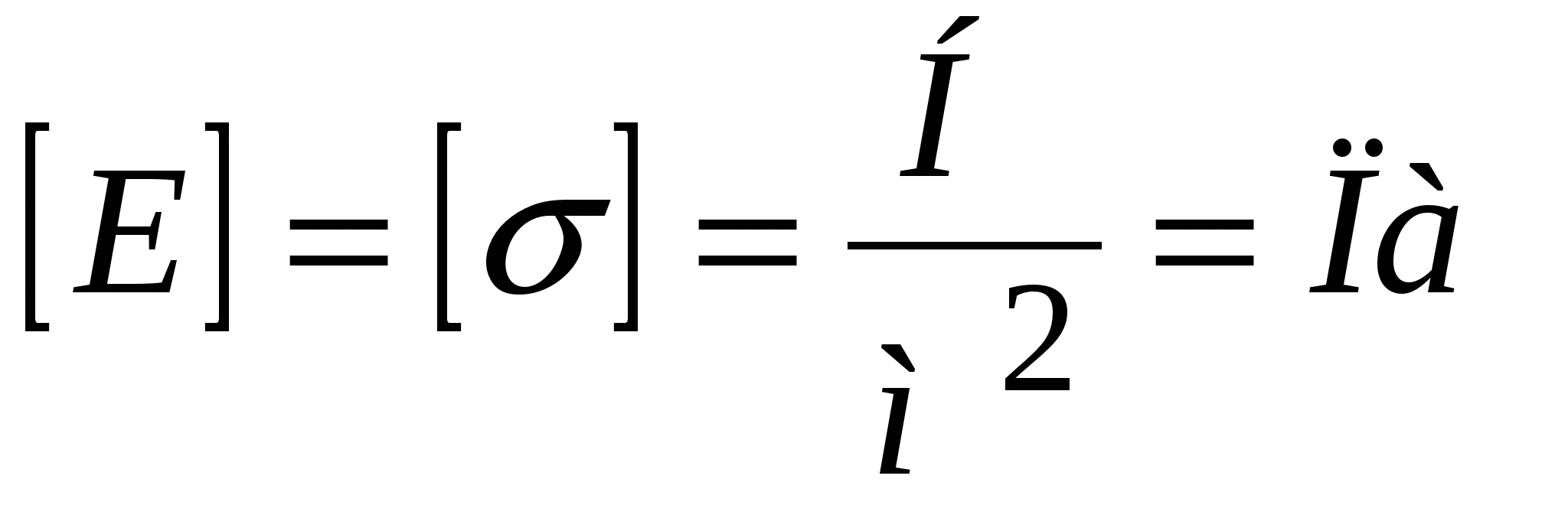 . Экспериментальная зависимость механического напряжения от относительной продольной деформации дана на рис.2.7. Там же указаны характерные точки – пределы: пропорциональности
. Экспериментальная зависимость механического напряжения от относительной продольной деформации дана на рис.2.7. Там же указаны характерные точки – пределы: пропорциональности 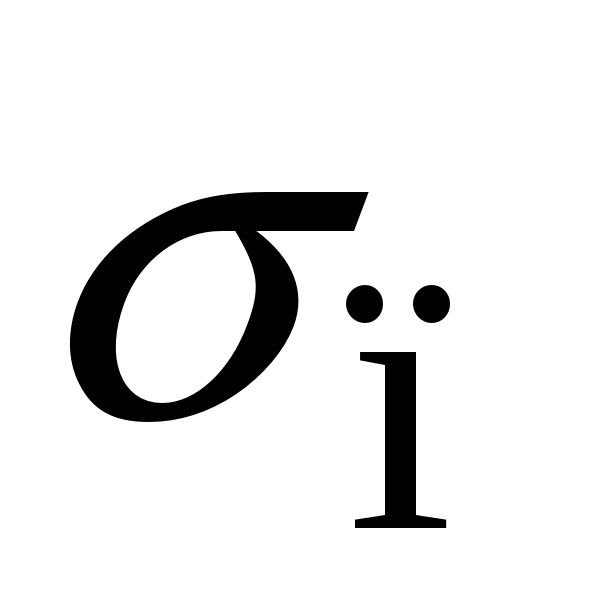 , упругости
, упругости 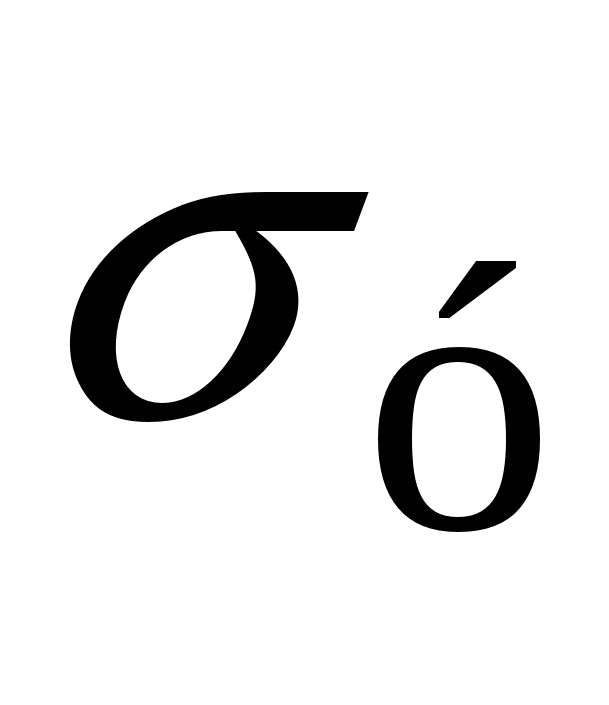 , текучести
, текучести 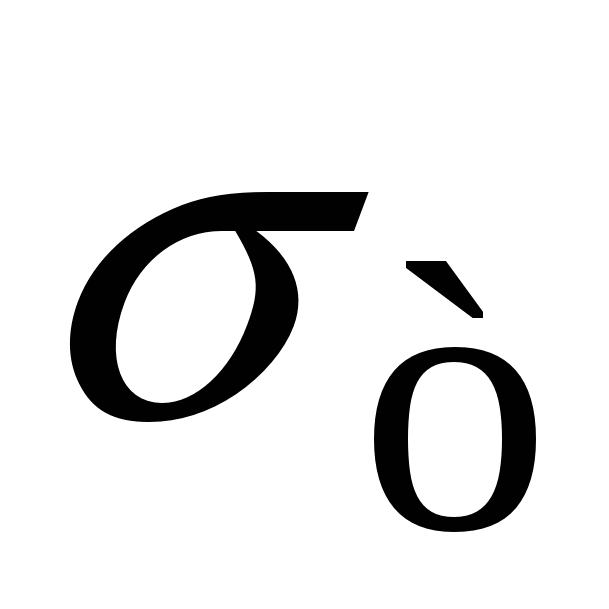 и прочности
и прочности 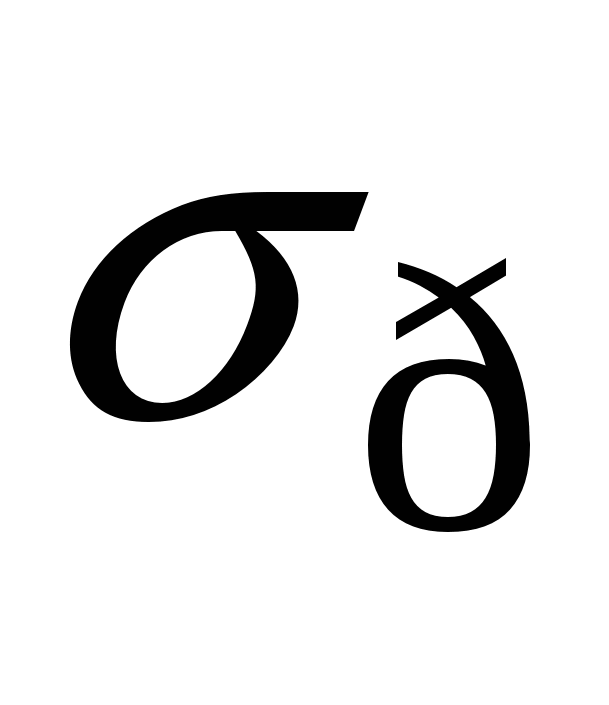 . Предел пропорциональности
. Предел пропорциональности 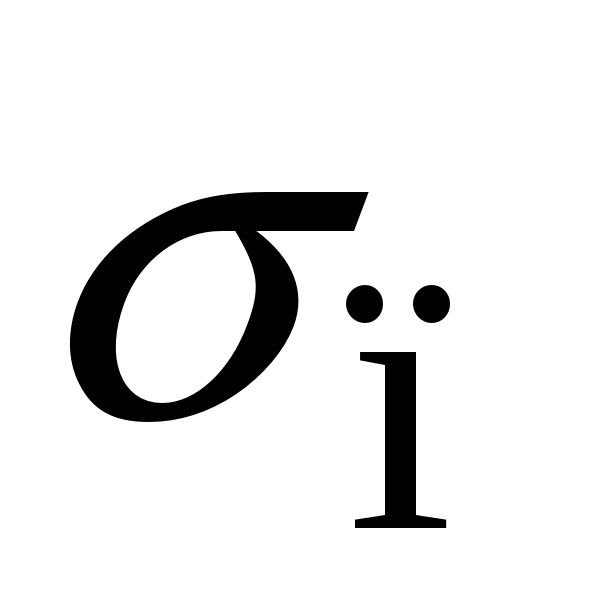 – это максимальное механическое напряжение, при котором ещё выполняется закон Гука (деформацию можно считать пропорциональной напряжению). Предел упругости
– это максимальное механическое напряжение, при котором ещё выполняется закон Гука (деформацию можно считать пропорциональной напряжению). Предел упругости 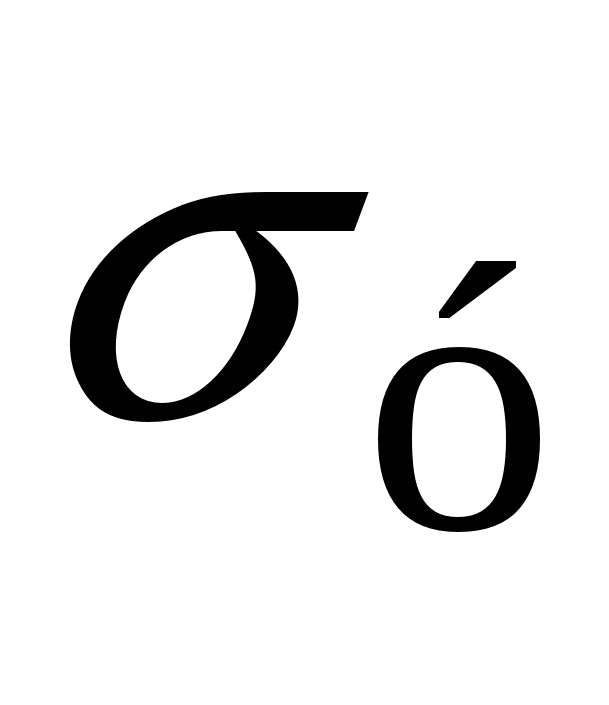 – такое максимальное напряжение, при котором деформацию можно считать упругой. Если напряжение превысит этот предел, после снятия нагрузки будет остаточная деформация. Предел текучести
– такое максимальное напряжение, при котором деформацию можно считать упругой. Если напряжение превысит этот предел, после снятия нагрузки будет остаточная деформация. Предел текучести 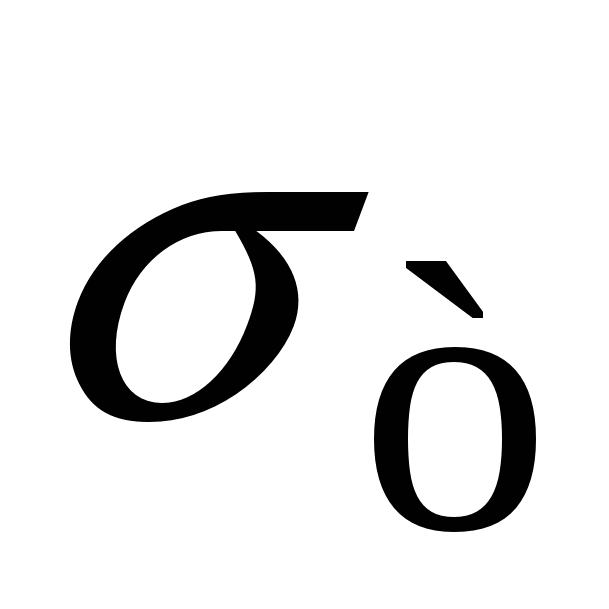 – это механическое напряжение, при котором деформация увеличивается почти без увеличения нагрузки. Горизонталь на графике – это область пластичности. Если тело пластично, этот участок длинный (сталь), если горизонтальный участок мал – тело хрупкое (чугун). Предел прочности
– это механическое напряжение, при котором деформация увеличивается почти без увеличения нагрузки. Горизонталь на графике – это область пластичности. Если тело пластично, этот участок длинный (сталь), если горизонтальный участок мал – тело хрупкое (чугун). Предел прочности 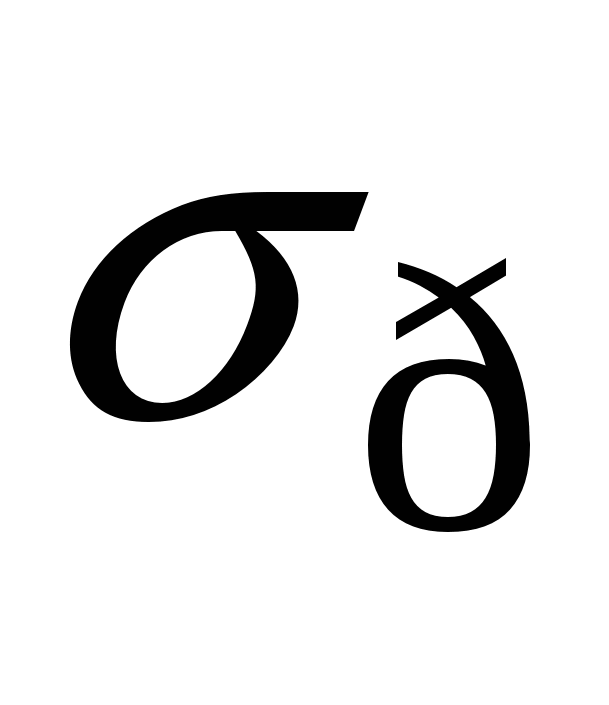 – это напряжение, при котором начинается разрушение тела. При деформации (удлинении) тела изменяется (уменьшается) сечение, и вообще говоря, изменяется объём. Относительное поперечное сжатие – это
– это напряжение, при котором начинается разрушение тела. При деформации (удлинении) тела изменяется (уменьшается) сечение, и вообще говоря, изменяется объём. Относительное поперечное сжатие – это 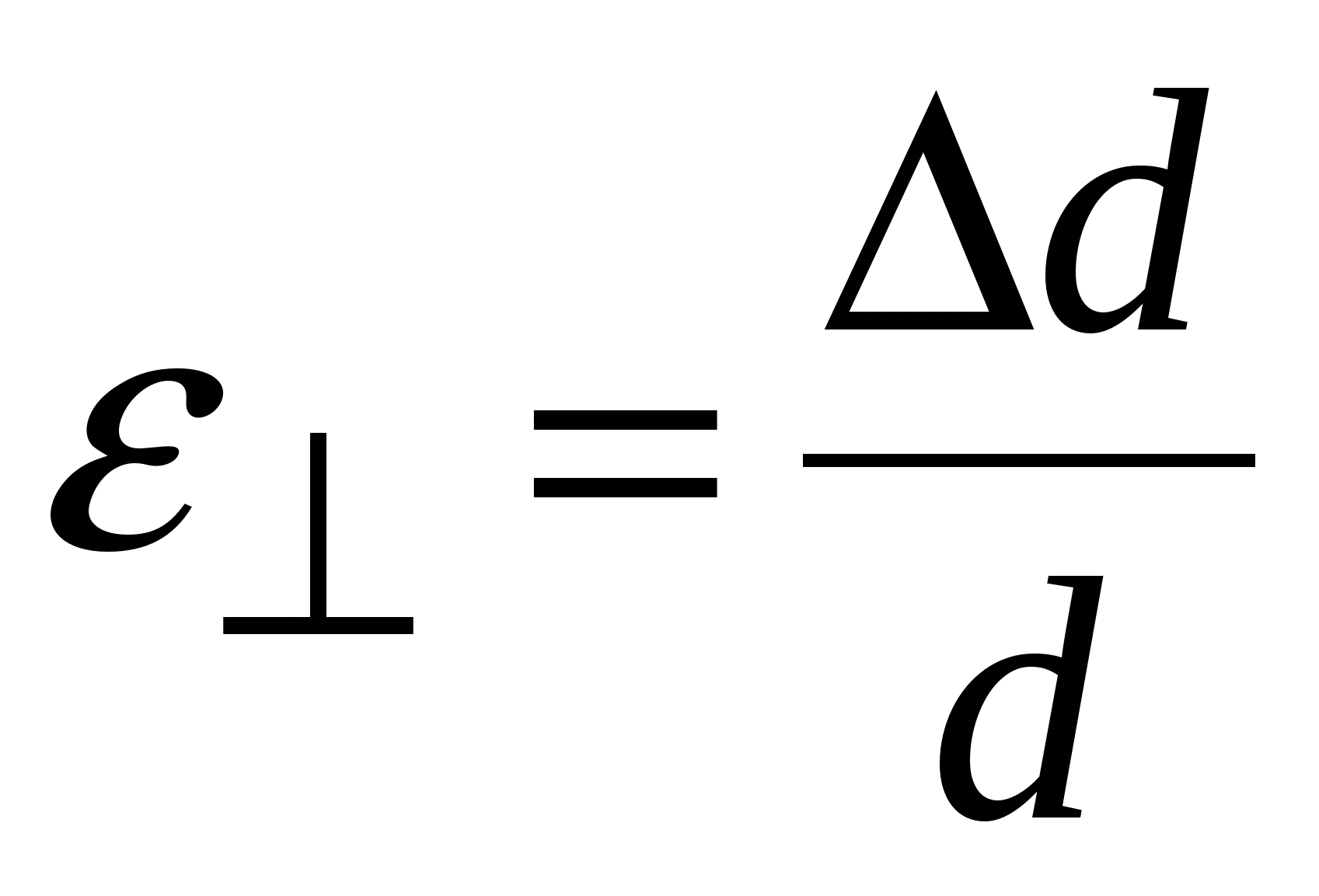 . (2.19) При односторонней деформации величины
. (2.19) При односторонней деформации величины 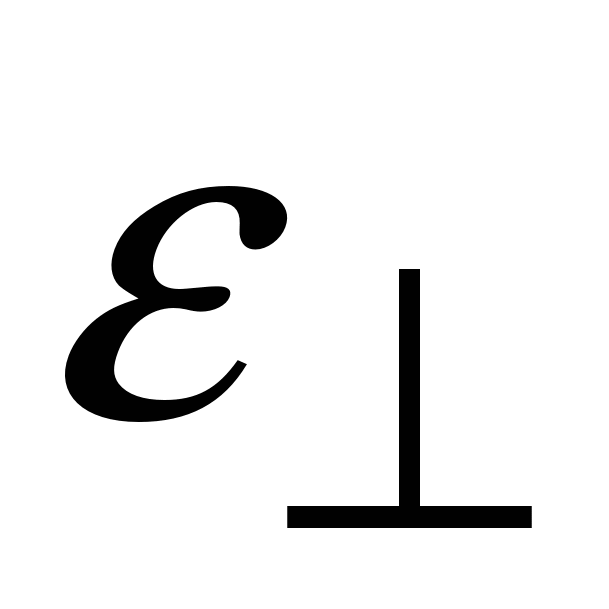 и
и  имеют противоположные знаки: при растяжении сечение уменьшается. Отношение этих величин – коэффициент Пуассона материала:
имеют противоположные знаки: при растяжении сечение уменьшается. Отношение этих величин – коэффициент Пуассона материала: 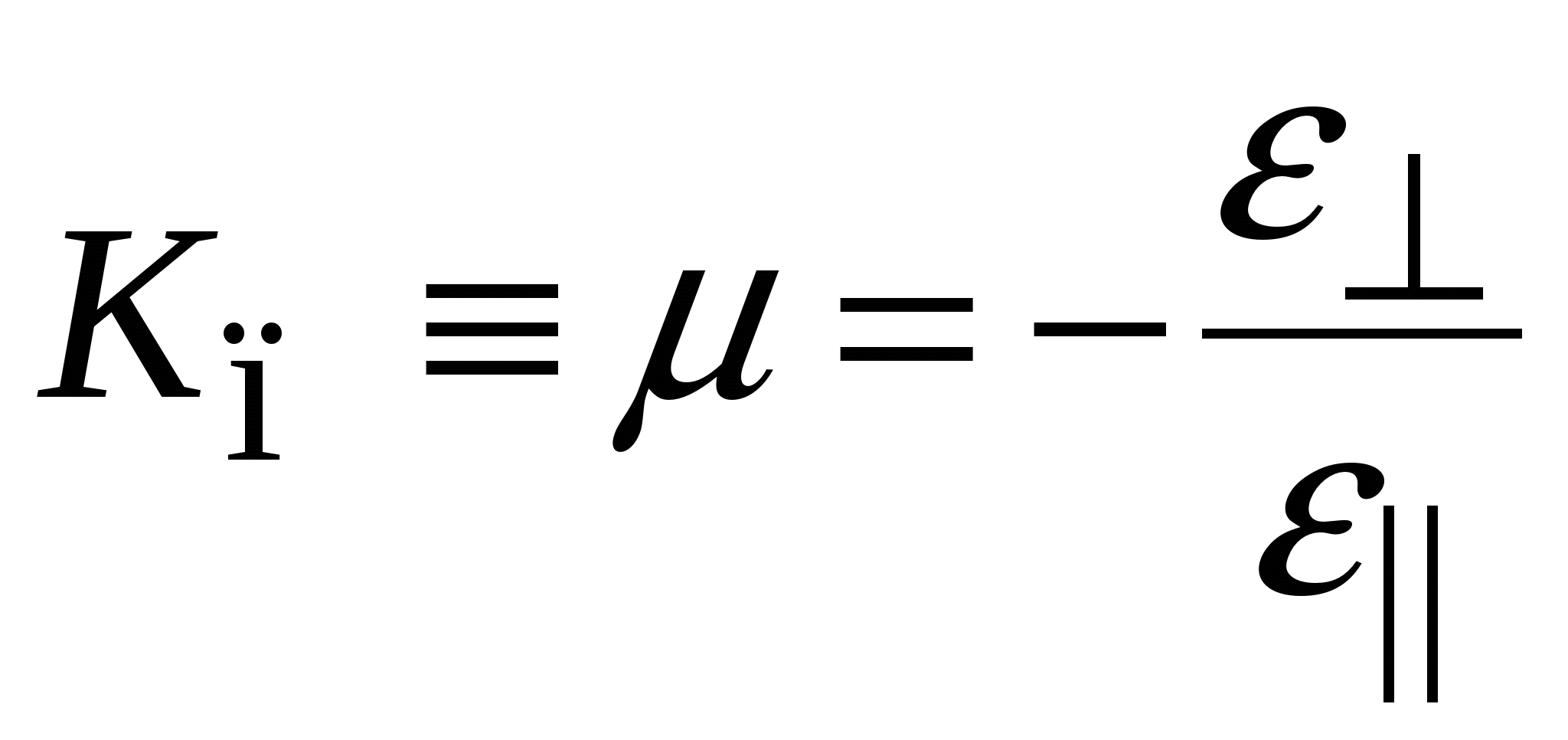 . (2.20) Можно доказать, что коэффициент Пуассона материалов, сохраняющих объём при деформациях, равен
. (2.20) Можно доказать, что коэффициент Пуассона материалов, сохраняющих объём при деформациях, равен 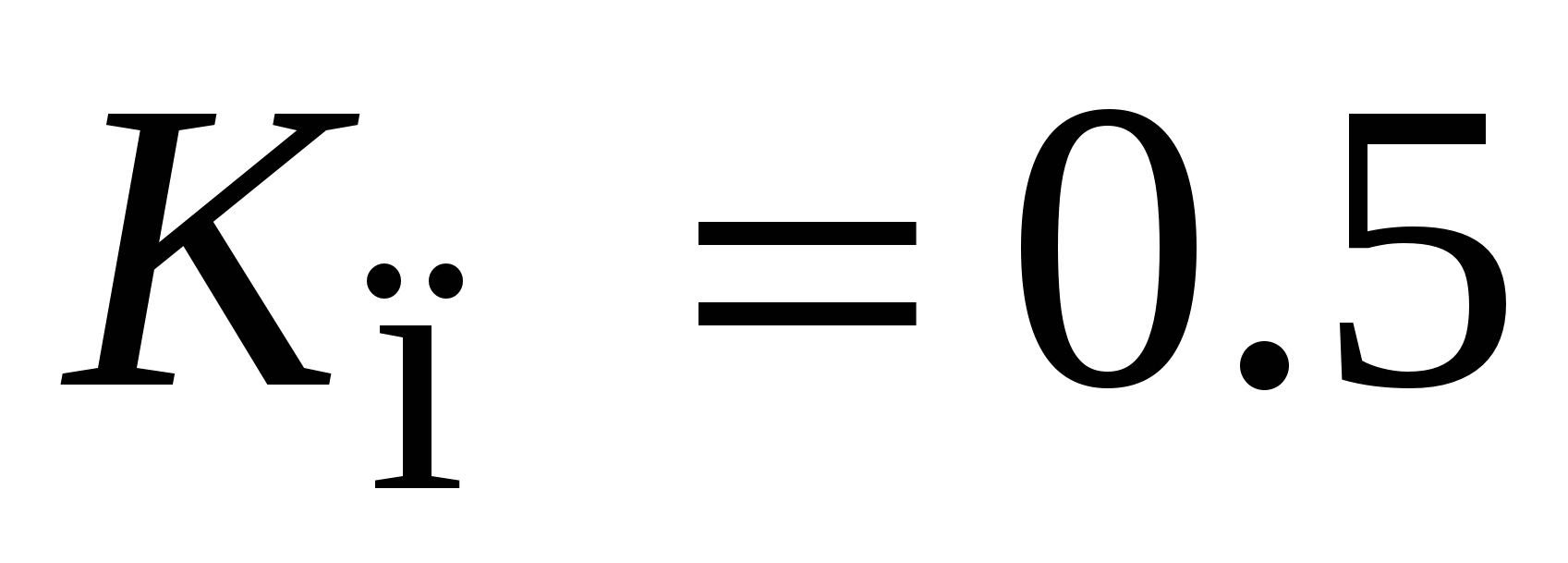 .
. 
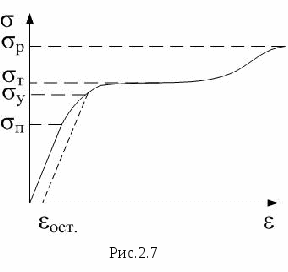
4. Момент инерции материальной точки относительно оси вращения - произведение массы этой точки на квадрат расстояния от оси.
При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела, так и от положения и направления оси вращения.
Момент инерции твердого тела - это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.
Формула момента инерции:
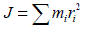
Единица момента инерции - килограмм-метр в квадрате.
Теорема Штейнера:
Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R - расстояние между осями.
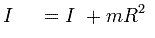
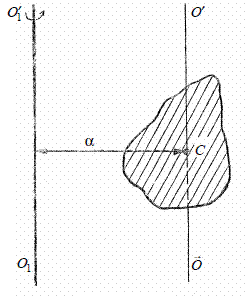
Угловое ускорение, которое тело приобретает под действием момента сил, прямо пропорционально результирующему моменту всех внешних сил, приложенных к телу, и обратно пропорциональна моменту инерции тела относительно некоторой оси.
Молекулярная физика
Вещество может находиться в трех агрегатных состояниях: твердом, жидком и газообразном. Молекулярная физика - раздел физики, в котором изучаются физические свойства тел в различных агрегатных состояниях на основе их молекулярного строения.
Тепловое движение - беспорядочное (хаотическое) движение атомов или молекул вещества.
МАССА И РАЗМЕРЫ МОЛЕКУЛ
Массы молекул и атомов очень малы. Например, масса одной молекулы водорода равна примерно 3,34*10 -27 кг, кислорода - 5,32*10 -26 кг. Масса одного атома углерода m0C=1,995*10 -26 кг
Относительной молекулярной (или атомной) массой вещества Mr называют отношение массы молекулы (или атома) данного вещества к 1/12 массы атома углерода:(атомная единица массы).
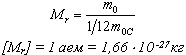
Количество вещества - это отношение числа молекул N в данном теле к числу атомов в 0,012 кг углерода NA:
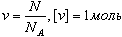
Моль - количество вещества, содержащего столько молекул, сколько содержится атомов в 0,012 кг углерода.
Число молекул или атомов в 1 моле вещества называют постоянной Авогадро:
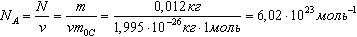
Молярная масса - масса 1 моля вещества:
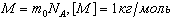
Молярная и относительная молекулярная массы вещества связаны соотношением: М = Мr*10 -3 кг/моль.
СКОРОСТЬ ДВИЖЕНИЯ МОЛЕКУЛ
Несмотря на беспорядочный характер движения молекул, их распределение по скоростям носит характер определенной закономерности, которая называется распределением Максвелла.
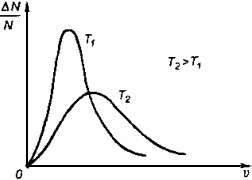
График, характеризующий это распределение, называют кривой распределения Максвелла. Она показывает, что в системе молекул при данной температуре есть очень быстрые и очень медленные, но большая часть молекул движется с определенной скоростью, которая называется наиболее вероятной. При повышении температуры эта наиболее вероятная скорость увеличивается.
ТЕМПЕРАТУРА
Любое макроскопическое тело или группа макроскопических тел называется термодинамической системой.
Тепловое или термодинамическое равновесие - такое состояние термодинамической системы, при котором все ее макроскопические параметры остаются неизменными: не меняются объем, давление, не происходит теплообмен, отсутствуют переходы из одного агрегатного состояния в другое и т.д. При неизменных внешних условиях любая термодинамическая система самопроизвольно переходит в состояние теплового равновесия.
Температура - физическая величина, характеризующая состояние теплового равновесия системы тел: все тела системы, находящиеся друг с другом в тепловом равновесии, имеют одну и ту же температуру.
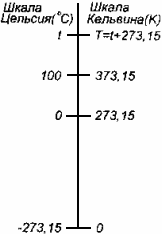
Абсолютный нуль температуры - предельная температура, при которой давление идеального газа при постоянном объеме должно быть равно нулю или должен быть равен нулю объем идеального газа при постоянном давлении.
Термометр - прибор для измерения температуры. Обычно термометры градуируют по шкале Цельсия: температуре кристаллизации воды (таяния льда) соответствует 0°С, температуре ее кипения - 100°С.
Кельвин ввел абсолютную шкалу температур, согласно которой нулевая температура соответствует абсолютному нулю, единица измерения температуры по шкале Кельвина равна градусу Цельсия: [Т] = 1 К (Кельвин).
Связь температуры в энергетических единицах и температуры в градусах Кельвина:
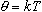
где k = 1,38*10 -23 Дж/К - постоянная Больцмана.
Связь абсолютной шкалы и шкалы Цельсия:
T = t + 273
где t - температура в градусах Цельсия.
Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре:
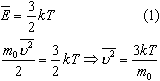
Средняя квадратичная скорость молекул
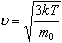
Учитывая равенство (1), основное уравнение молекулярно-кинетической теории можно записать так:
p=nkT
Закон Ома
Однородный участок цепи — это участок цепи, который не имеет источника тока. Напряжение на таком участке будет определяться разностью потенциалов на его концах, т. е.: 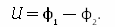
В 1826 г. немецкий ученый Г. Ом открыл закон, который определяет соотношение между силой тока в однородном участке цепи и напряжением на нем: сила тока в проводнике прямо пропорциональна напряжению на нем. 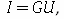 , где G — коэффициент пропорциональности, который называется в этом законе электропроводностью или проводимостью проводника, которая определяется формулой.
, где G — коэффициент пропорциональности, который называется в этом законе электропроводностью или проводимостью проводника, которая определяется формулой.
Электропроводность проводника — это физическая величина, которая является обратной его сопротивлению.
В Международной системе единиц единицей измерения электропроводности является сименс (См).
Физический смысл сименса: 1 См — это проводимость проводника сопротивлением 1 Ом.
Чтобы получить закон Ома для участка цепи, необходимо подставить в формулу, приведенную выше, вместо электропроводности сопротивление R, тогда: 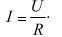
Закон Ома для участка цепи: сила тока в участке цепи прямо пропорциональна напряжению на нем и обратно пропорциональна сопротивлению участка цепи.
Закон Ома для полной цепи: сила тока в неразветвленной замкнутой цепи, включающая источник тока, прямо пропорциональна электродвижущей силе этого источника и обратнопропорциональна сумме внешнего и внутреннего сопротивлений данной цепи: 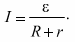
Правила знаков:
Если при обходе цепи в выбранном направлении ток внутри источника идет в направлении обхода, то ЭДС этого источника считается положительной.
Если при обходе цепи в выбранном направлении ток внутри источника идет в противоположном направлении, то ЭДС этого источника считается отрицательной.
Электродвижущая сила (ЭДС) — это физическая величина, которая характеризует действие сторонних сил в источниках тока, это энергетическая характеристика источника тока. Для замкнутого контура ЭДС определяется как отношение работы сторонних сил по перемещению положительного заряда вдоль замкнутого контура к этому заряду: 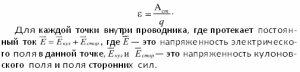
В Международной системе единиц единицей измерения ЭДС является вольт. При разомкнутой цепи ЭДС источника тока равна электрическому напряжению на его зажимах.
Закон Джоуля—Ленца: количество теплоты, выделяемое проводником с током, определяется произведением квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику: 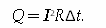
При перемещении электрическое поле заряда по участку цепи делает работу, которая определяется произведением заряда на напряжение на концах этого участка цепи: 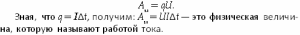
Мощность постоянного тока — это физическая величина, которая характеризует скорость совершения полем работы по перемещению заряженных частиц по проводнику и определяется отношением работы тока за время к этому промежутку времени: 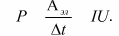
Правила Кирхгофа, которые применяются для расчета разветвленных цепей постоянного тока, суть которого заключается в отыскании по заданным сопротивлениям участков цепи и приложенным к ним ЭДС сил токов в каждом участке.
Первое правило — правило узлов: алгебраическая сумма токов, которые сходятся в узле, — это точка, в которой есть более двух возможных направлений тока,она равна нулю 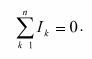
Второе правило — правило контуров: в любом замкнутом контуре, в разветвленной электрической цепи алгебраическая сумма произведений сил токов на сопротивление соответствующих участков этого контура определяется алгебраической суммой приложенных в нем ЭДС: 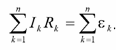
Магнитное поле — это одна из форм проявления электромагнитного поля, специфика которой состоит в том, что это поле воздействует только на движущиеся частицы и тела, имеющие электрический заряд, а также на намагниченные тела независимо от состояния их движения.
Вектор магнитной индукции — это векторная величина, которая характеризует магнитное поле в любой точке пространства, определяющая отношение силы, действующей со стороны магнитного поля на элемент проводника с электрическим током, к произведению силы тока и длины элемента проводника, равная по модулю отношению магнитного потока сквозь поперечное сечение площади к площади этого поперечного сечения.
В Международной системе единиц единицей индукции является тесла (Тл).
Магнитная цепь — это совокупность тел или областей пространства, где сосредоточено магнитное поле.
Магнитный поток (поток магнитной индукции) — это физическая величина, которая определяется произведением модуля вектора магнитной индукции на площадь плоской поверхности и на косинус угла между векторами нормали к плоской поверхности / угол между вектором нормали и направлением вектора индукции.
В Международной системе единиц единицей магнитного потока является вебер (Вб).
Теорема Остроградского—Гаусса для потока магнитной индукции: магнитный поток сквозь произвольную замкнутую поверхность равен нулю: 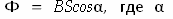
Закон Ома для замкнутой магнитной цепи: 
Магнитная проницаемость — это физическая величина, которая характеризует магнитные особенности вещества, которая определяется отношением модуля вектора магнитной индукции в среде к модулю вектора индукции в той же точке пространства в вакууме: 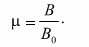
Напряженность магнитного поля — это векторная величина, которая определяет и характеризует магнитное поле и равна: 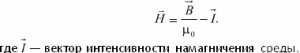
Сила Ампера — это сила, которая действует со стороны магнитного поля на проводник с током. Элементарная сила Ампера определяется соотношением: 
Закон Ампера: модуль силы, воздействующей на небольшой отрезок проводника, по которому течет ток, со стороны однородного магнитного поля с индукцией, составляющей с элементом угол 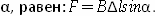
Принцип суперпозиции: когда в данной точке пространства многообразные источники формируют магнитные поля, индукции которых В1,В2, .., то результирующая индукция поля в этой точке равна: 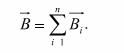
Правило буравчика или правило правого винта: если направление поступательного движения острия буравчика при ввинчивании совпадает с направлением тока в пространстве, то направление вращательного движения буравчика в каждой точке совпадает с направлением вектора магнитной индукции.
Закон Био—Савара—Лапласа: определяет величину и направление вектора магнитной индукции в любой точке магнитного поля, создаваемого в вакууме элементом проводника определенной длины с током: 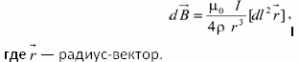
Движение заряженных частиц в электрическом и магнитном полях Сила Лоренца — это сила, влияющая на движущуюся частицу со стороны магнитного поля: 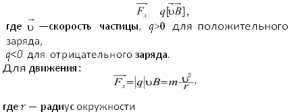
Правило левой руки:
Необходимо располагать левую руку так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца были сонаправлены с током, тогда отогнутый на 90° большой палец укажет направление силы Ампера.
Необходимо располагать левую руку так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца совпадали с направлением скорости частицы при положительном заряде частицы или были направлены в сторону, противоположную скорости частицы при отрицательном заряде частицы, тогда отогнутый на 90° большой палец покажет направление силы Лоренца, действующей на заряженную частицу.
Если происходит совместное действие на движущийся заряд электрического и магнитного полей, то результирующая сила будет определяться: 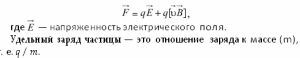
Масс-спектрографы и масс-спектрометры — это приборы, которые предназначены специально для точных измерений относительных атомных масс элементов.
Самоиндукция. Индуктивность
Самоиндукция — это явление, состоящее в том, что изменяющееся магнитное поле индуцирует ЭДС в том самом проводнике, по которому течет ток, образовывающий это поле.
Магнитный поток Ф контура с током I определяется:
Ф = L, где L — это коэффициент самоиндукции (индуктивность тока).
Индуктивность — это физическая величина, которая является характеристикой ЭДС самоиндукции, появляющейся в контуре при изменении силы тока, определяется отношением магнитного потока через поверхность, ограниченную проводником, к силе постоянного тока в цепи: 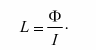
В Международной системе единиц единицей измерения индуктивности является генри (Гн).
ЭДС самоиндукции определяется: 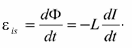
Энергия магнитного поля определяется: 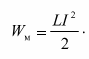
Объемная плотность энергии 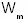 магнитного поля в изотропной и неферромагнитной среде определяется:
магнитного поля в изотропной и неферромагнитной среде определяется: 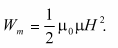
Законы постоянного тока
ЭЛЕКТРИЧЕСКИЙ ТОК
Электрический ток - это упорядоченное движение заряженных частиц.
За направление тока принято направление движения положительных зарядов.
Электрический ток вызывает нагревание проводника. Вокруг проводника с током существует магнитное поле. Электрический ток способен оказывать химическое действие.
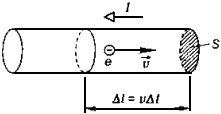
Сила тока - заряд, переносимый через поперечное сечение проводника в единицу времени:
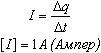
При токе 1 А через поперечное сечение проводника за 1 с проходит заряд 1 Кл.
За время Δt через поперечное сечение проводника S проходят заряженные частицы, содержащиеся в объеме

где  - их средняя скорость направленного движения.
- их средняя скорость направленного движения.
Если заряд каждой частицы равен q 0, а их концентрация n, то общий заряд, прошедший через поперечное сечение проводника за время t равен
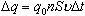
Отсюда сила тока
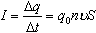
Электрический ток возникает при наличии свободных заряженных частиц и электрического поля.
Концентрация свободных носителей заряда в проводниках существенно выше, чем в диэлектриках. Для создания стационарного электрического поля внутри проводника между его концами должна поддерживаться разность потенциалов. Если она длительное время остается неизменной, то по проводнику проходит постоянный электрический ток.
Закон Ома для участка цепи
Сила тока прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению проводника R :
I=U/R
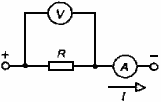
Сопротивление проводника равно 1 Ом, если при напряжении 1 В через него течет ток 1 А. Сопротивление R проводника прямо пропорционально его длине l и обратно пропорционально площади поперечного сечения S:
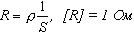
где ρ- удельное сопротивление материала
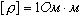
ЭЛЕКТРОДВИЖУЩАЯ СИЛА
Если два заряженных тела соединить проводником, то через него пойдет кратковременный ток. Избыточные электроны с отрицательно заряженного тела перейдут на положительно заряженное. Потенциалы тел окажутся одинаковыми, значит, напряжение на концах проводника станет равно нулю, и ток прекратится. Для существования длительного тока в проводнике нужно поддерживать разность потенциалов на его концах неизменной. Этого можно достичь, перенося свободные электроны с положительного тела на отрицательное так, чтобы заряды тел не менялись со временем.
Силы электрического взаимодействия сами по себе не способны осуществлять подобное разделение зарядов. Они вызывают притяжение электронов к положительному телу и отталкивание от отрицательного. Поэтому внутри источника тока должны действовать сторонние силы, имеющие неэлектрическую природу и обеспечивающие разделение электрических зарядов.
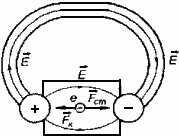
ЭДС источника равна сумме напряжений на внешнем и внутреннем участках цепи
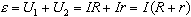
где r - внутреннее сопротивление источника.
Закон Ома для полной цепи
Сила тока прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи:
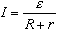
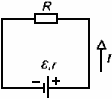
Работа сторонних сил по перемещению вдоль замкнутого контура заряда q = I ∆t равна
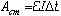
Она идет на нагревание внешнего и внутреннего участков цепи:
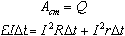
Сокращая , получаем: ε = IR + Ir .
В случае, когда последовательная цепь содержит несколько источников тока, результирующая ЭДС равна алгебраической сумме ЭДС источников с учетом их знаков: ε = ε1 + ε2 + ε3 + …, а внутреннее сопротивление - сумме всех их внутренних сопротивлений: r = r1 + r2 + r3 + … .
Пример. ЭДС батареи 6,0 В, ее внутреннее сопротивление 0,5 Ом, сопротивление внешней цепи 11,5 Ом. Найдите силу тока в цепи, напряжение на зажимах батареи и падение напряжения внутри батареи.
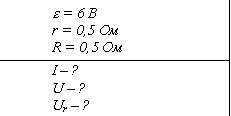
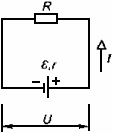
Пусть R - сопротивление внешнего участка цепи, r - внутреннее сопротивление батареи.
Тогда по закону Ома для замкнутой цепи
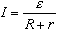
где ε - ЭДС батареи, I - сила тока в цепи. Так как сила тока I одинакова как для внешнего, так и для внутреннего участков цепи, то напряжение на зажимах батареи, т.е. на внешнем участке цепи с сопротивлением R , по закону Ома для этого однородного участка есть:
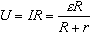
Аналогично, для внутреннего участка цепи, имеющего сопротивление r, можно записать U r= I*r. Учитывая формулу силы тока, имеем для U r:
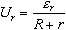
Подставляем значения и проводим расчеты I, U, U r:
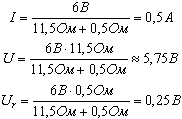
Ответ: сила тока в цепи равна 0,5 А; напряжение на зажимах батареи 5,75 В; падение напряжения на внутреннем сопротивлении 0,25В
Колебание волны:
| СНОВНЫЕ ПОЛОЖЕНИЯ, ЗАКОНЫ И ФОРМУЛЫ |
| Колебания и волны |
| Гармоническое колебание |
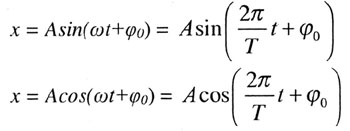
|
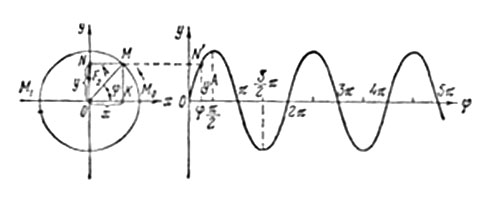
| Фаза колебаний |
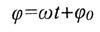
|
|
| Рис. 55 |
| Частота колебаний |
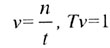
|
| Циклическая частота |
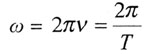
|
| Максимальное ускорение |
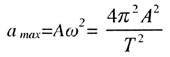
|
| Скорость гармонического колебания |
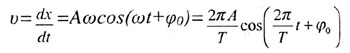
|
| Максимальная скорость |
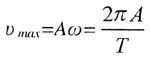
|
| Ускорение колеблющейся точки |
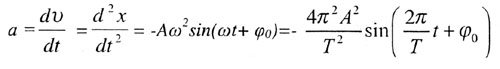
|
| Сила, под действием которой точка массы/и совершает гармоническое колебание |
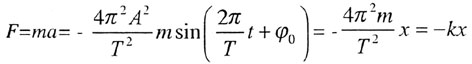
|
| Период колебаний математического маятника |
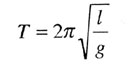
|
| Период колебаний пружинного маятника |
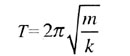
|
| Возвращающая сила |
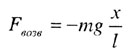
|
| При малых амплитудах период и частота колебаний математического маятника не зависят от амплитуды. |
| Период и частота гармонических колебаний математического маятника не зависят от его массы. |
| Если колебательная система выведена из положения равновесия и затем предоставлена сама себе, то она совершает колебания, называемые свободными колебаниями. |
| Механический резонанс - явление резкого возрастания амплитуды колебаний при совпадении частоты собственных колебаний с частотой периодически действующей вынуждающей силы. |
| Если свободные механические колебания происходят без потерь энергии, то они называются собственными колебаниями. |
| Вынужденными называются колебания, происходящие под действием периодической вынуждающей силы. |
| Потенциальная энергия упруго деформированного тела |
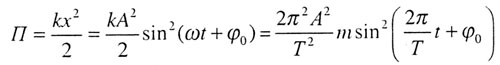
|
| Кинетическая энергия колеблющейся точки |
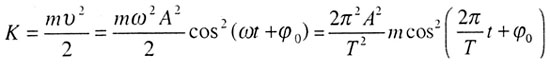
|
| Волной называется процесс распространения колебаний. |
| Продольными называются волны, частицы которых колеблются вдоль направления распространения волны. |
| Звуковой волной называется процесс распространения колебаний упругой среды в диапазоне частот от 16 до 20000 Гц. |
| Поперечными называются волны, частицы которых колеблются перпендикулярно направлению распространения волны. |
| Колебания упругой среды с частотой, большей слышимых частот, называются ультразвуковыми колебаниями, или ультразвуком. |
| Колебания упругой среды с частотой, меньшей слышимых частот, называются инфразвуковыми колебаниями, или инфразвуком. |
| Уравнение гармонической волны |
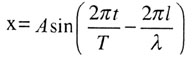
|
| Длина волны |
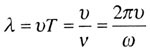
|
| Разность фаз |
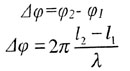
|
| Полная энергия колебаний |
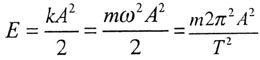
|
| Формула Томсона |
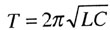
|
| Циклическая частота |
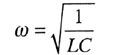
|
| Колебательный контур - электрическая цепь, состоящая из катушки индуктивности L и конденсатора С. |
| В колебательном контуре возникают колебания с одной и той же циклической частотой щ: |
| · заряда q на обкладках конденсатора; · напряжения U на обкладках конденсатора; · силы тока в колебательном контуре; · энергии электрического и магнитного поля. |
| Колебания заряда на обкладках конденсатора |
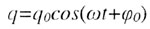
|
| Колебания напряжения |
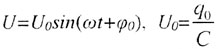
|
| Колебания силы тока |
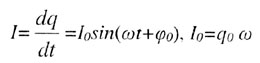
|
| Колебания ЭДС |
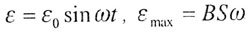
|
| Эффективное (действующее) значение силы тока |
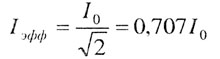
|
| Эффективное (действующее) значение напряжения |
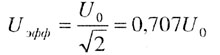
|
| Переменный ток |
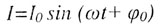
|
| Индуктивное сопротивление |
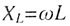
|
| Емкостное сопротивление |
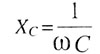
|
| Полное сопротивление цепи переменного тока |
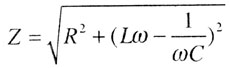
|
| Энергия потерь |
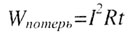
|
| Скорость электромагнитных волн |
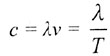
|
| Работа трансформатора |
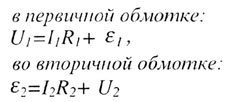
|
| Работа трансформации |
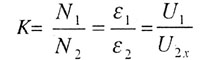
|
| Скорость электромагнитных волн в среде |
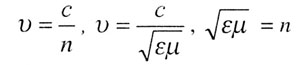
|
Оптика:
ОПТИКА
Свет - это электромагнитные волны, вызывающие зрительное ощущение. Их длина лежит в пределах от 0.4 до 0,8 мкм. Скорость света в вакууме с = 3*108 м/с. Как всякие волны свет огибает препятствия на пути его распространения, испытывая дифракцию (см. ниже). Однако, с увеличением размеров препятствий способность света огибать препятствия уменьшается. В большинстве практических случаев этим явлением можно пренебречь. В таких случаях свет распространяется в виде узких, почти параллельных пучков.
Луч - это направление распространения энергии в световом пучке, т.е. это прямая линия. Чем уже световой пучок, тем точнее он определяет направление луча.
Закон прямолинейного распространения света.
В однородной среде свет распространяется вдоль прямых линий.
Закон отражения света.
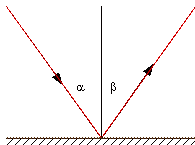
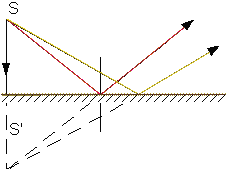
| 
|
| Рис.1. | Рис.2. |
Луч падающий, луч отраженный и перпендикуляр к отражающей поверхности, восставленный в точке падения луча, лежат в одной плоскости, причем угол отражения ( 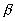 ) равен углу падения (
) равен углу падения ( 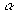 )(рис. 1).
)(рис. 1).
Изображением светящейся точки S в зеркале или линзе называется точка пересечения лучей , вышедших из точки после их отражения в зеркале или преломления в линзе. В зависимости от того, пересекаются ли в точке сами лучи или их продолжения, изображение называютдействительным или мнимым .
Изображение светящейся точки в плоском зеркале мнимо и симметрично самой светящейся точке относительно плоскости зеркала.(Рис.2).
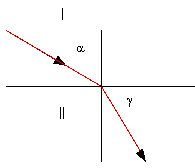
Закон преломления света.
|
| Рис.3. |
Луч падающий, луч преломленный и перпендикуляр к границе раздела двух сред, восставленный в точке падения луча, лежат в одной плоскости; отношение синуса угла падения ( 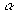 ) к синусу угла преломления (
) к синусу угла преломления ( 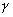 ) есть величина постоянная для данных двух сред (рис. 3):
) есть величина постоянная для данных двух сред (рис. 3):
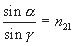 (1)
(1)
Величину п21 называют относительным показателем преломления или показателем преломления второй среды относительно первой.
Абсолютным (табличным) показателем преломления среды называют показатель преломления среды относительно вакуума. (В этом случае на рис. 1 средой I является вакуум).
Относительный показатель преломления п21 связан с абсолютными показателями преломления первой среды п1, второй среды п2 :
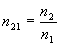 (2)
(2)
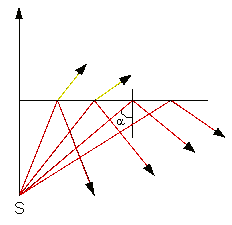
|
| Рис.4. |
Среду с меньшим показателем преломления называют оптически менее плотной. При падении света на границу двух сред со стороны оптически более плотной среды происходит полное отражение, если угол падения больше или равен углу 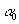 , называемому предельным углом полного отражения (рис.4).
, называемому предельным углом полного отражения (рис.4).
Формально углу 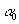 соответствует угол преломления, равный 90°, поэтому:
соответствует угол преломления, равный 90°, поэтому:
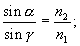 (3)
(3) 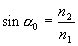 (4)
(4)
Если свет переходит из данной среды (п1= п) в вакуум (п2=1),то :
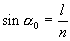 (5)
(5)
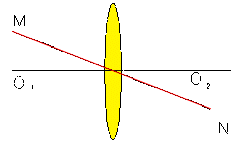
|
| Рис.5. |
Линзой называют прозрачное тело, ограниченное сферическими поверхностями. На рис. 5 О1, О2 - центры сфер ; прямая О1, О2 - главная оптическая ось , точка С -оптический центр линзы; MN- побочная оптическая ось .
| 
| |
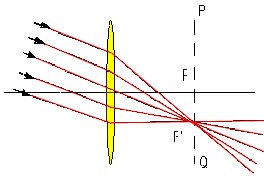
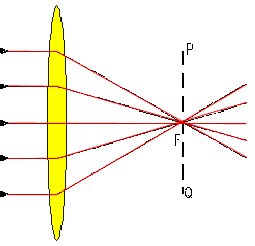
| Рис.6. | Рис.7. |
На рис 6, 7 F - главный фокус линзы; F'- побочный фокус; PQ - фокальная плоскость.
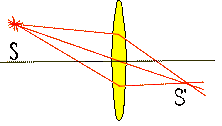
|
| Рис.8. |
Гомоцентрическим называют пучок лучей, пересекающихся в одной точке. Основное свойство линзы: она сохраняет гомоцентричность световых пучков (на рис.8 S - светящаяся точка, S' – её изображение).
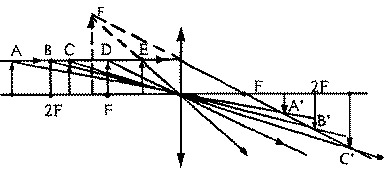
|
| Рис.9. |
На рис.9 дано построение изображения предмета в собирающей линзе при различных его расстояниях от линзы; А ' . - изображение предмета А и т.д. Заметим, что изображения D' нс существует ("уходит в бесконечность"), изображение Е'- мнимое. Формула тонкой линзы:
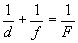 (6)
(6)
где d,f, F- расстояния от линзы соответственно до предмета, до изображения и до главного фокуса. Последнее называют фокусным расстоянием линзы. В формуле линзы все величины берутся со знаком “+”, если соответствующие им точки действительные, и со знаком “-” , если эти точки мнимые.
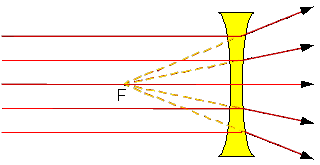
| У рассеивающей линзы фокус мнимый (точка F на рис.10). |
| Рис.10. |
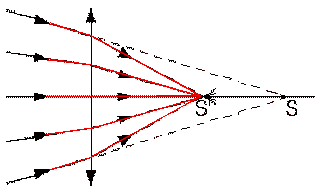
| На рис.11 изображен сходящийся пучок лучей. Точку S можно рассматривать как мнимый источник света, при этом в (6) d<0. |
| Рис.11. |
Оптической силой линзы называют величину, обратную фокусному расстоянию:
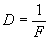 (7)
(7)
Единица оптической силы - диоптрия (дптр). 1 дптр - это оптическая сила линзы с фокусным расстоянием 1 м.
Когерентными называют источники, испускающие колебания в одинаковых фазах или с постоянной разностью фаз.
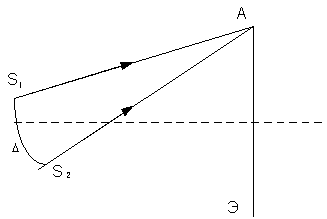
Интерференцией света называют сложение световых пучков, приводящее к образованию устойчивой во времени картины светлых и темных полос. Интерференция света возможна только от когерентных источников.
|
| Рис.12. |
На рис.12 S1, S2 - когерентные источники колебаний, происходящих в одинаковых фазах; 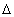 = S2A – S1A - разность хода испускаемых ими волн до точки А экрана. Если колебания придут в точку А в одинаковых фазах, то они усилят друг друга. Это возможно при условии
= S2A – S1A - разность хода испускаемых ими волн до точки А экрана. Если колебания придут в точку А в одинаковых фазах, то они усилят друг друга. Это возможно при условии 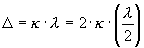 , где
, где 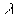 -длина волны. к=0, 1, 2, З... Если колебания придут в точку А в противоположных фазах, то они ослабят друг друга. Это возможно при условии
-длина волны. к=0, 1, 2, З... Если колебания придут в точку А в противоположных фазах, то они ослабят друг друга. Это возможно при условии 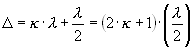 . Для разных точек экрана различны условия интерференции, поэтому на экране Э возникнут чередующиеся светлые и темные полосы.
. Для разных точек экрана различны условия интерференции, поэтому на экране Э возникнут чередующиеся светлые и темные полосы.
Дифракцией света называется огибание световыми волнами препятствий. Дифракция света происходит тем заметнее, чем меньше отношение 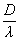 где D - линейные размеры препятствия или отверстия в экране. Поскольку длина волны
где D - линейные размеры препятствия или отверстия в экране. Поскольку длина волны 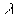 измеряется в долях микрометра (1мкм=10-6 м), то практически дифракция наблюдается лишь при очень малых величинах D. Это осуществляется в дифракционной решетке, представляющей собой совокупность очень узких щелей, разделенных непрозрачными промежутками. Суммарная ширина dпрозрачного и непрозрачного промежутков называется периодом решетки. Если на дифракционную решетку падает нормально к ее поверхности монохроматический (одноцветный) свет с длиной волны
измеряется в долях микрометра (1мкм=10-6 м), то практически дифракция наблюдается лишь при очень малых величинах D. Это осуществляется в дифракционной решетке, представляющей собой совокупность очень узких щелей, разделенных непрозрачными промежутками. Суммарная ширина dпрозрачного и непрозрачного промежутков называется периодом решетки. Если на дифракционную решетку падает нормально к ее поверхности монохроматический (одноцветный) свет с длиной волны 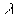 , то в результате явления дифракции на стоящий за решеткой экран лучи пойдут не только прямо, но еще и по направлениям, составляющим углы ±
, то в результате явления дифракции на стоящий за решеткой экран лучи пойдут не только прямо, но еще и по направлениям, составляющим углы ± 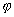 1, ±
1, ± 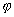 2, ±
2, ± 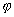 3,......... с первоначальным направлением. Эти углы определяются формулой:
3,......... с первоначальным направлением. Эти углы определяются формулой:
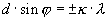 (8)
(8)
где k = 0, 1, 2, 3,...Каждому значению k соответствует по два угла 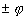 . С помощью (8) можно опытным путем определить длину волны монохроматического света. Наибольшая длина волны (0,8 мкм) соответствует красному цвету, наименьшая - фиолетовому.
. С помощью (8) можно опытным путем определить длину волны монохроматического света. Наибольшая длина волны (0,8 мкм) соответствует красному цвету, наименьшая - фиолетовому.
|
| Рис.13. |
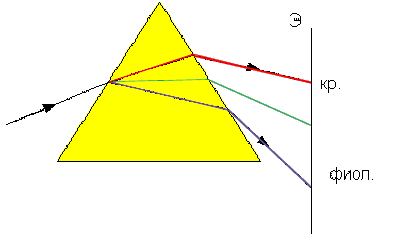
Дисперсией света называется зависимость показателя преломления вещества от цвета падающего на него света. Это проявляется в том, что если направить узкий пучок солнечного света на призму, он выйдет из призмы в виде веера цветных лучей (рис.13). Цвет определяется длиной волны 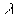 или связанной с ней по формуле
или связанной с ней по формуле 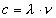 частотой световых колебаний v. С другой стороны, по волновой теории абсолютный показатель преломления вещества равен отношению скорости света в вакууме с = 3*108 м/с к скорости света в веществе v:
частотой световых колебаний v. С другой стороны, по волновой теории абсолютный показатель преломления вещества равен отношению скорости света в вакууме с = 3*108 м/с к скорости света в веществе v: 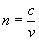 (9)
(9)
Таким образом в основе дисперсии лежит зависимость скорости распространения световых (электромагнитных) колебаний в веществе от их частоты.
Описанный выше солнечный спектр называется непрерывным . Он имеет вид разноцветной полоски, в которой цвета непрерывно переходят один в другой. Сплошные спектры дают все раскаленные твердые или жидкие тела.
Светящиеся газы дают линейчатые спектры. Они представляют собой набор определенным образом расположенных тонких цветных линий, разделенных широкими темными промежутками. Каждому веществу соответствует свой строго определенный набор линий - линейчатый спектр. Это свойство линейчатых спектров лежит в основе спектрального анализа - определения химического состава вещества по его спектру.
Электростатика
Законы постоянного тока
Колебания волны
Оптика
Атомная и ядерная физика
Подготовить к четвергу
Механика:
Кинематика
Основные понятия кинематики
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно (см 1.2) Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.
Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.
В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.
В системе СГС (Сантиметр, грамм, секунда) приняты соответственно сантиметр и секунда.
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела.
Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Колесо обозрения», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.
Понятие материальной точки играет важную роль в механике.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = 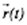 y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени
y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени
радиус-вектора 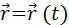 (векторный способ), проведенного из
(векторный способ), проведенного из
начала координат до данной точки (рис. 1.1.1).

Рисунок 1.1.1.
Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t)
и радиус-вектора 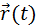
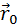 – радиус-вектор положения точки в начальный момент времени
– радиус-вектор положения точки в начальный момент времени
Перемещением тела
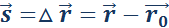
называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.
В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения 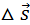 При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).

Рисунок 1.1.2.
Пройденный путь l и вектор перемещения 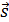 при криволинейном движении тела. a и b – начальная и конечная точки пути при криволинейном движении тела. a и b – начальная и конечная точки пути
|
Для характеристики движения вводится понятие средней скорости:
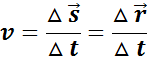
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt,
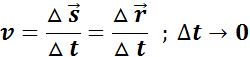
В математике такой предел называют производной и обозначают
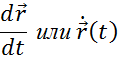
Мгновенная скорость 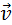 тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.

|
Рисунок 1.1.3.
Средняя и мгновенная скорости.
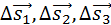 – перемещения за времена – перемещения за времена 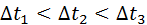 соответственно.
При t→0 соответственно.
При t→0
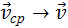
|
При движении тела по криволинейной траектории его скорость 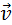 изменяется по модулю и направлению. Изменение вектора скорости
изменяется по модулю и направлению. Изменение вектора скорости 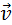 за некоторый малый промежуток времени Δt можно задать с помощью вектора
за некоторый малый промежуток времени Δt можно задать с помощью вектора 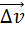 (рис. 1.1.4).
(рис. 1.1.4).
Вектор изменения скорости 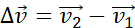 за малое время Δt можно разложить на две составляющие:
за малое время Δt можно разложить на две составляющие: 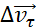 направленную вдоль вектора
направленную вдоль вектора 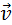 (касательная составляющая), и
(касательная составляющая), и 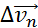 направленную перпендикулярно вектору
направленную перпендикулярно вектору 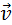 (нормальная составляющая).
(нормальная составляющая).

|
Рисунок 1.1.4.
Изменение вектора скорости по величине и направлению. 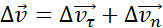 – изменение вектора скорости за время Δt – изменение вектора скорости за время Δt
|
Мгновенным ускорением (или просто ускорением) тела 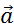 называют предел отношения малого изменения скорости
называют предел отношения малого изменения скорости 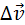 к малому промежутку времени Δt, в течение которого происходило изменение скорости:
к малому промежутку времени Δt, в течение которого происходило изменение скорости:
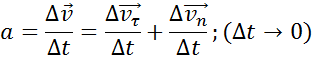
Направление вектора ускорения 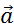 в случае криволинейного движения не совпадает с направле
в случае криволинейного движения не совпадает с направле 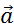 нием вектора
нием вектора 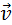 скорости Составляющие вектора ускорения называют касательным(тангенциальным)
скорости Составляющие вектора ускорения называют касательным(тангенциальным) 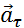 и нормальным
и нормальным 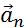 ускорениями (рис. 1.1.5).
ускорениями (рис. 1.1.5).

|
| Рисунок 1.1.5. Касательное и нормальное ускорения |
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:
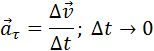
Вектор 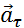 направлен по касательной к траектории.
направлен по касательной к траектории.
Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

|
| Рисунок 1.1.6. Движение по дугам окружностей |
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент: 
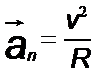
(Эта формула сделана в Mathtype)
Вектор 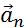 всегда направлен к центру окружности.
всегда направлен к центру окружности.
Из рис. 1.1.5 видно, что модуль полного ускорения равен
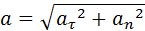
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение 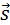 , скорость
, скорость 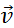 и ускорение
и ускорение 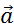 . Путь l является скалярной величиной. Перемещение
. Путь l является скалярной величиной. Перемещение 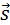 , скорость
, скорость 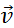 и ускорение
и ускорение 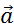 – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
– величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
2. Динамика
Основы динамики
Если в кинематике только описывается движение тел, то в динамике изучаются причины этого движения под действием сил, действующих на тело.
Динамика – раздел механики, который изучает взаимодействия тел, причины возникновения движения и тип возникающего движения. Взаимодействие – процесс, в ходе которого тела оказывают взаимное действие друг на друга. В физике все взаимодействия обязательно парные. Это значит, что тела взаимодействуют друг с другом парами. То есть всякое действие обязательно порождает противодействие.
Сила – это количественная мера интенсивности взаимодействия тел. Сила является причиной изменения скорости тела целиком или его частей (деформации). Сила является векторной величиной. Прямая, вдоль которой направлена сила, называется линией действия силы. Сила характеризуется тремя параметрами: точкой приложения, модулем (численным значением) и направлением. В Международной системе единиц (СИ) сила измеряется в Ньютонах (Н). Для измерения сил используют откалиброванные пружины. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра.
Сила, оказывающая на тело такое же действие, как и все силы, действующие на него, вместе взятые, называется равнодействующей силой. Она равна векторной сумма всех сил, действующих на тело:
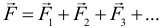
Чтобы найти векторную сумму нескольких сил нужно выполнить чертеж, где правильно нарисовать все силы и их векторную сумму, и по данному чертежу с использованием знаний из геометрии (в основном это теорема Пифагора и теорема косинусов) найти длину результирующего вектора.
Виды сил:
Сила тяжести. Приложена к центру масс тела и направлена вертикально вниз (или что тоже самое: перпендикулярно линии горизонта), и равна:
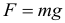
где: g - ускорение свободного падения, m - масса тела. Не перепутайте: сила тяжести перпендикулярна именно горизонту, а не поверхности на которой лежит тело. Таким образом, если тело лежит на наклонной поверхности, сила тяжести по-прежнему будет направлена строго вниз.
Сила трения. Приложена к поверхности соприкосновения тела с опорой и направлена по касательной к ней в сторону противоположную той, куда тянут, или пытаются тянуть тело другие силы.
Сила вязкого трения (сила сопротивления среды). Возникает при движении тела в жидкости или газе и направлена против скорости движения.
Сила реакции опоры. Действует на тело со стороны опоры и направлена перпендикулярно опоре от нее. Когда тело опирается на угол, то сила реакции опоры направлена перпендикулярно поверхности тела.
Сила натяжения нити. Направлена вдоль нити от тела.
Сила упругости. Возникает при деформации тела и направлена против деформации.
Обратите внимание и отметьте для себя очевидный факт: если тело находится в покое, то равнодействующая сил равна нулю.
Закон сохранения
Кинетическая энергия тела массой m, движущегося со скоростью  :
:
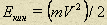 .
.
Потенциальная энергия тела массой m, находящегося на высоте h, в поле сил тяжести с ускорением свободного падения 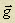 :
:
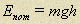 .
.
Энергия пружины с коэффициентом жесткости k, сжатой или растянутой на 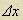 :
:
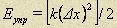 .
.
Импульс тела массой m, движущегося со скоростью  :
:
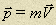 .
.
Закон сохранения энергии:
В замкнутых системах полная энергия (потенциальная + кинетическая + тепловая) системы тел сохраняется.
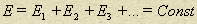 .
.
Если при этом можно пренебречь переходом механической энергии (потенциальная + кинетическая) в тепловую, то сохраняется механическая энергия системы.
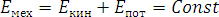
Абсолютно упругим ударом называется такое кратковременное взаимодействие тел, после которого тела полностью восстанавливают свою форму, а их суммарная кинетическая энергия не изменяется. При абсолютно упругом ударе выполняются закон сохранения импульса и закон сохранения механической энергии.
Абсолютно неупругим ударом называется такое кратковременное взаимодействие тел, после которого соударяющиеся тела образуют единое тело, движущееся с определенной скоростью, а суммарная кинетическая энергия тел уменьшается. При абсолютно неупругом ударе выполняется закон сохранения импульса, а механическая энергия не сохраняется, часть ее превращается во внутреннюю энергию тел.
Закон сохранения импульса:
Полный импульс замкнутой системы тел остается постоянным.
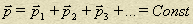 .
.
Работа постоянной силы 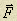 :
:
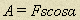 ,
,
где s – модуль перемещения, 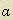 - угол между векторами силы
- угол между векторами силы 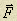 и перемещения
и перемещения  .
.
Работа так же может быть найдена по следующей формуле:
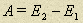 .
.
Мощность – работа A совершенная за единицу времени:
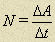 .
.
Силы:
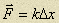 - сила упругости.
- сила упругости.
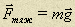 - сила тяжести.
- сила тяжести.
Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).
Первый закон Ньютона. Инерциальные и неинерциальные системы отсчёта Всякому телу свойственно сохранять состояние равномерного прямолинейного движения или покоя, пока и поскольку другие тела не вынудят его изменить это состояние. Указанное свойство тел называется инерцией, инертностью. Первый закон выполняется не во всех системах отсчета, а только в инерциальных. Так что, по существу, первый закон постулирует существование инерциальных систем отсчёта, то есть таких, где выполняется закон инерции. По этому закону, существует хотя бы одна инерциальная система отсчёта, а следовательно, их бесконечное число: любая система отсчёта, движущаяся относительно инерциальной с постоянной скоростью ( 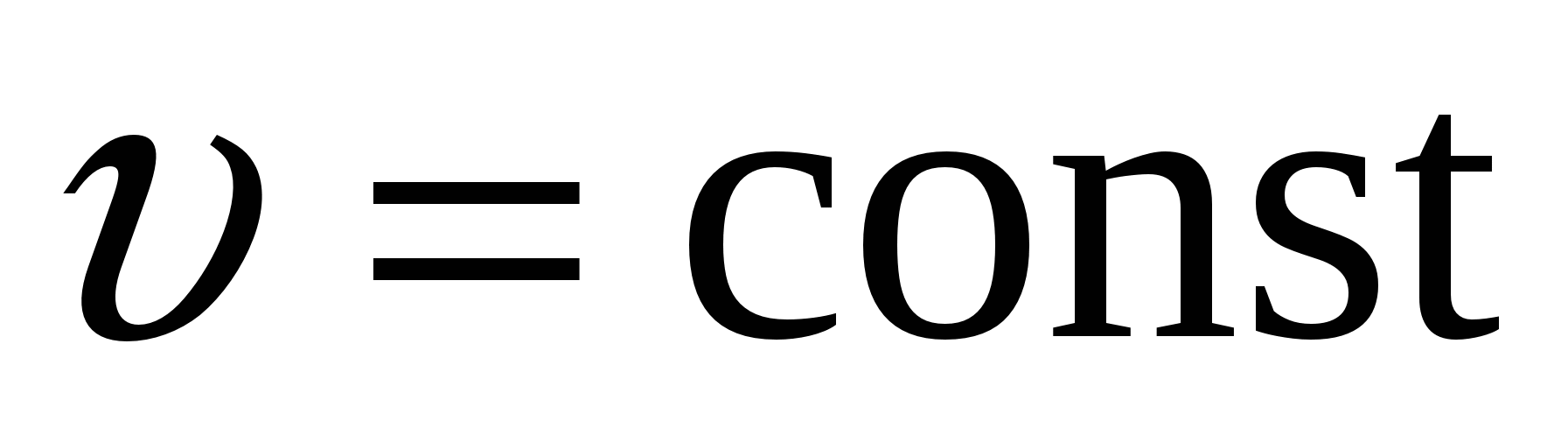 ), также является инерциальной. Неинерциальных систем отсчёта тоже бесконечно много: это – любая, движущаяся ускоренно относительно какой-либо инерциальной. 3. Второй закон Ньютона. Импульс тела, импульс силы В результате взаимодействия с другими телами тело может получить ускорение
), также является инерциальной. Неинерциальных систем отсчёта тоже бесконечно много: это – любая, движущаяся ускоренно относительно какой-либо инерциальной. 3. Второй закон Ньютона. Импульс тела, импульс силы В результате взаимодействия с другими телами тело может получить ускорение  . Одинаковое по величине воздействие разным телам сообщает разные ускорения: чем больше инертность тела, тем меньше ускорение. Количественной мерой инертности тела является масса
. Одинаковое по величине воздействие разным телам сообщает разные ускорения: чем больше инертность тела, тем меньше ускорение. Количественной мерой инертности тела является масса 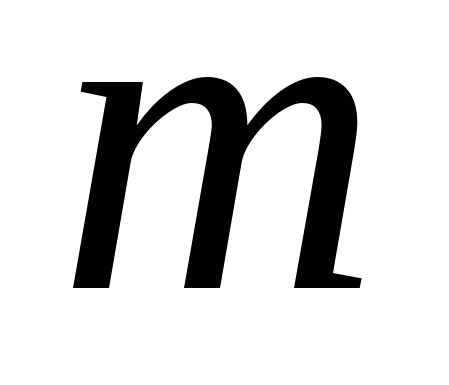 . Размерность массы в системе единиц СИ –
. Размерность массы в системе единиц СИ – 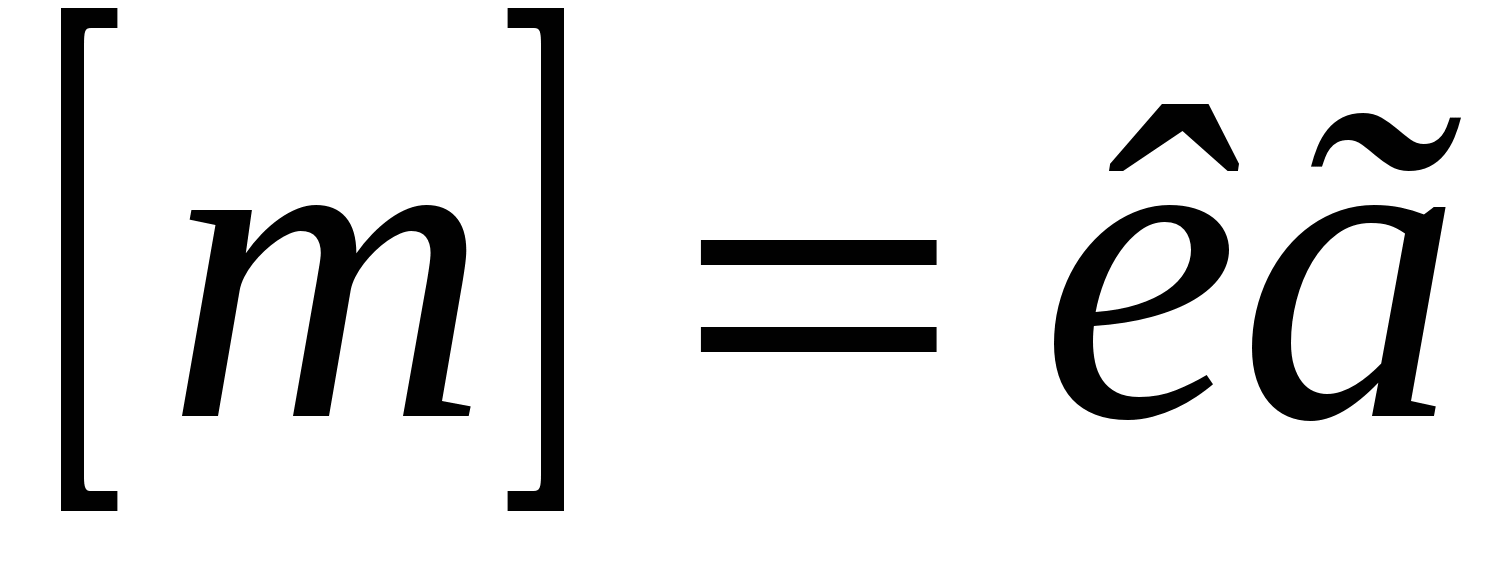 Сила – количественная мера воздействия одного тела на другое. Она характеризуется величиной, направлением и точкой приложения. Сила – вектор:
Сила – количественная мера воздействия одного тела на другое. Она характеризуется величиной, направлением и точкой приложения. Сила – вектор: 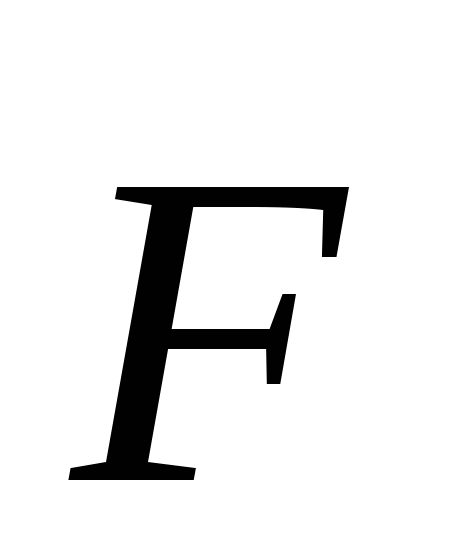 . Размерность силы – ньютон:
. Размерность силы – ньютон: 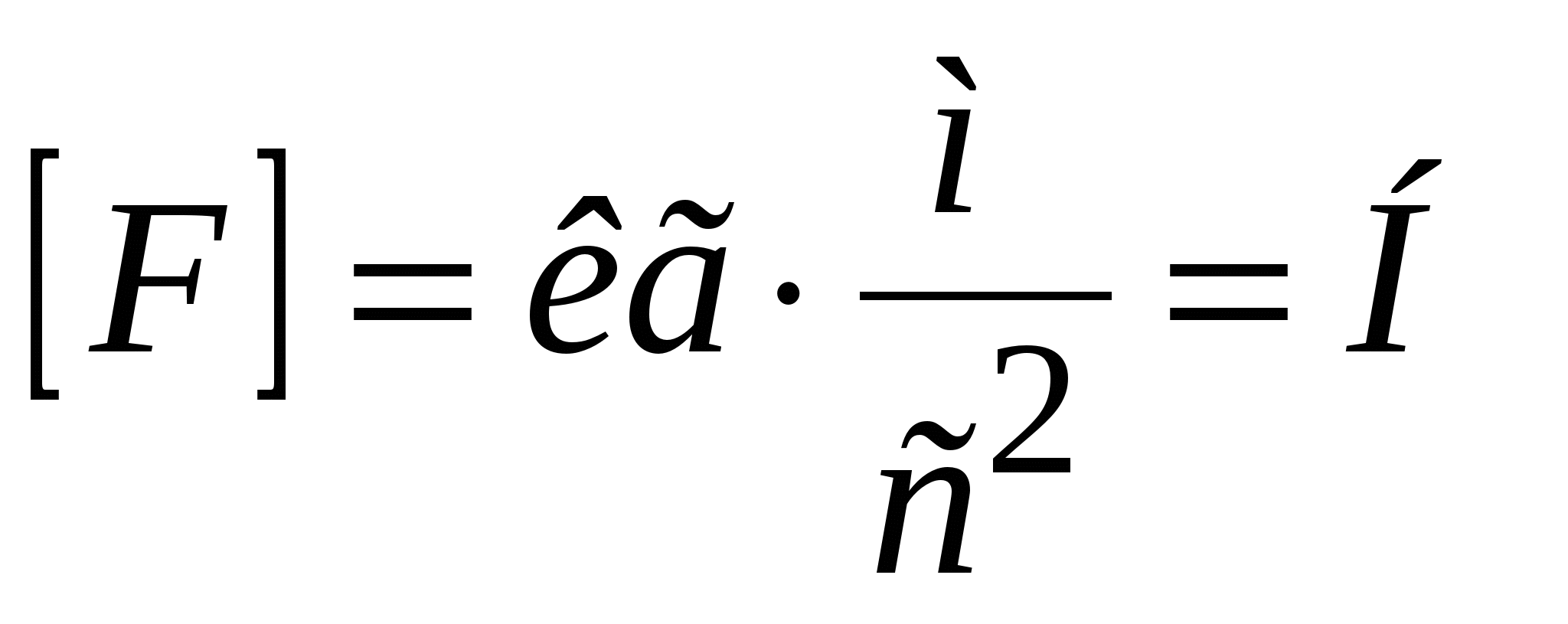 . Формулировка второго закона Ньютона: ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально массе тела
. Формулировка второго закона Ньютона: ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально массе тела 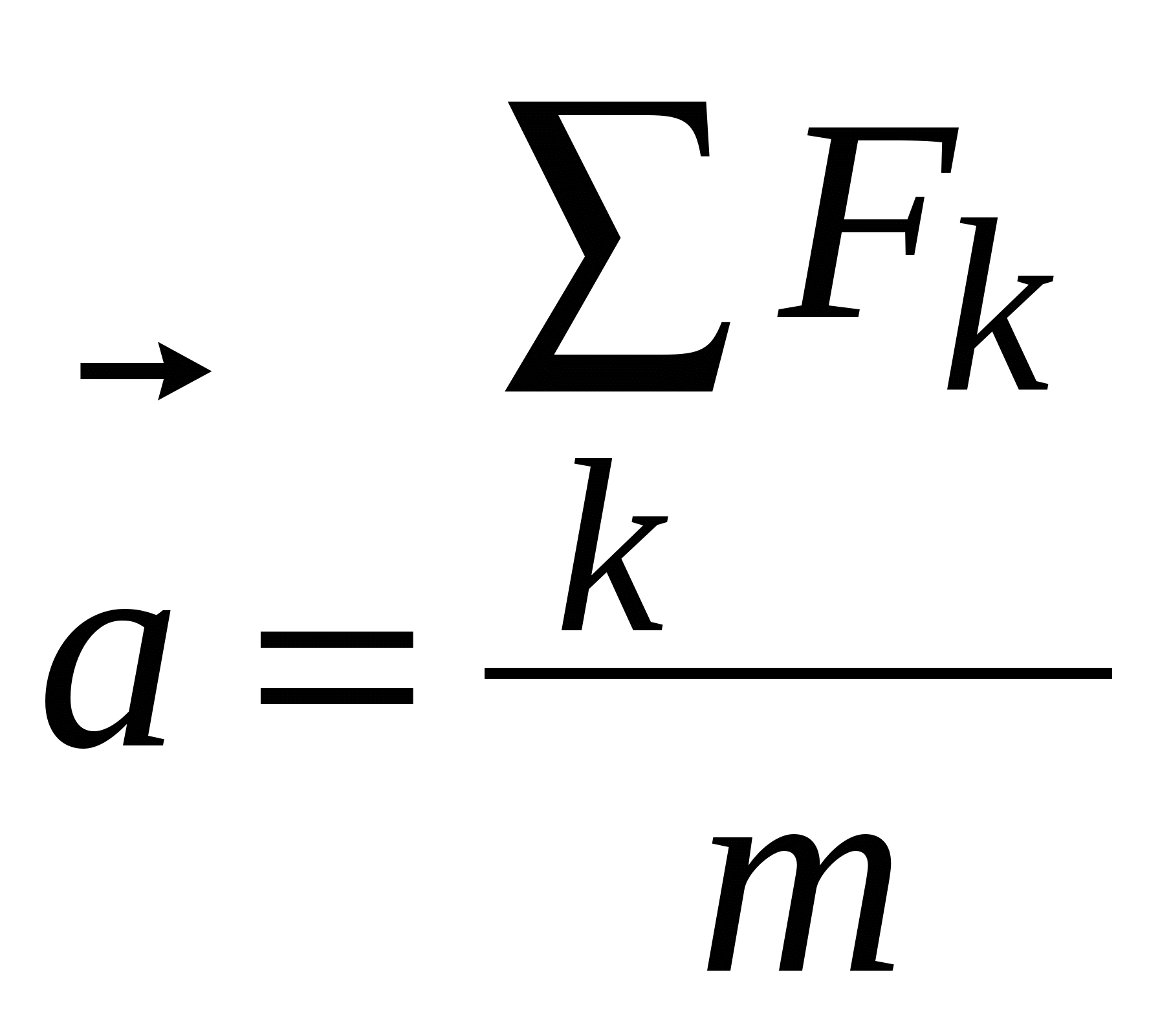 . (2.1) Напоминаем, что это – закон, полученный при обобщении опытных данных; он не доказывается. В числителе стоит равнодействующая всех сил, приложенных к телу, то есть их векторная сумма:
. (2.1) Напоминаем, что это – закон, полученный при обобщении опытных данных; он не доказывается. В числителе стоит равнодействующая всех сил, приложенных к телу, то есть их векторная сумма: 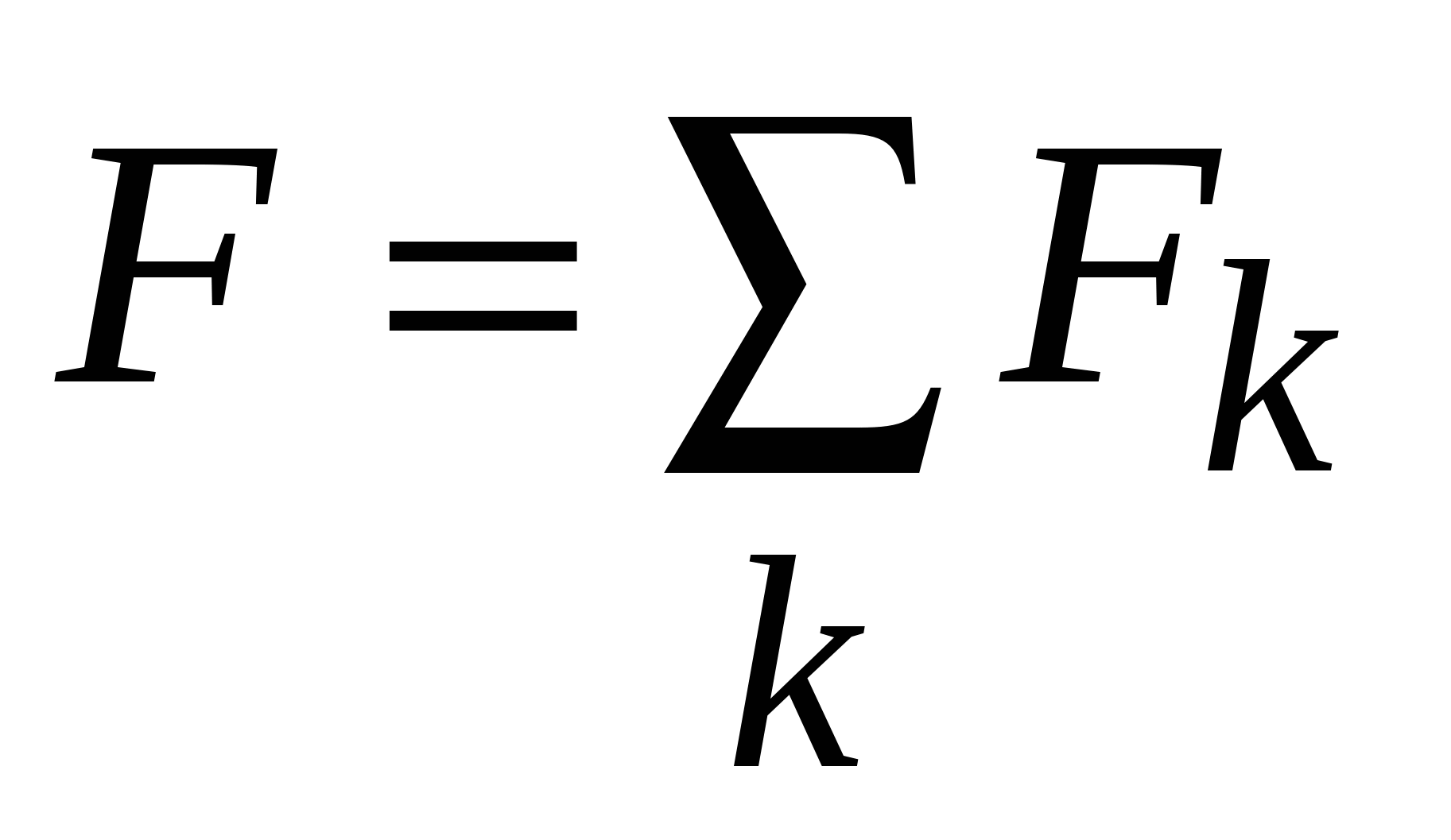 ; – её действие эквивалентно совместному действию всех реально приложенных к телу сил. По определению (см.лекцию 1) ускорение тела
; – её действие эквивалентно совместному действию всех реально приложенных к телу сил. По определению (см.лекцию 1) ускорение тела 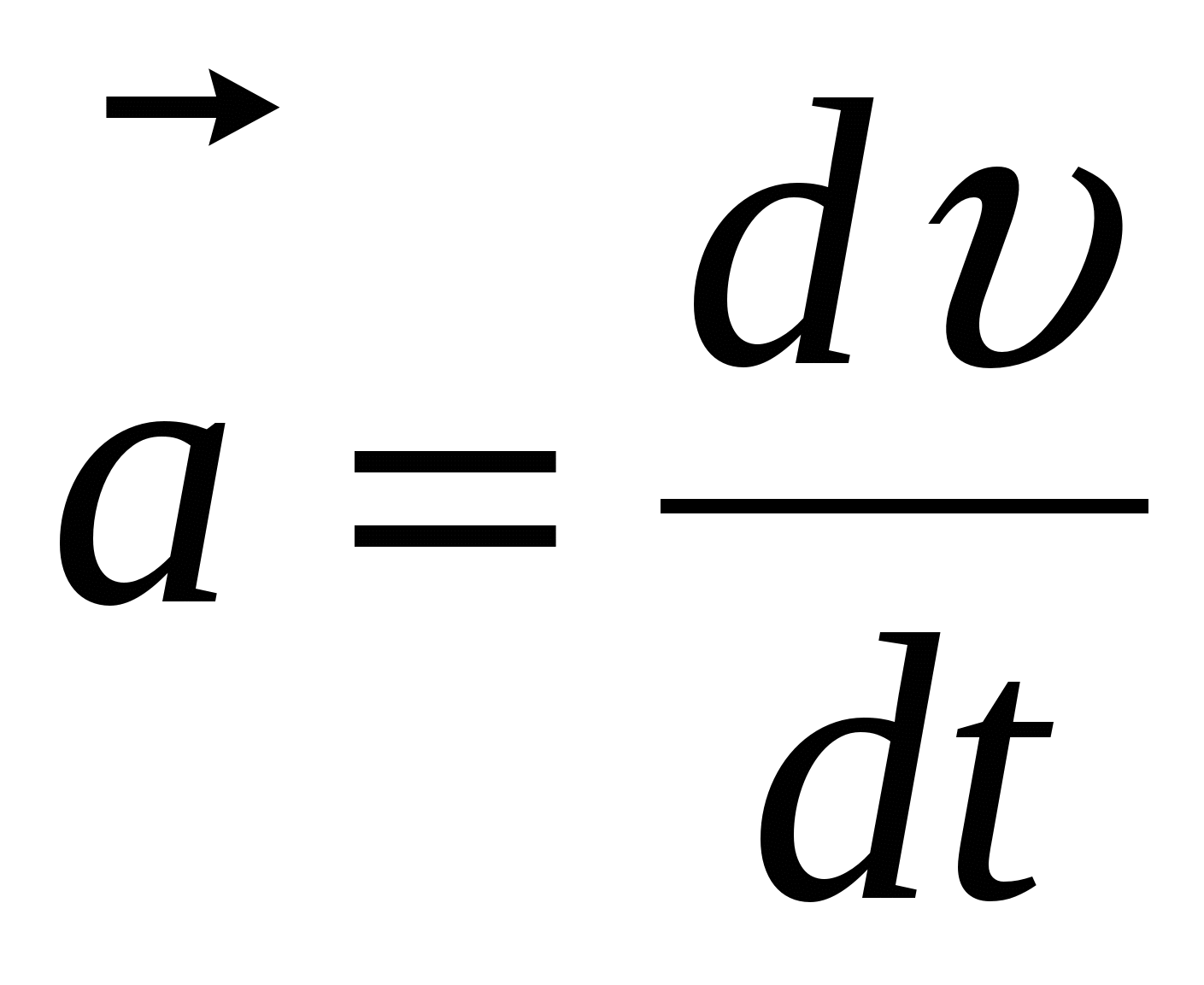 , тогда:
, тогда: 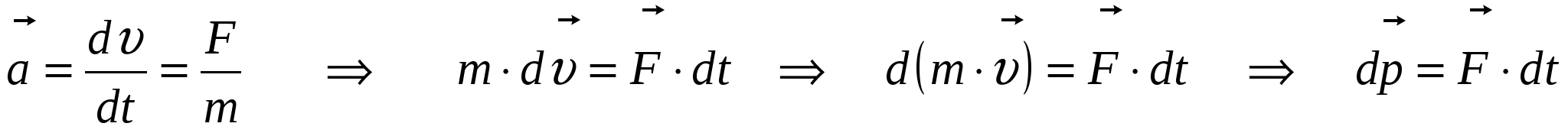 . Интегрируем последнее равенство:
. Интегрируем последнее равенство: 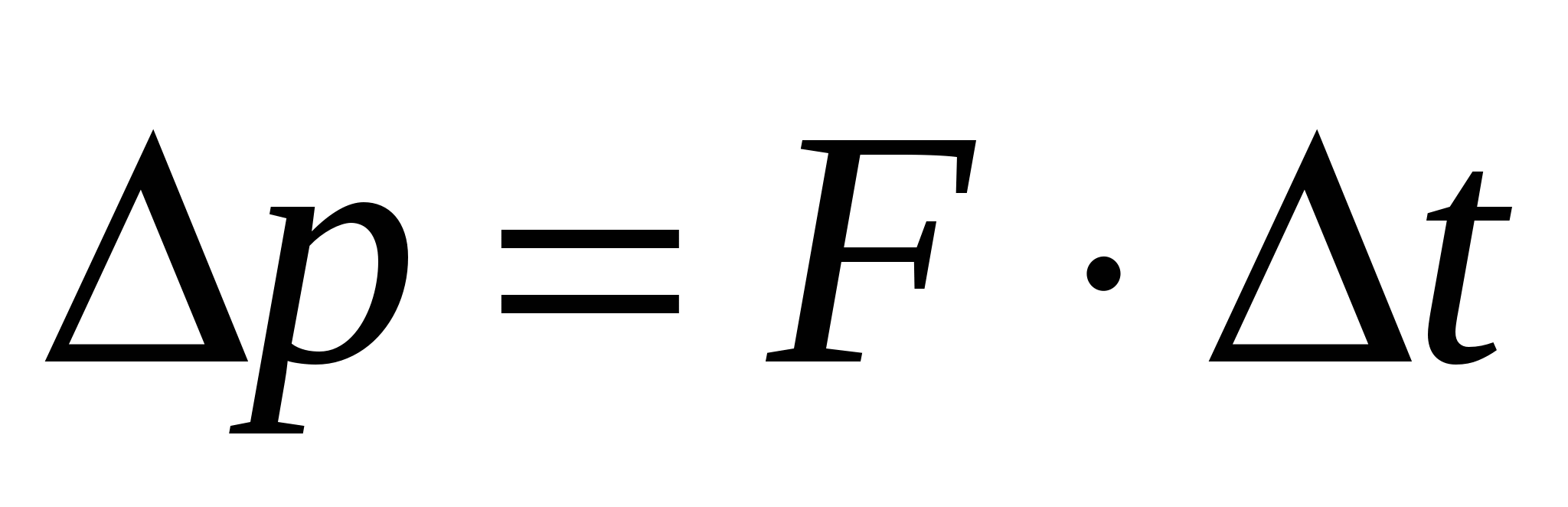 . (2.2) Это – второй закон Ньютона в импульсной форме: изменение импульса тела равно импульсу действовавшей на тело силы. Напоминаем, что произведение силы на промежуток времени, в течение которого она действовала, называется импульсом силы:
. (2.2) Это – второй закон Ньютона в импульсной форме: изменение импульса тела равно импульсу действовавшей на тело силы. Напоминаем, что произведение силы на промежуток времени, в течение которого она действовала, называется импульсом силы: 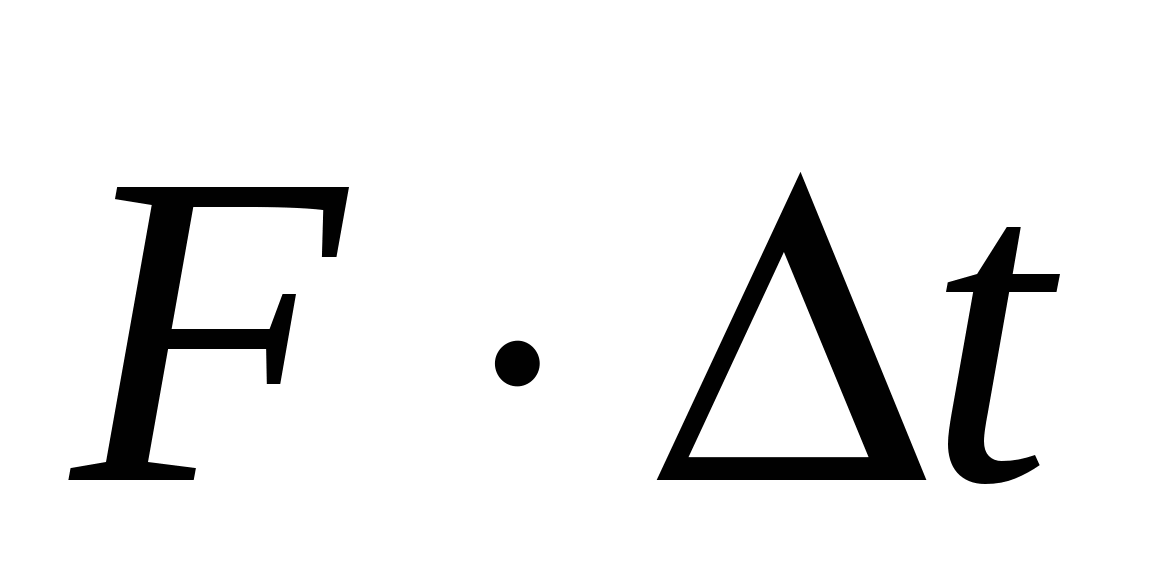 , (2.3) а произведение массы тела на его скорость – импульсом тела:
, (2.3) а произведение массы тела на его скорость – импульсом тела: 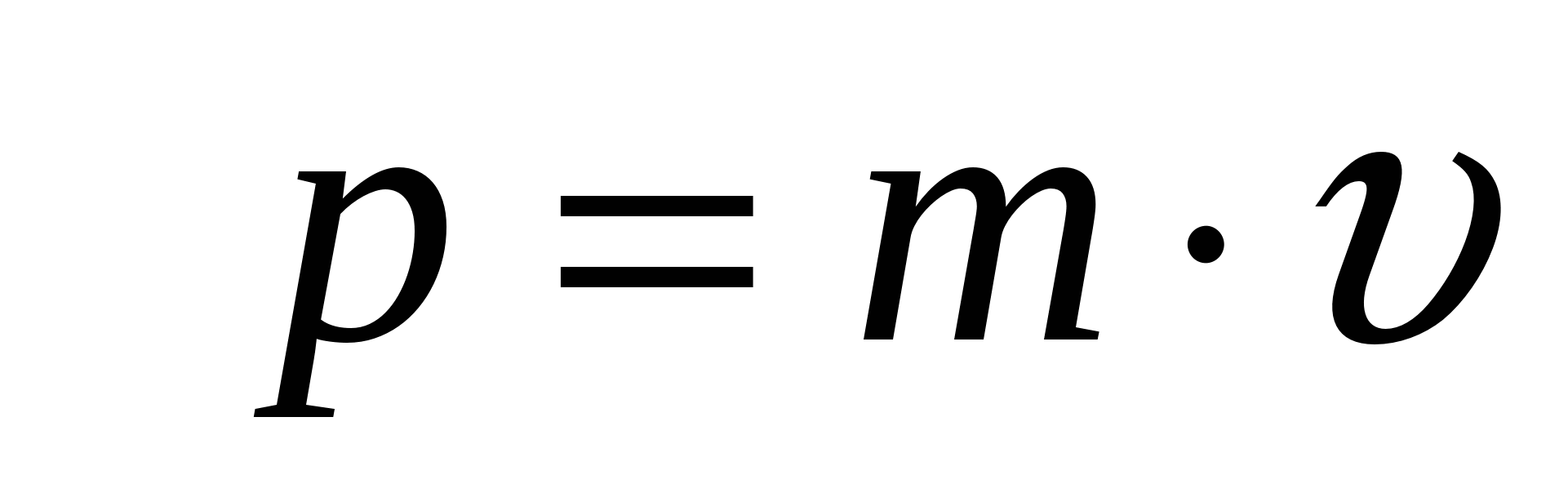 . (2.4) Второй закон Ньютона в виде (2.1) выполняется только при скоростях, много меньше скорости света; а в импульсной форме (2.5) его можно применять и при скоростях, сравнимых со скоростью света:
. (2.4) Второй закон Ньютона в виде (2.1) выполняется только при скоростях, много меньше скорости света; а в импульсной форме (2.5) его можно применять и при скоростях, сравнимых со скоростью света: 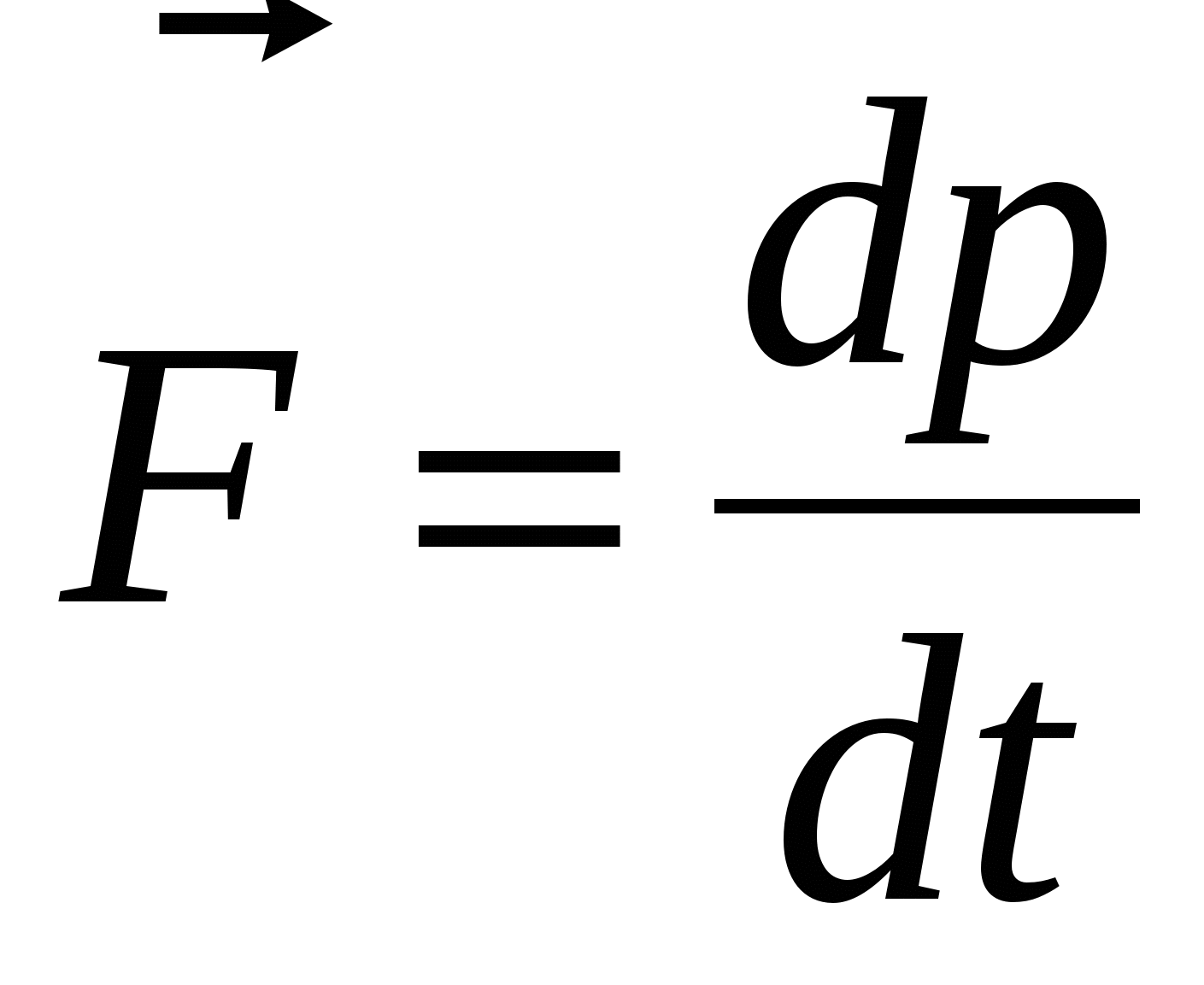 . (2.5) 4 . Третий закон Ньютона Всякое действие тел друг на друга носит характер взаимодействия. Тела действуют друг на друга с силами, равными по величине и направленными вдоль одной прямой в противоположные стороны. Из этого закона следует, что силы всегда появляются парами: если существует сила
. (2.5) 4 . Третий закон Ньютона Всякое действие тел друг на друга носит характер взаимодействия. Тела действуют друг на друга с силами, равными по величине и направленными вдоль одной прямой в противоположные стороны. Из этого закона следует, что силы всегда появляются парами: если существует сила 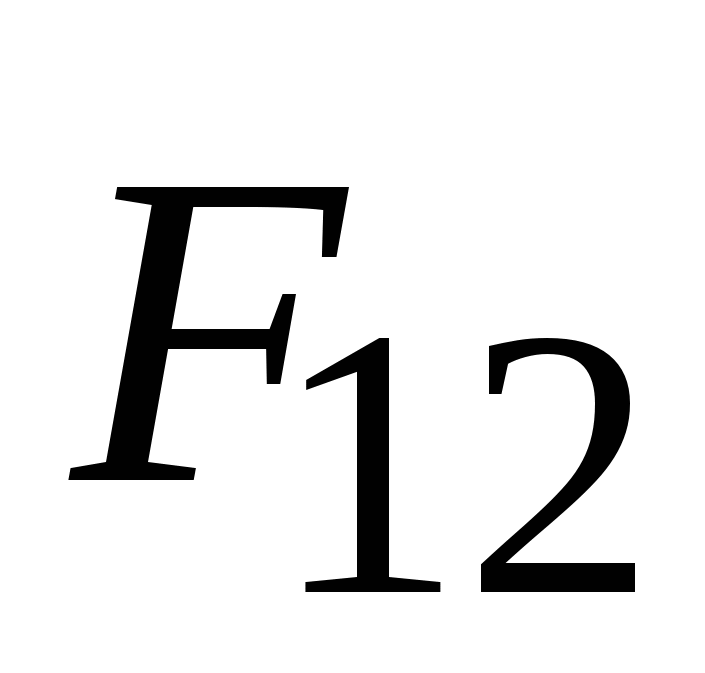 , действующая на тело 1 со стороны тела 2, что и тело 1 действует на тело 2 с силой
, действующая на тело 1 со стороны тела 2, что и тело 1 действует на тело 2 с силой 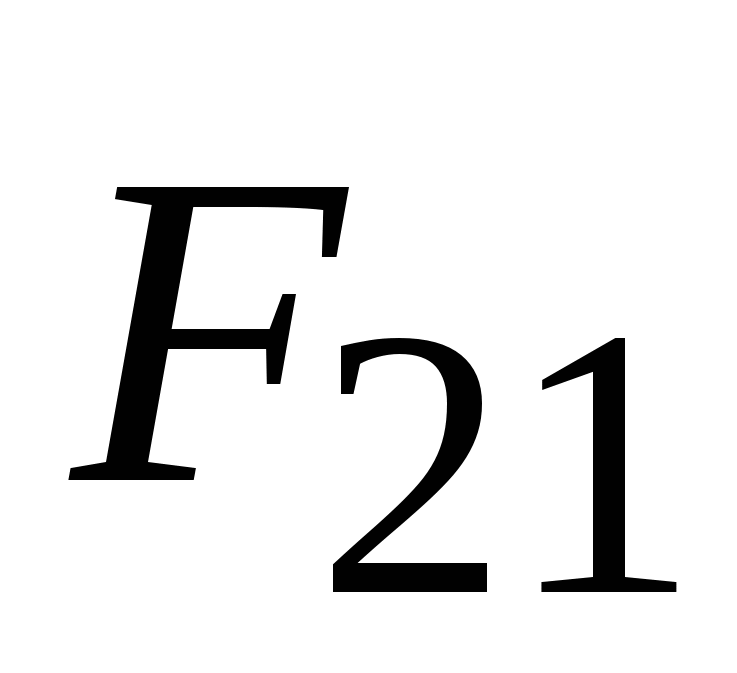 , равной по величине и противоположной по направлению:
, равной по величине и противоположной по направлению: 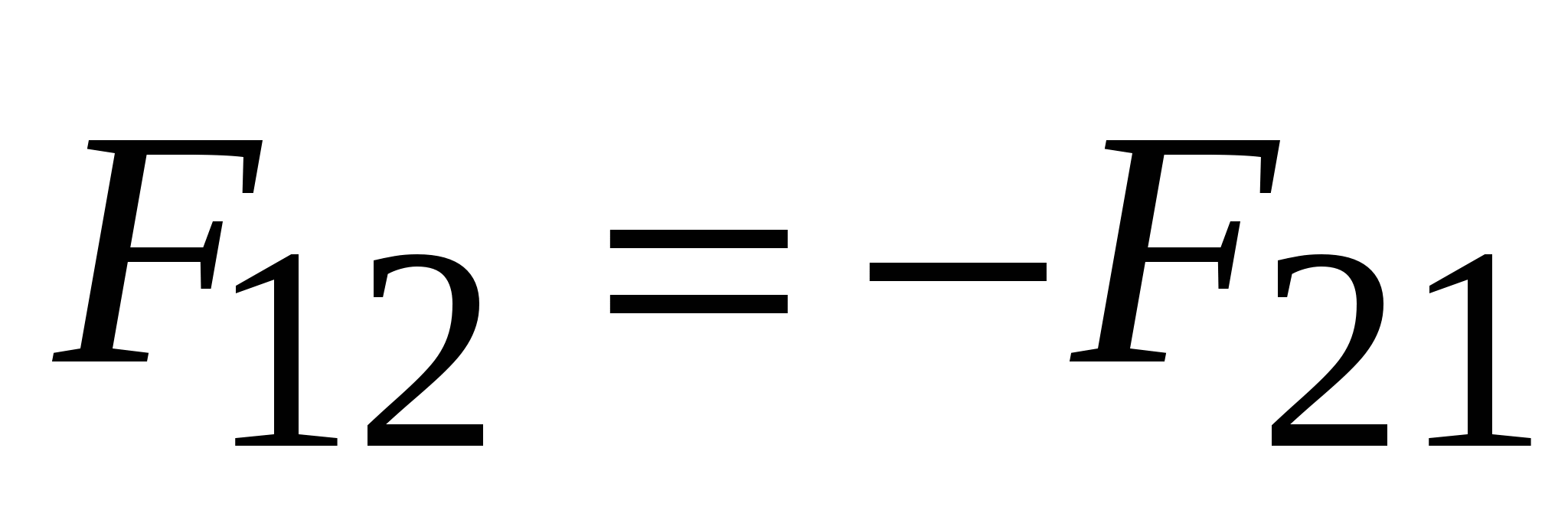 . (2.6) Природа этих сил одинакова. Эти силы не могут компенсировать друг друга, так как приложены к разным телам. В заключение рассмотрения законов Ньютона нужно подчеркнуть, что первый закон Ньютона устанавливает (постулирует) существование инерциальных систем отсчёта, а второй и третий законы Ньютона выполняются именно в таких (инерциальных) системах отсчёта. Сила всемирного тяготения. Закон всемирного тяготения. Сила тяжести, вес тела. Две материальные точки притягиваются друг к другу с силой, прямо пропорциональной каждой массе и обратно пропорциональной квадрату расстояния между точками:
. (2.6) Природа этих сил одинакова. Эти силы не могут компенсировать друг друга, так как приложены к разным телам. В заключение рассмотрения законов Ньютона нужно подчеркнуть, что первый закон Ньютона устанавливает (постулирует) существование инерциальных систем отсчёта, а второй и третий законы Ньютона выполняются именно в таких (инерциальных) системах отсчёта. Сила всемирного тяготения. Закон всемирного тяготения. Сила тяжести, вес тела. Две материальные точки притягиваются друг к другу с силой, прямо пропорциональной каждой массе и обратно пропорциональной квадрату расстояния между точками: 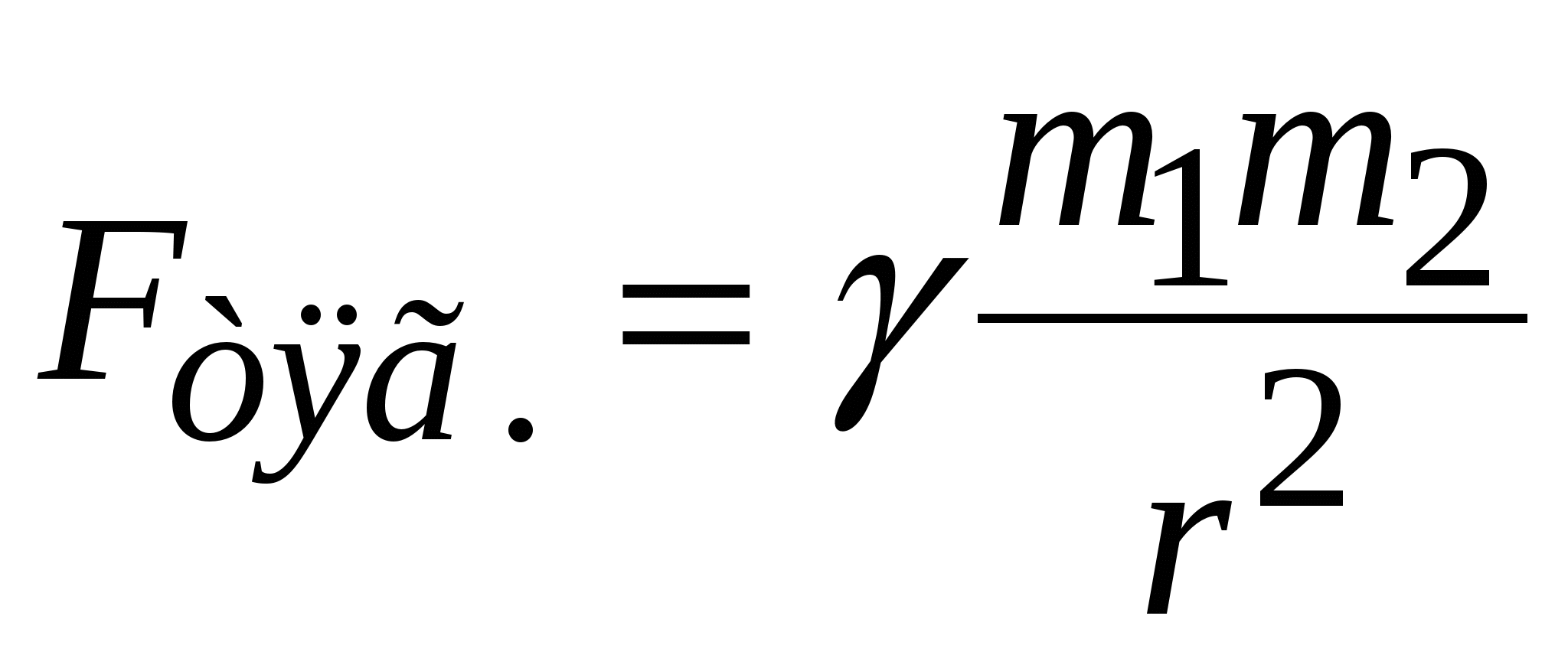 , (2.7) где
, (2.7) где 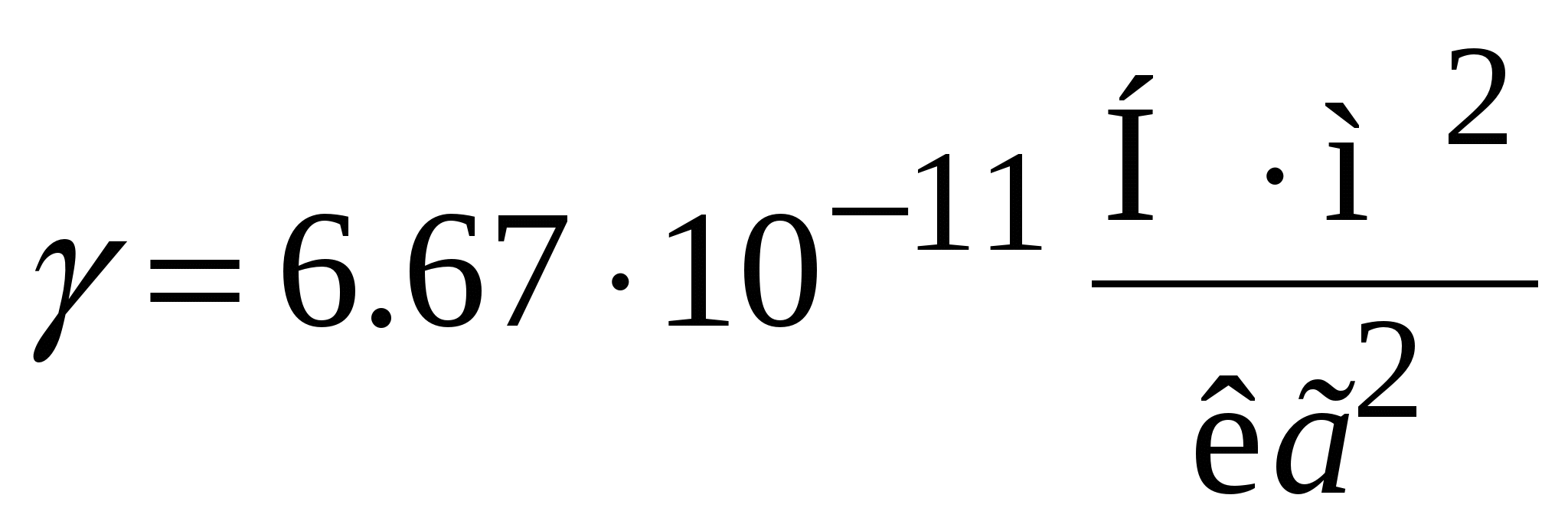 – гравитационная постоянная. Любая масса создаёт в окружающем пространстве гравитационное поле. Поле – это пространство с особым свойством: если в гравитационное поле поместить другую массу, то на неё со стороны поля будет действовать сила. Две массы взаимодействуют посредством гравитационного поля. Для гравитационных полей, как и для любых полей, характерно близкодействие, то есть гравитационное взаимодействие распространяется с конечной скоростью, равной скорости света в вакууме
– гравитационная постоянная. Любая масса создаёт в окружающем пространстве гравитационное поле. Поле – это пространство с особым свойством: если в гравитационное поле поместить другую массу, то на неё со стороны поля будет действовать сила. Две массы взаимодействуют посредством гравитационного поля. Для гравитационных полей, как и для любых полей, характерно близкодействие, то есть гравитационное взаимодействие распространяется с конечной скоростью, равной скорости света в вакууме 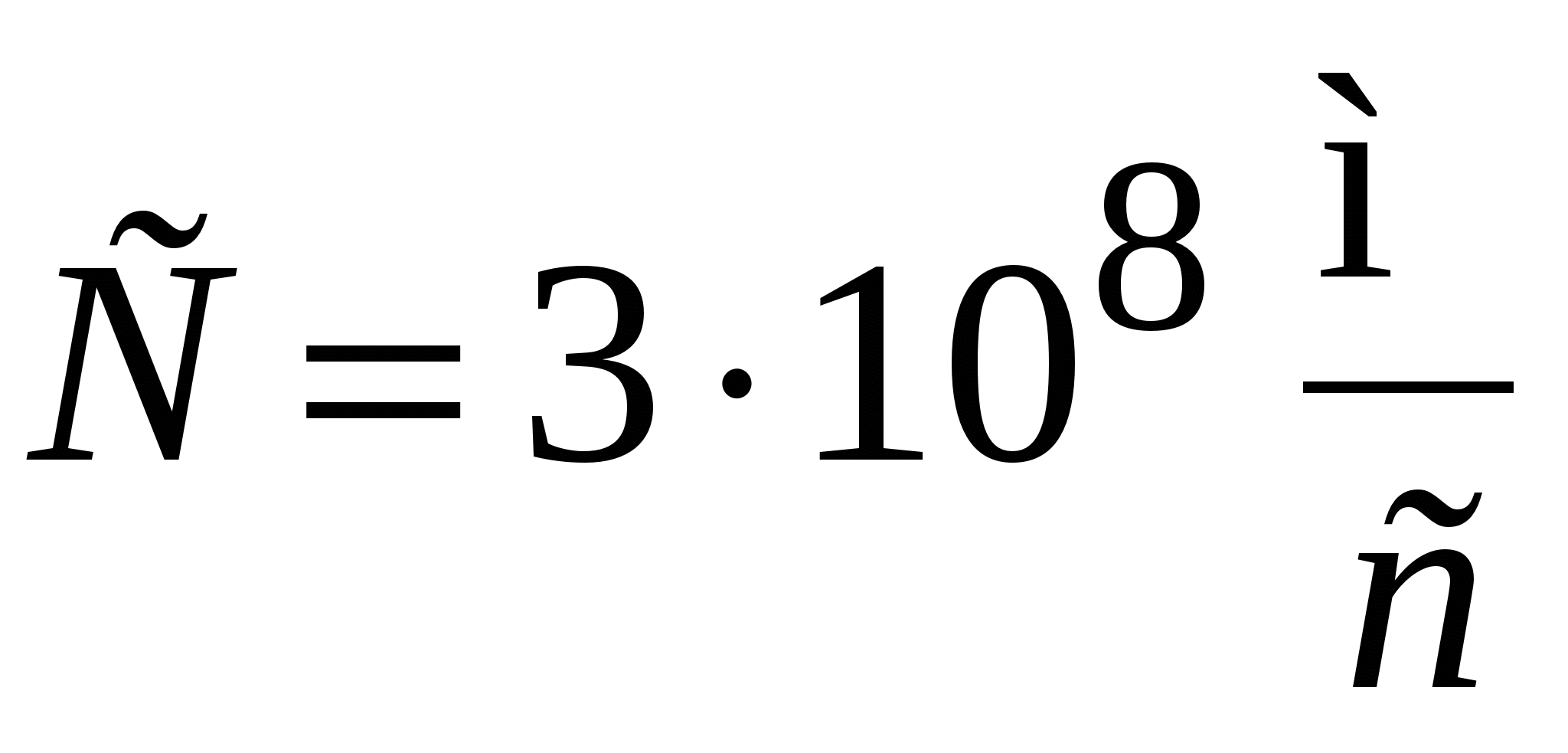 . Вблизи Земли (или другого небесного тела) с массой M, радиусом R тело массой m притягивается к ней с силой:
. Вблизи Земли (или другого небесного тела) с массой M, радиусом R тело массой m притягивается к ней с силой: 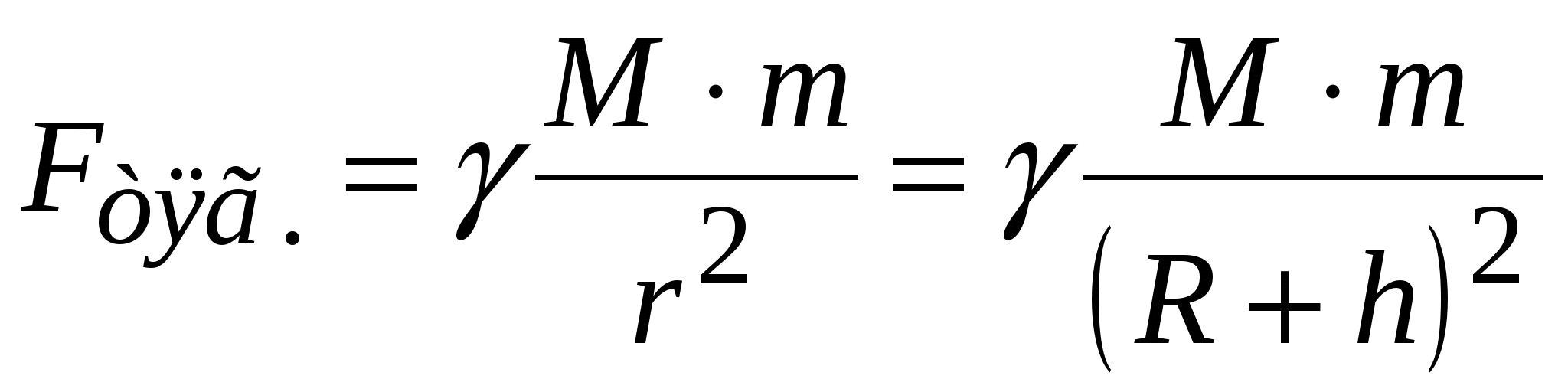 , (2.8) где
, (2.8) где 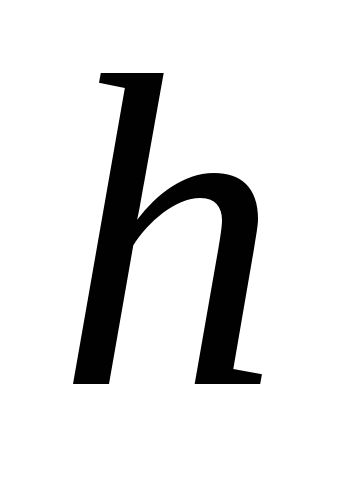 – высота над поверхностью Земли. Это – сила тяжести:
– высота над поверхностью Земли. Это – сила тяжести: 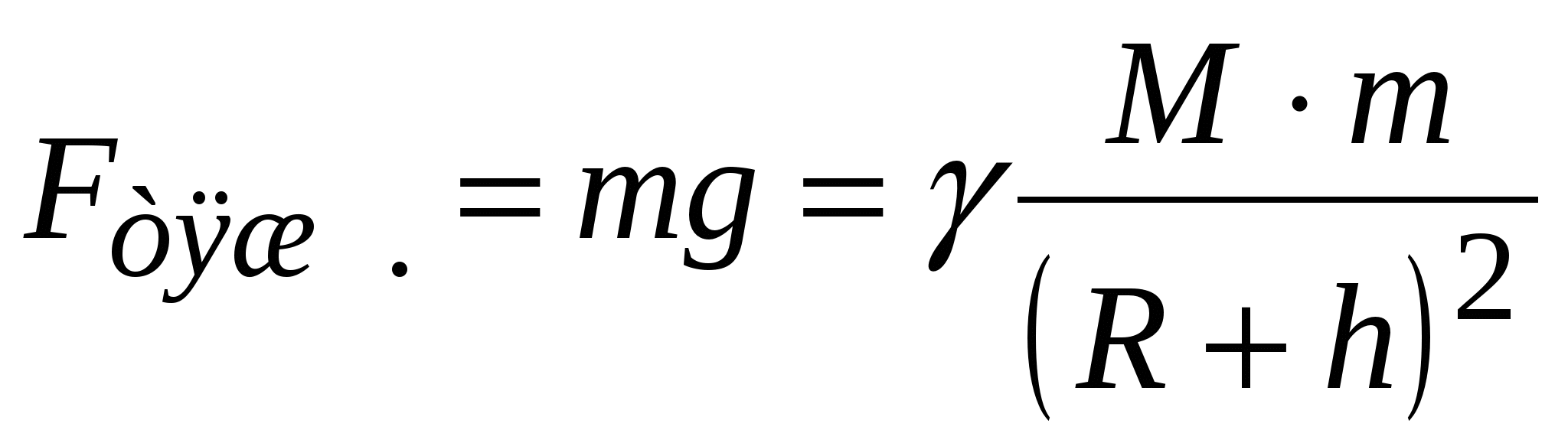 . (2.9) Величина ускорения свободного падения
. (2.9) Величина ускорения свободного падения 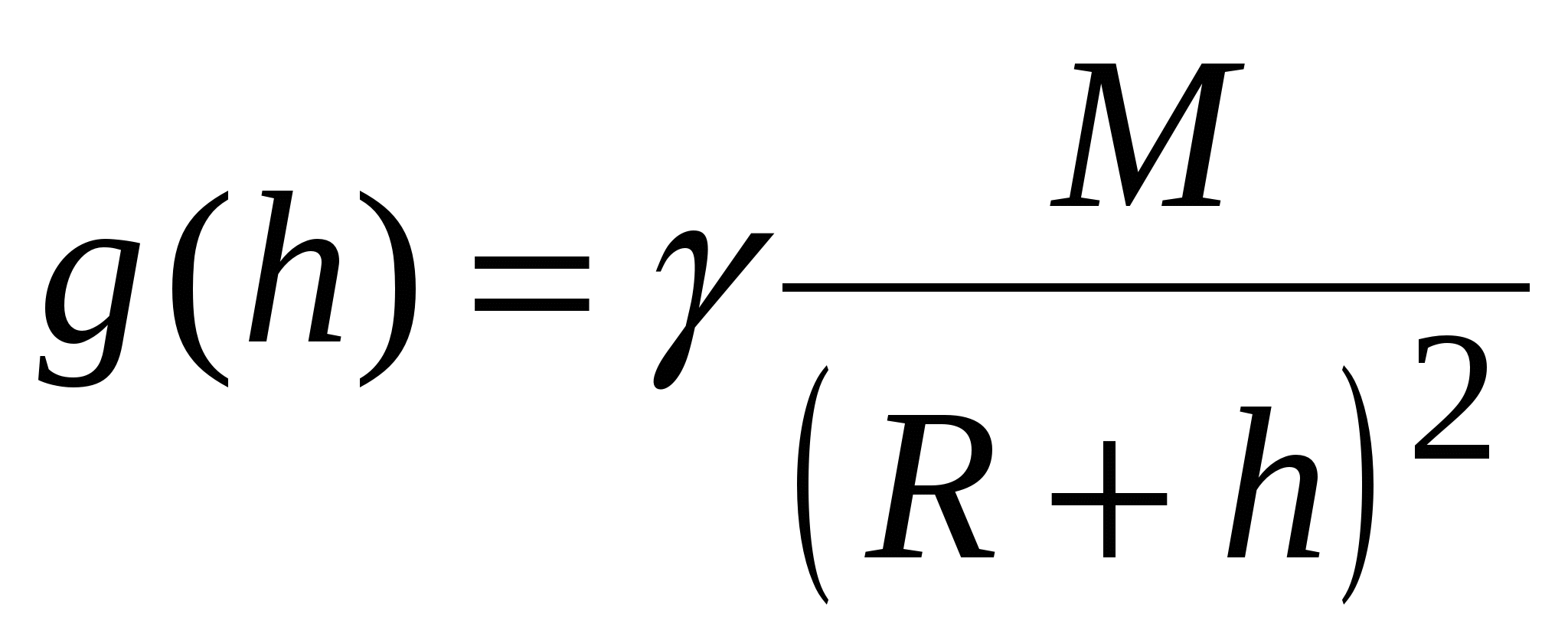 , а на поверхности Земли
, а на поверхности Земли 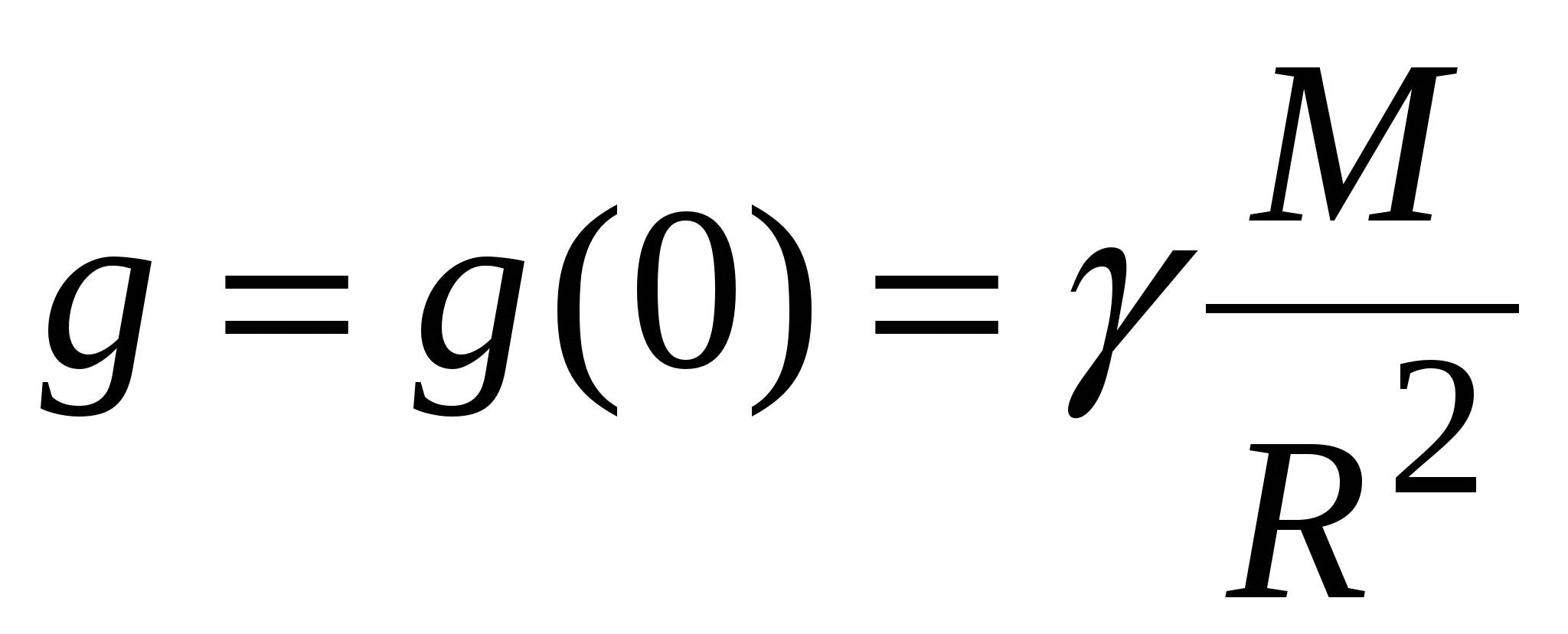 . (2.10) Вес тела
. (2.10) Вес тела 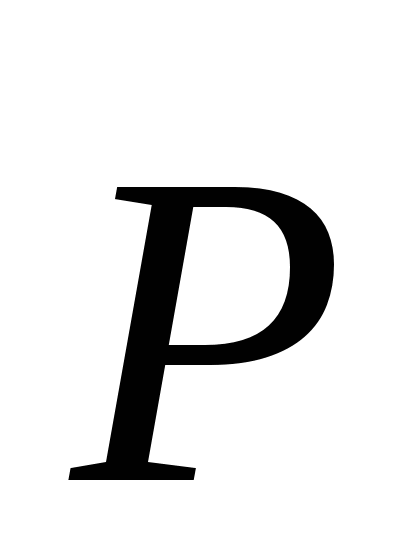 – это сила, с которой тело давит на подставку или растягивает подвес. Вес – сила, приложенная к подставке. Вес по третьему закону Ньютона равен и противоположен силе нормального давления
– это сила, с которой тело давит на подставку или растягивает подвес. Вес – сила, приложенная к подставке. Вес по третьему закону Ньютона равен и противоположен силе нормального давления  (или натяжения нити):
(или натяжения нити): 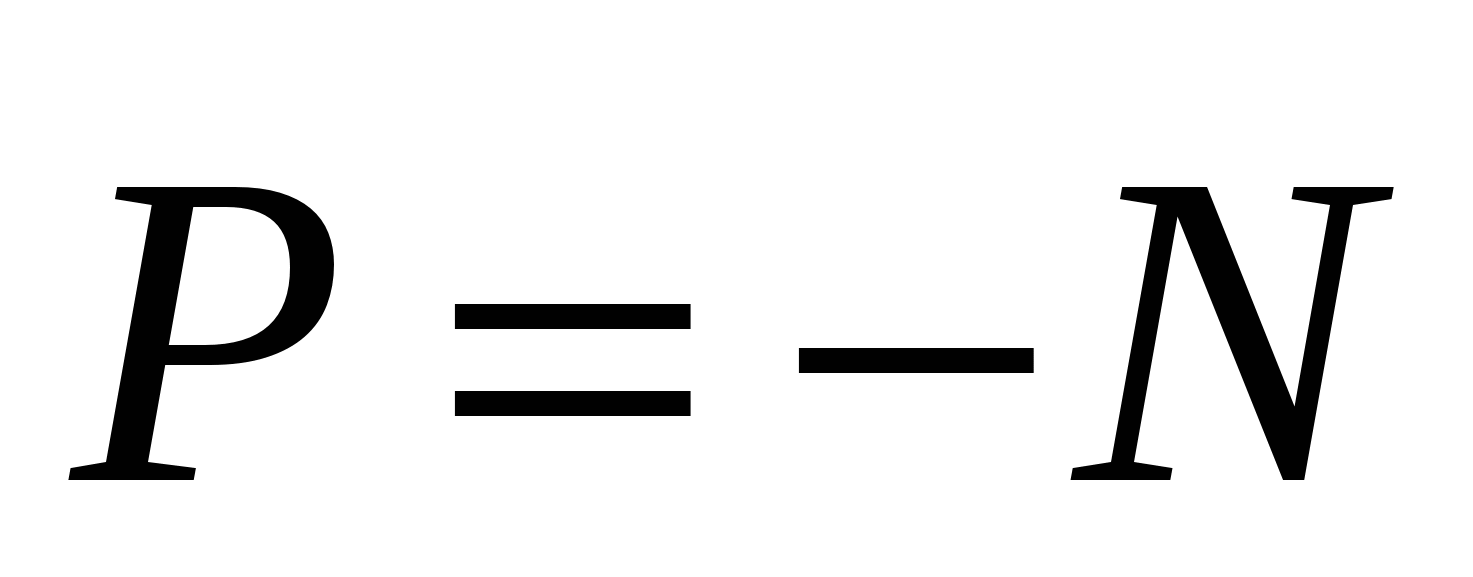 . Если тело неподвижно висит или лежит (или вместе с подставкой движется равномерно, – система отсчёта инерциальна), то по второму закону Ньютона, сумма сил, действующих на тело, то есть тяжести и нормального давления, будет равна нулю (ускорение отсутствует):
. Если тело неподвижно висит или лежит (или вместе с подставкой движется равномерно, – система отсчёта инерциальна), то по второму закону Ньютона, сумма сил, действующих на тело, то есть тяжести и нормального давления, будет равна нулю (ускорение отсутствует): 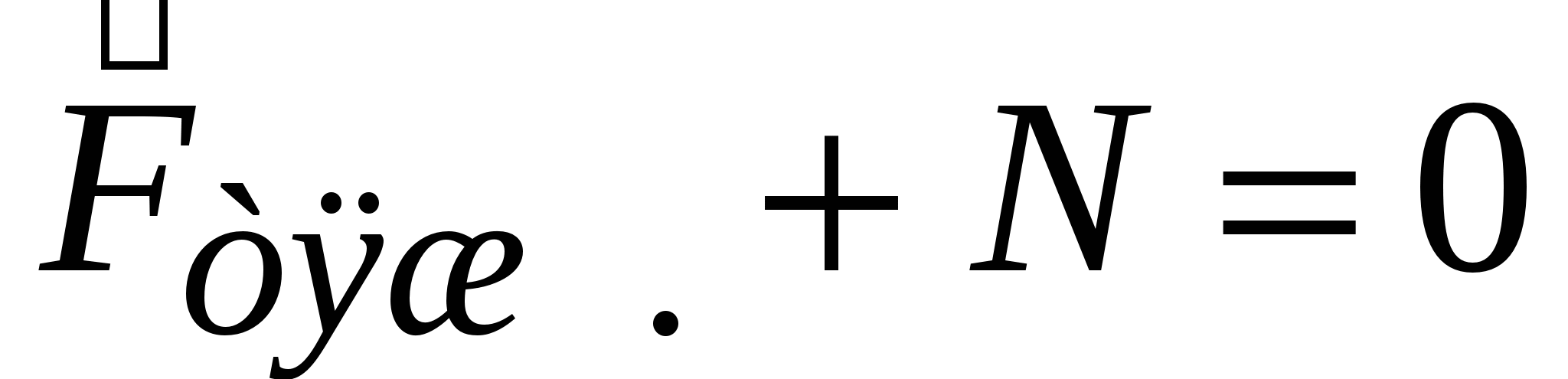 . Тогда вес
. Тогда вес 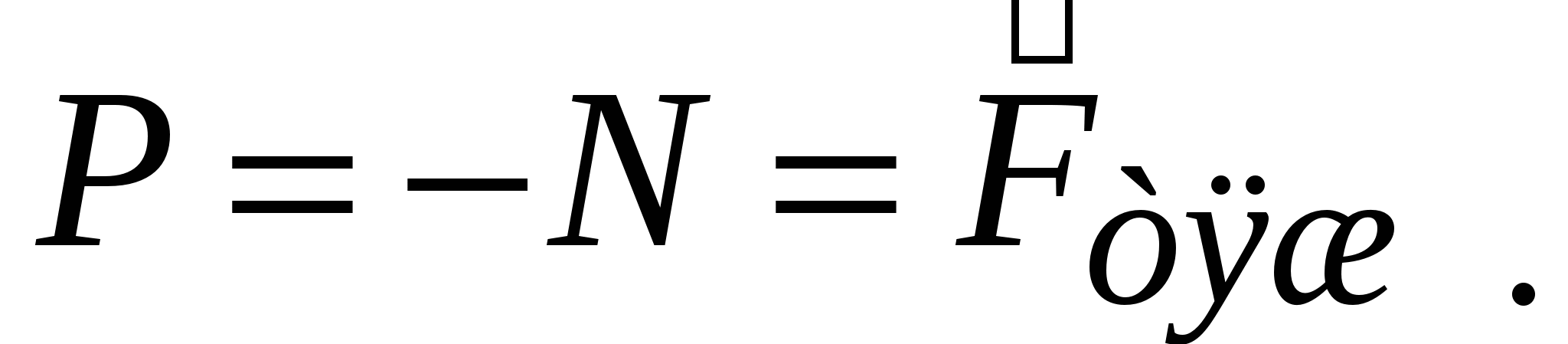 . Если тело движется ускоренно (
. Если тело движется ускоренно ( 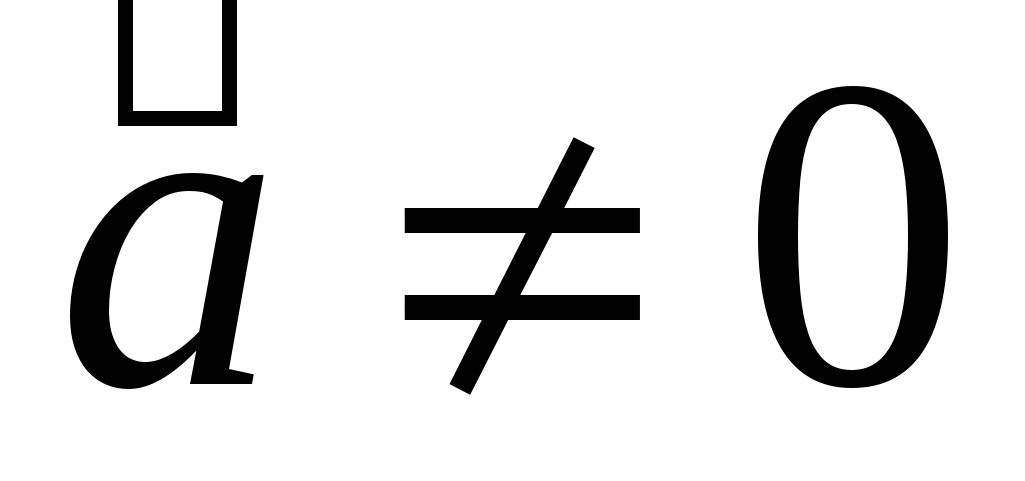 ) вместе с подставкой, то уравнение движения примет вид
) вместе с подставкой, то уравнение движения примет вид 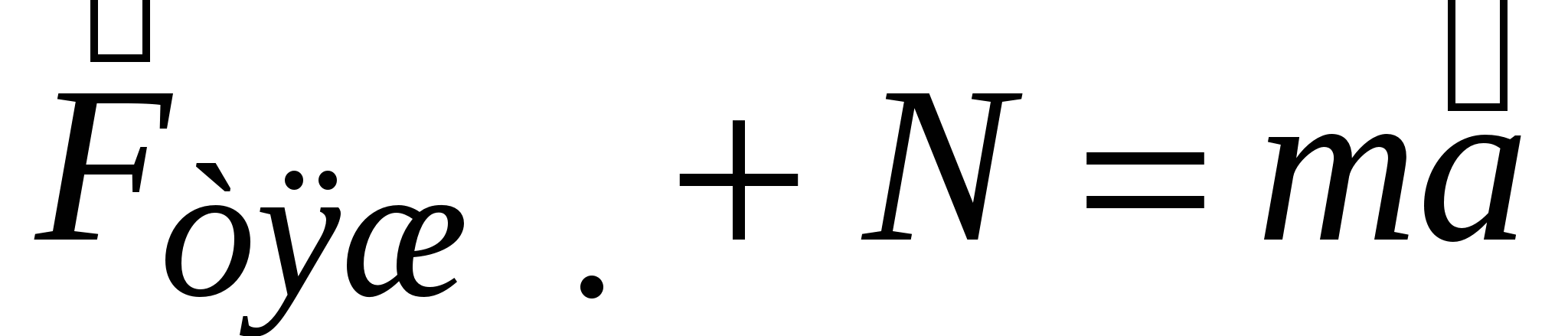 , и вес
, и вес 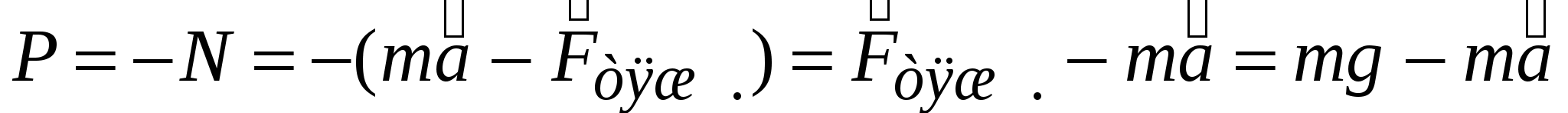 . Если, например, тело вместе с лифтом движется ускоренно вверх (рис.2.2), то в проекциях на ось OY
. Если, например, тело вместе с лифтом движется ускоренно вверх (рис.2.2), то в проекциях на ось OY 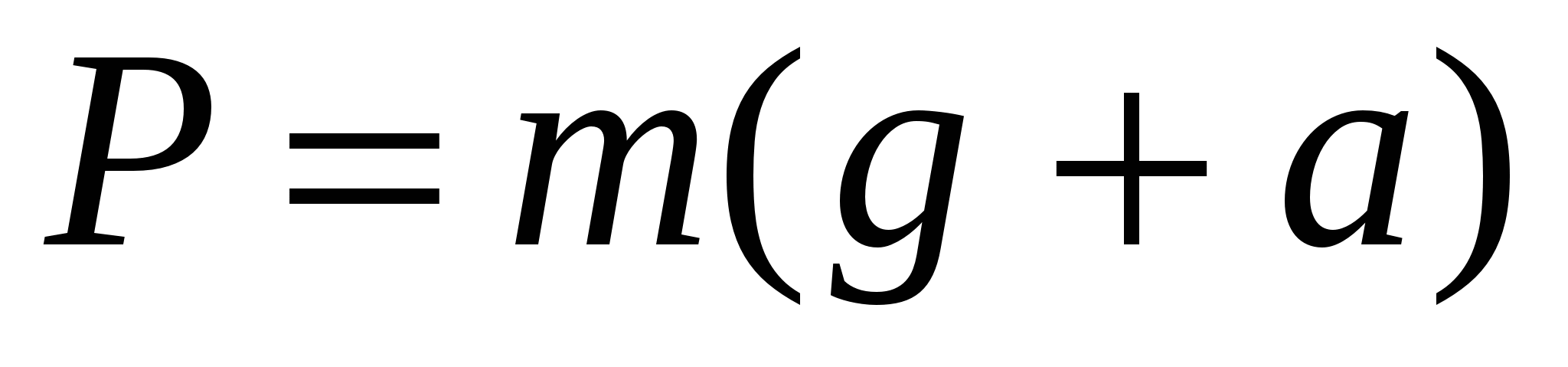 . (2.11) Если ускорение направлено вниз, то вес
. (2.11) Если ускорение направлено вниз, то вес 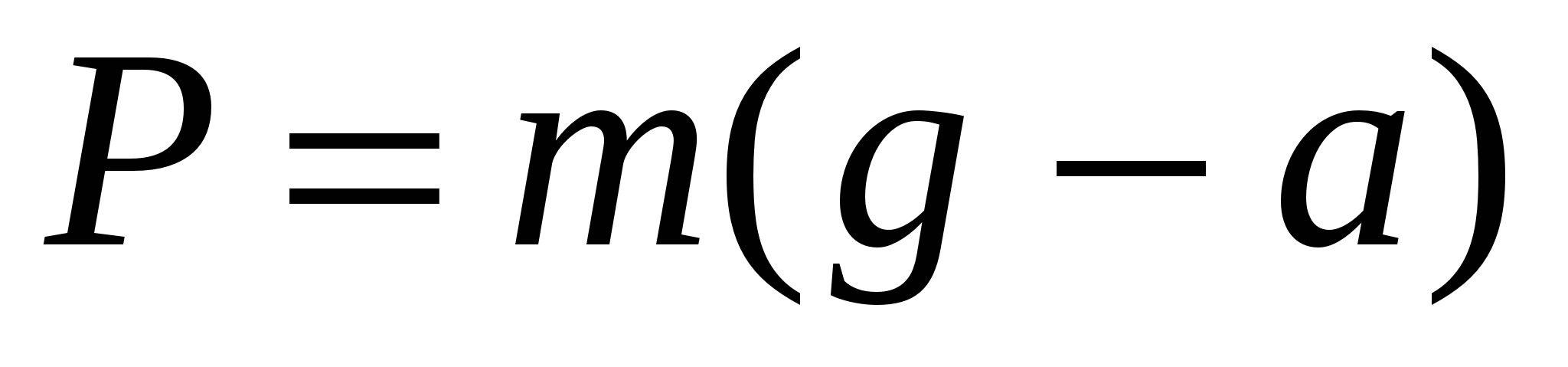 . (2.12) При
. (2.12) При 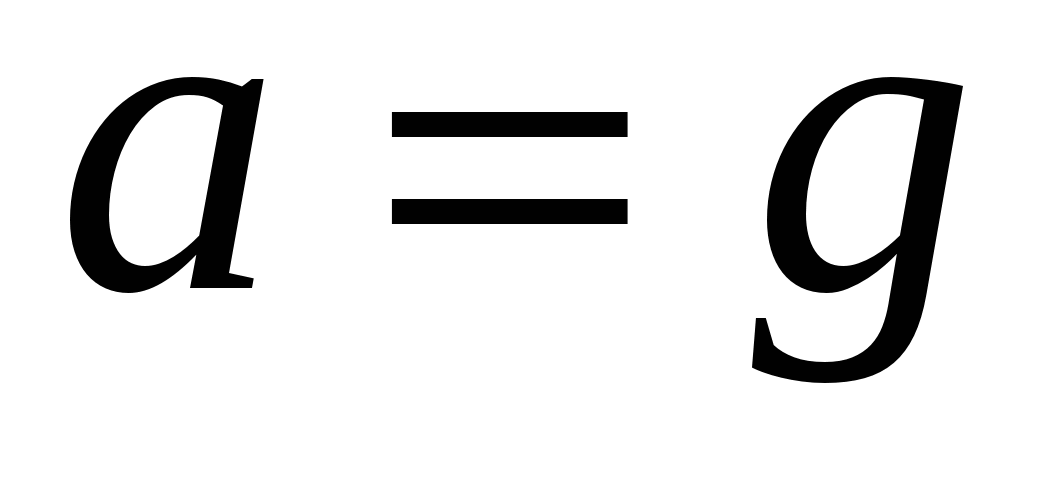 наступает невесомость:
наступает невесомость: 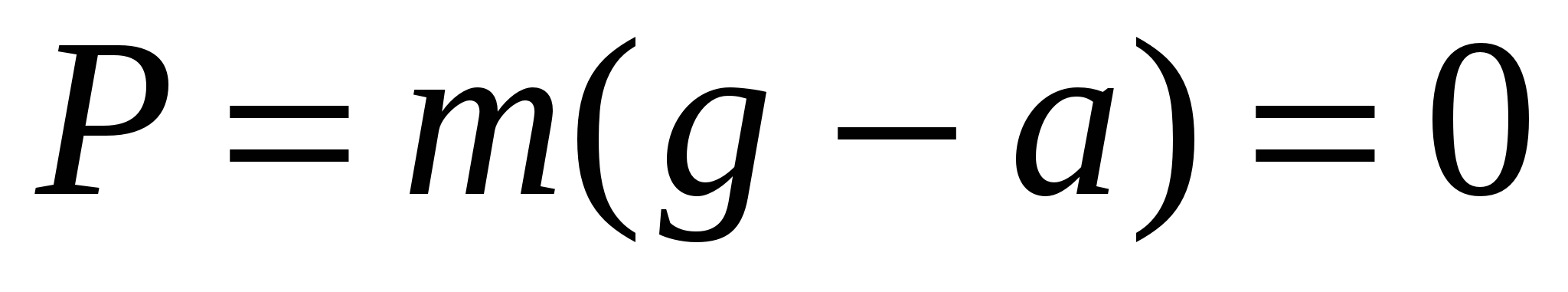 .
. 
Сила трения. Сила трения возникает при относительном перемещении соприкасающихся тел (или частей одного тела).
| Трение | |||||
| Сухое | Вязкое | ||||
| Покоя | Скольжения | Качения | |||
Будем рассматривать только сухое трение покоя и скольжения. Сила трения скольжения зависит от того, с какой силой прижаты тела друг к другу (от силы нормального давления  ):
): 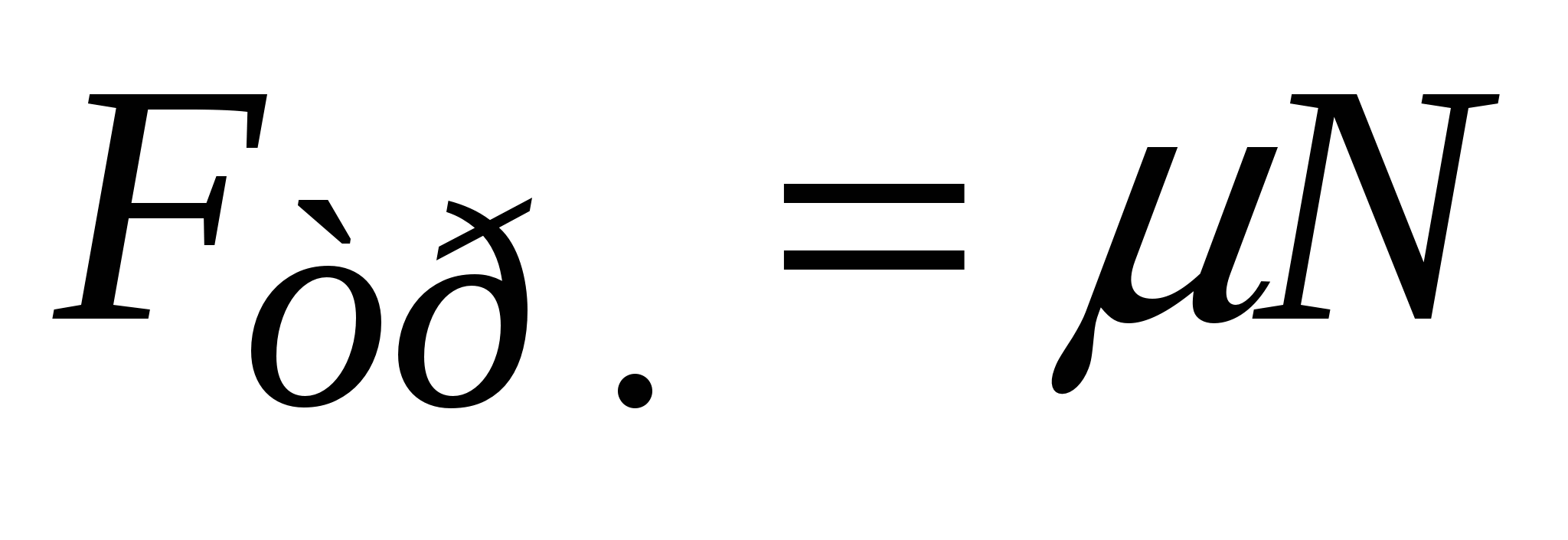 . (2.13) Здесь
. (2.13) Здесь  – коэффициент трения; он безразмерен; его величина не может быть больше единицы. Считаем, что в первом приближении сила трения скольжения не зависит от скорости. Сила трения покоя возникает при попытках переместить соприкасающиеся тела относительно друг друга (рис.2.3). Она может принимать любые значения от 0 до
– коэффициент трения; он безразмерен; его величина не может быть больше единицы. Считаем, что в первом приближении сила трения скольжения не зависит от скорости. Сила трения покоя возникает при попытках переместить соприкасающиеся тела относительно друг друга (рис.2.3). Она может принимать любые значения от 0 до  :
: 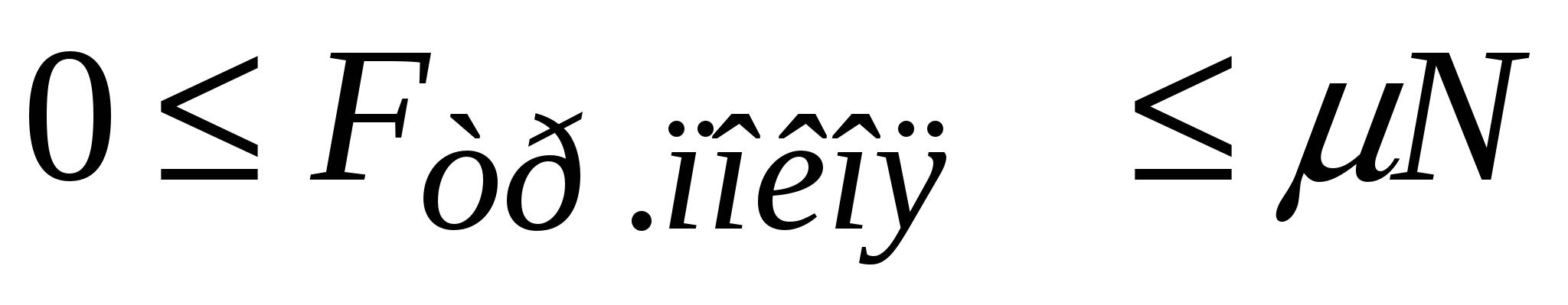 . Пока тело не сдвинулось, внешняя сила и сила трения покоя уравновешивают друг друга; с увеличением
. Пока тело не сдвинулось, внешняя сила и сила трения покоя уравновешивают друг друга; с увеличением  растёт и
растёт и 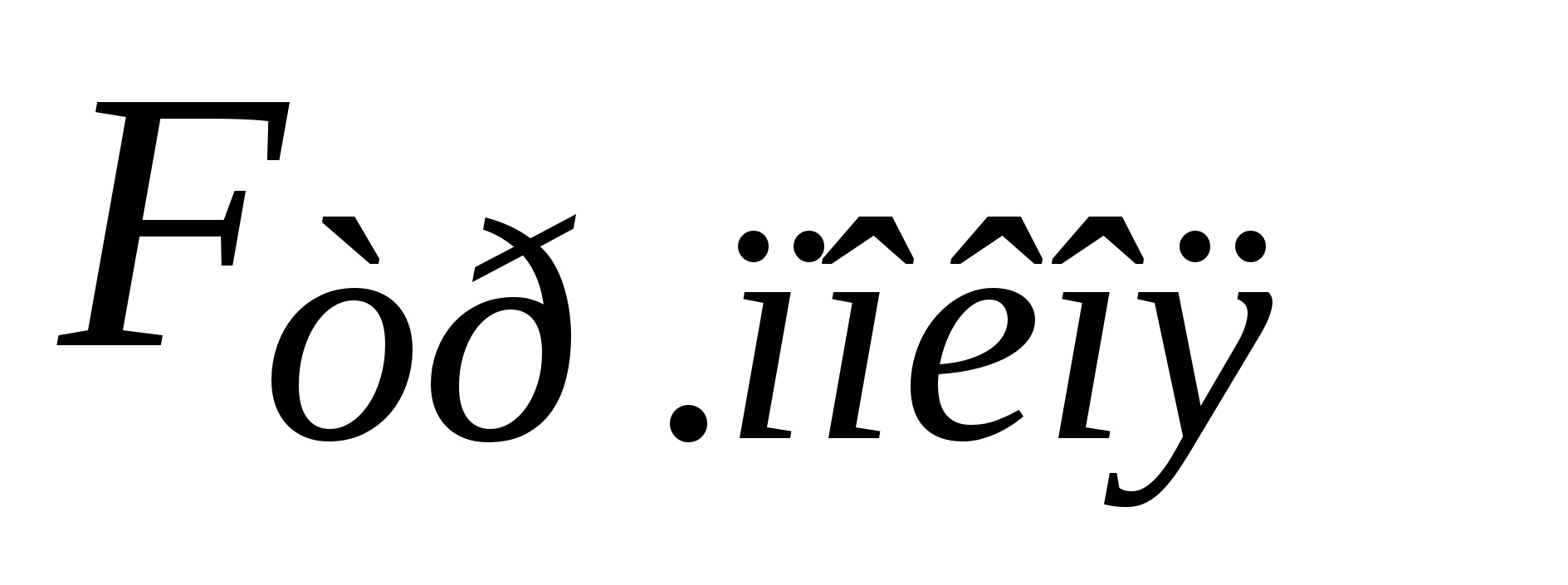 (участок 1 на рис.2.43):
(участок 1 на рис.2.43): 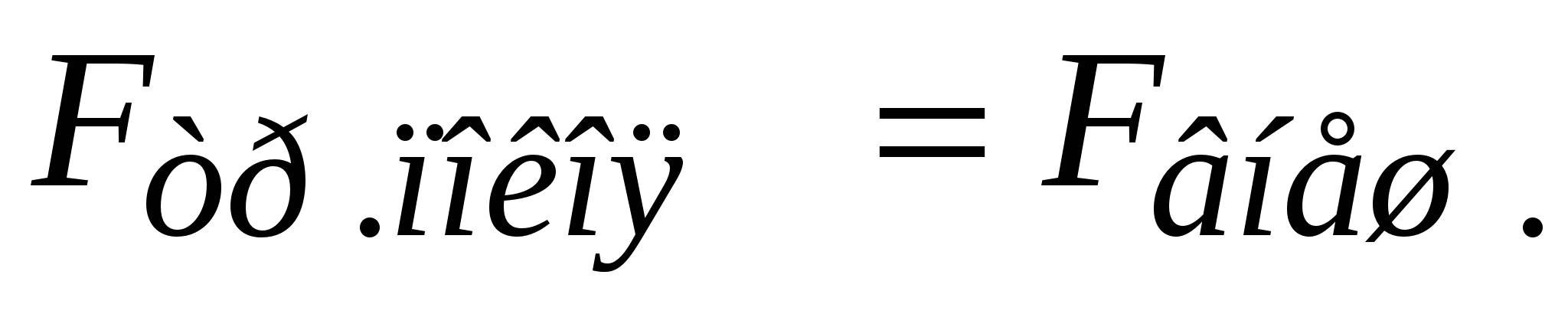 . Если внешняя сила превышает максимально возможное значение силы трения покоя, равное
. Если внешняя сила превышает максимально возможное значение силы трения покоя, равное  , то тело сдвинется, и сила трения покоя перейдёт в силу трения скольжения (участок 2 на рис.2.4). Сила трения направлена по касательной с соприкасающимся поверхностям (рис.2.3). Причины возникновения сил трения – неровности, шероховатости поверхностей тел: при относительном перемещении неровности зацепляются, ломаются; при этом тратится энергия – тела нагреваются. Ещё одна причина – межмолекулярное (межатомное) взаимодействие: при соприкосновении частицы двух тел притягиваются. В конечном итоге трение – проявление электромагнитного взаимодействия.
, то тело сдвинется, и сила трения покоя перейдёт в силу трения скольжения (участок 2 на рис.2.4). Сила трения направлена по касательной с соприкасающимся поверхностям (рис.2.3). Причины возникновения сил трения – неровности, шероховатости поверхностей тел: при относительном перемещении неровности зацепляются, ломаются; при этом тратится энергия – тела нагреваются. Ещё одна причина – межмолекулярное (межатомное) взаимодействие: при соприкосновении частицы двух тел притягиваются. В конечном итоге трение – проявление электромагнитного взаимодействия. 

Силы упругости Причины возникновения сил упругости – также межмолекулярные (межатомные) взаимодействия и сводятся к электромагнитным силам: при изменении длины тела (например, при растяжении) увеличиваются средние межатомные расстояния, в результате чего возникают силы притяжения между частицами, и тело стремится вернуться к первоначальным размерам. Деформация тела называется упругой, если после снятия нагрузки тело возвращается к первоначальным размерам и форме. Строго говоря, остаточная деформация есть всегда, но если она мала, ею пренебрегают. При неупругой деформации происходит разрыв некоторых межатомных связей и образование связей между другими атомами, в результате чего изменённая форма тела сохраняется и после снятия нагрузки. Любая деформация может быть представлена как сочетание двух основных: растяжения (сжатия) и сдвига (рис.2.5 и 2.6 соответственно). Рассмотрим деформацию растяжения стержня. При малых деформациях изменение длины тела, то есть абсолютная деформация 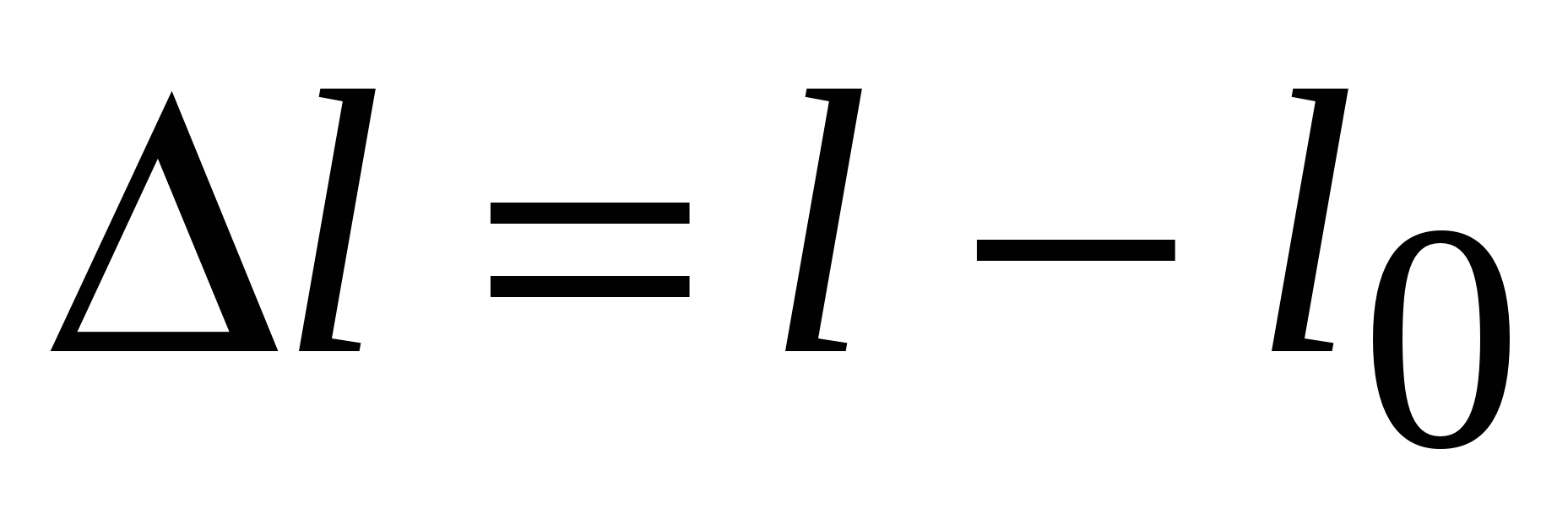 , прямо пропорциональна приложенной силе – это закон Гука:
, прямо пропорциональна приложенной силе – это закон Гука: 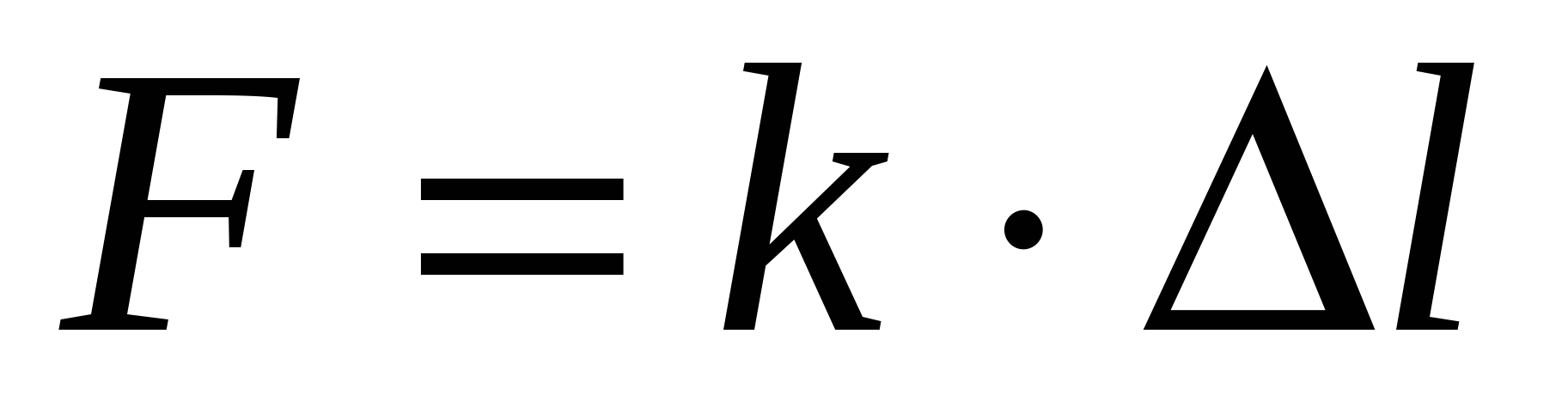 ; (2.14) здесь
; (2.14) здесь  – жёсткость. Закон Гука можно записать в локальной форме. Для этого введём новые величины: 1. Механическое нормальное напряжение σ – это сила, приходящаяся на единицу площади сечения тела (считаем силу приложенной перпендикулярно сечению
– жёсткость. Закон Гука можно записать в локальной форме. Для этого введём новые величины: 1. Механическое нормальное напряжение σ – это сила, приходящаяся на единицу площади сечения тела (считаем силу приложенной перпендикулярно сечению  ):
): 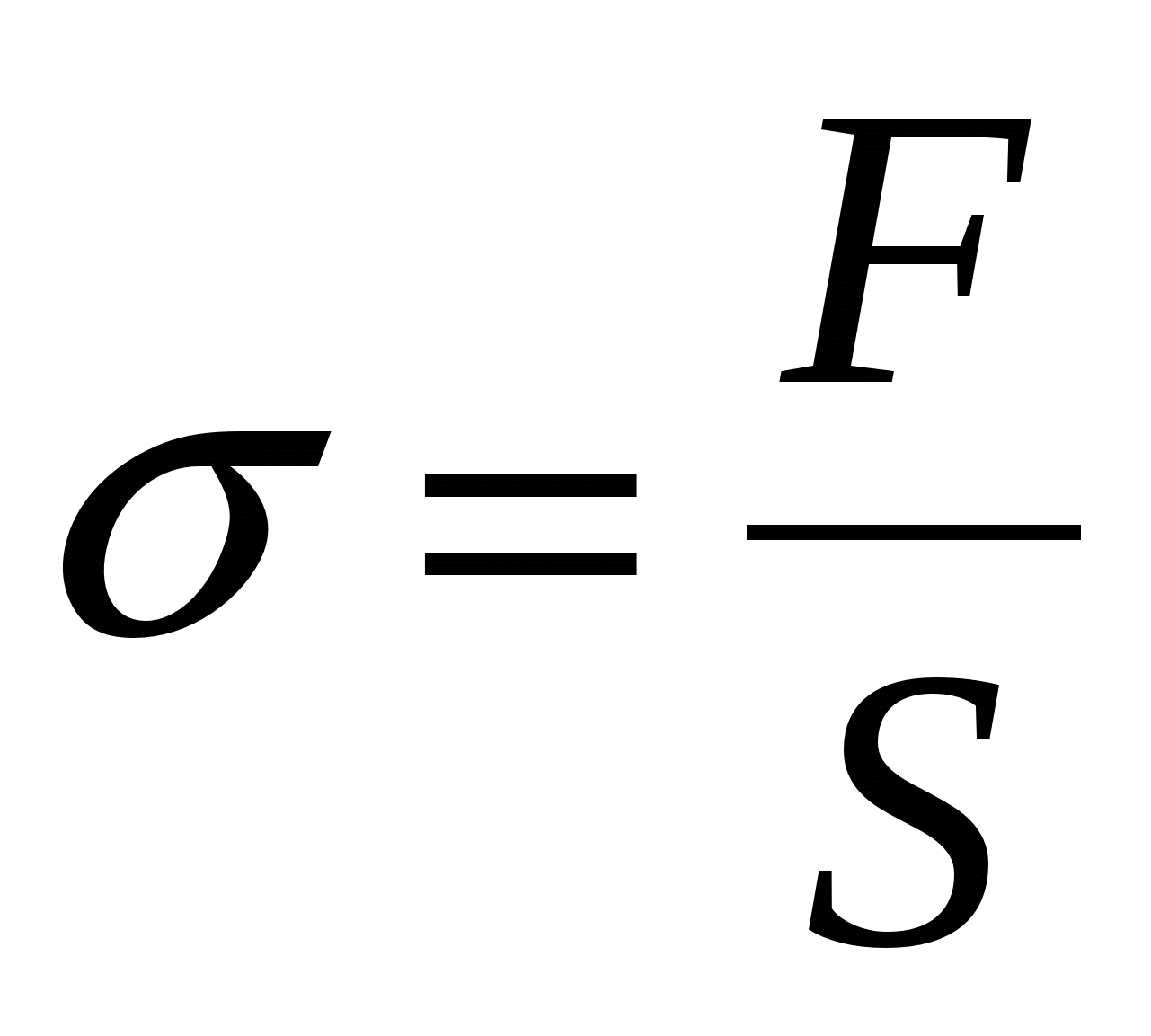 . (2.15) Механическое напряжение – локальная характеристика; в разных точках сечения оно, вообще говоря, может быть различным, поэтому лучше использовать определение (2.15а):
. (2.15) Механическое напряжение – локальная характеристика; в разных точках сечения оно, вообще говоря, может быть различным, поэтому лучше использовать определение (2.15а): 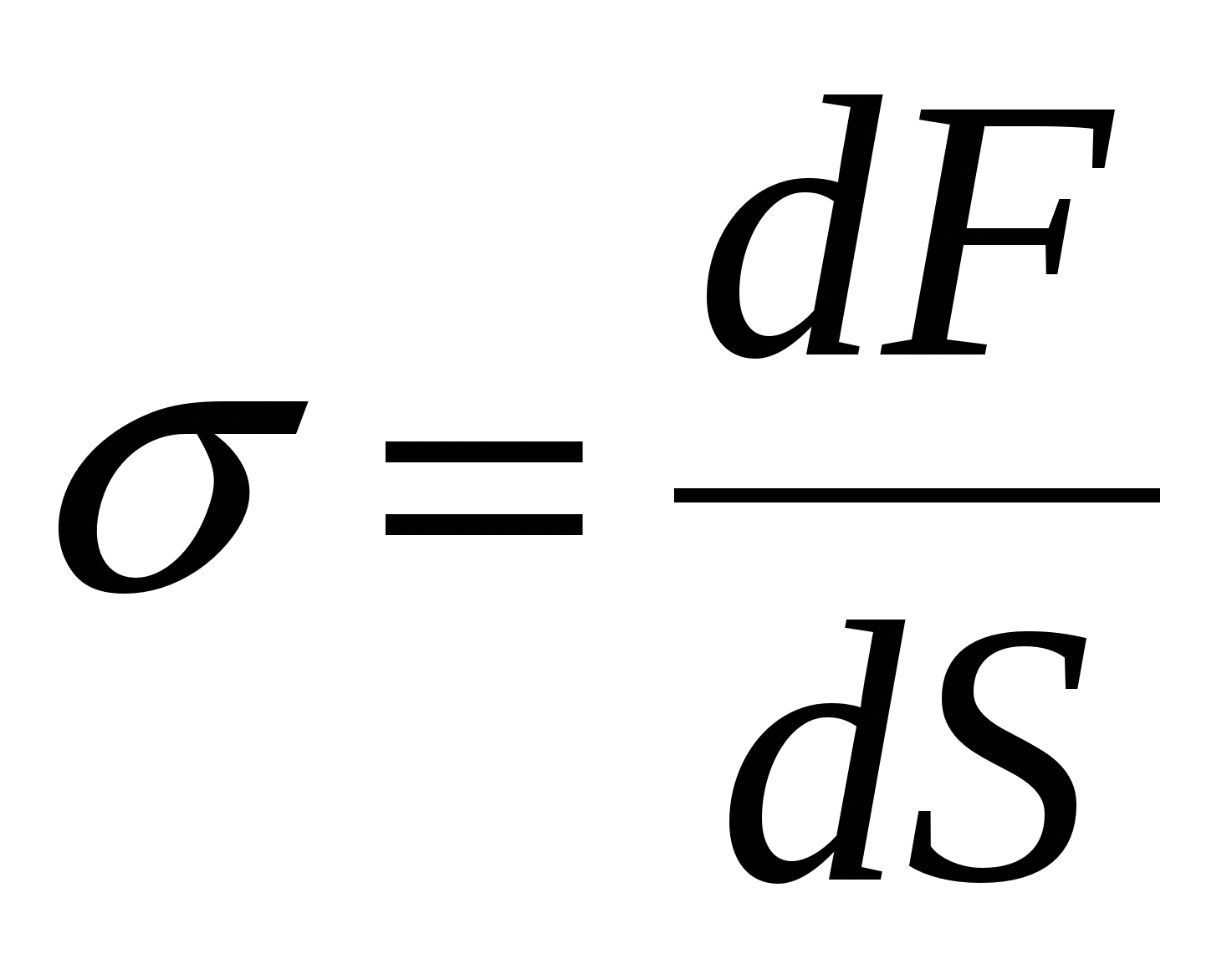 . (2.15а) Размерность
. (2.15а) Размерность 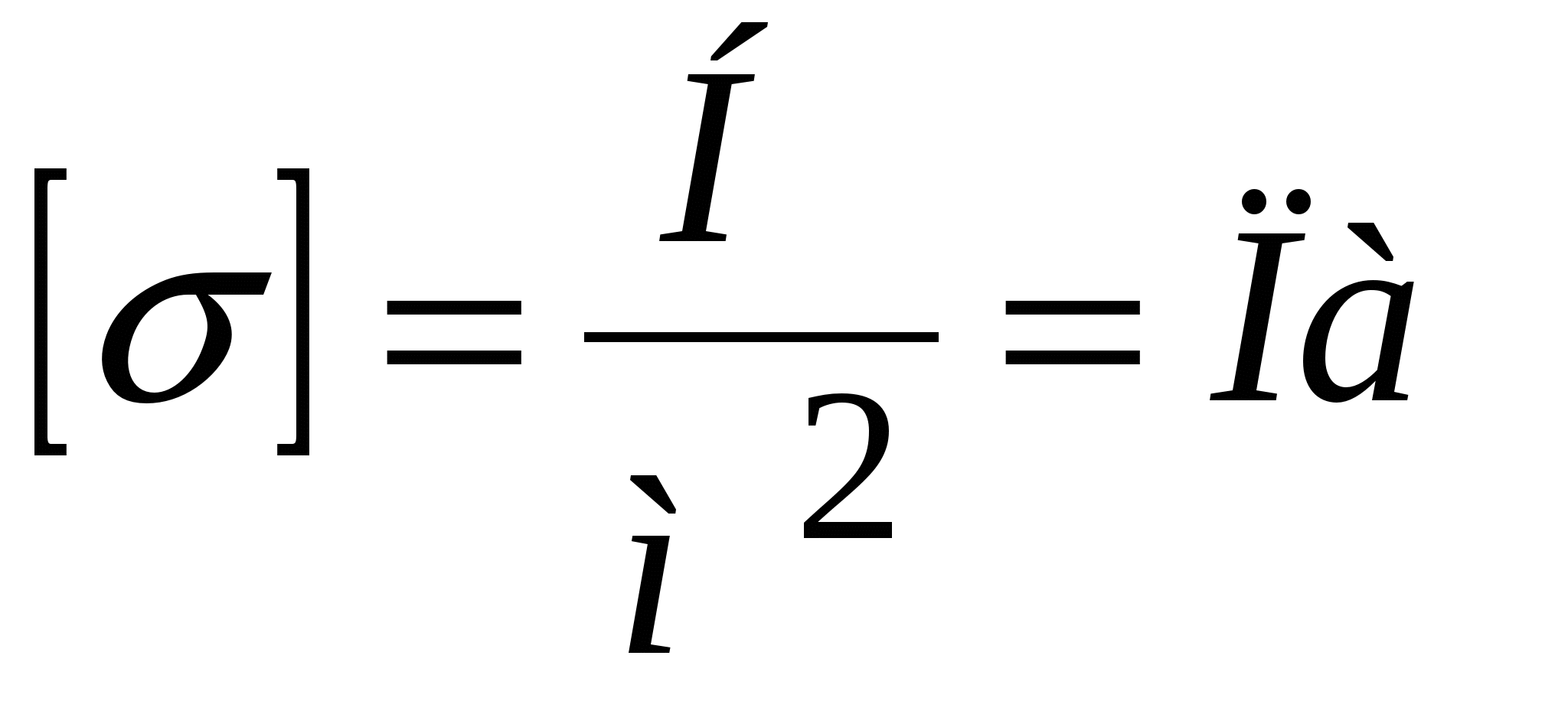 . 2. Относительная продольная деформация
. 2. Относительная продольная деформация  (или просто
(или просто 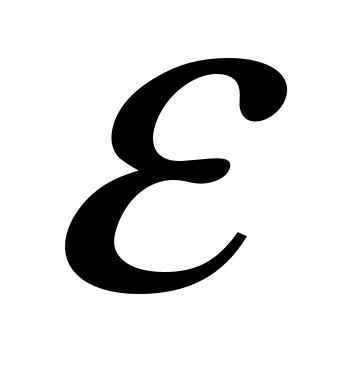 ) – это изменение длины по отношению к первоначальной длине:
) – это изменение длины по отношению к первоначальной длине: 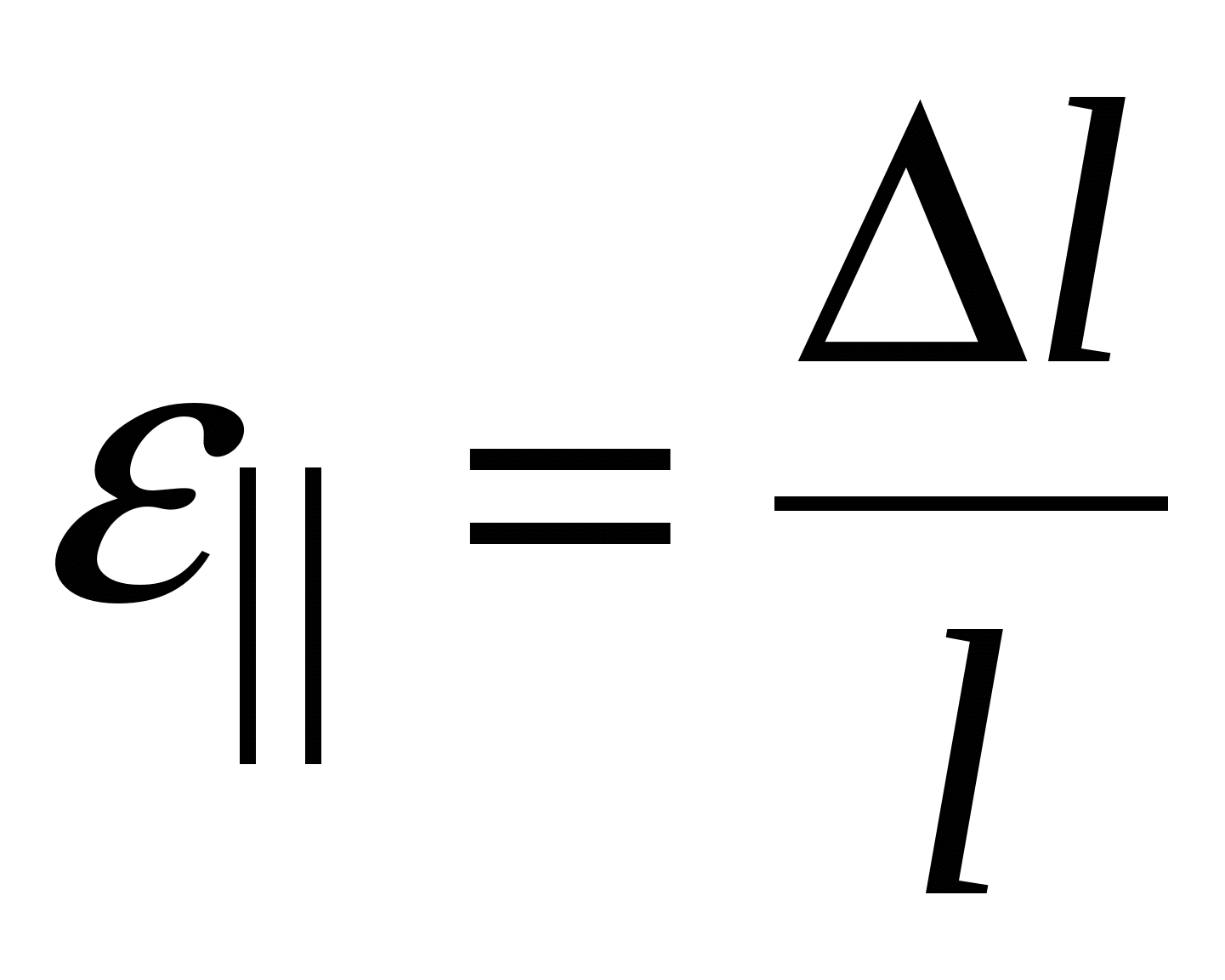 . (2.16) Она безразмерна:
. (2.16) Она безразмерна: 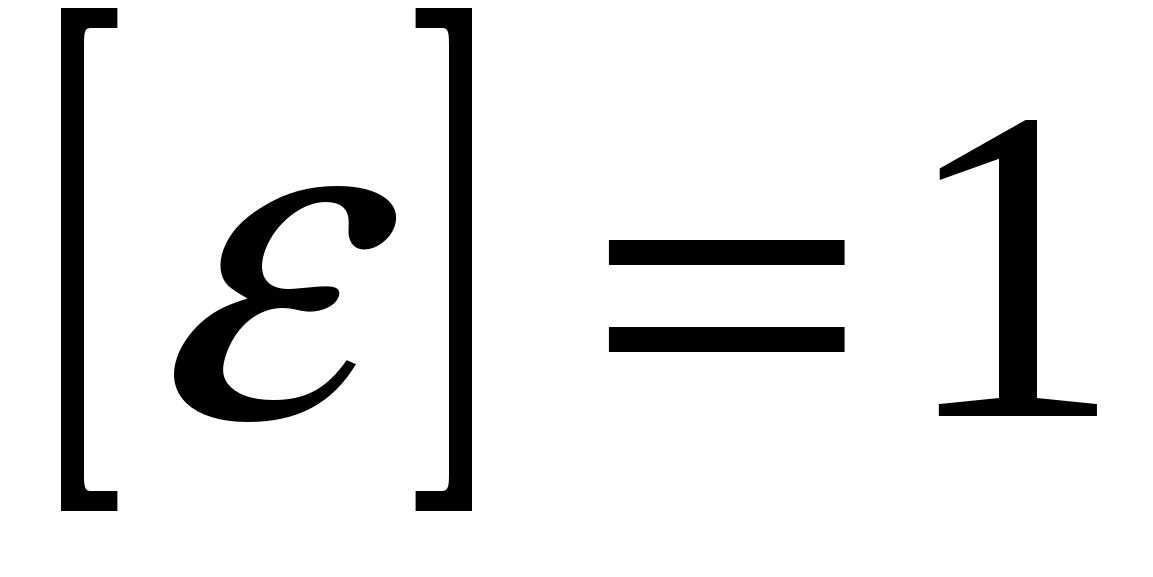 . Тогда закон Гука в локальной форме читается так: механическое напряжение прямо пропорционально относительной деформации:
. Тогда закон Гука в локальной форме читается так: механическое напряжение прямо пропорционально относительной деформации: 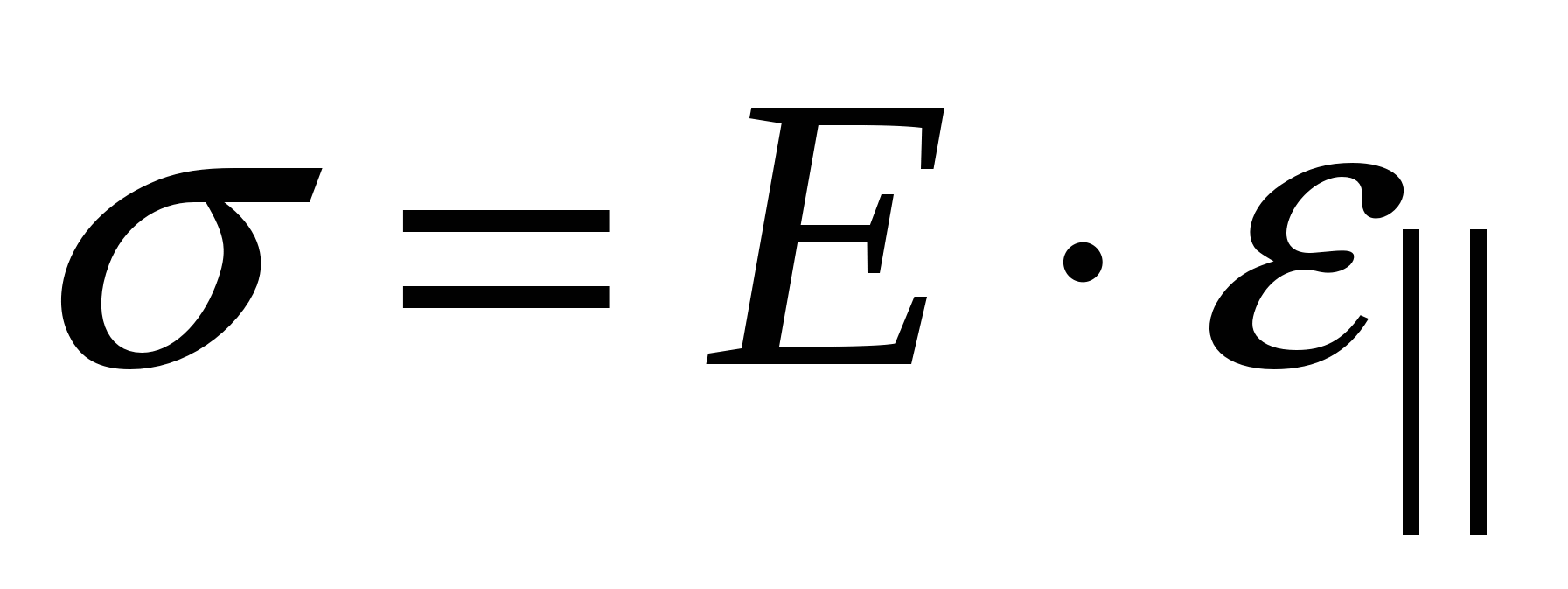 (2.17) Величина
(2.17) Величина  – это модуль Юнга материала и характеризует упругие свойства этого материала; не зависит от размеров и формы образца, в отличие от жёсткости
– это модуль Юнга материала и характеризует упругие свойства этого материала; не зависит от размеров и формы образца, в отличие от жёсткости  (2.18), и поэтому формулировка (2.17) более удобна и универсальна, чем (2.14). Можно найти соотношение между жёсткостью и модулем Юнга:
(2.18), и поэтому формулировка (2.17) более удобна и универсальна, чем (2.14). Можно найти соотношение между жёсткостью и модулем Юнга: 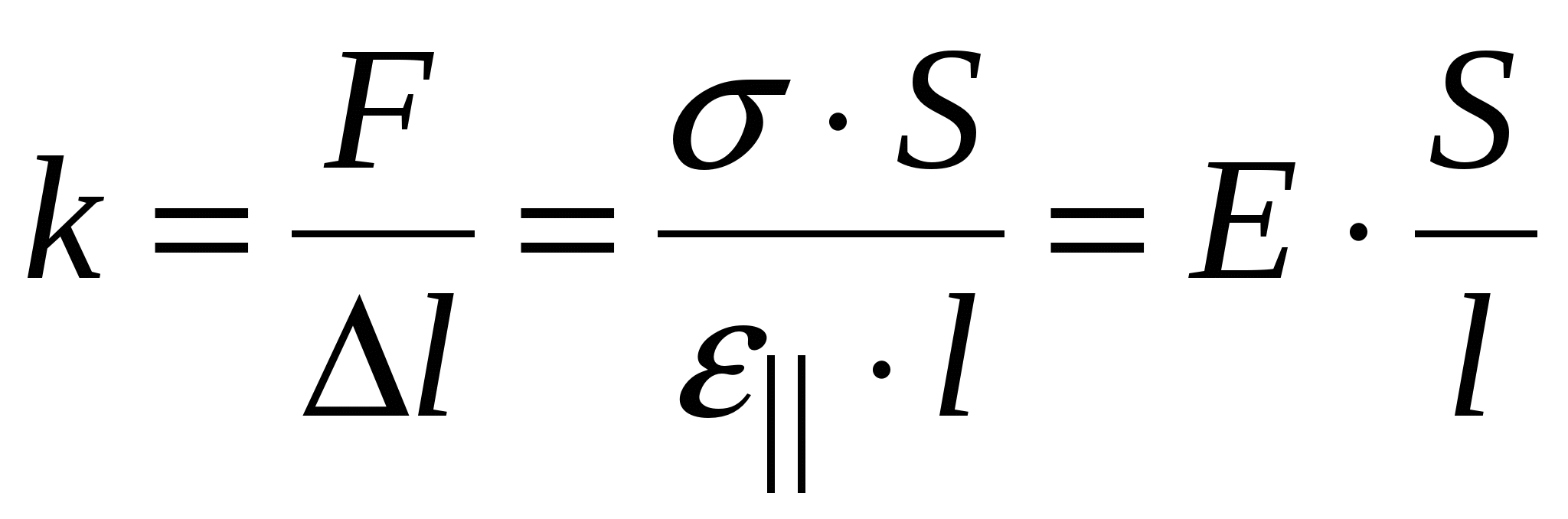 . (2.18) Размерность модуля Юнга:
. (2.18) Размерность модуля Юнга: 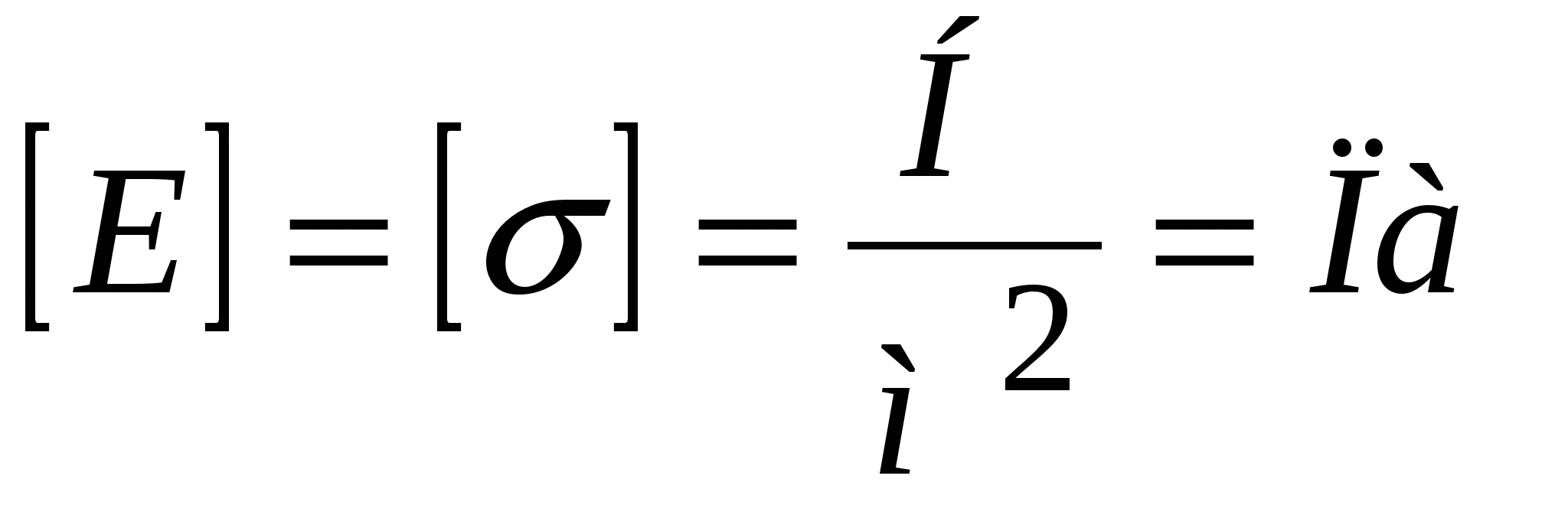 . Экспериментальная зависимость механического напряжения от относительной продольной деформации дана на рис.2.7. Там же указаны характерные точки – пределы: пропорциональности
. Экспериментальная зависимость механического напряжения от относительной продольной деформации дана на рис.2.7. Там же указаны характерные точки – пределы: пропорциональности 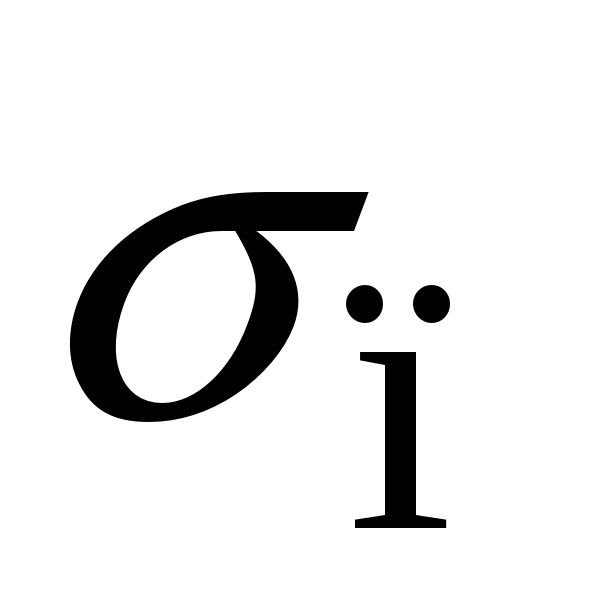 , упругости
, упругости 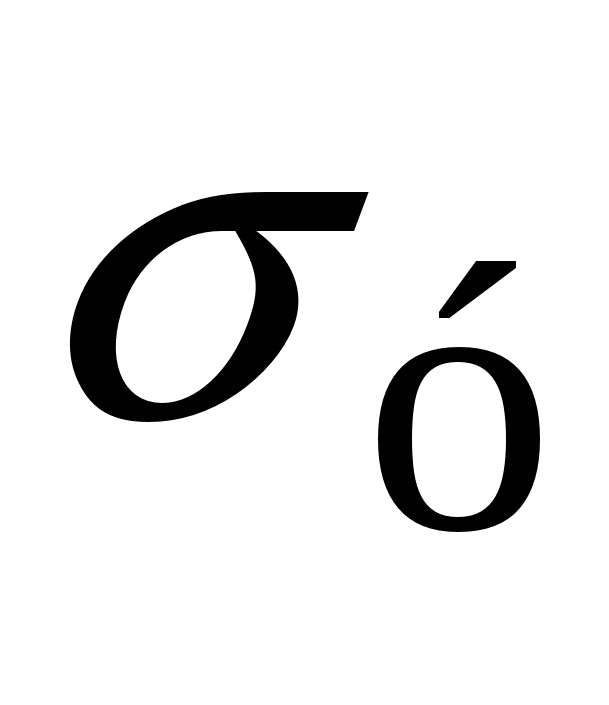 , текучести
, текучести 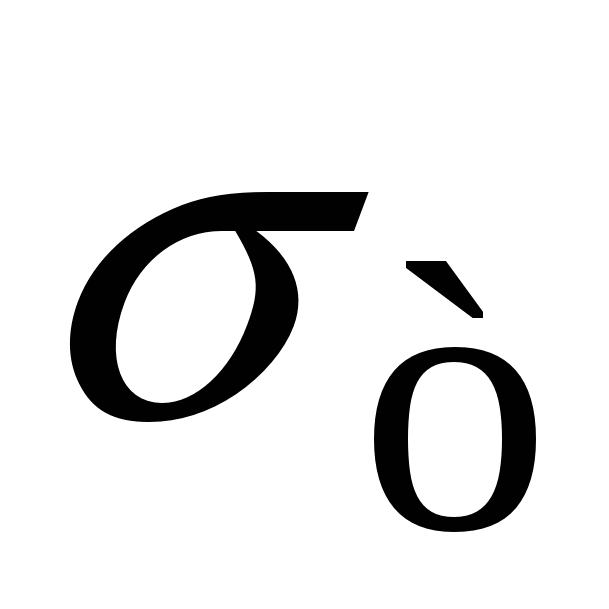 и прочности
и прочности 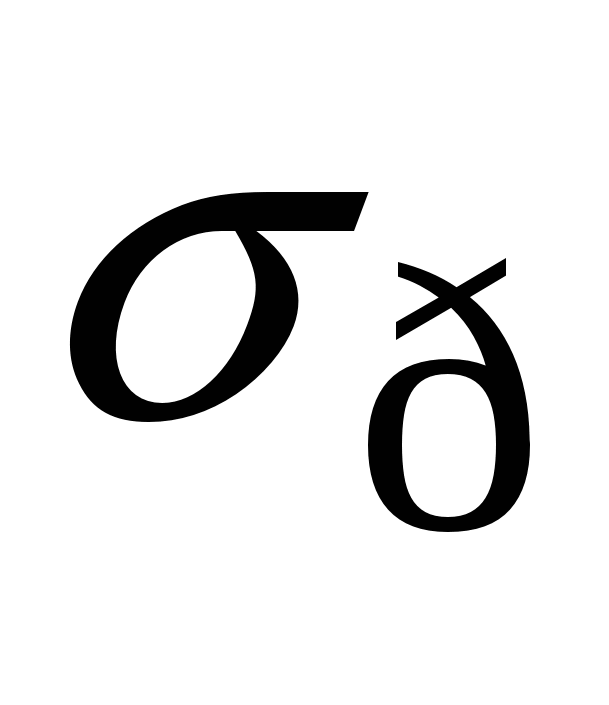 . Предел пропорциональности
. Предел пропорциональности 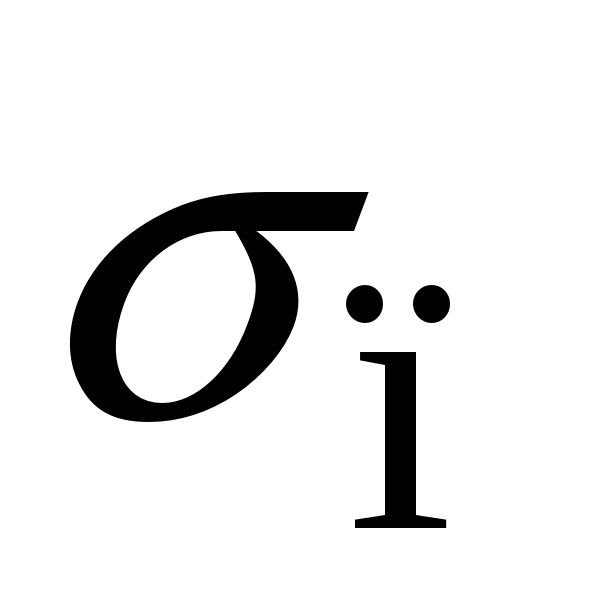 – это максимальное механическое напряжение, при котором ещё выполняется закон Гука (деформацию можно считать пропорциональной напряжению). Предел упругости
– это максимальное механическое напряжение, при котором ещё выполняется закон Гука (деформацию можно считать пропорциональной напряжению). Предел упругости 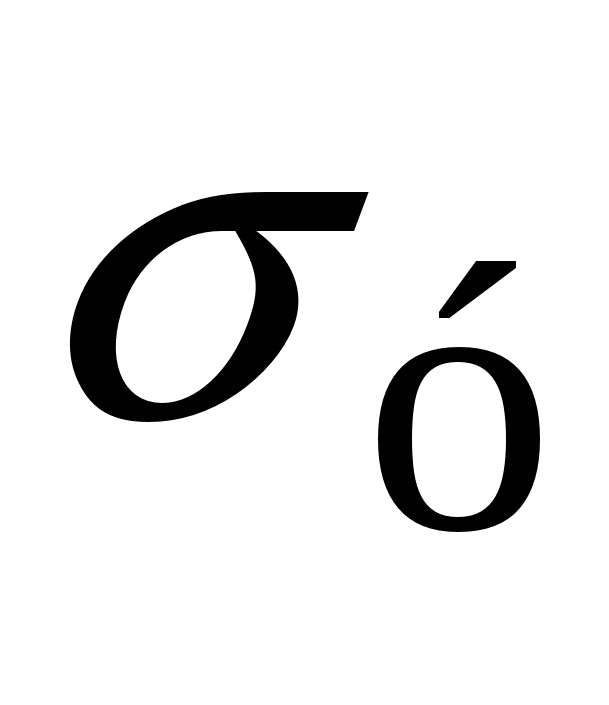 – такое максимальное напряжение, при котором деформацию можно считать упругой. Если напряжение превысит этот предел, после снятия нагрузки будет остаточная деформация. Предел текучести
– такое максимальное напряжение, при котором деформацию можно считать упругой. Если напряжение превысит этот предел, после снятия нагрузки будет остаточная деформация. Предел текучести 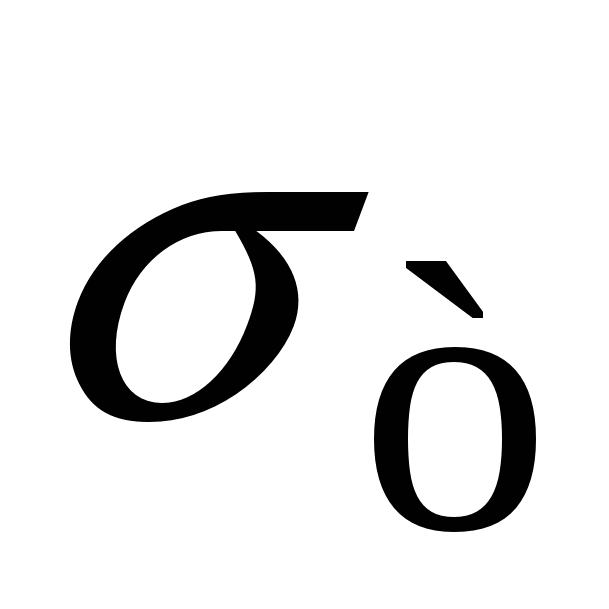 – это механическое напряжение, при котором деформация увеличивается почти без увеличения нагрузки. Горизонталь на графике – это область пластичности. Если тело пластично, этот участок длинный (сталь), если горизонтальный участок мал – тело хрупкое (чугун). Предел прочности
– это механическое напряжение, при котором деформация увеличивается почти без увеличения нагрузки. Горизонталь на графике – это область пластичности. Если тело пластично, этот участок длинный (сталь), если горизонтальный участок мал – тело хрупкое (чугун). Предел прочности 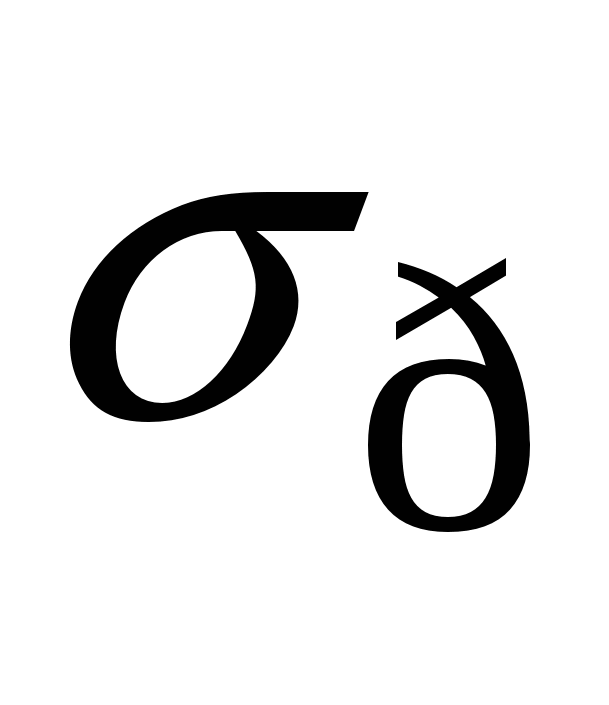 – это напряжение, при котором начинается разрушение тела. При деформации (удлинении) тела изменяется (уменьшается) сечение, и вообще говоря, изменяется объём. Относительное поперечное сжатие – это
– это напряжение, при котором начинается разрушение тела. При деформации (удлинении) тела изменяется (уменьшается) сечение, и вообще говоря, изменяется объём. Относительное поперечное сжатие – это 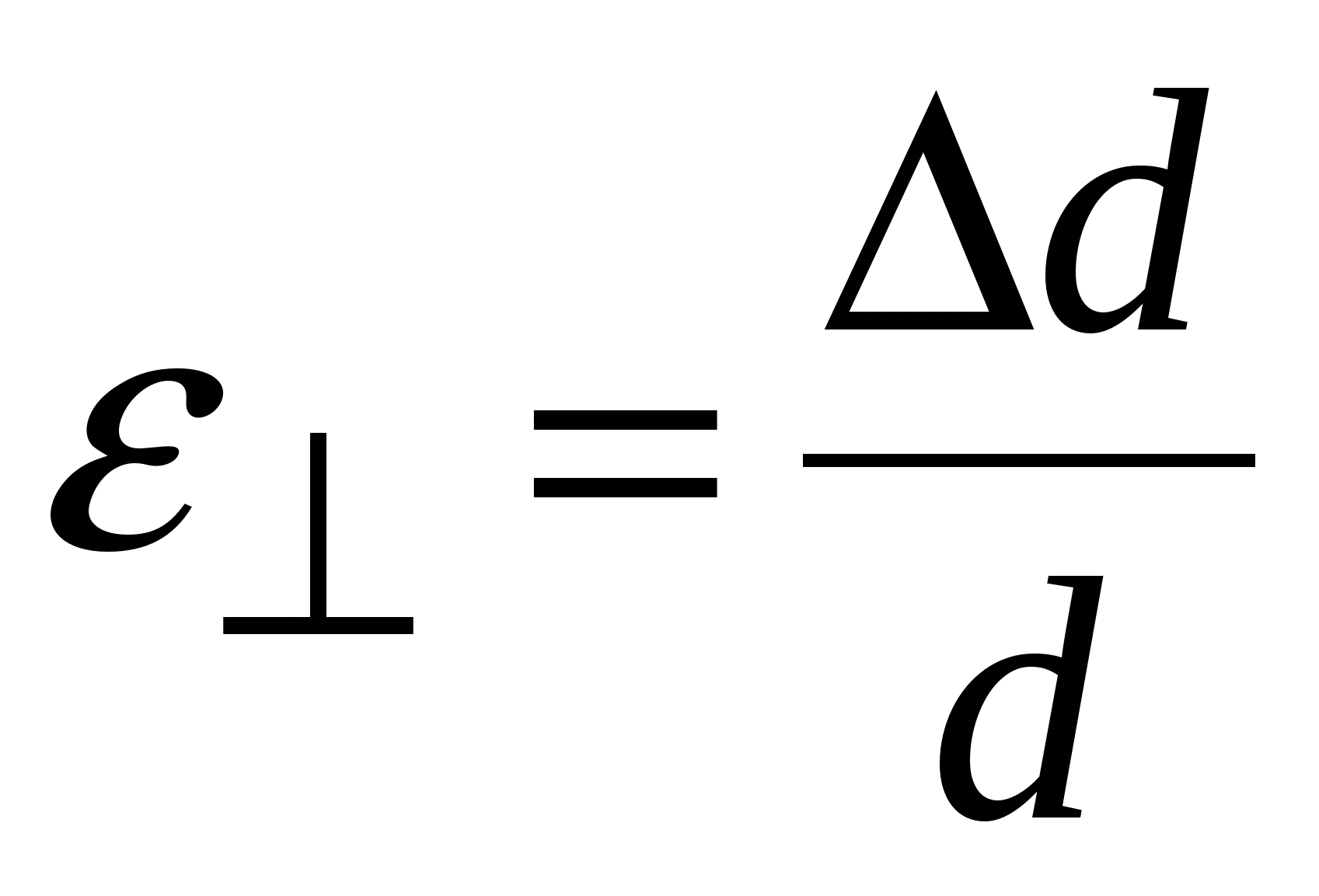 . (2.19) При односторонней деформации величины
. (2.19) При односторонней деформации величины 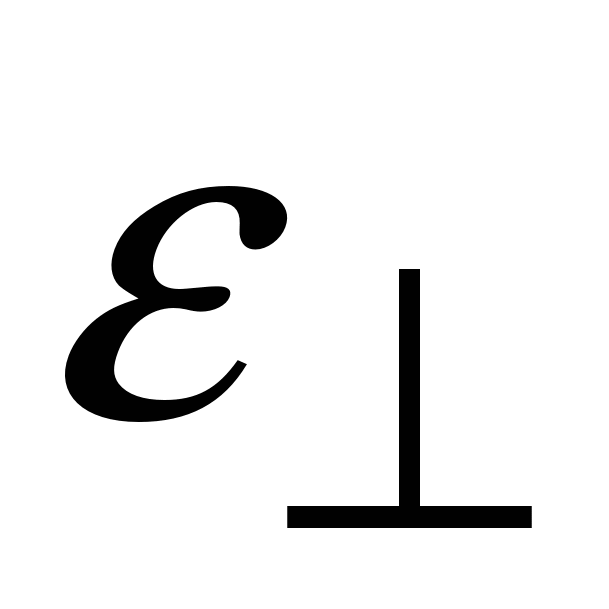 и
и  имеют противоположные знаки: при растяжении сечение уменьшается. Отношение этих величин – коэффициент Пуассона материала:
имеют противоположные знаки: при растяжении сечение уменьшается. Отношение этих величин – коэффициент Пуассона материала: 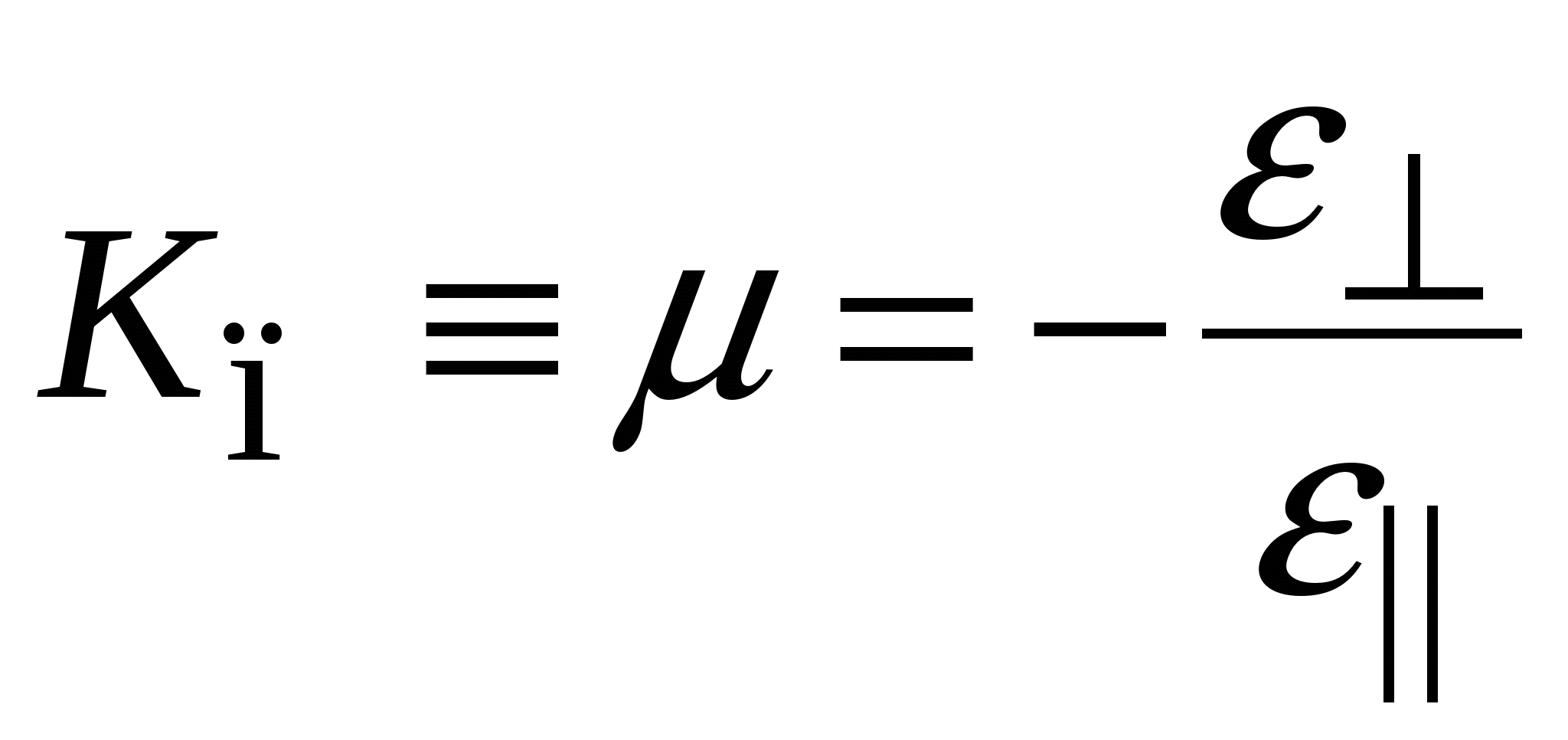 . (2.20) Можно доказать, что коэффициент Пуассона материалов, сохраняющих объём при деформациях, равен
. (2.20) Можно доказать, что коэффициент Пуассона материалов, сохраняющих объём при деформациях, равен 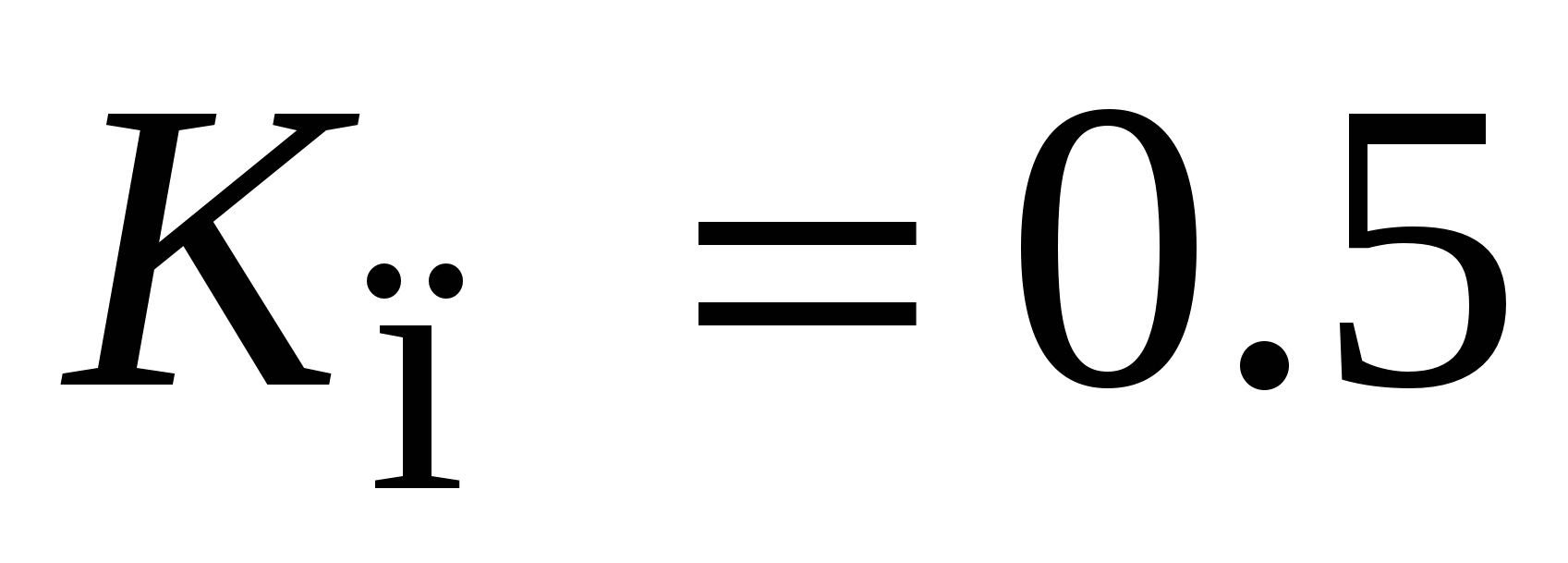 .
. 

4. Момент инерции материальной точки относительно оси вращения - произведение массы этой точки на квадрат расстояния от оси.
При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела, так и от положения и направления оси вращения.
Момент инерции твердого тела - это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.
Формула момента инерции:
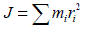
Единица момента инерции - килограмм-метр в квадрате.
Теорема Штейнера:
Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R - расстояние между осями.
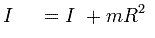

Угловое ускорение, которое тело приобретает под действием момента сил, прямо пропорционально результирующему моменту всех внешних сил, приложенных к телу, и обратно пропорциональна моменту инерции тела относительно некоторой оси.
Молекулярная физика
Вещество может находиться в трех агрегатных состояниях: твердом, жидком и газообразном. Молекулярная физика - раздел физики, в котором изучаются физические свойства тел в различных агрегатных состояниях на основе их молекулярного строения.
Тепловое движение - беспорядочное (хаотическое) движение атомов или молекул вещества.
ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
Молекулярно-кинетическая теория - теория, объясняющая тепловые явления в макроскопических телах и свойства этих тел на основе их молекулярного строения.
Основные положения молекулярно-кинетической теории:
вещество состоит из частиц - молекул и атомов, разделенных промежутками,
эти частицы хаотически движутся,
частицы взаимодействуют друг с другом.
МАССА И РАЗМЕРЫ МОЛЕКУЛ
Массы молекул и атомов очень малы. Например, масса одной молекулы водорода равна примерно 3,34*10 -27 кг, кислорода - 5,32*10 -26 кг. Масса одного атома углерода m0C=1,995*10 -26 кг
Относительной молекулярной (или атомной) массой вещества Mr называют отношение массы молекулы (или атома) данного вещества к 1/12 массы атома углерода:(атомная единица массы).
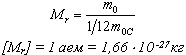
Количество вещества - это отношение числа молекул N в данном теле к числу атомов в 0,012 кг углерода NA:
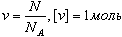
Моль - количество вещества, содержащего столько молекул, сколько содержится атомов в 0,012 кг углерода.
Число молекул или атомов в 1 моле вещества называют постоянной Авогадро:
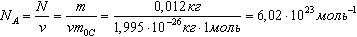
Молярная масса - масса 1 моля вещества:
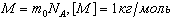
Молярная и относительная молекулярная массы вещества связаны соотношением: М = Мr*10 -3 кг/моль.
СКОРОСТЬ ДВИЖЕНИЯ МОЛЕКУЛ
Несмотря на беспорядочный характер движения молекул, их распределение по скоростям носит характер определенной закономерности, которая называется распределением Максвелла.

График, характеризующий это распределение, называют кривой распределения Максвелла. Она показывает, что в системе молекул при данной температуре есть очень быстрые и очень медленные, но большая часть молекул движется с определенной скоростью, которая называется наиболее вероятной. При повышении температуры эта наиболее вероятная скорость увеличивается.
Дата: 2018-12-28, просмотров: 1131.