· 1. Объединением множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
· 2. Пересечением множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Декартово произведение двух множеств — это множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств.
Граф – это математический объект, который является совокупностью 2-ух множеств.
Множества точек и множества линий.
Точки – это вершины графа.
Линии – рёбра графа.
Вершины графа – это элемент графа, обозначающий объект любой природы, входящий в множество объектов, описываемое графом.
Изолированная вершина — вершина, не соединённая с другими вершинами ни дугами, ни рёбрами. однако такая вершина может иметь петли.
Степень вершины графа — количество рёбер графа инцидентных вершине.
Смежные вершины - вершины, соединённые ребром.
Ориентированный граф – это граф, рёбрам которого присвоено направление.
Граф без дуг (то есть неориентированный), без петель и кратных рёбер называется обыкновенным.
Взвешенным графом называется граф, вершинам и (или) рёбрам которого присвоены некоторые числа.
Петля – это ребро, соединяющее вершину саму с собой.
Кратные - это два и более ребра, инцидентных одним и тем же двум вершинам.
18. Способ задания графов:графический, аналитический и матричный.
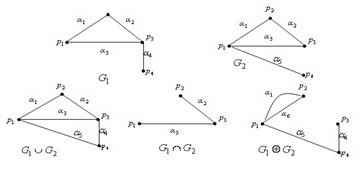
19. Объединением графов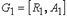 
и 
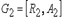называется граф 
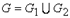, множество вершин которого есть объединение множеств вершин графов 
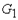и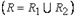 
, а множество ребер является объединением множеств ребер этих графов 
.
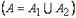Пересечением графов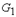 
и 
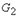называется граф 
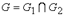, множество вершин которого 
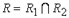, а множество ребер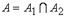 
. 
20. Булева функции: функция, которая отображает множество кортежей состоящих из 0 и 1 в множество (0;1).
Функции одной переменной: Функции одной переменной – функции, зависящие только от одного аргумента.
· Тождественной нулем - называется функция, которая принимает значение нуля при любых значениях аргументов. Функция обозначается «0».
· Тождественной функцией - называется функция, которая принимает значения равные значению аргумента. Функция обозначается «х».
· Инверсия - функция принимающая значения противоположные значениям аргумента. Обозначается «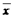 
».
· Тождественной единицей - называется, функция которая принимает значение единицы при любых значениях аргументов. Функция обозначается «1».
22. Область определения булевой функции: множество кортежей занятой длины.
Дата: 2018-12-28, просмотров: 236.
