Ответы к математической логике
Понятие множества
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком.
Конечность множества
Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным.
Мощность множества
Мощностью множества А называется количество входящих в его состав различных элементов и обозначается через !А! которое имеет смысл для всех множеств, включая бесконечные.
Универсальное множество — в математике множество, содержащее все объекты, все множества и понятия.
5. Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø.
Способы записи множеств: Словесный, Перечисление, Графический.
· 1. Объединением множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
· 2. Пересечением множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Декартово произведение двух множеств — это множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств.
Граф – это математический объект, который является совокупностью 2-ух множеств.
Множества точек и множества линий.
Точки – это вершины графа.
Линии – рёбра графа.
Вершины графа – это элемент графа, обозначающий объект любой природы, входящий в множество объектов, описываемое графом.
Изолированная вершина — вершина, не соединённая с другими вершинами ни дугами, ни рёбрами. однако такая вершина может иметь петли.
Степень вершины графа — количество рёбер графа инцидентных вершине.
Смежные вершины - вершины, соединённые ребром.
Ориентированный граф – это граф, рёбрам которого присвоено направление.
Граф без дуг (то есть неориентированный), без петель и кратных рёбер называется обыкновенным.
Взвешенным графом называется граф, вершинам и (или) рёбрам которого присвоены некоторые числа.
Петля – это ребро, соединяющее вершину саму с собой.
Функции одной переменной: Функции одной переменной – функции, зависящие только от одного аргумента.
· Тождественной нулем - называется функция, которая принимает значение нуля при любых значениях аргументов. Функция обозначается «0».
· Тождественной функцией - называется функция, которая принимает значения равные значению аргумента. Функция обозначается «х».
· Инверсия - функция принимающая значения противоположные значениям аргумента. Обозначается « 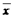 ».
».
· Тождественной единицей - называется, функция которая принимает значение единицы при любых значениях аргументов. Функция обозначается «1».
22. Область определения булевой функции: множество кортежей занятой длины.
Дизъюнкция нескольких элементарных конъюнкций называется дизъюнктивной нормальной формой, или ДНФ.
29. Конъюнкция нескольких элементарных дизъюнкцийназывается конъюнктивной нормальной формой, или КНФ.
Предикаты (логическая функция) - Предикатом называется функция, аргументы которой принимают значения из некоторого множества, а сама функция – значение 0 («ложь») или 1 («истина»).
Квантор — это общее название для логических операций, ограничивающих область истинности какого-либо предиката.
34. Квантор общности (всякий, каждый, любой, все ) - ∀
35. Квантор существования (некоторые, существует, найдется) - ∃
В науке рассуждения по аналогии применяются столь же широко, как и во всех других областях человеческой деятельности. Этому совершенно не мешает то, что аналогия дает не твердое знание, а только более или менее вероятное предположение.
37. Дедукция – логический переход от общего к частному;
38. Индуктивное умозаключение — метод рассуждения от частного к общему.
Ответы к математической логике
Понятие множества
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком.
Конечность множества
Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным.
Мощность множества
Мощностью множества А называется количество входящих в его состав различных элементов и обозначается через !А! которое имеет смысл для всех множеств, включая бесконечные.
Универсальное множество — в математике множество, содержащее все объекты, все множества и понятия.
5. Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø.
Дата: 2018-12-28, просмотров: 326.