Устойчивость динамической системы – это способность динамической системы возвращаться в исходное установившееся состояние после снятия внешних воздействий (возмущений).

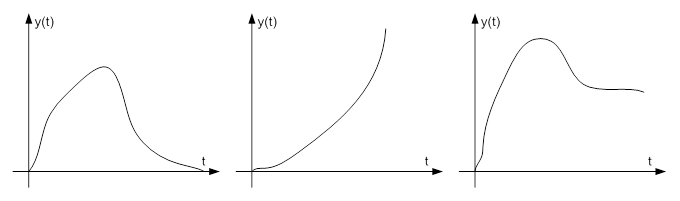
Линейные динамические системы можно разделить на устойчивые, неустойчивые и нейтральные. Нейтральной называется система, которая приходит при снятии возмущения в новое установившееся состояние. Об устойчивости системы можно судить, например, по виду ее импульсной переходной характеристики, характеристики для всех трех случаев приведены на рис. 13-1.

Рис. 13-1. ИПХ устойчивой, неустойчивой и нейтральной систем.

Существует несколько возможных причин неустойчивости динамических систем:

1. Наличие замкнутых контуров в системах управления и регулирования.
2. Наличие в системе положительных обратных связей.

В общем случае (то есть, для нелинейных систем) говорят об устойчивости движения системы, а не просто об устойчивости системы. В одной и той же системе могут быть и устойчивые и неустойчивые движения. В одной и той же системе могут быть и устойчивые и неустойчивые движения.

В настоящее время мы рассматриваем линейные системы, для которых устойчивость является внутренним свойством системы, она не зависит от вида возмущения или точки его приложения.

Устойчивая система – это система, которая после устранения воздействия на нее прекращает движение и самостоятельно переходит к некоторому установившемуся состоянию.

Импульсная переходная характеристика, отражающая устойчивость, выражается формулой:

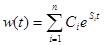.                                                          (13-1)

s₁...s_n – корни характеристического уравнения. Характеристическое уравнение – это знаменатель передаточной функции, приравненный к нулю:

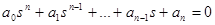.                                          (13-2)

Необходимое и достаточное условие устойчивости системы – все вещественные корни характеристического уравнения должны быть отрицательными, все комплексные корни должны иметь отрицательную вещественную часть. То есть, можно сказать, что система устойчива, если все корни характеристического уравнения лежат в левой комплексной полуплоскости.

Если имеется хотя бы один нулевой корень, система нейтральна.

Если имеется два чисто мнимых корня, то система находится на границе устойчивости.

Если имеется два нулевых корня или две пары мнимых корней, то система неустойчива.

Таким образом, нет необходимости искать сами корни, нужно только выяснить, где они расположены. Для этого применяются специальные правила под названием критерии устойчивости.

Критерий Рауса-Гурвица

Это алгебраический критерий, основанный на использовании коэффициентов характеристического уравнения (13-2). Нужно составить квадратную матрицу, также она называется матрицей Гурвица, это квадратная матрица n×n. Матрица имеет вид:

.

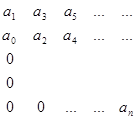Матрица состоит из коэффициентов характеристического уравнения, свободные места в матрице заполняются нулями. Далее последовательно вычисляются диагональные миноры, все диагональные миноры должны быть положительными, чтобы система была устойчива.

Если хотя бы один минор отрицателен, то система неустойчива.

Если коэффициенты характеристического уравнения знакопеременны, то система обязательно неустойчива, и матрицу можно не составлять.

Критерий Михайлова

Критерий Михайлова так же работает на основании характеристического уравнения и получаемого на его основе характеристического вектора или вектора Михайлова.

Система устойчива, если при изменении частоты от нуля до бесконечности годограф характеристического вектора, начинаясь на вещественной положительной полуоси проходит последовательно против часовой стрелки n квадрантов комплексной плоскости (где n – порядок характеристического уравнения, он же порядок системы). Говоря иначе, характеристический вектор должен совершать поворот против часовой стрелки на угол n*90.

Для получения характеристического вектора в характеристическом уравнении нужно заменить s на jω. Формула для характеристического вектора приводится ниже:

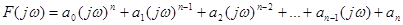.                      (13-3)

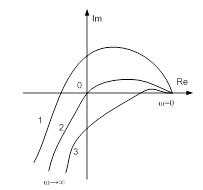
Если годограф проходит через начало координат, то система находится на границе устойчивости. Если годограф проходит не через то количество квадрантов или не в том порядке, то система неустойчива. Годографы для устойчивой системы, неустойчивой системы и системы на границе устойчивости показаны на рис. 13-2.

Рис. 13-2. Примеры годографов характеристического вектора для различных систем.

Годограф 1 соответствует устойчивой системе, годограф 2 соответствует системе на границе устойчивости, годограф 3 - неустойчивой системе.

Критерий Найквиста

Критерий Найквиста применяется для АСР с обратной связью и позволяет судить о поведении замкнутой АСР по поведению разомкнутой. Он формулируется следующим образом.

Если разомкнутый контур устойчив и годограф КЧХ разомкнутой АСР не охватывает точку на комплексной плоскости с координатами -1, j0, то после замыкания система сохранит устойчивость.

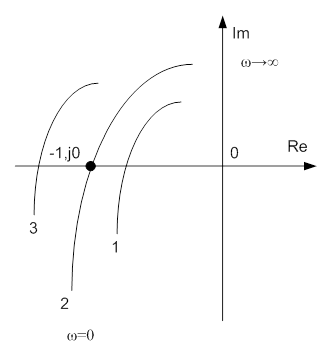
Если годограф проходит через эту точку, система находится на границе устойчивости. Если годограф охватывает эту точку, система неустойчива. Примеры годографов приведены на рис. 13-3.

Рис. 13-3. Примеры годографов КЧХ разомкнутой АСР.

Запас устойчивости