Часто в системном анализе при модельном подходе исследования может совершаться одна методическая ошибка, а именно, - построение корректных и адекватных моделей (подмоделей) подсистем системы и их логически корректная увязка не дает гарантий корректности построенной таким способом модели всей системы.

  Модель, построенная без учета связей системы со средой и ее поведения по отношению к этой среде, может часто лишь служить еще одним подтверждением теоремы Геделя, а точнее, ее следствия, утверждающего, что в сложной изолированной системе могут существовать истины и выводы, корректные в этой системе и некорректные вне ее.

  Наука моделирования состоит в разделении процесса моделирования (системы, модели) на этапы (подсистемы, подмодели), детальном изучении каждого этапа, взаимоотношений, связей, отношений между ними и затем эффективного описания их с максимально возможной степенью формализации и адекватности.

В случае нарушения этих правил получаем не модель системы, а модель "собственных и неполных знаний".

Моделирование рассматривается как особая форма эксперимента, эксперимента не над самим оригиналом, т.е.  простым или обычным экспериментом, а над копией  оригинала. Здесь важен изоморфизм систем оригинальной и модельной. Изоморфизм -  равенство, одинаковость, подобие.

Модели и моделирование применяются по основным направлениям:

• в обучении (как моделям, моделированию, так и самих моделей);
• в познании и разработке теории исследуемых систем;
• в прогнозировании (выходных данных, ситуаций, состояний системы);
• в управлении (системой в целом, отдельными ее подсистемами), в выработке управленческих решений и стратегий;
• в автоматизации (системы или ее отдельных подсистем).

Математическое и компьютерное моделирование

Классификация видов моделирования

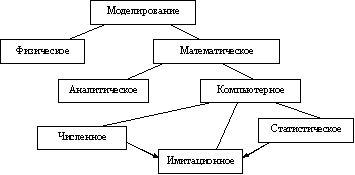
При физическом моделировании  используется сама система, либо подобная ей в виде макета, например, летательный аппарат в аэродинамической трубе.

Математическое моделирование есть  процесс установления соответствия реальной системе S математической модели M и исследование этой модели, позволяющее получить характеристики реальной системы.

При аналитическом моделировании процессы функционирования элементов записываются в виде математических соотношений (алгебраических, интегральных, дифференциальных, логических и др.).

  Аналитическая модель может быть исследована методами:

· аналитическими (устанавливаются явные зависимости, получаются, в основном, аналитические решения);

· численными (получаются приближенные решения);

· качественными (в явном виде можно найти некоторые свойства решения).

Компьютерное – математическое моделирование формулируется в виде алгоритма (программы для ЭВМ), что позволяет проводить над ней вычислительные эксперименты.

Численное моделирование  использует  методы вычислительной математики.

Статистическое моделирование использует  обработку данных о системе  с целью получения статистических характеристик системы.

Имитационное моделирование  воспроизводит на ЭВМ (имитирует) процесс  функционирования исследуемой системы, соблюдая логическую и временную последовательность протекания процессов, что позволяет узнать данные о состоянии системы или отдельных ее элементов в определенные моменты времени.

Применение математического моделирования позволяет исследовать объекты, реальные эксперименты над которыми затруднены или невозможны.

Экономический эффект при математическом  моделировании состоит в том, что  затраты на проектирование систем в среднем сокращаются в 50 раз.