Кинематика
Движение со связями.
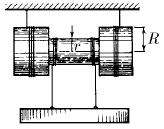Задача 38
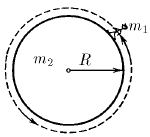
Угловая скорость катушки равна ω, радиус внутреннего цилиндра r, а радиус внешних цилиндров R. Каковы скорости оси катушки и груза относительно земли?
Ответ: 
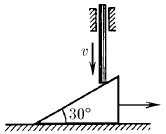Задача 39
На клине с углом α лежит монета. С каким наименьшим ускорением должен двигаться клин по горизонтальной плоскости, чтобы монета свободно падала вниз?
Ответ: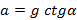 
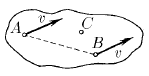Задача 40
Скорости точек A и B твердого тела равны v. Скорость точки С, находящейся в плоскости прямой AB и вектора v, равна u > v. Найдите проекцию скорости точки С на ось, перпендикулярную указанной плоскости.
Ответ: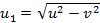 
Задача 41
Постройте траектории точек колеса, катящегося без проскальзывания по рельсу. Рассмотрите случаи когда точки находятся от оси колеса на расстоянии: r > R , r = R , r < R. Найдите ускорение этих точек, если ось колеса движется с постоянной скоростью v.
Ответ: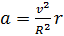 
Задача 42
Луна обращена к Земле постоянно одной стороной. Сколько оборотов совершит она вокруг своей оси за время полного оборота вокруг Земли?
Ответ: простой
Задача 43
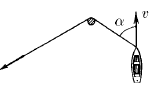Веревку, привязанную к лодке, тянут за свободный конец таким образом, чтобы она не провисала. Лодка движется с постоянной скоростью v, образуя в некоторый момент времени угол α с отрезком веревки, находящимся между столбом и лодкой. С какой скоростью нужно тянуть в этот момент времени свободный конец веревки?
Ответ: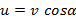 
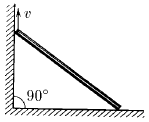Задача 44
Стержень длины L упирается своими концами в стороны прямого угла. Верхний конец стержня поднимают со скоростью v. Найдите, как зависит от времени скорость его нижнего конца. Начало отсчета времени считать моментом, когда верхний конец стержня находится в вершине прямого угла.
Ответ: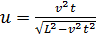 
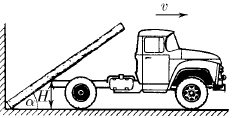Задача 45
Бревно, упираясь нижним своим концом в угол между стеной и землей, касается дна грузовика на высоте H от земли. Найдите угловую скорость бревна в зависимости от угла α между ним и горизонтом, если грузовик отъезжает от стены со скоростью v.
Ответ: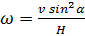 
Динамика.
Законы Ньютона.
Задача 46
Шайба, скользившая по льду, остановилась через время t = 5 с после удара о клюшку на расстоянии l = 20 м от места удара. Масса шайбы m = 100 г. Определите действовавшую на шайбу силу трения.
Ответ: 16Н
Задача 47
Два тела массы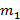 
и 
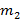связаны нитью, выдерживающей силу натяжения T. К телам приложены силы 
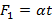и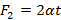 
, где α – постоянный коэффициент, а t – время действия силы. Определите, в какой момент времени нить порвется.
Ответ: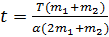 
Задача 48
Для подготовки к работе в условиях невесомости одетые в скафандры космонавты тренируются в воде. При этом сила тяжести, действующая на них, уравновешивается выталкивающей силой. В чем отличие такой «невесомости» от настоящей?
Ответ: тут думать надо
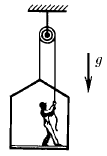Задача 49
Маляр работает в подвесной люльке. Ему понадобилось срочно подняться вверх. Он начинает тянуть за веревку с такой силой, что сила его давления на пол люльки уменьшилась до 400 Н. Масса люльки 12 кг. Масса маляра 72 кг. Чему равно ускорение люльки?
Ответ: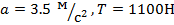 
Задача 50
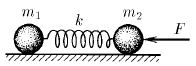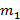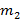Тела массы и соединены пружиной жесткости k. На тело массы 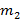действует постоянная сила F, направленная вдоль пружины к телу массы 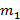. Найдите на сколько сжата пружина, если никаких других внешних сил нет, а колебания уже прекратились. Каким будет ускорение тел сразу же после прекращения действия силы F?
Ответ: 
Задача 51
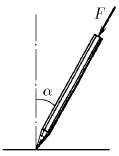Если нажимать пальцем на шариковую ручку, опирающуюся на твердую поверхность, одновременно наклоняя ее, то, пока ручка образует малый угол с перпендикуляром к поверхности, она будет следовать за пальцем (как шарнирно закрепленная). Как только угол наклона достигнет какого-то значения 
, она выскользнет из-под пальца, независимо от приложенной силы. Поэкспериментируйте и оцените коэффициент трения между шариком ручки и поверхностью, на которую она опирается.
Ответ: это ваш эксперимент
Задача 52
На горизонтальной доске лежит брусок массы m. Доску медленно наклоняют. Определите зависимость силы трения действующей на брусок, от угла наклона доски α. Коэффициент трения μ.
Ответ:
Задача 53
Через какое время скорость тела, которому сообщили вверх по наклонной плоскости скорость v, снова будет равна v? Коэффициент трения μ, угол между плоскостью и горизонтом α.
Ответ: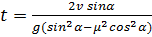 
Задача 54
На тело массы m, лежащее на горизонтальной плоскости, действует сила F под углом α к горизонту. Коэффициент трения μ. Найдите ускорение тела, если оно не отрывается от плоскости.
Ответ: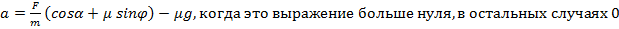 
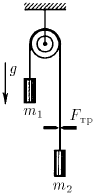Задача 55
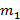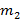Нить, перекинутая через блок с неподвижной осью, пропущена через щель. На концах нити подвешены грузы, масса которых и . Определите ускорения грузов, если при движении нити на нее со стороны щели действует постоянная сила трения 
.
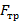Ответ: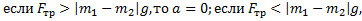 
Задача 56
Коэффициент трения шипованных шин на обледеневшей дороге в десять раз больше чем нешипованных. Во сколько раз нужно занижать скорость движения, чтобы длина тормозного пути оставалась прежней?
Ответ: готовьтесь к взрослой жизни, будущие водители=)
Задача 57
Спортивный автомобиль, трогаясь с места разгоняется до 72 км/ч за 5 с (быстрее невозможно в силу проскальзывания колес). Каков коэффициент трения между колесами и дорогой? Каким будет наименьший тормозной путь данного автомобиля при торможении с той же скорости?
Ответ: а вдруг вы купите спорткар?
Задача 58
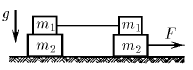На гладком горизонтальном столе расположена система грузов, изображенная на рисунке. Правый нижний груз тянут вдоль стола с силой F, как указано на рисунке. Коэффициент трения между грузами массы 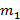и 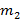равен μ. Найдите ускорение всех грузов системы.
Ответ: 
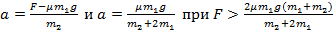
Задача 59
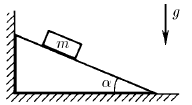Определите силу действующую на вертикальную стенку со стороны клина, если на него положили груз массы m. Угол при основании клина α. Коэффициент трения между грузом и клином μ. Трения между клином и полом нет.
Ответ: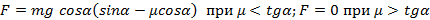 
Задача 60
Сила сопротивления воздуха действующая на велосипедиста пропорциональна квадрату скорости велосипедиста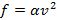 
. На горизонтальной дороге наибольшая скорость велосипедиста составляет примерно 20 м/с. Оцените коэффициент пропорциональности α, если масса велосипедиста вместе с велосипедом 70 кг, а коэффициент трения между колесами и дорогой 0,4.
Ответ: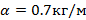 
Задача 61
Сила сопротивления жидкости или газа, пропорциональная квадрату скорости движущегося теля, связана с образованием вихрей вблизи поверхности этого тела. Сила сопротивления, пропорциональная скорости движущегося тела, связана с проскальзыванием слоев среды при обтекании ею этого теля. Оба явления всегда проходят одновременно. Почему тем не менее в тех или иных случаях можно принимать во внимание только один какой-либо вид сопротивления? По данным задач 22 и 23, решенных в классе, оцените, при каком значении произведения радиуса круглой капли на ее скорость оба вида сопротивления воздуха сравнимы по своему воздействию на движение капли.
Задача 62
Электроны, движущиеся по окружности любого радиуса вокруг заряженной нити, имеют одну и ту же скорость v. Масса электрона me. Как зависит сила, действующая со стороны нити на электрон, от расстояния между электроном и нитью? Опишите качественно начальный отрезок траектории, по которой будет двигаться электрон, если скорость его движении по окружности станет вдруг чуть меньше v? Чуть больше v?
Задача 63
Почему крепко засевший в бревне гвоздь проще вытащить, если при этом его вращать вокруг своей оси?
Ответ: потому
Задача 64
По наклонной плоскости скользят два тела одинаковой массы, связанные нитью. Сила натяжения нити T. Трения между одним телом и плоскостью нет. Определите силу трения между доской и другим телом.
Ответ: очевиден
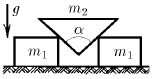Задача 65
Между двумя гладкими брусками массы 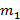каждый вставлен клин массы и 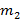с углом раствора α. Определите ускорение всех тел системы. Трения нет
Ответ: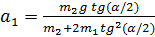 
; 
;
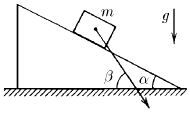Задача 66
На гладкой горизонтальной плоскости находится клин с углом раствора α. Тело массы m, положенное на клин, опускается с ускорением, направленным под углом β > α к горизонту. Определите массу клина.
Ответ: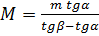 
Задача 67
Ускорение звезд, входящих в состав двойной звезды,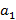 
и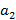 
. Какова масса второй звезды, если масса первой ?
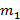Ответ: слишком просто
Задача 68
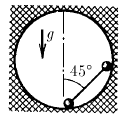
В сферическую полость положили гантель с шариками массы m и невесомым стержнем так, как это показано на рисунке. Определите силу давления шариков на стенки сразу после того, как гантель отпустили. Радиус шариков много меньше радиуса сферы.
Ответ: для верхнего mg/2, для нижнего 3mg/2
Задача 69
Два шарика массы m каждый связаны нитью длины l и движутся со скоростью v по горизонтальному столу в направлении, перпендикулярном связывающей их нити. Нить не провисает. Середина нити налетает на гвоздь вбитый в поверхность стола. Чему равна сила натяжения нити в этот момент?
Ответ: халява
Задача 70
К тяжелому шарику, подвешенному на нити длины l, подвешен другой тяжелый шарик на нити той же длины. При вращении шариков вокруг вертикальной оси, проходящей через верхнюю точку подвеса первого шарика, обе нити лежат в одной плоскости и составляют с вертикалью постоянные углы α и β. Найдите угловую скорость вращения шариков.
Ответ: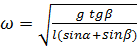 
Задача 71
Груз массы m, прикрепленный пружиной жесткости k к оси, движется вокруг этой оси по окружности радиуса R с угловой скоростью ω. Какова длина недеформированной пружины?
Ответ: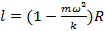 
;
Задача 72
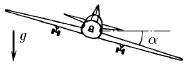Самолет совершает вираж, двигаясь по горизонтальной окружности радиуса R с постоянной скоростью v. Какой угол составляет плоскость крыла самолета с горизонтом?
Ответ: 
Задача 73
Горизонтальный диск начинают раскручивать вокруг своей оси с линейно возрастающей по времени угловой скоростью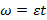 
. При какой угловой скорости тело, расположенное на расстоянии r от оси диска начнет соскальзывать с него, если коэффициент трения между ними равен μ?
Ответ: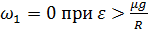 
; 
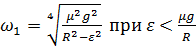
Задача 74
С какой максимальной скоростью может ехать по горизонтальной плоскости мотоциклист, описывая круг радиуса R, если коэффициент трения равен μ? На какой угол от вертикали он должен при этом отклониться? Во сколько раз увеличится максимально допустимая скорость мотоциклиста при движении по наклонному треку с углом наклона α к горизонту по сравнению с максимально допустимой скоростью при движении по горизонтальному треку при том же радиусе поворота и том же коэффициенте трения.
Ответ: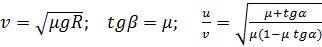 
Импульс. Центр масс.
Задача 75
Первоначально неподвижное тело, находящееся на горизонтальной плоскости, начали тянуть за привязанную к нему веревку с постоянной горизонтальной силой F. Через время Δt действие силы прекратилось. Какая сила трения действовала на тело во время его движения, если оно остановилось спустя время 3Δ t после начала движения?
Ответ: F тр = F /3
Задача 76
Космический корабль должен, изменив курс, двигаться с прежним по модулю импульсом p под углом α к первоначальному направлению. На какое наименьшее время нужно включить двигатель с силой тяги F и как при этом ориентировать ось двигателя?
Ответ: t = 2 pSin ( α /2)/ F , β = (π+α)/2
Задача 77
Сестры стоят на коньках на гладком льду. Старшая толкает младшую. Обе начинают катиться, но младшая с заметно большей скоростью, чем старшая. «Давай, теперь я тебя толкну», говорит младшая. Вопреки ее ожиданиям, она снова откатывается с большей скоростью, чем ее старшая сестра, причем во столько же большей, как в первый раз. Почему так происходит?
Задача 78
Человек решил бежать по резиновой ленте горизонтального транспортера, которая натянута на ролики, трения в осях которых нет. Останется ли человек на месте или будет двигаться относительно земли?
Задача 79
Снаряд разорвался в наивысшей точке траектории своего полета на расстоянии L по горизонтали от пушки на два одинаковых осколка. Один из них вернулся обратно по первоначальной траектории снаряда. Где упал второй осколок?
Ответ: 4 L
Задача 80
Артиллерист стреляет из пушки ядром массы m так, чтобы оно упало на неприятельский лагерь. На вылетевшее из пушки ядро садится барон Мюнхаузен, масса которого 5 m. Какую часть пути до неприятельского лагеря ему придется идти пешком?
Ответ: S / L = 35/36
Задача 81
Частица массы m 1, имеющая скорость v, налетела на покоящееся тело массы m 2 и отскочила от него со скоростью u под прямым углом к направлению первоначального движения. Какова скорость тела массы m 2?
Ответ: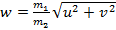 
Задача 82
Радиоактивное ядро распалось на три осколка массы m 1 , m 2 , m 3 имеющих взаимно перпендикулярные скорости v 1 , v 2 , v 3 соответственно. Какова была скорость ядра до распада?
Ответ: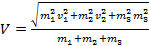 
Задача 83
Космонавт массы m 1 приближается к космическому кораблю массы m 2, с помощью легкого троса. Первоначально корабль и космонавт неподвижны, а расстояние между ними l. Какое расстояние пройдут корабль и космонавт до встречи?
Ответ: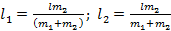 
Задача 84
Две заряженные частицы массы m и 2 m, имеющие равные по модулю импульсы, одновременно вылетают навстречу друг другу из точек A и B . Частицы взаимодействуют только друг с другом. По траектории частицы массы 2 m восстановите траекторию другой частицы.
Задача 85
Космическая станция представляет собой цилиндр радиуса R и массы m 2. Космонавт массы m 1 начал круговой обход станции по ее поверхности. Определите траекторию космонавта и траекторию центра станции. В начальный момент времени космонавт и станция неподвижны.
Задача 86
Где находится центр масс произвольной однородной трапеции? однородного круглого гардеробного номерка в виде диска с круглым не концентрическим отверстием (см. рис.)?
Задача 87
Для создания искусственной силы тяжести два отсека орбитальной станции (отношение масс 1:2) развели на расстояние R друг от друга и раскрутили вокруг их общего центра масс. Определите время полного оборота отсеков, если в более массивном отсеке искусственная сила тяжести в два раза меньше силы тяжести на Земле.
Ответ: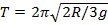 
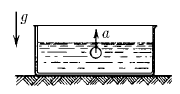Задача 88
В сосуде, наполненном водой плотности ρ, с ускорением a всплывает пузырек воздуха, объем которого V. Найдите силу давления со стороны сосуда на опору. Масса сосуда вместе с водой равна m.
Ответ: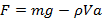 
Задача 89
На чаше весов прыгает N шариков массы m каждый. Какова средняя сила, действующая на чашу весов, если скорость шариков по модулю не меняется? Увеличивается или уменьшается эта сила, если после удара скорость каждого шарика будет уменьшаться?
Ответ: 
Задача 90
На чаше весов стоят песочные часы. Когда песок внизу, показания весов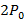 
. Вес песка равен 
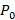. Часы переворачивают. Нарисуйте график зависимости показания весов от времени. Время падения каждой песчинки Δt, время протекания песка T.
Задача 91
С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально вверх со скоростью v? Масса змеи m, ее длина l.
Ответ: 
Статика
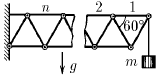
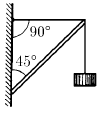Задача 147
К стене под углом 90° прикреплена балка. Через свободный конец балки перекинут трос, который закреплен к стене на одной высоте с со свободным концом балки. За второй конец троса подвешен груз массы m. Найдите силу действующую на балку со стороны троса. Трением пренебречь.
Ответ
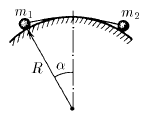Задача 148
Два груза небольшого размера соединены нитью длины l и лежат на цилиндрической гладкой поверхности радиуса R. При равновесии грузов угол между вертикалью и радиусом, проведенным к грузу массы 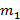, равен α. Найдите массу второго груза.
Ответ: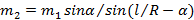 
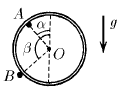Задача 149
Гладкий тонкий обруч массы m висит у стенки на одном гвозде (А) и опирается на другой (B). Радиус, проведенный к гвоздю А из центра обруча, образует угол α с вертикалью. Радиус, проведенный к гвоздю B, образует угол β с вертикалью. Найдите, с какой силой действует обруч на каждый гвоздь.
Ответ: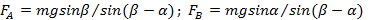 
Задача 150
На цилиндрический столб намотан один виток каната. Чтобы канат не скользил по столбу, когда его за один из концов тянут с силой F, другой конец каната достаточно удерживать с силой f. Как изменится удерживающая сила, если на столб намотано n витков? Витки каната не соприкасаются друг с другом.
Ответ: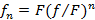 
Задача 151
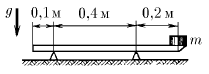Линейка массы 10 г лежит на двух опорах так, как это показано на рисунке. На один конец линейки положен груз. Какова масса груза, при которой возможно равновесие?
Ответ: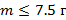 
Задача 152
Центр масс коромысла равноплечих весов находится ниже точки подвеса на расстоянии h от нее, а масса коромысла равна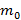 
. На концах коромысла, расстояние между которыми равно 2 L, на нитях подвешены одинаковые чашки. На сколько отличаются массы грузов, положенных на чашки, если коромысло отклонилось на угол α?
Ответ: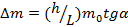 
Задача 153
Однородная балка длины l и массы m на расстоянии l /3 от конца имеет ось вращения. К концу балки присоединена пружина, прикрепленная к полу, и такая же пружина присоединена симметрично по другую сторону оси. При горизонтальном положении балки обе пружины не деформированы. Найдите силы, с которыми балка действует на ось и пружины. Деформации пружин малы, балка практически горизонтальна.
Ответ: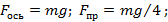 
Задача 154
Найдите силу натяжения нити, связывающей оси шарниров верхнего ромба легкой шарнирной подвески. Масса груза m.
Ответ: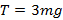 
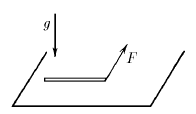
Задача 155
Однородный тонкий брусок массы m лежит на горизонтальной плоскости. Какой наименьший горизонтальной силой, приложенной к концу бруска по перпендикуляру к нему, его можно стронуть с места, если коэффициент трения между бруском и плоскостью равен µ?
Ответ: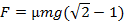 
Для олимпиадников:
· 
(156) К системе одинаковых стержней, соединенных шарнирами, подвешен груз массы m, как показано на рисунке. Определите силу, растягивающую n-й верхний горизонтальный стержень.
Ответ:
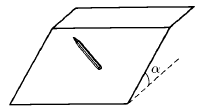
· (157) На парту с углом наклона поверхности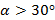 
кладут шестигранный карандаш так, чтобы он не скатился вниз и не скользил. При каком наименьшем угле между осью карандаша и горизонтальным краем парты это возможно?
Ответ
Механика жидкости.
Давление жидкости.
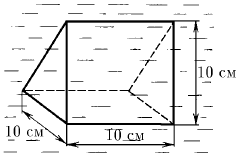Задача 158
В жидкости находится прямоугольная призма, размеры которой показаны на рисунке. Найдите сумму сил, действующих на переднюю и нижнюю грани призмы, если давление жидкости равно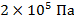 
. Чему равна сумма сил, действующих на призму?
Ответ: очевиден
Задача 159
В трубе радиуса r находится поршень, продольное сечение которого показано на рисунке, угол при основании α. Давление жидкости с обеих сторон поршня одинаково и равно P. Найдите сумму сил, действующих на поршень в направлении оси трубы. При каком значении коэффициента трения между поршнем и трубой, поршень не будет двигаться?
Ответ: очевиден
Задача 160
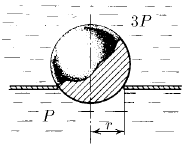
Шар перекрывает отверстие радиуса r в плоской стенке, разделяющей жидкости, давление которых равно 3P и P. С какой силой прижимается шар к отверстию?
Ответ: тоже слишком просто для наличия ответа
Задача 161
Почему сосиска в кипятке лопается вдоль, а не поперек?
Ответ: не могу подсказать
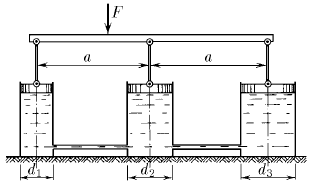
Задача 162
Три сообщающихся сосуда с водой прикрыты поршнями. К поршням шарнирно прикреплена на вертикальных стержнях горизонтальная палка. В каком месте нужно приложить к палке силу F, чтобы она осталась горизонтальной? Диаметры сосудов и расстояния между ними даны на рисунке.
Ответ: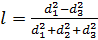 
слева от центра палки
Задача 163
В сосуде, дно которого образует угол α с горизонтом, стоит куб с ребром a, сделанный из материала плотности ρ. Верхнее ребро куба находится на глубине h. Жидкость под основание куба не подтекает. Атмосферное давление P. Плотность жидкости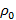 
. Найдите силу, с которой куб действует на дно сосуда.
Ответ: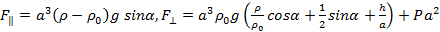 
Задача 164
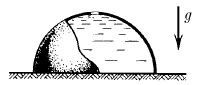
В полусферический колокол с внутренним радиусом R, края которого плотно прилегают к поверхности стола, наливают через отверстие вверху жидкость плотности ρ. Когда жидкость доходит до отверстия, она приподнимает колокол и начинает из-под него течь. Найдите массу колокола.
Ответ: 
Задача 165
Докажите, что в двух сообщающихся сосудах жидкость в поле тяжести имеет минимальную потенциальную энергию, когда уровни жидкости в обоих сосудах находятся на одной высоте.
Задача 166
Найдите давление на расстоянии r от центра жидкой планеты радиуса R, если жидкость имеет плотность ρ. Чему равно давление в центре планеты? Гравитационная постоянная равна G.
Ответ: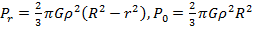 
Задача 167
В сосуде с жидкостью находится газовый пузырь. Поля тяжести нет. Сосуд начинает двигаться с постоянным ускорением. Куда начнет двигаться пузырь?
Ответ: очевидно
Задача 168
Найдите форму поверхности жидкости в вертикально расположенном цилиндрическом стакане, который вращается вместе с жидкостью вокруг своей оси с угловой скоростью ω.
Ответ: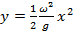 
Закон Архимеда.
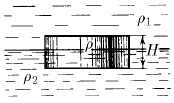Задача 169
На границе раздела двух жидкостей плотности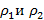 
плавает шайба плотности ρ ( 
). Высота шайбы H. Определите глубину ее погружения в нижнюю жидкость.
Ответ: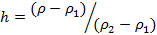 
Задача 170
Тело в воде весит в три раза меньше, чем в воздухе, чему равна плотность тела?
Ответ: просто
Задача 171
К коромыслу весов подвешены два груза равной массы. Если один из грузов поместить в жидкость плотности 
, а другой в жидкость плотности 
, то равновесие сохраняется. Найдите соотношение плотностей грузов.
Ответ: элементарно
Задача 172
В сообщающиеся сосуды диаметра 
налита жидкость плотности ρ. На сколько поднимется уровень жидкости в сосудах, если в один из сосудов положить тело массы m из материала, плотность которого меньше ρ?
Ответ: 
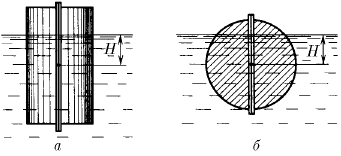Задача 173
Как зависит сила, прижимающая друг к другу два одинаковых полуцилиндра плавающего батискафа, от глубины его погружения H, если он плавает на поверхности жидкости так, как это показано на рисунках а и б? Радиус батискафа R, длина L, плотность жидкости ρ.
Ответ: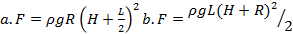 
Задача 174
Докажите, что сила, с которой прижимаются половины плавающего батискафа друг к друга, не зависит от наклона плоскости соприкосновения полусфер батискафа, если он полностью погружен в воду.
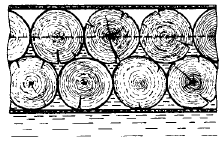Задача 175
Определите минимальную силу натяжения двух канатов, связывающих широкий плот, состоящий из двух слоев бревен. Масса каждого бревна m. Верхний слой бревен погружен в воду наполовину. 4.2.20
Ответ: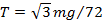 
Задача 176
Какое количество теплоты выделится в водоеме при всплывании в нем воздушного пузыря радиуса R с глубины H? Плотность жидкости ρ.
Ответ: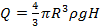 
Задача 177
Какую минимальную работу нужно произвести, чтобы поднять со дна моря на борт судна батисферу радиуса R и массы m? Глубина моря H, высота борта судна h. Плотность морской воды ρ.
Задача 178
Цилиндрический космический корабль радиуса R вращается вокруг своей оси с угловой скоростью ω. Бассейн в корабле имеет глубину H, а дном бассейна служит боковая стенка корабля. Определите плотность плавающей в бассейне палочки длины 
, если из воды выступает ее верхняя часть длины Δ.
Ответ: 
Задача 179
Вертикальный цилиндрический сосуд радиуса R, частично наполненный жидкостью, вращается вокруг своей оси. К боковой стенке сосуда на нити длины l привязан воздушный шарик радиуса r; во время вращения нить образует со стенкой угол α. Определите угловую скорость вращения сосуда.
Ответ: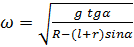 
Задача 180
Молекула жидкости состоит из двух слабо связанных групп атомов. Объем этих групп одинаков, их массы равны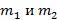 
. При вращении жидкости в центрифуге радиуса R с угловой скоростью, большей ω, молекулы начинают распадаться. Оцените силу связи групп атомов.
Ответ: 
Течение идеальной жидкости.
Задача 181
Насос должен подавать ежесекундно объем воды V на высоту h по трубе постоянного сечения S. Какова должна быть мощность насоса? Плотность воды ρ.
Ответ: 
Задача 182
Насос представляет собой расположенный горизонтально цилиндр с поршнем площади S и выходным отверстием площади s, расположенным на оси цилиндра. Определите скорость истечения струи жидкости из насоса, если поршень под действием силы F перемещается с постоянной скоростью. Плотность жидкости ρ.
Ответ: 
Задача 183
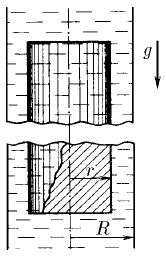Плита массы m удерживается на месте в горизонтальном положении N струями жидкости плотности ρ, бьющими вертикально вверх. Площадь каждого отверстия S. Скорость жидкости на выходе из отверстий v. На какой высоте над отверстиями удерживается плита, если, достигнув плиты, жидкость разлетается от нее в горизонтальной плоскости?
Ответ: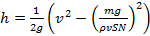 
Задача 184
С каким ускорением будет двигаться длинное цилиндрическое тело плотности ρ и радиуса r вдоль оси вертикального высокого цилиндрического сосуда радиуса R, заполненного жидкостью плотности 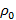? Чему равна разность давлений на верхнее и нижнее основания тела, если его длина равна h?
Ответ: 
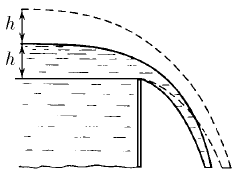Задача 185
Во сколько раз увеличится сброс воды через широкую плотину, если высота уровня воды над кромкой возрастет в два раза?
Ответ: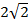 
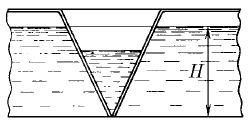Задача 186
Вода вытекает из широкого сосуда через треугольный вырез в его стенке. Во сколько раз уменьшится скорость понижения уровня жидкости при изменении высоты ее уровня от H до h?
Ответ: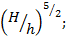 
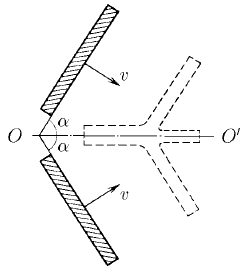Задача 187
Две широкие металлические пластины, расположенные под углом 2α друг к другу, движутся со скоростью v по нормали к своей поверхности. Найдите скорость струй, возникающих при столкновении пластин, рассматривая движение металла как движение идеальной жидкости.
Ответ: 
Задача 188
Определите форму стационарной струи, сформировавшейся после столкновения двух струй радиуса R и r, которые двигались навстречу друг другу с одинаковой скоростью.
Ответ: 
Течение вязкой жидкости.
Задача 189
Пространство между двумя параллельными плоскостями заполнено жидкостью вязкости η. Одна из плоскостей движется со скоростью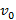 
, другая покоится. Расстояние между плоскостями h. Найдите:
а. распределение скорости жидкости между плоскостями (или, хотя бы градиент);
б. силу вязкого трения, действующую на единицу площади каждой из плоскостей.
Ответ: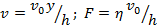 
;
Задача 190
Из вертикально расположенной трубки, заполненной вязкой жидкостью, через время T вытекла половина жидкости. Через какое время вытечет оставшаяся часть жидкости?
Ответ: думаем
Задача 191
Пространство между валом радиуса r, вращающегося вокруг своей оси и неподвижной соосной с валом трубой радиуса R заполнено жидкостью вязкости η. Момент сил, действующих на единицу длины вала, равен M. Определите зависимость от расстояния до оси вала:
а. градиента угловой скорости жидкости;
б. угловой скорости жидкости. Угловую скорость вала.
Ответ: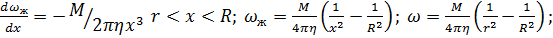 
Капиллярные явления.
Задача 200
Определите максимальный радиус капилляров дерева на высоте 10 м. Вода полностью смачивает капилляры.
Ответ: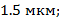 
Задача 201
Жидкость в длинном капилляре поднимается на высоту h. Определите радиус кривизны мениска в коротком капилляре, длина которого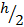 
. Радиус обоих капилляров r, краевой угол θ.
Ответ: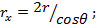 
Задача 202
Куда будет двигаться капля смачивающей и несмачивающей жидкости в горизонтально расположенном коническом капилляре?
Ответ: думаем;
Задача 203
На какую высоту поднимается жидкость по вертикальному коническому капилляру с углом при вершине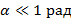 
? Плотность жидкости ρ, ее поверхностное натяжение σ, высота капилляра H. Жидкость полностью смачивает капилляр.
Ответ: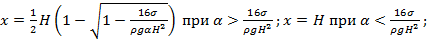 
Молекулярная физика.
Тепловое движение частиц.
Задача 204
Оцените среднюю кинетическую энергию и среднеквадратичную скорость частичек тумана диаметра 10 мкм, находящихся в воздухе при температуре 5 °С.
Ответ: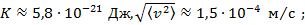 
Задача 205
В секции сосуда находится смесь гелия с водородом. Давление водорода и гелия одинаково. В другой секции сосуда (назовем ее второй) находится вакуум. На короткое время в перегородке открывают отверстие. Определите отношение давления гелия к давлению водорода во второй секции сосуда.
Ответ: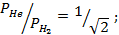 
Задача 206
Из сосуда через отверстие в стенке вытекает за время 
половина разреженного газа. За какое время вытекла бы половина этого же газа, если бы все размеры сосуда, в том числе размеры отверстия, были в n раз больше?
Ответ: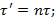 
Кинематика
Движение с постоянной скоростью.
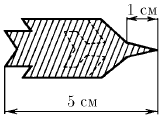Задача 1
На рисунке приведена «смазанная фотография» летящего самолета. Длина самолета 30 м, длина его носового обтекателя 10 м. Определите по этой фотографии скорость самолета. Время выдержки затвора фотоаппарата равна 0,1 с. Форма самолета в плане изображена штриховой линией.
Ответ: 200 м/с
Задача 2
Счетчики 
и 
регистрирующие момент прихода γ-кванта, расположены на расстоянии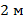 
друг от друга. В некоторой точке между ними произошел распад 
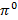-мезона на два γ-кванта. Найдите положение этой точки, если счетчик 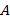зарегистрировал γ-квант на 
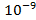с позднее, чем счетчик 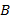. Скорость света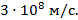 
Ответ: 1,15 м от счетчика А
Задача 3
Спортсмены бегут колонной длины l со скоростью v. Навстречу им бежит тренер со скоростью u < v. Каждый спортсмен, поравнявшись с тренером, разворачивается и начинает бежать в обратную сторону с той же по модулю скоростью. Какова будет длина колонны, когда развернутся все спортсмены?
Ответ: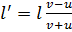 
Задача 4
Из взрывчатого вещества нужно изготовить такую тонкую коническую оболочку, ось которой вертикальна, чтобы при подрыве ее с вершины продукты взрыва одновременно ударили по горизонтально расположенной плите. Скорость детонации взрывчатого вещества равна v, скорость разлета продуктов взрыва равна u < v. Какой угол между осью конуса и образующей нужно выбрать?
Ответ: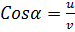 
Задача 5
Сверхзвуковой самолет летит горизонтально. Два микрофона, находящиеся на одной вертикали на расстоянии l друг от друга, зарегистрировали приход звука от самолета, пролетавшего над микрофонами с запаздыванием по времени в ∆ t. Скорость звука в воздухе c. Какова скорость самолета?
Ответ: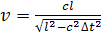 
Задача 6
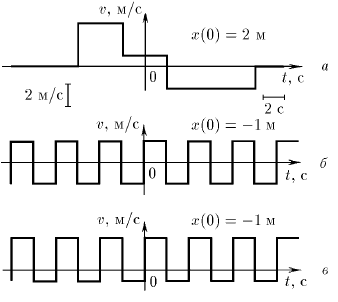
По графикам зависимости скорости от времени постройте графики зависимости координаты от времени. В случаях б и в найдите среднюю скорость за большой промежуток времени.
Задача 7
Частица движется в одной плоскости. По графикам зависимости проекций 
и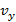 
скорости постройте траекторию частицы, если x (0) = 2 м, y (0) = 1 м.
Задача 8
Уголковый отражатель, установленный на луноходе, представляет собой три взаимно перпендикулярных зеркала. Если на отражатель падает свет скорость которого c = (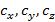 
), то какие составляющие будет иметь скорость света после отражения от зеркала, находящегося в плоскости yOz? После отражения от всех трех зеркал?
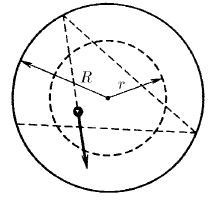
Задача 9
Внутри закрепленного гладкостенного цилиндра радиуса R летает маленький шарик, упруго отражаясь от стенок так, что минимальное расстояние от него до оси цилиндра равно h. Какую долю времени шарик находится на расстоянии от оси цилиндра, меньшем r, но большем h?
Ответ: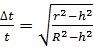 
Дата: 2018-12-28, просмотров: 415.
