МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНБАССКАЯ АГРАРНАЯ АКАДЕМИЯ»
Кафедра «Математики, физики и информационных технологий»
 |
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ДЛЯ ПРОВЕДЕНИЯ ПРАКТИЧЕСКИХ И СЕМИНАРСКИХ ЗАНЯТИЙ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
«Физика»
для студентов направления подготовки: 36.03.02 Зоотехния
35.03.04 Агрономия 35.03.05 Садоводство 35.03.03 Агрохимия и
агропочвоведение
Профиль: Зоотехния, Агрономия, Садоводство, Агрохимия и
агропочвоведение
Макеевка, 2017 г.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНБАССКАЯ АГРАРНАЯ АКАДЕМИЯ»
Кафедра «Математики, физики и информационных технологий»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ДЛЯ ПРОВЕДЕНИЯ ПРАКТИЧЕСКИХ И СЕМИНАРСКИХ ЗАНЯТИЙ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
«Физика»
для студентов направления подготовки: 36.03.02 Зоотехния
35.03.04 Агрономия 35.03.05 Садоводство 35.03.03 Агрохимия и
агропочвоведение
Профиль: Зоотехния, Агрономия, Садоводство, Агрохимия и
агропочвоведение
Макеевка, 2017 г.
УДК 657
Дулин М. А. Методические рекомендации для проведения практических и семинарских занятий по учебной дисциплине «Физика»» для студентов направления подготовки: 36.03.02 Зоотехния 35.03.04 Агрономия 35.03.05 Садоводство 35.03.03 Агрохимия и агропочвоведение образовательного уровня бакалавриат всех форм обучения –Дулин М. А Макеевка: ДОНАГРА, 2017. – с.
Рецензенты:
Александрова О. В. , кандидат физико-математических наук, доцент, доцент кафедры «Математики, физики и информационных технологий»
Маевская Н. В.., кандидат наук по гос. управлению, доцент, доцент кафедры
Финансов и бухгалтерского учета
Методические рекомендации составлены с целью организации практических и семинарских занятий по учебной дисциплине «Физика». Содержат теоретические вопросы для обсуждения, практические задания, задачи, кейсы, а также методики проведения занятий по дисциплине с помощью интерактивных методов обучения. Предложенные задания закрепляют полученные студентами теоретические знания, позволяют им освоить навыки проведения аудиторской проверки и изучить аудиторские процедуры, применяемые на каждом участке учета. Предназначены для студентов всех профилей направления подготовки 36.03.02 Зоотехния
35.03.04 Агрономия 35.03.05 Садоводство 35.03.03 Агрохимия и
агропочвоведение.
Рассмотрено на заседании предметно-методической комиссии кафедры
Математики, физики и информационных технологий
Протокол № от “ ” 2017 года
Утверждено на заседании кафедры
Математики, физики и информационных технологий
Протокол № от “ ” 2017 года
Рекомендовано к использованию в учебном процессе Решением Учебно-методического совета ДОНАГРА
Протокол № 5 от “15” октября 2017 года
© ДОНАГРА, 2017
Темы семинарских занятий и их содержание
Раздел 1. Механика, молекулярная физика и термодинамика
Практическое занятие Тема 1.1. Кинематика поступательного и вращательного движения.
Вопросы к обсуждению:
1. Материальная точка, система отчета, виды механического движения, пространство и время .
2. Скорость и ускорение.
3. Кинематика вращательного движения.
4. Связь между линейными и угловыми величинами.
Практическое занятие Тема 1.2. Динамика поступательного и вращательного движения.
Вопросы к обсуждению:
1. Первый закон Ньютона. Принцип относительности Галилея
2. Второй закон Ньютона.
3. Третий закон Ньютона.
4. Динамика вращательного движения. Момент силы. Момент инерции .
Практическое занятие Тема 1.3. Законы сохранения в механике
Вопросы к обсуждению:
1. Силы внутренние и внешние. Закон сохранения импульса.
2. Закон сохранения полной механической энергии.
Раздел 2. Электромагнитное взаимодействие и волны.
Примеры решения задач.
Пример 1
Точка двигалась в течение времени: t1=15с - со скоростью V1=5м/с; t2=10с - со скоростью V2=8м/с и t3=6с - со скоростью V3=20м/с. Определить среднюю путевую скорость точки.
Дано: Решение:
| t1=15с V1=5м/с t2=10с V2=8м/c t3=6с V3=20м/с | Средняя скорость движения на всем пути равна:
где:
Определим расстояния, пройденные за каждый промежуток |
| Vср=? |
времени: 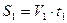 ;
; 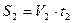
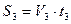
Время всего движения будет равно:
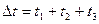
Подставим в формулу средней скорости:
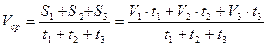
Выведем единицу измерения:
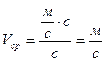
Рассчитаем численное значение:
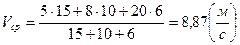
Ответ: Средняя путевая скорость движения материальной точки равна Vср=8,87 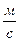 .
.
Пример 2
из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через Δt=2с после первой. Первая точка двигалась с начальной скоростью V01=1м/с и ускорением а1=2 м/с2,вторая - с начальной скоростью V2=10м/с и ускорением а2=1 м/с2. через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?
Дано: Решение:
| V01=1м/с а1=2 м/с2 Δt=2с V02=10м/с а2=1 м/с2 | Запишем уравнение движения материальной точки в векторном виде:
Т.к. точки движутся вдоль одной прямой, векторное уравнение можно спроектировать на направление этой прямой, и для каждой |
| t=? S=? |
точки будем иметь: 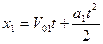
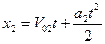
В момент встречи точек координаты x1= x2 . Время движения первой точки t1, второй - t2= t1- Δt.
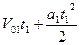
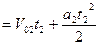
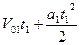
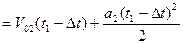
Преобразуем это уравнение
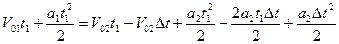
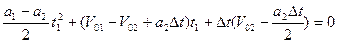
Для удобства решения этого уравнения подставим численные значения, получим:

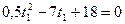
Решая это уравнение, определим значения времени встречи:
t1=3,4c; t2=10,6c.
Определим координаты места встречи:
S1= 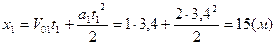
S2= 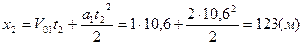
Проверим единицу измерения:
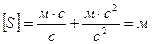
Ответ: встреча двух точек произойдет дважды: в момент времени t1=3,4c, S1=15м и в момент времени t2=10,6c, S2=123м.
Пример 3.
С балкона бросили мячик вертикально вверх с начальной скоростью 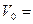 5м/с. Через время t=2с мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю.
5м/с. Через время t=2с мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю.
Дано: Решение:
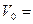 5м/с
t =2с 5м/с
t =2с
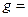 10м/с2 10м/с2
| Будем рассматривать движение мячика как движение материальной точки. Запишем уравнение движения и формулу изменения скорости в векторном виде:
|
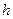 =?
V1=? =?
V1=?
|
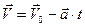 (2)
(2)
Изобразим движение материальной точки на рис.1. Так как точка 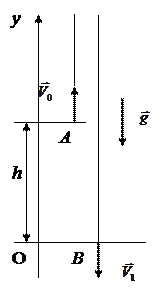 движется в гравитационном поле, на нее действует ускорение силы тяжести
движется в гравитационном поле, на нее действует ускорение силы тяжести 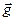 . Спроектируем уравнения (1) и (2) на ось Оу:
. Спроектируем уравнения (1) и (2) на ось Оу:
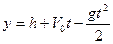 (3)
(3)
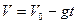 (4)
(4)
Эти уравнения описывают движение в любой точке траектории, значит и в точке В. Здесь будут выполняться следующие граничные условия: момент времени 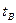 = t,
= t, 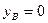 ,
, 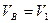 ,
,
Подставим в уравнения (3) и (4).
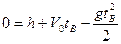
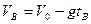
Решая эти уравнения, получим:
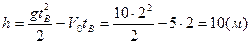
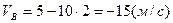
Рис.1 Знак «-» обозначает, что вектор скорости в т.в направлен противоположно оси Оу.
Проверим единицу измерения:
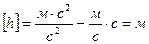
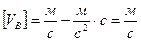
Ответ: высота балкона над землей 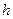 =10м; скорость мяча в момент удара о землю
=10м; скорость мяча в момент удара о землю
V1= -15м/с.
Пример 4
Движение двух материальных точек выражаются уравнениями 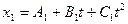 и
и 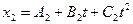 , где А1=20м; А2=2м; В1= В2 =2м/с; С1= -4м/с2 и С2= 0,5м/с2. В какой момент времени скорости этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент.
, где А1=20м; А2=2м; В1= В2 =2м/с; С1= -4м/с2 и С2= 0,5м/с2. В какой момент времени скорости этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент.
Дано: Решение:
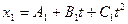
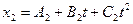 А1=20м
А2=2м
В1= 20м/с
В2 =2м/с
С1= -4м/с2
С2= 0,5м/с2
V1= V2
А1=20м
А2=2м
В1= 20м/с
В2 =2м/с
С1= -4м/с2
С2= 0,5м/с2
V1= V2
| Мгновенная скорость движения точки определяется как производная от х по времени:
или с соответствующими коэффициентами:
Используем условие V1= V2 и определим момент времени, для которого это условие выполняется:
Отсюда 9t=18, то есть t=2 с. Проверим единицу измерения, для этого в полученную формулу (1) подставим соответствующие единицы измерения: |
 =?
V1=? V2=?
а1=? а2=? =?
V1=? V2=?
а1=? а2=?
|
м/с -м/с2∙[t]= м/с+м/с2∙[t] м/с= м/с2∙[t] 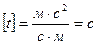
Подставим значение времени в формулу скорости и проведем вычисления, тогда
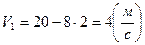
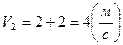 .
.
Выведем единицу измерения: 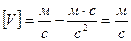 .
.
Чтобы определить ускорения точек в этот момент времени, возьмем вторую производную от х по времени: 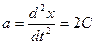 . Подставим соответствующие значения, получим:
. Подставим соответствующие значения, получим:
а1= -4м/с2; а2=0,5м/с2.
Ответ: скорости точек будут одинаковыми и равными V1=V2=4м/с в момент времени t=2с, ускорения точек для этого момента равны: а1= -4м/ с2; а2=0,5м/с2.
Пример 5
Одно тело свободно падает с высоты 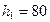 м. Одновременно с ним другое тело брошено вертикально вверх с высоты
м. Одновременно с ним другое тело брошено вертикально вверх с высоты 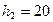 м над землей. Какой должна быть начальная скорость второго тела, чтобы оба тела упали одновременно?
м над землей. Какой должна быть начальная скорость второго тела, чтобы оба тела упали одновременно?
Дано: Решение:
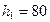 м м
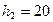 м м
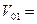 0
g=10м/с2 0
g=10м/с2
| Запишем уравнение движения и формулу изменения скорости в векторном виде:
Изобразим движение тел на рис.2. Так как тела движутся в |
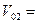 ? ?
|
поле сил притяжения Земли, на них действует ускорение силы тяжести 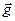 . Спроектируем уравнения (1) и (2) на ось Оу для первого и второго тел:
. Спроектируем уравнения (1) и (2) на ось Оу для первого и второго тел:
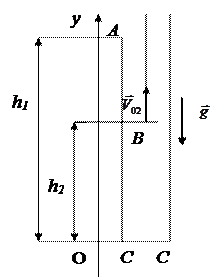 первое тело свободно падает с высоты
первое тело свободно падает с высоты 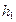 и его начальная скорость равна нулю
и его начальная скорость равна нулю
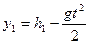 (3)
(3)
Второе тело подброшено вертикально вверх с начальной скоростью 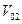
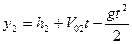 (4)
(4)
Эти уравнения описывают движение в любой точке траектории, значит, и в точке с. Здесь будут выполняться следующие граничные условия:
момент времени 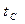 ,
, 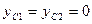 .
.
Подставим в уравнения (3) и (4).
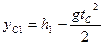
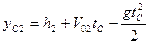
Рис.2. Решая эти уравнения, получим:
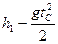 =
= 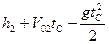
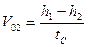 (5)
(5)
Момент времени 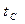 определим из соотношения:
определим из соотношения: 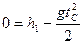
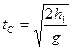
Подставим в (5) 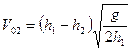
Рассчитаем численное значение:
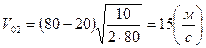
Проверим единицу измерения:
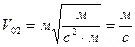
Ответ: начальная скорость второго тела должна быть равна 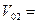 15м/с.
15м/с.
Контрольная работа 1
101. Тело брошено вертикально вверх с начальной скоростью υо = 4 м/с. Когда оно достигло верхней точки полета, из того же начального пункта, с той же начальной скоростью υо вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
102. Материальная точка движется прямолинейно с ускорением а = 5 см/с2. Определить, на сколько путь, пройденный точкой в n – ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять υо =0.
103. Две автомашины движутся по дорогам, угол между которыми - α = 60о. Скорость автомашин υ1= 54 км/ч и υ2 = 72 км/ч . С какой скоростью υ удаляются машины одна от другой?
104. Материальная точка движется прямолинейно с начальной скоростью υо =10м/с и постоянным ускорением а = -5 м/с 2.Определить, во сколько раз путь ∆s, пройденный материальной точкой, будет превышать модуль ее перемещения ∆r спустя t = 5 с после начала отсчета времени.
105. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью υ1= 18 км/ч. Далее половину оставшегося времени он ехал со скоростью υ2 = 22 км/ч, после чего до конечного пункта он шел пешком со скоростью υ3= 5 км/ч . Определить среднюю скорость  велосипедиста.
велосипедиста.
106. Тело брошено под углом α = 30о к горизонту со скоростью υо = 20 м/с. Каковы будут нормальное an и тангенциальное аτ ускорения тела через время t = 1 с после начала движения ?
107. Материальная точка движется по окружности с постоянной угловой скоростью ω = π/6 рад/с. Во сколько раз путь ∆s, пройденный точкой за время t = 4 с, будет больше модуля ее перемещения ∆r? Принять, что в момент начала отсчета времени радиус-вектор r ,задающий положение точки на окружности, относительно исходного положения был повернут на угол φ о = π/3 рад.
108. Материальная точка движется в плоскости ху согласно уравнениям х =А1 +B1t+ C1t2 и у =А2 +B2t+ C2t2 , где В1 = 7 м/с, C1= -2 м/с2 , В2 =-1 м/с, C2= 0,2 м/с2.Найти модули скорости и ускорения точки в момент времени t = 4 с.
109. По краю равномерно вращающейся с угловой скоростью ω = 1рад/с платформы идет человек и обходит платформу за время t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R=2 м.
110. Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением ε. Определить тангенциальное ускорение аτ точки, если известно, что за время t = 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение an = 2,7 м/с 2.
111. При горизонтальном полете со скоростью υ = 250 м/с снаряд массой m = 10 кг разорвался на две части. Большая часть массой m1= 7 кг получила скорость u1= 400 м/с в направлении полета снаряда. Определить модуль и направление скорости u2меньшей части снаряда.
112. С тележки, свободно движущейся по горизонтальному пути со скоростью υ1= 3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной u1= 4 м/с. Определить горизонтальную составляющую скорости u2х человека при прыжке относительно тележки. Масса тележки m1= 210 кг, масса человека m2= 70 кг.
113. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α = 30о к линии горизонта. Определить скорость u2 отката платформы, если снаряд вылетает со скоростью u1= 480 м/с. Масса платформы с орудием и снарядами m2= 18 т, масса снаряда m1= 60 кг.
114. Человек массой m1 = 70 кг, бегущий со скоростью υ1 = 6 км/ч, догоняет тележку массой m2 = 190 кг, движущуюся со скоростью υ2 = 3,6 км/ч, и вскакивает на нее . С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
115. Конькобежец, стоя на коньках на льду, бросает камень массой m1= 2,5 кг под углом α = 30о к горизонту со скоростью υ = 10 м/с. Какова будет начальная скорость υо движения конькобежца, если масса его m2= 60 кг? Перемещением конькобежца во время броска пренебречь.
116. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m1= 70 кг, масса доски m2= 20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) υ = 1м/с? Массой колес и трением пренебречь.
117. Снаряд, летевший со скоростью υ = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет30% от массы снаряда, полетел в противоположном направлении со скоростью u1= 150 м/с. Определить скорость u2 большего осколка.
118. Две одинаковые лодки массами m = 200 кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями υ = 1 м/с. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами m1= 30 кг. Определить скорости u1и u2лодок после перебрасывания грузов.
119. На сколько переместится относительно берега лодка l = 3,5 м и массой m1= 200 кг, если стоящий на корме человек массой m2= 80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.
120. Лодка длиной l = 3 м и массой m = 120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m1= 60 кг и m2= 90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?
121. В деревянный шар массой m1= 8 кг, подвешенный на нити длиной l = 1,8 м, попадает горизонтально летящая пуля массой m2= 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол α = 3о? Размером шара пренебречь. Удар пули считать прямым, центральным.
122. По небольшому куску мягкого железа, лежащему на наковальне массой m1= 300 кг, ударяет молот массойm2= 8 кг. Определить к.п.д. η удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа..
123. Шар массой m1= 1 кг движется со скоростьюυ1 = 4 м/с и сталкивается с шаром массой m2= 2 кг , движущимся навстречу ему со скоростью υ2 = 3 м/с. Каковы скорости u1и u2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
124. Шар массой m1= 3 кг движется со скоростьюυ1 = 2 м/с и сталкивается с покоящимся шаром массой m2= 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
125. Определить к.п.д. η неупругого удара бойка массой m1= 0,5 т, падающего на сваю массой m2= 120 кг. Полезной считать энергию, затраченную на вбивание сваи.
126. Шар массой m1= 4 кг движется со скоростью υ1 = 5 м/с и сталкивается с шаром массой m2= 6 кг, который движется ему навстречу со скоростью υ2 = 2 м/с. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
127. Из ствола автоматического пистолета вылетела пуля массой m1= 10 г со скоростью υ = 300 м/с Затвор пистолета массой m2= 200г прижимается к стволу пружиной, упругость которой k=25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.
128. Шар массой m1= 5 кг движется со скоростьюυ1 = 1 м/с и сталкивается с покоящимся шаром массойm2= 2 кг. Определить скорости u1и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
129. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью υ1= 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью υ2= 580 м/с. С какой скоростью откатилось при этом орудие?
130. Шар массой m1= 2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массуm2 большего шара. Удар считать абсолютно упругим, прямым, центральным.
131.Определить работу растяжения двух соединенных последовательно пружин упругостями k1= 400 Н/м и k2= 250 Н/м, если первая пружина при этом растянулась на ∆l=2 см.
132. Из шахты глубиной h = 600 м поднимают клеть массой m1= 3,0 т на канате, каждый метр которого имеет массу m = 1,5 кг . Какая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия η подъемного устройства?
133. Пружина упругостью k = 500 Н/м сжата силой F= 100 Н. Определить работу А внешней силы, дополнительно сжимающей пружину еще на ∆l = 2 см.
134. Две пружины упругостями k1= 0,5 кН/м и k2= 1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации ∆l = =4 см..
135. Какую нужно совершить работу А, чтобы пружину упругостью k=800Н/м , сжатую на х = 6 см , дополнительно сжать на ∆х = 8 см.?
136. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на ∆l = 3 см. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h=8 см?
137. Из пружинного пистолета с пружиной упругостью k = 150 Н/м был произведен выстрел пулей массой m = 8 г. Определить скорость υ пули при вылете ее из пистолета, если пружина была сжата на ∆х = 4 см.
138. Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью υ = 0,6 м/с, остановился, сжав пружину на ∆l = 8 см. Найти общую упругость k пружин буфера.
139. Цепь длиной l = 2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает ⅓l, то цепь соскальзывает со стола. Определить скорость υ цепи в момент отрыва ее от стола.
140. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h = 40 м , наружным диаметром D=3,0 м и внутренним диаметром d = 2,0м? Плотность материала ρ принять равной 2,8∙103кг/м3.
Контрольная работа 2
201. Определить количество вещества ν и число N молекул кислорода массой m = 0,6 кг.
202. Сколько атомов содержится в ртути: 1) количеством вещества ν=0,2 моль; 2) массой m=3 г?
203. Вода при температуре t = 4оС занимает объем V= 1 см 3. Определить количество вещества ν и число N молекул воды.
204. Найти молярную массу М массу m одной молекулы поваренной соли.
205. Определить массу mм одной молекулы углекислого газа.
206. Определить концентрацию n молекул кислорода, находящегося в сосуде вместимостью V= 2 л. Количество вещества ν кислорода равно 0,2 моль.
207. Определить количество вещества ν водорода, заполняющего сосуд объемом V= 5 л, если концентрация молекул газа в сосуде n = 4 ∙10 18м -3.
208. В баллоне вместимостью V= 6 л содержится кислород массой m= 40 г. Определить концентрацию n молекул газа.
209. Определить относительную молекулярную массу Мr: 1) воды; 2) углекислого газа; 3) поваренной соли.
210. Определить количество вещества ν и число N молекул азота массой m=0,2 кг.
211. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию молекулы этого газа при температуре Т=360 К, если количество вещества ν этого газа равно 0,6 моль.
212. Определить суммарную кинетическую энергию Ек поступательного движения всех молекул газа, находящегося в сосуде вместимостью V= 4 л под давлением р = 540 кПа.
213. Количество вещества гелия ν =1,5моль, температура Т=120 К. Определить суммарную кинетическую энергию Ек поступательного движения всех молекул этого газа.
214. Молярная внутренняя энергия Um некоторого двухатомного газа равна 6,02 кДж/моль. Определить среднюю кинетическую энергию вращательного движения одной молекулы этого газа. Газ считать идеальным.
215. Определить среднюю кинетическую энергию одной молекулы водяного пара при температуре Т= 600 К.
216. Определить среднюю квадратичную скорость молекулы газа, заключенного в сосуд вместимостью V= 2л под давлением р = 200 кПа. Масса газа m = 0,3 г.
217. Водород находится при температуре Т =300 К. Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также суммарную кинетическую энергию Ек всех молекул этого газа; количество водорода ν =0,5моль.
218. При какой температуре средняя кинетическая энергия поступательного движения молекулы газа равна 4,14∙10 - 21 Дж?
209. Определить относительную молекулярную массу Мr: 1) воды; 2) углекислого газа; 3) поваренной соли.
210. Определить количество вещества ν и число N молекул азота массой m = 0,2 кг.
211. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию молекулы этого газа при температуре Т=360 К, если количество вещества ν этого газа равно 0,6 моль.
212. Определить суммарную кинетическую энергию Ек поступательного движения всех молекул газа, находящегося в сосуде вместимостью V= 4 л под давлением р = 540 кПа.
213. Количество вещества гелия ν =1,5моль, температура Т=120 К. Определить суммарную кинетическую энергию Ек поступательного движения всех молекул этого газа.
214. Молярная внутренняя энергия Um некоторого двухатомного газа равна 6,02 кДж/моль. Определить среднюю кинетическую энергию вращательного движения одной молекулы этого газа. Газ считать идеальным.
215. Определить среднюю кинетическую энергию одной молекулы водяного пара при температуре Т = 600 К.
216. Определить среднюю квадратичную скорость молекулы газа, заключенного в сосуд вместимостью V= 2л под давлением р = 200 кПа. Масса газа m = 0,3 г.
217. Водород находится при температуре Т = 300 К. Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также суммарную кинетическую энергию Ек всех молекул этого газа; количество водорода ν =0,5моль.
218. При какой температуре средняя кинетическая энергия поступательного движения молекулы газа равна 4,14∙10 - 21 Дж?
219. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса каждой пылинки равна 6∙10-10г. Газ находится при температуре Т= 400 К. Определить средние квадратичные скорости, также средние кинетические энергии поступательного движения молекулы азота и пылинки.
220. Определить среднюю кинетическую энергию поступательного движения и вращательного движения молекулы азота при температуре Т = 1 К. Определить также полную кинетическую энергию Ек молекулы при тех же условиях.
221. Определить молярную массу М двухатомного газа и его удельные теплоемкости, если известно, что разность ср- сV удельных теплоемкостей этого газа равна 260 Дж/(кг∙К).
222. Найти удельные ср и сV, а также молярные Ср и СV теплоемкости углекислого газа.
223. Определить показатель адиабаты γ идеального газа, который при температуре Т =350 К и давлении р = 0,4 МПа занимает объем V= 300 л и имеет теплоемкость СV= 857 Дж/К.
224. В сосуде вместимостью V= 6 л находится при нормальных условиях двухатомный газ. Определить теплоемкость СV этого газа при постоянном объеме.
225. Определить относительную молекулярную массу Мr и молярную массу М газа , если разность его удельных теплоемкостей ср- сV =2,08 кДж/(кг∙К).
226. Определить молярные теплоемкости газа, если его удельные теплоемкости сV= 10,4 кДж/(кг∙К) и ср= 14,6 кДж/(кг∙К).
227. Найти удельные ср и сV и молярные Ср и СV теплоемкости азота и гелия.
228. Вычислить удельные теплоемкости газа, зная, что его молярная масса М = 4 ∙10 - 3 кг/моль и отношение теплоемкостей Ср/ СV= 1,67.
229. Трехатомный газ под давлением р= 240 кПа и температуре t = 20 оС занимает объем V= 10 л . Определить теплоемкость Ср этого газа при постоянном давлении.
230. Одноатомный газ при нормальных условиях занимает объем V=5л. Вычислить теплоемкость СV этого газа при постоянном объеме.
231. Определить количество теплоты Q, которое надо сообщить кислороду объемом V= 50 л при его изохорном нагревании, чтобы давление газа повысилось на ∆р = 0,5 МПа.
232. При изотермическом расширении азота при температуре Т=280К объем его увеличился в три раза. Определить: 1) совершенную при расширении газа работу А; 2) изменение ∆U внутренней энергии; 3) количество теплоты Q, полученное газом. Масса азота m= 0,3 кг.
233. При адиабатном сжатии давление воздуха было увеличено от р1= 50 кПа до р2= 0,5 МПа. Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление р3газа в конце процесса.
234. Кислород массой m=200 г занимает объем V1= 100 л и находится под давлением р1= 200 кПа . При нагревании газ расширился при постоянном давлении до объема V2= 300 л, а затем его давление возросло до р3= 500 кПа при неизменном объеме. Найти изменение внутренней энергии ∆U газа, совершенную газом работу А и теплоту Q, переданную газу. Построить график процесса.
235. Объем водорода при изотермическом расширении при температуре Т =300 К увеличился в n = 5 раз. Определить работу А, совершенную газом и теплоту Q, полученную при этом. Масса m водорода равна 200 г.
236. Азот массой m=0,2 кг был изобарно нагрет от температуры Т1=200 К до температуры Т2=500 К. Определить работу А, совершенную газом, полученную им теплоту Q и изменение ∆U внутренней энергии азота.
237. Во сколько раз увеличится объем водорода, содержащий количество вещества ν =0,4 моль при изотермическом расширении, если при этом газ получит количество теплоты Q= 800 Дж? Температура водорода Т=300 К.
238. Какая работа А совершается при изотермическом расширении водорода массой m=10 г, взятого при температуреТ=290 К, если объем газа увеличивается в три раза?
239. Какая доля ω1количества теплоты Q, подводимого к идеальному двухатомному газу при изобарном процессе, расходуется на увеличение ∆U внутренней энергии газа и какая доляω2 –на работу А расширения? Рассмотреть три случая, если газ 1) одноатомный; 2) двухатомный; 3) трехатомный.
240. Определить работу А, которую совершит азот, если ему при постоянном давлении сообщить количество теплоты Q=21кДж. Найти также изменение ∆U внутренней энергии газа.
241. Идеальный газ совершает цикл Карно при температурах теплоприемникаТ2=290 К и теплоотдатчика Т1= 400 К. Во сколько раз увеличится коэффициент полезного действия η цикла, если температура теплоотдатчика возрастает до Т1'= 600 К ?
242. Идеальный газ совершает цикл Карно. Температура Т1 теплоотдатчика в четыре раза (n=4) больше температуры теплоприемника. Какую долю ω количества теплоты, полученного за один цикл от теплоотдатчика, газ отдаст теплоприемнику?
243. Определить работу А2 изотермического сжатия газа, совершающего цикл Карно, к.п.д. которого η = 0,4,если работа изотермического расширения равна А1= 8Дж.
244. Газ, совершающий цикл Карно, отдал теплоприемнику теплоту Q2 = 14 кДж. Определить температуру Т1теплоотдатчика, если при температуре теплоприемника Т2=280 К работа цикла А = 6кДж.
245. Газ, являясь рабочим веществом в цикле Карно, получил от теплоотдатчика Q1= 4,38 кДж и совершил работу А= 2,4 кДж. Определить температуру теплоотдатчика, если температура теплоприемника Т2 =273 К.
246. Газ, совершающий цикл Карно, отдал теплоприемнику 67% теплоты, полученной от теплоотдатчика. Определить температуру Т2 теплоприемника, если температура теплоотдатчика Т1= 430 К.
247. Во сколько раз увеличится коэффициент полезного действия η цикла Карно при повышении температуры теплоотдатчика от Т1= 380 К до Т1'=560 К? Температура теплоприемника Т2 =280 К.
248. Идеальная тепловая машина работает по циклу Карно. Температура теплоотдатчика Т1=500 К, температура теплоприемника Т2 =250 К.Определить термический к.п.д. η цикла, а также работу А1 рабочего вещества при изотермическом расширении, если при изотермическом сжатии совершена работа А2=70 Дж.
249. Газ, совершающий цикл Карно, получает теплоту Q1= 84 кДж. Определить работу А газа, если температура Т1 теплоотдатчика в три раза выше температуры Т2теплоприемника.
250. В цикле Карно газ получил от теплоотдатчика теплоту Q1=500 Дж и совершил работу А=100Дж. Температура теплоотдатчика Т1 = 400 К.Определить температуру Т2 теплоприемника.
251. Точечные заряды Q1 = 10 мкКл, Q2 = - 20 мкКл находятся на расстоянии d = 5 см друг от друга. Определить напряженность поля в точке, удаленной на r1= 3 см от первого и на r2= 4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд Q= 1 мкКл.
252. Три одинаковых точечных заряда Q1= Q2= Q3 = 3 нКл находятся в вершинах равностороннего треугольника со сторонами а = 10 см. Определить модуль и направление силы 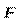 , действующей на один из зарядов со стороны двух других.
, действующей на один из зарядов со стороны двух других.
253. Два положительных точечных заряда Q и 9Q закреплены на расстоянии d = 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
254. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α . Шарики погружают в масло. Какова плотность ρ масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков ρо= 1,5∙10 3кг/м3,диэлектрическая проницаемость масла ε = 2,2.
255. Четыре одинаковых заряда Q1= Q2= Q3 = Q4= 40 нКл закреплены в вершинах квадрата со стороной а = 10 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.
256. Точечные заряды Q1 = 10 мкКл и Q2 = - 20 мкКл находятся на расстоянии d = 20 см друг от друга. Определить напряженность электрического поля 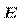 в точке, удаленной от первого заряда на расстояние r1= 30 см, а от второго - на r2= 15 см .
в точке, удаленной от первого заряда на расстояние r1= 30 см, а от второго - на r2= 15 см .
257. В вершинах правильного треугольника со стороной а = 10 см находятся заряды Q1 = 10 мкКл, Q2 = 20 мкКл и Q3= 30 мкКл . Определить силу 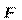 ,действующую на заряд Q1со стороны двух других зарядов.
,действующую на заряд Q1со стороны двух других зарядов.
258. В вершинах квадрата находятся одинаковые заряды Q1= Q2= Q3 = Q4 = 8∙10 – 10 Кл. Какой отрицательный заряд Q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?
259. На расстоянии d = 20 см находятся два точечных заряда.: Q1 = - 50 нКл и Q2 = 100 нКл. Определить силу 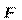 , действующую на заряд Q3= -10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
, действующую на заряд Q3= -10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
260. Расстояние d между двумя точечными зарядами Q1 = 2 нКл и Q2 = 4 нКл равно 60 см. Определить точку, в которую нужно поместить третий заряд Q3так, чтобы система зарядов находилась в равновесии. Определить заряд Q3и его знак. Устойчивое или неустойчивое будет равновесие?
261. Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд τ =0,1 мкКл. Определить напряженность 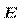 электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его конца.
электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его конца.
262. Две параллельные заряженные плоскости, поверхностные плотности заряда которых σ1= 2 мкКл/м2и σ2 = - 0,8мкКл/м2,находятся на расстоянии d = 0,6 см друг от друга. Определить разность потенциалов U между плоскостями.
263. Электрон, обладавший кинетической энергией Т = 10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U = 8 В?
264. Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом φ1 = 100 В электрон имел скорость υ1= 6 Мм/с. Определить потенциал φ2точки поля, дойдя до которой электрон потеряет половину своей скорости.
265. Пылинка массой m = 200 мкг, несущая на себе заряд Q=40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U= 200 В пылинка имела скорость υ = 10 м/с.Определить скорость υо пылинки до того, как она влетела в поле.
266. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость υ = 105 м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разности потенциалов U между пластинами; 2) поверхностную плотность заряда σ на пластинах.
267. Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой τ = 20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r1 = 8 см и r2 = 12 см 268. Электрон с энергией Т = 400 эВ (в бесконечности)движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное расстояние а на которое приблизится электрон к поверхности сферы, если заряд ее Q= - 10 нКл.
269. Конденсаторы емкостью С1= 5 мкФ и С2= 10 мкФ заряжены до напряжений U1= 60 В и U2=100В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.
270. Конденсатор емкостью С1= 10 мкФ заряжен до напряжения U= 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор емкостью С2= 20 мкФ.
271. Конденсаторы емкостямиС1= 2 мкФ, С2= 5 мкФ и С3= 10 мкФ соединены последовательно и находятся под напряжением U= 850 В. Определить напряжение и заряд на каждом из конденсаторов.
272. Два конденсатора емкостями С1=2 мкФ и С2= 5 мкФ заряжены до напряжений U1= 100 В и U2=150В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.
273. Два одинаковых плоских воздушных конденсатора емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.
274. Два конденсатора емкостями С1 = 5 мкФ и С2 = 8 мкФ соединены последовательно и присоединены к батарее с ЭДС ε=80 В. Определить заряды Q1 и Q2 конденсаторов и разности потенциаловU1 и U2 между их обкладками.
275. Плоский конденсатор состоит из двух круглых пластин радиусом R= 10 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор присоединен к источнику напряжения U= 80 В. Определить заряд Q и напряженность Е поля конденсатора в двух случаях: а) диэлектрик – воздух; б) диэлектрик– стекло.
276. Два металлических радиусами R1= 5 см и R2 = 10 см имеют заряды Q1= 40 нКл и Q2= - 20 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводником.
277. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стекла толщиной d1 = 0,2 см и слоем парафина толщиной d2 = 0,3 см. Разность потенциалов между обкладками U= 300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.
278. Плоский конденсатор с площадью пластин S= 200 см 2 каждая заряжен до разности потенциалов U= 2 кВ. Расстояние между пластинами d = 2 см. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность энергии w поля.
.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНБАССКАЯ АГРАРНАЯ АКАДЕМИЯ»
Дата: 2018-11-18, просмотров: 731.
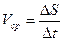
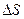 - путь, пройденный материальной точкой за все время движения
- путь, пройденный материальной точкой за все время движения 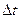 .
.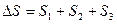
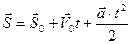
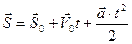 (1)
(1)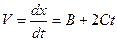
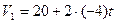 ;
; 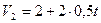 .
.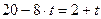 . (1)
. (1)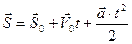 (1)
(1) 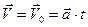 (2)
(2)