1. Найти пределы функций:
а) 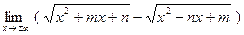 ;
;
б) 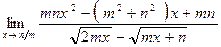 ;
;
в) 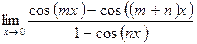 ;
;
г) 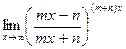 .
.
2. В точках 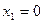 и
и 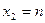 для функции
для функции 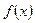 установить непрерывность или определить характер точек разрыва. Нарисовать график функции
установить непрерывность или определить характер точек разрыва. Нарисовать график функции 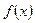 в окрестностях этих точек:
в окрестностях этих точек:
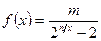 ;
;
Производные функций.
3. Найти производные 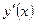 функций:
функций:
а) 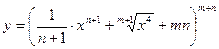 ; б)
; б) 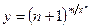 ;
;
в) 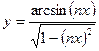 ; д)
; д) 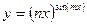 ; е)
; е) 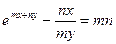 ;
;
ж) 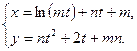
A. Приложения производной.
С помощью методов дифференциального исчисления построить графики функций:
а) 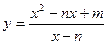 ; б)
; б) 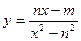
Найти наибольшее и наименьшее значение функции 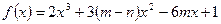 на отрезке
на отрезке 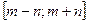
B. Приближенное решение алгебраических уравнений.
Для уравнения 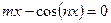 отделить положительный корень и найти его приближенно с точностью
отделить положительный корень и найти его приближенно с точностью 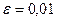 :
:
а) методом деления отрезка пополам;
б) методом касательных.
Примечание. Можно считать, что точность 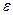 достигнута, если разность между соседними приближениями
достигнута, если разность между соседними приближениями 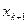 и
и 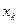 удовлетворяет неравенству
удовлетворяет неравенству 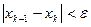 .
.
Интегральное исчисление
Неопределенный интеграл.
1. Найти интегралы:
а) 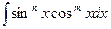 б)
б) 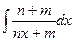
в) 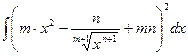 г)
г) 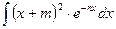 ;
;
д) 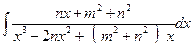 ; е)
; е) 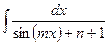 .
.
Несобственные интегралы.
2. Вычислить интеграл или установить его расходимость:
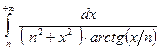
A. Применения определенных интегралов.
Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
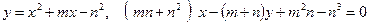 ;
;
Найти объем тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями:
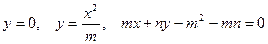 .
.
B. Приближенное вычисление определенных интегралов.
Для вычисления определенного интеграла 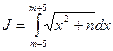 , разбивая отрезок интегрирования сначала на 10 равных частей, а затем на 20 равных частей, найти приближенное значение
, разбивая отрезок интегрирования сначала на 10 равных частей, а затем на 20 равных частей, найти приближенное значение 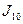 и
и 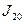 : а) по формуле трапеций; б) по формуле Симпсона. Оценить точность приближения с помощью разности
: а) по формуле трапеций; б) по формуле Симпсона. Оценить точность приближения с помощью разности 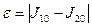 .
.
Краткое содержание (программа) курса
Линейная алгебра.
Матрицы, действия над ними. Определители, их свойства и вычисление. Обратная матрица. Системы линейных уравнений, условие их совместности. Формулы Крамера, метод Гаусса и матричный способ решения систем. Линейный оператор. Собственные векторы и собственные значения линейных операторов.
Аналитическая геометрия.
Простейшие задачи аналитической геометрии (расстояние между точками, деление отрезка в заданном отношении). Прямая на плоскости, различные виды ее уравнений, угол между прямыми. Расстояние от точки до прямой. Геометрический смысл линейных уравнений и неравенств. Кривые второго порядка, их канонические уравнения.
Векторы, линейные операции над ними. Координаты вектора, его длина, направляющие косинусы. Скалярное, векторное и смешанное произведения векторов, условия их перпендикулярности, коллинеарности, компланарности.
Плоскость в пространстве, ее уравнения, угол между плоскостями, расстояние от точки до плоскости. Прямая в пространстве, ее общие и канонические уравнения. Угол между прямой и плоскостью.
Дата: 2018-11-18, просмотров: 643.