МАТЕМАТИКА
ПРАКТИКУМ по выполнению
контрольных работ для студентов всех специальностей
Практикум содержит задачи для контрольных работ по всем курсам математических дисциплин, предусмотренным учебными планами специальностей, и краткий перечень вопросов для подготовки к экзаменам.
Каждая контрольная работа состоит из задач одного или нескольких разделов данного сборника, выбранных в соответствии с рабочей программой.
Перечень разделов сборника, необходимых для выполнения контрольных работ по каждой специальности, сообщается студентам этой специальности в начале семестра.
ФОРМИРОВАНИЕ ИСХОДНЫХ ДАННЫХ К ЗАДАЧАМ
Каждая контрольная работа состоит из задач одного или нескольких разделов сборника.
Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.
Числовых данных параметров т и п определяются по двум последним цифрам своего шифра зачетки (А — предпоследняя цифра, В — последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п - из таблицы 2. Эти два числа т и п и нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
| А | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| т | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
Таблица 2 (выбор параметра п )
| В | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| п | 3 | 5 | 4 | 2 | 1 | 5 | 4 | 1 | 3 | 2 |
Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что т =4, п =1. Полученные т = 4 и п = 1 подставляются в условия всех задач контрольной работы этого студента.
Дифференциальное исчисление
Пределы, непрерывность и разрывы функций.
1. Найти пределы функций:
а) 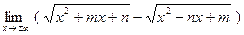 ;
;
б) 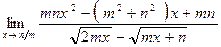 ;
;
в) 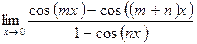 ;
;
г) 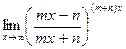 .
.
2. В точках 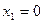 и
и 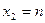 для функции
для функции 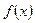 установить непрерывность или определить характер точек разрыва. Нарисовать график функции
установить непрерывность или определить характер точек разрыва. Нарисовать график функции 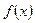 в окрестностях этих точек:
в окрестностях этих точек:
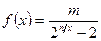 ;
;
Производные функций.
3. Найти производные 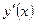 функций:
функций:
а) 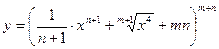 ; б)
; б) 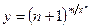 ;
;
в) 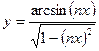 ; д)
; д) 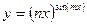 ; е)
; е) 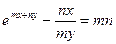 ;
;
ж) 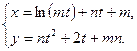
A. Приложения производной.
С помощью методов дифференциального исчисления построить графики функций:
а) 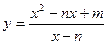 ; б)
; б) 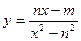
Найти наибольшее и наименьшее значение функции 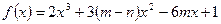 на отрезке
на отрезке 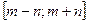
B. Приближенное решение алгебраических уравнений.
Для уравнения 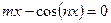 отделить положительный корень и найти его приближенно с точностью
отделить положительный корень и найти его приближенно с точностью 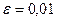 :
:
а) методом деления отрезка пополам;
б) методом касательных.
Примечание. Можно считать, что точность 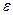 достигнута, если разность между соседними приближениями
достигнута, если разность между соседними приближениями 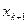 и
и 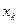 удовлетворяет неравенству
удовлетворяет неравенству 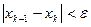 .
.
Интегральное исчисление
Неопределенный интеграл.
1. Найти интегралы:
а) 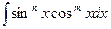 б)
б) 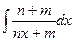
в) 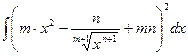 г)
г) 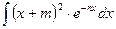 ;
;
д) 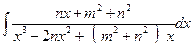 ; е)
; е) 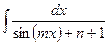 .
.
Несобственные интегралы.
2. Вычислить интеграл или установить его расходимость:
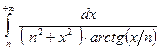
Линейная алгебра.
Матрицы, действия над ними. Определители, их свойства и вычисление. Обратная матрица. Системы линейных уравнений, условие их совместности. Формулы Крамера, метод Гаусса и матричный способ решения систем. Линейный оператор. Собственные векторы и собственные значения линейных операторов.
Аналитическая геометрия.
Простейшие задачи аналитической геометрии (расстояние между точками, деление отрезка в заданном отношении). Прямая на плоскости, различные виды ее уравнений, угол между прямыми. Расстояние от точки до прямой. Геометрический смысл линейных уравнений и неравенств. Кривые второго порядка, их канонические уравнения.
Векторы, линейные операции над ними. Координаты вектора, его длина, направляющие косинусы. Скалярное, векторное и смешанное произведения векторов, условия их перпендикулярности, коллинеарности, компланарности.
Плоскость в пространстве, ее уравнения, угол между плоскостями, расстояние от точки до плоскости. Прямая в пространстве, ее общие и канонические уравнения. Угол между прямой и плоскостью.
Интегральное исчисление.
Неопределенный интеграл, его основные свойства. Таблица интегралов. Интегрирование подстановкой и по частям. Интегрирование дробно-рациональных, тригонометрических и иррациональных функций.
Интегральная сумма. Определенный интеграл, его геометрический смысл. Свойства определенного интеграла. Формула Ньютона-Лейбница. Интегрирование по частям и замена переменной в определенном интеграле. Несобственные интегралы. Приложения определенного интеграла.
Использование понятия определенного интеграла в экономике.
Элементы теории поля.
Поверхностные интегралы. Поток векторное поля через ориентированную поверхность, его физический смысл. Дивергенция векторного поля, свойства. Теорема Остроградского. Линейный интеграл. Циркуляция векторного поля. Ротор (вихрь) векторного поля, свойства ротора. Теорема Стокса. Потенциальное поле. Потенциал. Соленоидальное поле.
Ряды.
Числовые ряды, сходимость и сумма ряда. Необходимое условие сходимости. Свойства сходящихся рядов. Достаточные признаки сходимости рядов с неотрицательными членами (признаки сравнения, Даламбера, Гаусса, радикальный признак Коши, интегральный признак). Знакочередующиеся ряды. Признак Лейбница. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды. Функциональные ряды, область сходимости, методы её определения.Степенные ряды, действия над ними. Теорема Абеля о сходимости степенных рядов. Формулы для вычисления радиуса сходимости степенных рядов. Ряды Тейлора и Маклорена. Разложение функций у =sin x, cos x, ex, (1+x)m, ln (1+x), arctg x в степенные ряды. Применение степенных рядов в приближенных вычислениях (приближенное вычисление значений функций, определенных интегралов, приближенное решение дифференциальных уравнений). Тригонометрические ряды Фурье. Разложение функций в тригонометрические ряды Фурье.
Операционное исчисление.
Начальная функция (оригинал) и ее изображение. Теорема о существовании изображения. Теорема единственности оригинала. Свойство линейности изображения. Таблица оригиналов и изображений изображений некоторых функций. Теорема подобия. Теорема смещения. Теорема запаздывания. Теорема свертывания. Дифференцирование оригиналов. Интегрирование оригиналов. Таблица оригиналов и их изображений. Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами.
Теория вероятностей.
Случайные события, алгебра событий. Относительная частота, статистическое определение вероятности. Классическое определение вероятности. Геометрическое определение вероятности, задача о встрече. Формулы комбинаторики. Теоремы сложения. Независимые события, теоремы умножения. Формула полной вероятности. Формулы Байеса. Повторение испытаний. Формула Бернулли. Наивероятнейшее число событий. Локальная и интегральная теоремы Лапласа. Случайные величины. Функция распределения (интегральный закон распределения). Плотность распределения (дифференциальный закон распределения). Математическое ожидание, его свойства. Дисперсия, ее свойства, среднее квадратическое отклонение. Основные примеры распределений случайных величин (биномиальное, геометрическое, гипергеометрическое, Пуассона, равномерное, показательное, нормальное). Вероятность попадания в заданный интервал нормально распределенной случайной величины Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс. Распределения, связанные с нормальным. Многомерные случайные величины. Числовые характеристики системы случайных величин. Коэффициент корреляции. Законы больших чисел. Предельные теоремы.
Математическая статистика.
Выборочный метод, статистическое распределение. Эмпирическая функция распределения. Полигон и гистограмма. Оценка параметров, свойства точечных оценок. Условные варианты, метод произведений. Доверительный интервал. Метод наибольшего правдоподобия. Статистическая проверка статистических гипотез. Критерии согласия. Метод наименьших квадратов. Уравнение прямой линии регрессии. Выборочный коэффициент корреляции.
Линейное программирование.
Общая и основная задачи линейного программирования (ЛП). Основные теоремы ЛП. Геометрический метод решения задач ЛП. Симплек-метод: определение первоначального допустимого базисного решения; проверка решения на оптимальность; переход к другому допустимому решению. Двойственные задачи: их свойства; теоремы двойственности; объективно обусловленные оценки и их смысл. Транспортная задача: экономико-математическая модель транспортной задачи; нахождение первоначального базисного распределения поставок (метод «северо-западного» угла, метод наименьших затрат); критерий оптимальности базисного распределения поставок; перераспределение поставок; вырождение транспортной задачи; открытая модель транспортной задачи. Элементы теории игр: основные понятия; антагонистические игры, платежная матрица; решение игр в смешанных стратегиях; геометрические решения игр размера 2xn, mx2; приведение матричной игры к задаче ЛП.
Дискретная математика.
Высказывания, логические операции над ними. Равносильность формул логики высказываний. Алгебра Буля. Представление булевой функции формулой логики высказываний. Закон двойственности. Нормальные и совершенные нормальные формы формул. Предикаты, логические операции над ними. Кванторные операции. Формулы логики предикатов, их равносильность, нормальная форма. Комбинаторные схемы. Основные понятия и определения теории графов. Изоморфизм. Матричное задание графов. Операции над графами. Кратчайший путь между вершинами. Алгоритм Дейкстры. Поток в транспортной сети. Теорема Форда-Фалкерсона. Задача о максимальном потоке. Алгоритм Форда-Фалкерсона.
Список учебной литературы
1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
2. Алдохин И.П. Теория массового обслуживания в промышленности. – М.: Экономика,1980.
3. Бугров Я.С., Никольский С.М. Высшая математика, в трёх томах. – М: Дрофа, 2003.
4. Вентцель Е.С. Прикладные задачи теории вероятностей. – М.:Наука,1984.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2003.
6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2006.
7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Том 1,2. – М.: Высшая школа, 2000.
8. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1980.
9. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974.
10. Краснов М.Л., Киселев А.И., Макаренко Г.Н. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. – М.: Наука, 1981.
11. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2007
12. Кремер Н.Ш. Исследование операций в экономике. М.: Юнити, 2007
13. Кузнецов Ю.Н., Кузубов В.И., Велощенко А.Б. Математическое программирование. – М.: Высшая школа, 1980.
14. Ларионов А.И., Юрченко Т.И., Новоселов А.Л. Экономико—математические методы. – М.: Высшая школа, 1991.
15. Пискунов Н.С. Дифференциальное и интегральное исчисления Том 1,2.— М.: Наука, 1988.
16. Письменный Д. Г. Конспект лекций по высшей математике. Части I и II. – М: «Айрис Пресс» 2004 г.
17. Романовский. П.Н. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. – М.: Наука, 1986.
18. Свешников А.Г., Тихонов А.Н. Теория функций комплексного переменного. – М.: Наука, 1984.
19. Сидорович А.В. Математические методы в экономике. – М.: Дело и сервис, 2001
20. Терехов Л.Л. Экономико—математические методы.—М.: Статистика, 1982.
Никитин Сергей Ильич
Кропачева Наталия Юрьевна
Бритаева Ольга Хаджи-Муратовна
Хабурзания Манана Георгиевна
МАТЕМАТИКА
ПРАКТИКУМ по выполнению контрольных работ для студентов всех специальностей
| Подп. к печати 11.06.2008 г. | Формат 60´84 1/16 | |
| Усл. печ. л. 0,86 | Уч.-изд. л. 2,0 | Тираж 1500 экз. |
| Изд. № 001 | Заказ № 029 |
РИО СПбГУСЭ, лицензия ЛР № 040849
Член Издательско-полиграфической ассоциации университетов России
Государственный регистрационный номер 2047806003595 от 06.02.2004 г.
СПб государственный университет сервиса и экономики
192171, г. Санкт-Петербург, ул. Седова, 55/1
Отпечатано в ЦОП ООО «Альфа»,
196084, г. Санкт-Петербург, ул. Заставская, 33, лит. ТА
МАТЕМАТИКА
ПРАКТИКУМ по выполнению
контрольных работ для студентов всех специальностей
Практикум содержит задачи для контрольных работ по всем курсам математических дисциплин, предусмотренным учебными планами специальностей, и краткий перечень вопросов для подготовки к экзаменам.
Каждая контрольная работа состоит из задач одного или нескольких разделов данного сборника, выбранных в соответствии с рабочей программой.
Перечень разделов сборника, необходимых для выполнения контрольных работ по каждой специальности, сообщается студентам этой специальности в начале семестра.
ФОРМИРОВАНИЕ ИСХОДНЫХ ДАННЫХ К ЗАДАЧАМ
Каждая контрольная работа состоит из задач одного или нескольких разделов сборника.
Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.
Числовых данных параметров т и п определяются по двум последним цифрам своего шифра зачетки (А — предпоследняя цифра, В — последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п - из таблицы 2. Эти два числа т и п и нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
| А | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| т | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
Таблица 2 (выбор параметра п )
| В | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| п | 3 | 5 | 4 | 2 | 1 | 5 | 4 | 1 | 3 | 2 |
Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что т =4, п =1. Полученные т = 4 и п = 1 подставляются в условия всех задач контрольной работы этого студента.
Дифференциальное исчисление
Дата: 2018-11-18, просмотров: 674.