Подставим в уравнение (5) значение входящих в него сил. Силу сопротивления воздуха на прицеп учитываем увеличенным значением коэффициента сопротивления воздуха
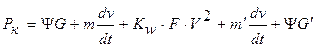
После простейших преобразований:
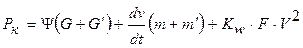 (7)
(7)
Полученное выражение является уравнением динамики в развернутом виде.
Если автомобиль одиночный, т.е. 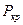 = 0, тогда
= 0, тогда
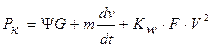
Первое уравнение динамики показывает, какая сила тяги на ведущих колесах должна развиваться, чтобы преодолеть внешние силы сопротивления движению.
В первом уравнении динамики имеется два неизвестных:
сила тяги на ведущих колесах «Рк» и ускорение ( 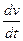 ).
).
Для решения уравнения необходимо составить второе уравнение, которым и будет ТОрое уравнение динамики или уравнение мощностей.
3.2. Второе уравнение динамики – уравнение мощностей.
М.У.: Вывод второго уравнения динамики в полном объеме не давать. Записать только начальную и конечную формулу , с целью более детального анализа конечной формулы.
Вывод второго уравнения динамики основан на теореме о кинетической энергии: изменение мощности движущегося тела равно мощности, затраченной на преодоление сил сопротивления, действующих на пути движения.
Таким образом, в случае ускоренного движения можно записать:

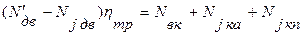
где 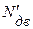 - мощность двигателя за вычетом потерь на привод вспомогательных агрегатов;
- мощность двигателя за вычетом потерь на привод вспомогательных агрегатов;
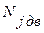 - мощность, затрачиваемая на ускорение вращения деталей двигателя, коленчатого вала, маховика с кожухом сцепления и т.д.;
- мощность, затрачиваемая на ускорение вращения деталей двигателя, коленчатого вала, маховика с кожухом сцепления и т.д.;
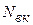 - мощность на ведущих колесах, расходуемая на преодоление внешних сопротивлений;
- мощность на ведущих колесах, расходуемая на преодоление внешних сопротивлений;
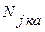 - мощность, затрачиваемая на ускорение вращения колес автомобиля и непосредственно связанных с ними деталей (полуосей, полуосевых шестерен);
- мощность, затрачиваемая на ускорение вращения колес автомобиля и непосредственно связанных с ними деталей (полуосей, полуосевых шестерен);
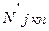 - мощность, затрачиваемая на ускорение вращения колес прицепа.
- мощность, затрачиваемая на ускорение вращения колес прицепа.
Выразим значения мощности, затрачиваемой на преодоление внешних сопротивлений NВК через первое уравнение динамики, а мощностей, затрачиваемых на раскрутку вращающихся деталей автомобиля и прицепа через моменты их инерции.
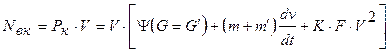 (8)
(8)
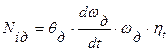 (9)
(9)
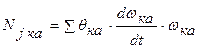 (10)
(10)
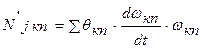 (11)
(11)
где 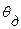 - момент инерции вращающихся деталей двигателя, приведенной к маховику;
- момент инерции вращающихся деталей двигателя, приведенной к маховику;
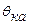 - момент инерции колес автомобиля;
- момент инерции колес автомобиля;
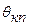 - момент инерции колес прицепа;
- момент инерции колес прицепа;
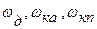 - угловые скорости соответственно двигателя, колес автомобиля и колес прицепа.
- угловые скорости соответственно двигателя, колес автомобиля и колес прицепа.
Выразив значения угловых скоростей через скорость движения автомобиля ( 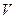 ) и подставим эти значения в выражения (9), (10), (11) получим:
) и подставим эти значения в выражения (9), (10), (11) получим:
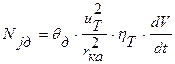 (12)
(12)
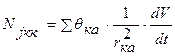 (13)
(13)
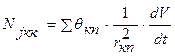 (14)
(14)
где 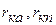 - радиусы колеса соответственно автомобиля и прицепа;
- радиусы колеса соответственно автомобиля и прицепа;
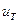 - передаточное число трансмиссии;
- передаточное число трансмиссии;
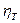 - к.п.д. трансмиссии.
- к.п.д. трансмиссии.
Подставим значения выражений (8), (12), (13), и (14) в выражение (7), и после преобразования получим:
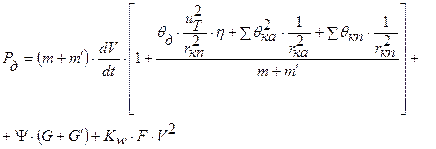 (15)
(15)
где 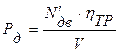 - сила тяги по двигателю
- сила тяги по двигателю
Указанное уравнение называют вторым уравнением динамики (уравнением мощности) в развернутом виде:
Выражение, взятое в скобках, в уравнении (15) часто для сокращения записи заменяют символом 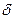 и называют коэффициентом учета вращающихся масс, т.е.
и называют коэффициентом учета вращающихся масс, т.е.
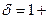
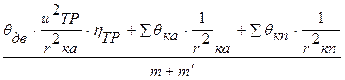 (16)
(16)
Тогда уравнение мощности примет вид:
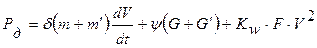 (17)
(17)
Это уравнение в литературе принято называть уравнением тягового баланса, которое показывает расход мощности двигателя на движение автопоезда с дополнительными затратами на разгон автопоезда.
Смысл безразмерного коэффициента учета вращающихся масс состоит в том, что он позволяет все слагаемые, имеющие размерность массы (показывающие меру инерционности) заменить одним слагаемым – массой машины, увеличенной в 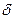 раз.
раз.
Физический смысл коэффициента учета вращающихся масс состоит в том, что в динамике (с учетом разгона или торможения) автомобиля инерционные составляющие зависят не просто от наличия тех или иных масс, разгон или замедление которых приводит к появлению дополнительных сил, а от наличия в составе автомобиля массивных быстровращающихся элементов, которые обладают способностью накапливать кинетическую энергию при разгоне, и отдавать ее при замедлении автомобиля.
Эти быстровращающиеся элементы автомобиля напоминают инерционный двигатель, представляющий собой массивный маховик, запасающий кинетическую энергию на стоянке при его раскрутке и отдающий энергию движущемуся транспортному средству.
Конечно, роль вращающихся масс на реальных автомобилях не столь значительна, как в случае использования инерционного двигателя, но в ряде случаев учет их совершенно необходим.
Так, в случае движения одиночного автомобиля доля энергии, идущая на разгон вращающихся масс относительно больше, чем в случае движения автопоезда.
Для одиночного автомобиля уравнение тягового баланса имеет вид:
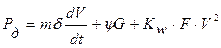 (18)
(18)
где
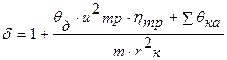 (19)
(19)
Из приведенной формулы видно, что величина коэффициента 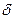 зависит от большого числа параметров, но наиболее существенный вклад обеспечивает величина общего передаточного числа трансмиссии «
зависит от большого числа параметров, но наиболее существенный вклад обеспечивает величина общего передаточного числа трансмиссии « 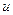 mр».
mр».
Расчет показывает, что при движении на высшей передаче величина 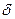 составляет 1,04 – 1,09 а при переходе на низшие передачи эта величина в некоторых случаях достигает четырех единиц.
составляет 1,04 – 1,09 а при переходе на низшие передачи эта величина в некоторых случаях достигает четырех единиц.
Это означает, что при разгонах на высших передачах доля энергии, затрачиваемой на раскрутку вращающихся деталей автомобиля относительно невелика по сравнению с долей энергии, расходуемой на увеличение скорости движения всего автомобиля.
На низших передачах, поскольку кинетическая энергия самого автомобиля сравнительно мала, а затраты на разгон вращающихся деталей практически такие же как и на высших передачах, отношение затрат мощности резко изменяется в связи с чем величина коэффициента возрастает.
Если величины моментов инерции двигателя и колес неизвестны, то для ориентировочных расчетов, а также для контроля правильности определения порядка величины 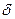 можно пользоваться эмпирической формулой:
можно пользоваться эмпирической формулой:

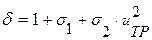
 (20)
(20)
где 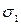 - коэффициент, учитывающий вращающиеся массы колес принимают
- коэффициент, учитывающий вращающиеся массы колес принимают 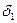 = 0,03 + 0,05
= 0,03 + 0,05
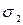 - коэффициент, учитывающий вращающиеся массы элементов трансмиссии двигателя:
- коэффициент, учитывающий вращающиеся массы элементов трансмиссии двигателя: 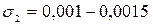
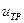 - передаточное число трансмиссии.
- передаточное число трансмиссии.
Иногда требуется определить коэффициент учета вращающихся масс при движении накатом. В этом случае в формуле расчета 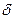 часть параметров принимают равной нулю (
часть параметров принимают равной нулю ( 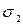 ;
; 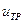 ). Тогда на величину коэффициента влияют только параметры колес. В этом случае коэффициент учета вращающихся масс принимают равным 1,05
). Тогда на величину коэффициента влияют только параметры колес. В этом случае коэффициент учета вращающихся масс принимают равным 1,05
Такого же порядка берется коэффициент для расчета инерционной силы для прицепа.
При равномерном движении изменение скорости равно нулю, а значит, инерционная сила также равна нулю.

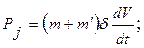 при
при 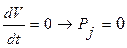
Тогда сила тяги по двигателю равна окружной силе на ведущих колесах
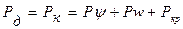
В случае замедленного движения автомобиля, вращающиеся массы двигателя и трансмиссии вследствие своей инерционности стараются поддержать высокую скорость движения, что необходимо учитывать при торможении автомобиля, преодолении препятствий с разгона и т.п.
При разгоне с точки зрения экономичности желательно переходить на высшие передачи, как только позволяют дорожные условия, т.к. доля энергии, затрачиваемая непосредственно на ускорение движения автомобиля на высших передачах выше.
М.У. Указать, что при движении на подъем целесообразно включать низшие передачи, учитывая, что движение с замедлением дает возможность использовать инерционные моменты вращающихся масс для поддержания движения без переключения передач
В случае использования на автомобиле непрерывной (но ступенчатой передачи. Например, гидромеханической, величина коэффициента учета масс может находиться несколько иначе, т.к. для непрерывной передачи происходит изменение передаточного отношения в ходе изменения скорости автомобиля.
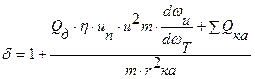
где 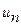 - постоянное передаточное отношение в планетарной или вальной коробке передач, соединенной с гидротрансформатором;
- постоянное передаточное отношение в планетарной или вальной коробке передач, соединенной с гидротрансформатором;
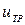 - передаточное отношение гидротрансформатора;
- передаточное отношение гидротрансформатора;
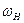 - угловая скорость ведущего вала гидротрансформатора;
- угловая скорость ведущего вала гидротрансформатора;
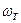 - угловая скорость ведомого вала гидротрансформатора.
- угловая скорость ведомого вала гидротрансформатора.
Производная 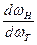 характеризует зависимость изменения угловой скорости ведущего вала гидротрансформатора от изменения угловой скорости ведомого вала (т.е. «прозрачность»).
характеризует зависимость изменения угловой скорости ведущего вала гидротрансформатора от изменения угловой скорости ведомого вала (т.е. «прозрачность»).
ЗАКЛЮЧЕНИЕ
Подвести итог занятия. Напомнить изученные на занятии учебные вопросы и их значимость для изучения последующих тем. Подчеркнуть еще раз особую значимость учебного материала, изученного на занятии для понимания других тем теории колесных машин и для практической эксплуатации автомобилей.
Дать задание на самостоятельную работу (приложение 1).
Объявить тему следующего занятия и особенности подготовки к нему.
Дата: 2018-11-18, просмотров: 638.