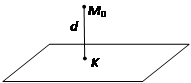
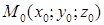Пусть требуется найти расстояние от точки  до плоскости, заданной уравнением в общем виде 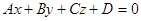. Проведем из точки  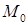перпендикуляр  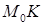на данную плоскость.

Тогда расстояние d от точки 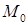 до плоскости будет равно модулю вектора 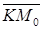, который коллинеарен нормальному вектору 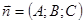. Поэтому, используя формулу скалярного произведения, получим

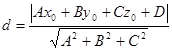                                                                 (2.4)

Пример 2.4. Найти расстояние от точки 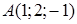 до плоскости .

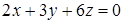Решение. Используя формулу (2.4), получим .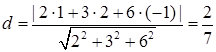

Ответ: .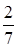

Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей

Пусть две плоскости заданы уравнением в общем виде:

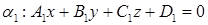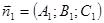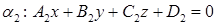, где ;

, где ;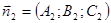

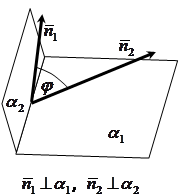
Угол между двумя плоскостями

Углом между двумя плоскостями будем называть любой из двух смежных двугранных углов. Один из них равен углу между нормальными векторам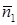и  и 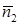 заданных плоскостей. Поэтому угол  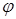между двумя плоскостями определяется следующим образом:

,

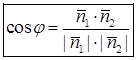или в координатной форме

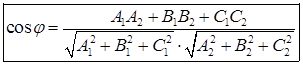                                                (3.1)

Пример 3.1  Найти угол между плоскостям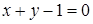и  и .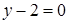

Решение. Найдем нормальные векторы плоскостей: 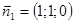, 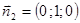. По формуле (2.1)

.

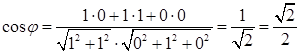Следовательно, угол j = 45°.

Условие параллельности двух плоскостей

Условие параллельности плоскосте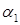й  и 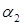 в векторной форме может быть записано в виде 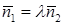, что равносильно условию

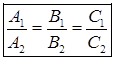,                                                               (3.2)

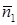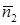где соответствующие координаты нормальных векторов  и  плоскосте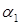й  и 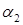 пропорциональны.

Пример 3.2 Установить, являются ли плоскост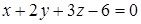и  и 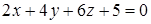 параллельными. Построить первую плоскость.

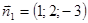Решение. а) Найдем нормальные векторы плоскостей:  и 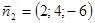. Запишем условие (3.2):  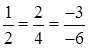– верно. Следовательно, плоскости параллельны.

б) Преобразуем уравнение плоскости 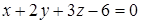 к виду 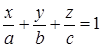. Получим .

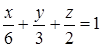Построим плоскость.

Условие перпендикулярности двух плоскостей.

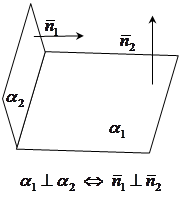Если плоскост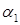и  и 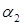 взаимно перпендикулярны, то их нормальные векторы  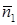и 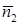 также перпендикулярны. Поэтому скалярное произведение векторов  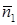и 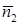 равно 0. Следовательно, условие перпендикулярности плоскосте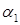й  и 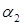 в соответственно векторной и координатной формах имеет вид

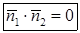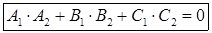,                  (3.3)

Пример 3.3 Установить, являются ли плоскост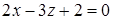и  и 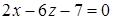 перпендикулярными?

Решение. Найдем нормальные векторы плоскосте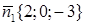й:  и 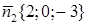. Используем формулу (3.3). Т.к. 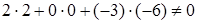, то делаем вывод, что плоскости не перпендикулярны.

Пример 3.4 Вычислить расстояние между параллельными плоскостям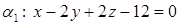и  и .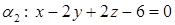

Решение. Т.к. плоскости параллельны, то все точки плоскости 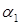 одинаково удалены от плоскости 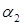. Найдем точку, лежащую на плоскости 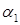. Возьмем 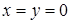, тогда из уравнения плоскости  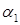получим 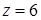. Значит, точка  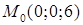лежит на плоскости 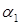. По формуле (2.4) найдем расстояние от точки  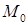до плоскости .

.

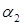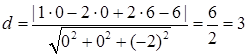Ответ: 3.

Прямая линия в пространстве.