Понятие об уравнении поверхности и линии в пространстве
Уравнением поверхности в пространстве с заданной декартовой системой координат Oxyz называют уравнение F ( x ; y ; z )=0, которому удовлетворяют все точки поверхности и только они.
Линию в пространстве можно рассматривать как линию пересечении двух поверхностей. В этом случае она задается системой двух уравнений:
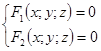 .
.
Если линию рассматривать как траекторию движения точки, то она задается параметрически уравнениями : 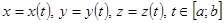
Плоскость и её уравнения
Докажем утверждение:
Если в пространстве задана произвольная плоскость 𝛑 и фиксирована произвольная декартова система координат Oxyz с ортонормированным базисом, то плоскость 𝛑 в этой системе координат определяется уравнением первой степени относительно x , y , z
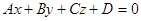
Доказательство. Положение плоскости в пространстве относительно выбранной прямоугольной системы координат вполне определяется какой-либо точкой 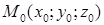 этой плоскости и ненулевым вектором
этой плоскости и ненулевым вектором 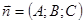 , перпендикулярным рассматриваемой плоскости. Для всякого ненулевого вектора
, перпендикулярным рассматриваемой плоскости. Для всякого ненулевого вектора 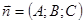 выполняется условие
выполняется условие 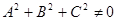 .
.
Всякий ненулевой вектор, перпендикулярный плоскости, называется нормальным вектором этой плоскости.
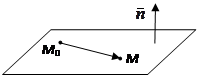 На плоскости 𝛑 возьмем произвольную точку
На плоскости 𝛑 возьмем произвольную точку 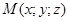 . Вектор
. Вектор 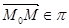 , следовательно, векторы
, следовательно, векторы 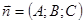 и
и 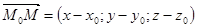 взаимно перпендикулярны, поэтому
взаимно перпендикулярны, поэтому 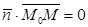 .
.
В координатной форме скалярное произведение векторов 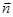 и
и 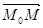
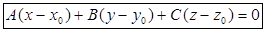 (2.1)
(2.1)
Уравнение (2.1) называется уравнением плоскости, заданной точкой 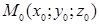 и нормальным вектором
и нормальным вектором 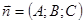 .
.
Раскрывая скобки в уравнении (2.1) и обозначив число 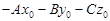 через D, получим уравнение
через D, получим уравнение
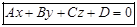 (2.2)
(2.2)
Уравнение (2.2) называется общим уравнением плоскости. Коэффициенты A, B, C являются координатами нормального вектора плоскости 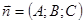 , x, y, z – текущие координаты, т.е. координаты любой точки, принадлежащей плоскости.
, x, y, z – текущие координаты, т.е. координаты любой точки, принадлежащей плоскости.
Справедливо и обратное утверждение. Всякое уравнение первой степени относительно переменных x , y , z определяет плоскость в заданной екартовой системе координат.
Пример 2.1 Даны три точки 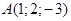 ,
, 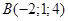 и
и 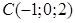 . Найти уравнение плоскости, проходящей через точку A и перпендикулярной вектору
. Найти уравнение плоскости, проходящей через точку A и перпендикулярной вектору 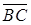 .
.
Решение.
Найдем координаты вектора 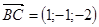 .
.
Так как по условию вектор 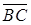 перпендикулярен плоскости, примем его за нормальный вектор этой плоскости. Используя уравнение 2.1, получим
перпендикулярен плоскости, примем его за нормальный вектор этой плоскости. Используя уравнение 2.1, получим
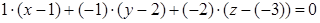 .
.
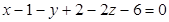
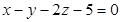 − искомое уравнение плоскости.
− искомое уравнение плоскости.
Общее уравнение плоскости 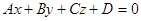 называется полным, если все его коэффициенты
называется полным, если все его коэффициенты 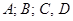 отличны от нуля. Если хотя бы один из коэффициентов равен 0, то уравнение называется неполным.
отличны от нуля. Если хотя бы один из коэффициентов равен 0, то уравнение называется неполным.
Рассмотрим частные случаи расположения плоскостей.
а) Если D=0, то 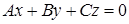 − плоскость проходит через начало координат.
− плоскость проходит через начало координат.
б) Если С=0, то 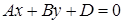 − плоскость параллельна оси Oz.
− плоскость параллельна оси Oz.
Если A=0, то 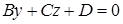 − плоскость параллельна оси Ox.
− плоскость параллельна оси Ox.
Если B=0, то 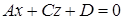 − плоскость параллельна оси Oy.
− плоскость параллельна оси Oy.
в) Если A=D=0, то 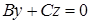 − плоскость проходит через ось Ox.
− плоскость проходит через ось Ox.
Если B=D=0, то 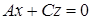 − плоскость проходит через ось Oy.
− плоскость проходит через ось Oy.
Если C=D=0, то 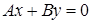 − плоскость проходит через ось Oz.
− плоскость проходит через ось Oz.
г) Если B=C=0, то 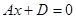 или
или 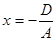 , то плоскость параллельна координатной плоскости yOz. Аналогично уравнения
, то плоскость параллельна координатной плоскости yOz. Аналогично уравнения 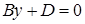 и
и 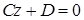 определяют плоскости, параллельные координатным плоскостям соответственно xOz и xOy.
определяют плоскости, параллельные координатным плоскостям соответственно xOz и xOy.
д) Если B=C=D=0, то Ax=0 или x=0. Плоскость совпадает с координатной плоскостью yOz. Аналогично уравнения By=0, Cz=0 или y=0, z=0 определяют координатные плоскости xOz, xOy соответственно.
Например,
1) 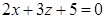
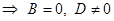 ,
, 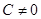 ,
, 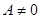 − плоскость параллельна оси Oy.
− плоскость параллельна оси Oy.
2) 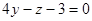
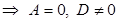 ,
, 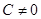 ,
, 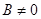 − плоскость параллельна оси Ox.
− плоскость параллельна оси Ox.
3) 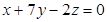
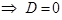 ,
, 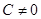 ,
, 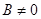 ,
, 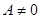 − плоскость проходит через начало координат.
− плоскость проходит через начало координат.
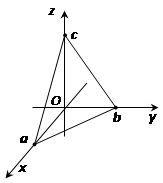
· Уравнение плоскости в отрезках
Рассмотрим полное общее уравнение плоскости.
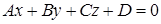
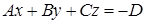
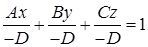
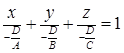
Пусть 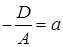 ,
, 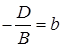 ,
, 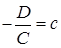 , тогда получим уравнение
, тогда получим уравнение
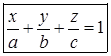 , (2.3)
, (2.3)
которое называется уравнением плоскости в отрезках, где a, b и c – величины направленных отрезков, отсекаемых плоскостью на координатных осях Ox, Oy и Oz соответственно.
Пример 2.2. Построить плоскость, которая задается уравнением 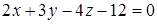 .
.
 Решение. Приведем общее уравнение плоскости к уравнению плоскости в отрезках.
Решение. Приведем общее уравнение плоскости к уравнению плоскости в отрезках.
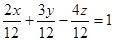
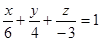
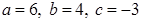 .
.
Пример 2. Плоскость проходит через точку 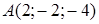 и отсекает отрезки на оси абсцисс
и отсекает отрезки на оси абсцисс 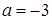 , на оси аппликат
, на оси аппликат 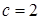 . Составить уравнение плоскости.
. Составить уравнение плоскости.
Решение. Воспользуемся уравнением (1.3).
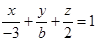
Точка A лежит на плоскости, т.е. ее координаты удовлетворяют уравнению плоскости
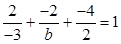 , откуда
, откуда 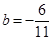 .
.
Следовательно, искомое уравнение 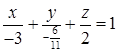 или
или 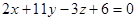 .
.
· Уравнение плоскости, проходящей через три данные точки
Если три точки 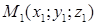 ,
, 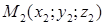 и
и 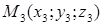 не принадлежат одной прямой, то через эти точки можно провести единственную плоскость.
не принадлежат одной прямой, то через эти точки можно провести единственную плоскость.
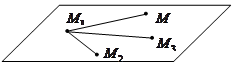 Так как векторы
Так как векторы 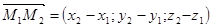 и
и 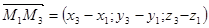 не коллинеарны, то точка
не коллинеарны, то точка 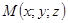 лежит в одной плоскости с точками
лежит в одной плоскости с точками 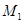 ,
, 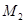 и
и 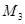 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  ,
, 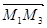 и
и 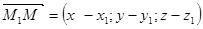 компланарны. Т.е. смешанное произведение векторов
компланарны. Т.е. смешанное произведение векторов 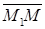 ,
, 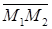 ,
, 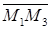 равно 0. Запишем условие компланарности трех векторов в координатной форме.
равно 0. Запишем условие компланарности трех векторов в координатной форме.
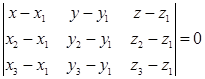 (2.4)
(2.4)
Уравнение (2.4) называется уравнением плоскости, проходящей через три точки.
В векторной форме это уравнение имеет вид: 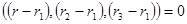 , где
, где 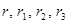 − радиус-векторы точек
− радиус-векторы точек 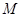 ,
, 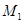 ,
, 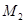 и
и 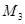 .
.
Пример 2.3 Найти общее уравнение плоскости, проходящей через три заданные точки 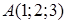 ,
, 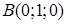 ,
, 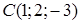 .
.
Решение. Воспользуемся уравнением (2.4).
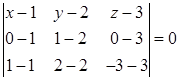
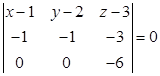
Разложим определитель по элементам первой строки:
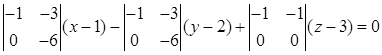
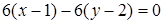
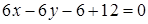
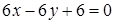
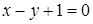 .
.
· Нормальное уравнение плоскости
Пусть дана плоскость 𝛑. Точка Р – точка пересечения перпендикуляра, опущенного из начала координат, на плоскость 𝛑 и плоскости 𝛑.
На прямой OP возьмем единичный вектор 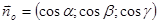 . Очевидно, что точка
. Очевидно, что точка 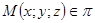 тогда и только тогда, когда
тогда и только тогда, когда 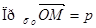 , где
, где 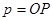 .
.
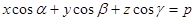
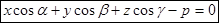
Общее уравнение плоскости 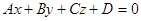 приводится к нормальному виду путем умножения на нормирующий множитель
приводится к нормальному виду путем умножения на нормирующий множитель 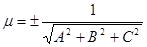 , взятый со знаком, противоположным знаку свободного члена D.
, взятый со знаком, противоположным знаку свободного члена D.
Угол между прямыми.
Если две прямые 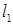 и
и 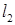 в пространстве заданы каноническими уравнениями
в пространстве заданы каноническими уравнениями 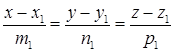 и
и 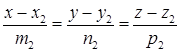 , то
, то
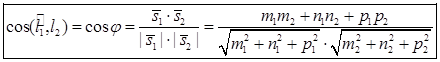 (5.1)
(5.1)
Пример 5.1 Найти угол между прямыми, заданными уравнениями
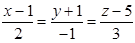 и
и 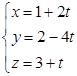 .
.
Решение. Найдем направляющие векторы прямых: 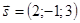 и
и 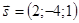 . По формуле (4.1) находим угол между прямыми.
. По формуле (4.1) находим угол между прямыми.
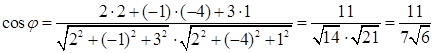 .
.
Угол 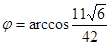 .
.
Решение.
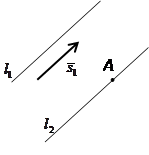 Т.к. прямые
Т.к. прямые 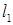 и
и 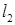 параллельны, то направляющий вектор
параллельны, то направляющий вектор 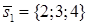 является также направляющим вектором для искомой прямой. Воспользуемся каноническими уравнениями (5.2)
является также направляющим вектором для искомой прямой. Воспользуемся каноническими уравнениями (5.2)
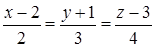 , откуда найдем параметрические уравнения
, откуда найдем параметрические уравнения 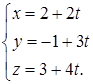
Понятие об уравнении поверхности и линии в пространстве
Уравнением поверхности в пространстве с заданной декартовой системой координат Oxyz называют уравнение F ( x ; y ; z )=0, которому удовлетворяют все точки поверхности и только они.
Линию в пространстве можно рассматривать как линию пересечении двух поверхностей. В этом случае она задается системой двух уравнений:
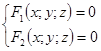 .
.
Если линию рассматривать как траекторию движения точки, то она задается параметрически уравнениями : 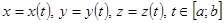
Плоскость и её уравнения
Докажем утверждение:
Если в пространстве задана произвольная плоскость 𝛑 и фиксирована произвольная декартова система координат Oxyz с ортонормированным базисом, то плоскость 𝛑 в этой системе координат определяется уравнением первой степени относительно x , y , z
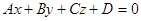
Доказательство. Положение плоскости в пространстве относительно выбранной прямоугольной системы координат вполне определяется какой-либо точкой 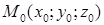 этой плоскости и ненулевым вектором
этой плоскости и ненулевым вектором 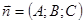 , перпендикулярным рассматриваемой плоскости. Для всякого ненулевого вектора
, перпендикулярным рассматриваемой плоскости. Для всякого ненулевого вектора 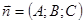 выполняется условие
выполняется условие 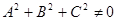 .
.
Всякий ненулевой вектор, перпендикулярный плоскости, называется нормальным вектором этой плоскости.
 На плоскости 𝛑 возьмем произвольную точку
На плоскости 𝛑 возьмем произвольную точку 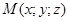 . Вектор
. Вектор 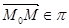 , следовательно, векторы
, следовательно, векторы 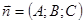 и
и 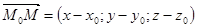 взаимно перпендикулярны, поэтому
взаимно перпендикулярны, поэтому 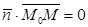 .
.
В координатной форме скалярное произведение векторов 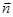 и
и 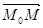
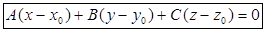 (2.1)
(2.1)
Уравнение (2.1) называется уравнением плоскости, заданной точкой 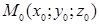 и нормальным вектором
и нормальным вектором 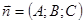 .
.
Раскрывая скобки в уравнении (2.1) и обозначив число 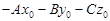 через D, получим уравнение
через D, получим уравнение
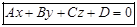 (2.2)
(2.2)
Уравнение (2.2) называется общим уравнением плоскости. Коэффициенты A, B, C являются координатами нормального вектора плоскости 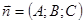 , x, y, z – текущие координаты, т.е. координаты любой точки, принадлежащей плоскости.
, x, y, z – текущие координаты, т.е. координаты любой точки, принадлежащей плоскости.
Справедливо и обратное утверждение. Всякое уравнение первой степени относительно переменных x , y , z определяет плоскость в заданной екартовой системе координат.
Пример 2.1 Даны три точки 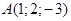 ,
, 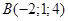 и
и 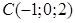 . Найти уравнение плоскости, проходящей через точку A и перпендикулярной вектору
. Найти уравнение плоскости, проходящей через точку A и перпендикулярной вектору 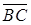 .
.
Решение.
Найдем координаты вектора 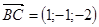 .
.
Так как по условию вектор 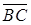 перпендикулярен плоскости, примем его за нормальный вектор этой плоскости. Используя уравнение 2.1, получим
перпендикулярен плоскости, примем его за нормальный вектор этой плоскости. Используя уравнение 2.1, получим
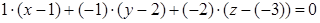 .
.
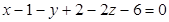
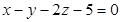 − искомое уравнение плоскости.
− искомое уравнение плоскости.
Общее уравнение плоскости 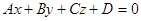 называется полным, если все его коэффициенты
называется полным, если все его коэффициенты 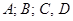 отличны от нуля. Если хотя бы один из коэффициентов равен 0, то уравнение называется неполным.
отличны от нуля. Если хотя бы один из коэффициентов равен 0, то уравнение называется неполным.
Рассмотрим частные случаи расположения плоскостей.
а) Если D=0, то 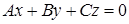 − плоскость проходит через начало координат.
− плоскость проходит через начало координат.
б) Если С=0, то 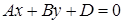 − плоскость параллельна оси Oz.
− плоскость параллельна оси Oz.
Если A=0, то 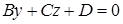 − плоскость параллельна оси Ox.
− плоскость параллельна оси Ox.
Если B=0, то 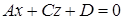 − плоскость параллельна оси Oy.
− плоскость параллельна оси Oy.
в) Если A=D=0, то 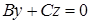 − плоскость проходит через ось Ox.
− плоскость проходит через ось Ox.
Если B=D=0, то 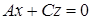 − плоскость проходит через ось Oy.
− плоскость проходит через ось Oy.
Если C=D=0, то 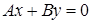 − плоскость проходит через ось Oz.
− плоскость проходит через ось Oz.
г) Если B=C=0, то 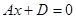 или
или 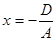 , то плоскость параллельна координатной плоскости yOz. Аналогично уравнения
, то плоскость параллельна координатной плоскости yOz. Аналогично уравнения 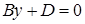 и
и 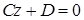 определяют плоскости, параллельные координатным плоскостям соответственно xOz и xOy.
определяют плоскости, параллельные координатным плоскостям соответственно xOz и xOy.
д) Если B=C=D=0, то Ax=0 или x=0. Плоскость совпадает с координатной плоскостью yOz. Аналогично уравнения By=0, Cz=0 или y=0, z=0 определяют координатные плоскости xOz, xOy соответственно.
Например,
1) 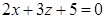
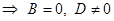 ,
, 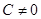 ,
, 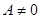 − плоскость параллельна оси Oy.
− плоскость параллельна оси Oy.
2) 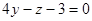
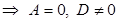 ,
, 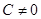 ,
, 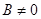 − плоскость параллельна оси Ox.
− плоскость параллельна оси Ox.
3) 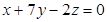
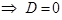 ,
, 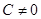 ,
, 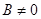 ,
, 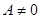 − плоскость проходит через начало координат.
− плоскость проходит через начало координат.
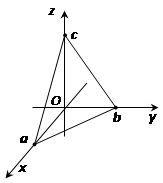
· Уравнение плоскости в отрезках
Рассмотрим полное общее уравнение плоскости.
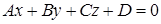
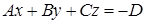
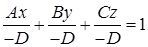
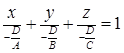
Пусть 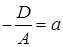 ,
, 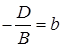 ,
, 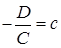 , тогда получим уравнение
, тогда получим уравнение
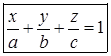 , (2.3)
, (2.3)
которое называется уравнением плоскости в отрезках, где a, b и c – величины направленных отрезков, отсекаемых плоскостью на координатных осях Ox, Oy и Oz соответственно.
Пример 2.2. Построить плоскость, которая задается уравнением 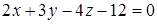 .
.
 Решение. Приведем общее уравнение плоскости к уравнению плоскости в отрезках.
Решение. Приведем общее уравнение плоскости к уравнению плоскости в отрезках.
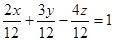
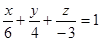
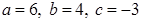 .
.
Пример 2. Плоскость проходит через точку 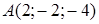 и отсекает отрезки на оси абсцисс
и отсекает отрезки на оси абсцисс 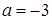 , на оси аппликат
, на оси аппликат 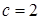 . Составить уравнение плоскости.
. Составить уравнение плоскости.
Решение. Воспользуемся уравнением (1.3).
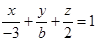
Точка A лежит на плоскости, т.е. ее координаты удовлетворяют уравнению плоскости
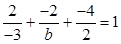 , откуда
, откуда 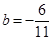 .
.
Следовательно, искомое уравнение 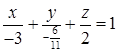 или
или 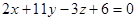 .
.
· Уравнение плоскости, проходящей через три данные точки
Если три точки 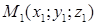 ,
, 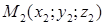 и
и 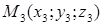 не принадлежат одной прямой, то через эти точки можно провести единственную плоскость.
не принадлежат одной прямой, то через эти точки можно провести единственную плоскость.
 Так как векторы
Так как векторы 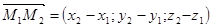 и
и 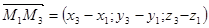 не коллинеарны, то точка
не коллинеарны, то точка 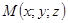 лежит в одной плоскости с точками
лежит в одной плоскости с точками 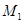 ,
, 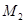 и
и 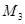 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  ,
, 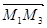 и
и 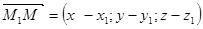 компланарны. Т.е. смешанное произведение векторов
компланарны. Т.е. смешанное произведение векторов 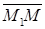 ,
, 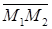 ,
, 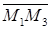 равно 0. Запишем условие компланарности трех векторов в координатной форме.
равно 0. Запишем условие компланарности трех векторов в координатной форме.
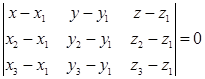 (2.4)
(2.4)
Уравнение (2.4) называется уравнением плоскости, проходящей через три точки.
В векторной форме это уравнение имеет вид: 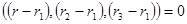 , где
, где 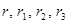 − радиус-векторы точек
− радиус-векторы точек 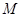 ,
, 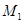 ,
, 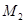 и
и 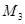 .
.
Пример 2.3 Найти общее уравнение плоскости, проходящей через три заданные точки 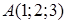 ,
, 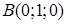 ,
, 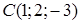 .
.
Решение. Воспользуемся уравнением (2.4).
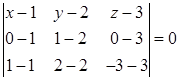
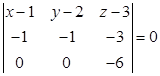
Разложим определитель по элементам первой строки:
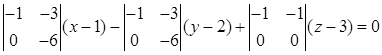
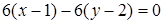
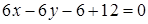
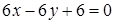
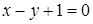 .
.
· Нормальное уравнение плоскости
Пусть дана плоскость 𝛑. Точка Р – точка пересечения перпендикуляра, опущенного из начала координат, на плоскость 𝛑 и плоскости 𝛑.
На прямой OP возьмем единичный вектор 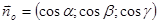 . Очевидно, что точка
. Очевидно, что точка 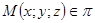 тогда и только тогда, когда
тогда и только тогда, когда 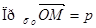 , где
, где 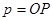 .
.
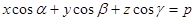
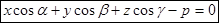
Общее уравнение плоскости 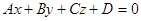 приводится к нормальному виду путем умножения на нормирующий множитель
приводится к нормальному виду путем умножения на нормирующий множитель 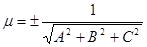 , взятый со знаком, противоположным знаку свободного члена D.
, взятый со знаком, противоположным знаку свободного члена D.
Дата: 2018-11-18, просмотров: 855.