Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Существуют следующие виды виброиспытаний [1]:

— испытания на вибропрочность (способность изделия сохранять прочность в условиях вибрации);

— испытания на виброустойчивость (способность изделия при вибрации выполнять свои функции и сохранять параметры в пределах установленных норм).

При испытаниях на одной частоте предусматривается выявление производственных дефектов изготовления изделия.

Испытания на вибропрочность предусматривают проверку способности изделия противостоять разрушающему влиянию вибрационных воздействий и выполнять свои функции при сохранении параметров после механического воздействия в пределах значений, указанных в ТУ на изделие. При испытаниях на вибропрочность изделие в заданном диапазоне частот подвергается воздействию гармонической вибрации с плавной разверткой частоты, а также широкополосной, узкополосной или смешанной вибрации. Общее время испытаний разделяют на равные промежутки, в течение которых осуществляют испытания на каждой выбранной частоте.

При испытаниях на виброустойчивость определяется способность изделия выполнять свои функции и сохранять свои основные параметры в условиях вибрации в заданном диапазоне частот и ускорений в пределах, указанных в нормативных документах на изделие. Испытания под воздействием вибрации проводятся в трех взаимно перпендикулярных направлениях.

В процессе испытаний измеряются параметры изделия. Для проверки виброустойчивости выбирают такие параметры испытываемых изделий, по изменению которых можно судить о виброустойчивости, например, уровень виброшумов, искажение выходного сигнала, нестабильность сопротивлений и т. д. Во время испытаний изделие и его отдельные элементы периодически проверяют на отсутствие механических повреждений. Испытания изделия на виброустойчивость проводят в рабочем режиме с одновременным подключением измерительных приборов, посредством которых контролируют работоспособность и измеряют параметры изделия при воздействии вибрации. Степень жесткости вибрационных испытаний определяется сочетанием следующих трех параметров: частотного диапазона, амплитуды вибрации и величины ускорения.

Степень жесткости вибрации желательно выбирать на основе реальных вибрационных характеристик, если они известны, или с использованием рекомендаций, изложенных в соответствующих ГОСТах, если они не известны.

Основные требования к испытаниям различных изделий и средствам испытаний сформулированы в рекомендациях международных и государственных стандартов. В общем виде эти требования можно свести к следующим:

— возможность проведения испытаний на гармоническую (синусоидальную и полигармоническую), случайную (узкополосную и широкополосную) и смешанную (гармоническую и случайную) вибрацию;

— обеспечение воспроизводимости результатов испытаний, исключающей неоднозначность заключения;

— возможность учета особенностей характеристик испытуемого изделия и способов его крепления;

— простота и удобство в управлении заданным испытательным режимом, возможность ручного и автоматического управления;

— обеспечение воспроизведения и измерения параметров вибрации в диапазоне частот 0. . . 10 кГц, ускорении до 1000 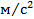, перемещений от 0,1 мкм до 1 м, спектральной плотности ускорения до 1,0 ;

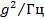— обеспечение точности измерения частоты менее 50 Гц ±(1 . . . 2) Гц и более 50 Гц ±(2 . . . 3) %; перемещения ±(10 . . . 20) %; ускорения ±(10 . . . 20) %; спектральной плотности ускорения ±(1,5 . . . 3,0) дБ;

— обеспечение точности (0,5. . . 2 дБ) поддержания ускорения (перемещения) постоянным при динамическом диапазоне регулирования 10. . . 60 дБ.

Существуют три метода испытаний: стендовые, полунатурные (использование данных натурных испытаний изделия на стенде) и натурные.

Стендовые, или лабораторные, вибрационные испытания осуществляют на вибростендах, которые приближенно воспроизводят реальные динамические нагрузки, действующие на изделия. При таких испытаниях проверяют качество изготовления и долговечность изделия. Они должны проводиться при динамических нагрузках, соответствующих реальным условиям эксплуатации изделия, а если их нет, то при несколько повышенных нормах нагрузок, которые определят по прототипам, исходя из условий эксплуатации изделия.

Например, радиоэлектронное изделие, которое должно эксплуатироваться при вибрационных нагрузках, должно выдерживать воздействие вибрации с амплитудой ускорений до 200 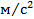 в диапазоне частот 5. . . 5000 Гц.

Для выполнения поставленных требований при лабораторных испытаниях используются вибрационные установки (рис. 16.1), в структурную схему которых входят:

— вибростенд (вибровозбудитель) 4, преобразующий энергию любого вида в энергию механических колебаний (в вибрацию);

— генератор испытательных (управляющих) сигналов 2, создающий управляющее воздействие на вибростенд, соответствующее заданному характеру вибрации и режиму испытаний;

— усилитель мощности 3, предназначенный для получения требуемого значения вынуждающей силы.

В конструкцию вибростенда 4 входит как неподвижная часть, так и подвижная система, совершающая вибрационное движение. Устойчивое равновесие и ориентацию подвижной системы относительно неподвижной части обеспечивает система подвески. Испытуемое изделие устанавливается и закрепляется для передачи ему вибрации на конструктивной части подвижной системы, называемой столом 5.

 

 

 

Рис. 16.1. Структурная схема вибрационной установки:

1 — система управления; 2 — генератор испытательных сигналов; 3 — усилитель мощности; 4 — вибростенд; 5 — стол вибростенда; 6 — контрольная точка; 7 — контрольный ВИП; 8 — измерительная точка; 9 — испытуемое изделие; 10 — измерительный ВИП; 11 — средства измерения, анализа и обработки результатов измерений

 

Для получения информации о воздействии вибрации в процессе испытаний используют виброизмерительные преобразователи (ВИП), размещаемые в двух или более точках. Различают две основные точки: контрольную и измерительную. Контрольная точка 6 располагается в том месте, относительно которого должно проводиться измерение значений параметров вибрации испытуемого изделия (на столе вибростенда, на приспособлении, на самом изделии), причем она должна находиться как можно ближе к одной из точек крепления и быть с ней жестко связана. Сигнал с контрольного ВИП 7, расположенного в контрольной точке, используется в системе управления 1, обеспечивающей поддержание значений параметров вибрации на определенном уровне. Возможно использование нескольких контрольных точек. В этом случае сигналы, снимаемые с них с помощью ВИП, подвергаются непрерывному арифметическому усреднению или обработке специальной сравнивающей аппаратурой.

Измерительная точка 8 располагается в том месте на испытуемом изделии 9, где значения параметров вибрации определяют исход испытаний. В точку 8 помещают ВИП 10, сигнал с которого подводится к средствам измерения, анализа и обработки результатов измерений 11. При испытаниях микроминиатюрных изделий желательно над указанным местом располагать бесконтактный ВИП.

Таким образом, результаты испытаний оцениваются значениями параметров вибрации, полученными в измерительной точке при условии обеспечения заданных значений в контрольной точке.

Вибростенд — вибрационная испытательная или калибровочная машина, к рабочей платформе (вибростолу) которой прикрепляются изделия для вибрационных испытаний или датчики виброизмерительной аппаратуры, подвергаемой калибровке (тарированию) или поверке. Существуют вибростенды универсальные и специального назначения, например, для проведения модального анализа, инерционные, ударные вибростенды. Амплитуду и частоту колебаний платформы универсального вибростенда можно плавно изменять в определенном диапазоне с помощью системы управления виброиспытаний.

Специализированное программное обеспечение (ПО) позволяет автоматизировать процесс испытаний, а также максимально приблизить сами испытания к реальным условиям окружающей среды. В состав ПО входят программы для формирования и измерения синусоидальных, случайных и ударных воздействий. Направление вибрации может быть вертикальным или горизонтальным.

Система амортизации корпуса вибростендов обеспечивает виброизоляцию в рабочем диапазоне частот и устраняет необходимость использования специального фундамента в большинстве случаев применения (при вертикальной и горизонтальной вибрации). Системы охлаждения вибростендов — воздушные или водяные.

Широкое распространение получили электродинамические, электрогидравлические и механические вибростенды, пьезоэлетрические и другие виды вибростендов. Их применение определяется требованиями к виду вибрации и к значению их параметров. Электродинамические вибростенды позволяют создавать колебания более высокочастотные (5. . . 10 000 Гц), чем электрогидравлические (0. . . 1000 Гц). Механические вибростенды применяют в системах, предназначенных для испытания методом фиксированных частот.

Основным недостатком всех видов вибростендов является зависимость их передаточной функции от частоты и нагрузки, что существенно усложняет задачу воспроизведения заданных параметров вибрации при испытаниях в широком диапазоне частот. Поэтому для реализации любого метода испытаний требуются специальные способы компенсации изменений передаточной функции при изменении частоты и нагрузок.

В основу работы электродинамических стендов положен электродинамический принцип возбуждения колебаний. Сила, вызывающая вибрацию подвижной системы, возникает в результате взаимодействия переменного электрического тока, протекающего по проводнику с постоянным магнитным потоком, в котором он находится. Питание подвижной системы стенда осуществляется от задающего генератора через усилительное устройство, обеспечивающее усиление сигнала генератора по мощности. Сигнал обратной связи, соответствующий величине получаемых ускорений, поступает в пульт управления от датчика ускорений, установленного на столе вибратора.

Испытуемое изделие совместно с приспособлением должно жестко крепиться на платформе виброустановки таким образом, чтобы общий центр тяжести их лежал на оси установки, т. е. на линии действия возбуждающей силы.

Частоты собственных колебаний платформы и испытуемого изделия с приспособлением должны лежать вне диапазона, в котором ведутся испытания. При испытаниях тяжелых изделий для компенсации статического прогиба упругой диафрагмы вибростенда применяют разгрузку с помощью, например, амортизационных шнуров.

Компания EMIC Corp. (Япония) проектирует и выпускает все значимые части электродинамических вибростендов, а именно:

— комбинированные установки (системы комплексного воздействия вибрация–удары–тепло–холод–термоудар–влажность; такое сочетание внешних воздействующих факторов очень точно воспроизводит реальные условия эксплуатации изделий);

— универсальные электродинамические вибростенды общего назначения с выталкивающим усилием до 60 кН включительно, которые применяются для проведения испытаний на вибропрочность и вибростойкость на многократные и одиночные удары и имеют воздушное охлаждение;

— мощные вибростенды с выталкивающим усилием более 60 кН (предназначены для длительной работы при больших нагрузках, испытаний габаритных образцов, изделий в сборе и нестандартных конструкций);

— малые вибростенды (служат для определения резонансов миниатюрных изделий и калибровки первичных преобразователей движения, скорости и ускорения; подвижная часть выполнена из керамики, позволяет реализовывать частоты до 30 кГц);

— вибростенды с увеличенной виброскоростью; имеют выталкивающее усилие до 60 кН включительно (для обеспечения проведения испытаний со специальными требованиями по виброскорости);

— вибростенды с увеличенным размахом виброперемещений.

Гидравлические виброустановки основаны на использовании гидравлических вибровозбудителей, которые создают колебания рабочего стола под действием переменного давления, вызванного пульсирующим потоком рабочей жидкости. Гидравлические вибровозбудители сообщают колебания рабочему столу вибростенда вследствие использования пульсирующего источника рабочей жидкости, либо прерывания потока рабочей жидкости постоянного расхода с помощью золотниковых устройств. Золотниковыми устройствами может управлять внешний привод, либо сам вибровозбудитель в соответствии с положением его исполнительного органа. Гидравлические виброустановки позволяют генерировать колебания, форма которых описывается различными функциями времени, соответствующими нагрузке, встречающейся в реальных условиях. К достоинствам этих вибростендов относятся:

— возможность получения большой вынуждающей силы (до десятков тонн);

— широкий диапазон амплитуд перемещений (от долей миллиметров до десятков сантиметров);

— малые паразитные электромагнитные излучения.

Электромеханические вибростенды — простое, надежное, эффективное средство проведения относительно несложных отбраковочных испытаний комплектующих и изделий на воздействие синусоидальной вибрации в процессе производства. Синусоидальная вибрация обладает большой эффективностью выявления скрытых дефектов благодаря своим свойствам. Однокомпонентные электромеханические вибростенды получили широкое распространение благодаря дешевизне, простоте и надежности. Применяются для проведения технологической вибрации и отбраковки практически на всех этапах производственного цикла изделия. Многокомпонентные электромеханические вибростенды

— двух- и трехкомпонентные электромеханические вибростенды применяются для ответственной отбраковки изделий и для оценки надежности изделия при транспортировке.

При проведении лабораторных вибрационных испытаний вначале определяют резонансы в заданном диапазоне частот и испытывают на вибропрочность на фиксированных частотах (контрольные испытания). В дальнейшем изделие испытывают на вибропрочность в заданном диапазоне частот и затем на виброустойчивость. После конструктивной доработки изделие вновь подвергают вибрационным испытаниям. При определении резонансных частот изделие подвергают воздействию гармонической вибрации при пониженных ускорениях, как правило, не превышающих 20 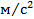 в диапазоне частот 10. . . 150 Гц.

После регистрации резонансных частот назначают одну или несколько нерезонансных частот, при которых проводят контрольные испытания изделия на воздействие ускорения при различной длительности испытания.

Испытания на одной частоте предусматривают выявление производственных дефектов изготовления изделия, поэтому при контрольных испытаниях его не следует испытывать на резонансной частоте. Если испытания проводились на резонансной частоте, то в случае обнаружения какого-либо дефекта трудно установить причину разрушения, так как при длительных испытаниях разрушение может быть вызвано действием резонансных эффектов, а не дефектом изготовления изделия. Поэтому испытания рекомендуется начинать с определения резонансных частот при пониженных воздействующих ускорениях гармонической вибрации.

Наиболее адекватными являются натурные испытания изделия, однако их организация наиболее сложна и дорогостояща. Из-за сложности возмущающих колебаний возникают также трудности анализа вибрации и выявления причин, вызывающих поломки и нарушения в работе изделия.

Применяют также полунатурные испытания, используя записи натурных испытаний на объекте, а также данные, переданные по каналам телеметрии, для дальнейшего воспроизведения этих условий при стендовых испытаниях.

С помощью вибростендов проводятся испытания на вибропрочность и виброустойчивость изделий машиностроительных, электрорадиотехнических и других отраслей, а также для исследования их динамических характеристик, надежности, ресурса. С целью выявления резонансных процессов в испытываемых изделиях система управления испытательного вибростенда обеспечивает сканирование частоты во всем диапазоне (от минимальной до максимальной) при поддержании заданных ускорений. Задание и изменение параметров осуществляется оператором испытательного вибростенда вручную либо автоматически по заданной программе. Предусмотрен также «вход» от внешнего функционального генератора с записью воздействий на испытываемое изделие в условиях реальной эксплуатации или транспортирования.

Основными методами виброиспытаний являются следующие:

— фиксированной и качающейся частоты;

— полигармонического возбуждения;

— широкополосного случайного возбуждения;

— узкополосного случайного возбуждения;

— смешанной вибрации (синусоидальной и случайной);

— многокомпонентной вибрации;

— многоканального возбуждения вибрации.

Далее рассмотрим некоторые из них.

Метод фиксированных частот заключается в последователъном воздействии механических колебаний определенной частоты и амплитуды на испытуемое изделие в требуемом диапазоне частот. При этом вручную плавно изменяют частоту вибрации от низшего значения до высшего и обратно с заданной амплитудой и регистрируют механические резонансы и нестабильность технических характеристик изделия (виброустойчивость), т. е. этот метод позволяет:

— определить резонансные частоты;

— проводить испытания на вибропрочность и виброустойчивость (выявление нестабильности технических характеристик изделия);

— выявить механические дефекты.

Испытания проводят в несколько этапов:

— выявление резонансных частот;

— испытания на вибропрочность;

— повторное, окончательное выявление резонансных частот.

На резонансных частотах проводят испытания на вибропрочность, а если не удалось выявить эти частоты, то на определенных частотах с заданными амплитудой колебаний и продолжительностью. Испытания методом фиксированных частот на заранее определенных частотах механического резонанса испытуемых изделий требуют предварительного выявления указанных частот, что для сложных многоэлементных конструкций представляет некоторую сложность. Испытуемое изделие последовательно подвергают воздействию вибрации на частотах резонанса, выдерживая его в каждом режиме в течение некоторого времени. Достоинством указанного метода испытаний является то, что он проводится на наиболее опасных для испытуемого изделия частотах вибрации. К недостаткам можно отнести сложность автоматизации процесса испытаний, поскольку в процессе их проведения резонансные частоты могут несколько изменяться.

Структурная схема испытаний на фиксированных частотах имеет следующий вид (рис. 16.2).

Другие недостатки этого метода:

— при испытании на вибропрочность изделие может быть недоиспытано из-за невозможности выявления неявных резонансов;

— сложность контроля амплитуды и частоты;

— наличие последовательного процесса возбуждения резонансов в отличие

 от реальных условий, при которых происходит одновременное возбуждение резонансов.

 

 

Рис. 16.2. Структурная схема испытаний на фиксированных частотах:

1 — задающий генератор; 2 — усилитель; 3 — вибратор; 4 — изделие; 5 — преобразователь; 6 — виброизмерительная аппаратура

 

 

 

Рис. 16.3. Структурная схема устройства для определения резонансных частот пьезоэлектрическим методом: 1 — стол вибростенда; 2 — приспособление для крепления изделия; 3 — испытываемое изделие; 4, 10 — пьезопреобразователь; 5, 9 – согласующее устройство; 6, 8 — измерительное устройство; 7 — регистрирующее устройство

 

Структурная схема устройства для определения резонансных частот пьезоэлектрическим методом имеет вид (рис. 16.3).

Данный метод отработан, широко используется на практике и обеспечивает высокую точность измерений при условии, когда размеры и масса испытываемого изделия в 10 и более раз превышает размеры и массу пьезопреобразователя.

Метод качающейся частоты позволяет автоматизировать процедуру испытаний и проводить их на всех частотах в заданном диапазоне. Этот метод заключается в циклическом прохождении заданного диапазона частот от нижней частоты до верхней и обратно при постоянстве заданных параметров вибрации в течение определенного времени. При этом число качания устанавливается в нормативно-технической документации (обычно рекомендуется ряд — 1, 2, 5,10, 20, 50, 100).

Структурная схема испытаний методом качающейся частоты с сопровождающим фильтром приведена на рис. 16.4.

Испытания проводят при постоянном уровне ускорения, скорости или перемещения рабочего стола вибратора. Например, при постоянном уровне перемещения на низких частотах, а затем при постоянном уровне ускорения на более высоких частотах. Переход от режима вибрации при постоянном перемещении к режиму вибрации при постоянном ускорении осуществляется с частотой, которая зависит от условий эксплуатации изделия и обычно находится в диапазоне 10. . . 500 Гц.

 

Рис. 16.4. Структурная схема испытаний методом качающейся частоты с

сопровождающим фильтром: 1 — вибропреоразователь; 2 — согласующее устройство; 3 — сопровождающий фильтр; 4 — управляемый генератор; 5 — усилитель мощности; 6 — вибростенд

 

Основными параметрами, характеризующими метод качающейся частоты, являются: изменение частоты в рабочем диапазоне частот в одном направлении и обратном (время одного цикла качания 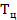), скорость изменения частот (скорость качания 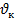), а также продолжительность испытаний .

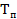Наличие нелинейных механических элементов в конструкциях испытуемых изделий приводит к тому, что, хотя данное изделие возбуждают чисто синусоидальной вибрацией, возникают колебания на частотах гармоник и, следовательно, сигнал управления, используемый для регулирования уровня вибраций, будет содержать гармоники, приводящие к ослаблению колебаний на основной частоте. В связи с этим в цепь обратной связи системы управления иногда включают так называемый сопровождающий фильтр, обеспечивающий подведение к схеме обратной связи сигнала на основной частоте, возбуждаемой вибростендом. При этом достигается синхронная фильтрация сигнала управления, исключающая попадание на генератор напряжения частот вибрации помех и высших гармоник. Сопровождающий фильтр является узкополосным, средняя частота его полосы пропускания автоматически сопровождает основную частоту или одну из гармоник периодического сигнала. Средняя частота полосы пропускания, на которую настраивается фильтр, может находиться в диапазоне частот 2. . . 2000 Гц. Эффективная фиксированная относительная ширина полосы пропускания фильтра определяется в процентах частоты настройки во всем рабочем частотном диапазоне. Сопровождающий фильтр может иметь несколько постоянных значений относительно ширины полосы пропускания.

Зачастую качание частоты осуществляется по логарифмическому закону, причем рекомендуемая скорость 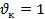октава/мин. Время цикла качания  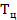должно определяться в зависимости от заданной степени жесткости испытаний, а также по специальному графику, позволяющему определить время изменения частоты в диапазоне.

При линейном законе изменения частоты время одного цикла качания частоты 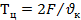,  где F — диапазон рабочих частот вибрации.

Стабилизация параметров вибрации в процессе качания частоты осуществляется таким образом, чтобы в случае увеличения амплитуды колебаний, фиксируемой вибропреобразователем, автоматически уменьшалась мощность, подводимая к вибростенду до установления исходного уровня.

Из-за нелинейности испытуемых изделий и наличия переходных процессов, происходящих в них, получаемая в режиме качающейся частоты резонансная кривая, называемая динамической, имеет ряд отличий от статической резонансной кривой, снятой методом фиксированных частот [1]:

— максимальная амплитуда колебаний при резонансе в динамическом режиме меньше, чем в статическом (стационарном) режиме;

— максимум динамической характеристики наблюдается позднее, чем статической, т. е. он смещается по шкале частоты в сторону качания;

— амплитуды колебаний нарастают плавно при подходе к резонансу, а убывают с убыстрением с течением времени, что объясняется биениями, возникающими между свободными колебаниями изделия и вынужденными колебаниями, создаваемыми вибростендами (в результате динамическая резонансная кривая получается асимметричной — левый скат оказывается более пологим);

— полоса пропускания динамической резонансной кривой оказывается шире, чем у статической, и при этом тем больше, чем быстрее изменяется частота.

Важным показателем метода качающейся частоты является скорость качания частоты. При большой скорости качания динамическая резонансная кривая в большей степени отличается от статической, а следовательно, оценка свойств испытуемого изделия будет проводиться с большими погрешностями.

Амплитуда резонансных колебаний изделия достигает меньших значений, чем при малой скорости, а также возможны пропуски (необнаружение) резонансов, возникающих в изделии. При выборе малой скорости качания длительное прохождение диапазона рабочих частот может вызвать повреждение испытуемого изделия на частотах резонанса и увеличение длительности испытаний.

Достоинством метода качающейся частоты является возможность определения собственных частот и амплитуд перемещения или ускорения при механических резонансах испытуемых изделий в рабочем диапазоне частот, знание которых позволяет принять необходимые меры для повышения надежности изделия.

Недостатком метода является то, что в каждый данный момент времени на изделие воздействуют одночастотные синусоидальные колебания, а не спектр частот, как при реальных условиях эксплуатации.

Метод управления режимом испытаний с компенсацией влияния импеданса не учитывает влияния механических импедансов испытуемого изделия и подвижной части вибратора. При этом предполагают, что импеданс изделия нулевой или импеданс основания бесконечно большой, поэтому испытуемое изделие не оказывает никакого влияния на источник возбуждения.

Метод виброиспытаний на полигармоническую вибрацию предусматривает воспроизведение сложногармонических вибрационных воздействий, наиболее часто встречающихся в условиях эксплуатации изделий. Этот метод основан на том, что все периодические сложногармонические процессы раскладываются в ряд Фурье. Процессы формируются генераторами синусоидальных сигналов c необходимой регулировкой фазовых сдвигов между этими сигналами, при этом задаются определенными значениями амплитуд и частот синусоидальных составляющих. Метод достаточно прост, отличается от метода испытаний на синусоидальную вибрацию в основном числом задающих генераторов синусоидальных сигналов и является переходным этапом между испытаниями на синусоидальную и случайную вибрацию.

Метод испытаний на воздействие случайной широкополосной вибрации.

В большинстве случаев реальные вибрационные процессы имеют случайный характер. Спектры реальной вибрации непрерывны, мгновенные значения амплитуд спектральных составляющих могут быть описаны только статистически. При испытаниях на воздействие случайной широкополосной вибрации все резонансные частоты испытуемого изделия возбуждаются одновременно, что позволяет выявить их взаимное влияние, которое нельзя определить при других видах испытаний.

Для проведения испытаний предварительно по результатам обработки реализаций случайного процесса, определяют числовые характеристики, а затем в контрольной точке изделия создают широкополосную случайную вибрацию, числовые характеристики которой должны быть близки к полученным при экспериментальном исследовании. В качестве характеристик подобия процессов обычно принимают спектральную плотность мощности или дисперсию вибрационных ускорений в заданной полосе частот, так как эти величины характеризуют реакцию изделия. На вибростенде в лаборатории воспроизводят одну из реализаций случайного процесса или процесс с заданными числовыми характеристиками.

При этом требуется относительно сложное и дорогостоящее оборудование.

При использовании метода испытаний на воздействие случайной широкополосной вибрации предусматривается постоянная плотность энергии каждой гармонической составляющей колебательного процесса, для чего на изделие воздействует «белый шум» и испытание проводят при определенных значениях среднего квадратического ускорения. Программа испытаний задается в виде графика спектральной плотности ускорения (рис. 16.5).

 

Рис. 16.5. График спектральной плотности ускорения

Структурная схема испытаний представлена на рис. 16.6.

В качестве сигнала возбуждения задающего устройства используется сигнал «белого шума», подаваемый на многочисленные фильтры фиксированной частоты, перекрывающие спектры частот сигнала возбуждения. Осуществление метода требует сложного и дорогостоящего оборудования, поэтому он зачастую заменяется более простым по технической реализации методом случайной вибрации со сканированием полосы частот.

К достоинствам испытаний на широкополосную случайную вибрацию можно отнести: близость к механическим воздействиям при реальной эксплуатации; моделирование статистического характера вибрации; возможность выявления всех эффектов механического взаимодействия различных элементов конструкции; наименьшую продолжительность испытаний. К недостаткам относятся: высокая стоимость и сложность используемого оборудования, трудоемкость проведения испытаний.

 

Рис. 16.6. Структурная схема испытаний методом ШСВ:

1 — генератор шума; 2 — блок фильтров; 3 — усилитель; 4 — вибратор; 5 — изделие; 6 — преобразователь; 7 — виброизмерительная аппаратура; 8 — анализирующее устройство; 9 — регистрирующее устройство

 

Метод испытаний на воздействие случайной узкополосной вибрации основан на замене широкополосного случайного возбуждения с низким уровнем спектральной плотности ускорений более интенсивным узкополосным возбуждением с медленной перестройкой фильтра по частоте. Критерием замены испытаний на широкополосную случайную вибрацию испытаниями на узкополосную с переменной средней частотой (сканирование узкополосного сигнала по частоте) является идентичность распределения пиковых ускорений и напряжений на изделии. Идентичность в распределении ускорений и напряжений можно получить, если средняя частота сканирующего узкополосного сигнала изменяется по логарифмическому закону и среднеквадратичное значение ускорения узкополосного спектра возрастает как корень квадратный из частоты. При постоянной полосе сканирования шумового сигнала это увеличение будет соответствовать 3 дБ/окт. В этом случае необходимо поддерживать постоянным закон изменения первоначального заданного уровня ускорения от частоты. Заданный режим контролируют по градиенту ускорения 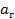. При этом градиент ускорения поддерживается постоянным.

Случайная вибрация в этом случае возбуждается в узкой полосе частот, центральная частота которой по экспоненциальному закону медленно сканирует по диапазону частот в процессе испытаний от минимального до максимального и наоборот. Таким образом, в данном методе реализовано компромиссное решение методов испытаний широкополосным сигналом и синусоидальным с изменяющейся частотой.

Для обеспечения эквивалентности методов испытаний широкополосным сигналом и синусоидальным с изменяющейся частотой должно выполняться условие:

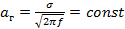                                                                                             (16.1)

где 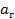— градиент ускорения; σ — среднее квадратическое ускорение вибрации в узкой полосе частот, g; f — центральная частота полосы, Гц.

Градиент ускорения определяется:

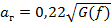                                                                                                (16.2)

где G(f) — спектральная плотность ускорения при испытании методом широкополосной случайной вибрации.

Структурная схема испытаний методом случайной вибрации со сканированием полосы частот показана на рис. 16.7.

Метод испытаний на воздействие случайной узкополосной вибрации имеет ряд преимуществ перед методом испытаний на воздействие случайной широкополосной вибрации:

— меньше затрат, более низкая стоимость приборов контроля и системы усиления сигнала до требуемого уровня возбуждения вибрации;

— быстрое установление и изменение полосы частот, в которых испытывается изделие;

— возможность снижения уровня возбуждения приблизительно в 3 раза.

Недостаток этого метода — медленное изменение средней частоты спектра при возбуждении последовательных резонансов испытываемого изделия, тогда как в случае возбуждения широкополосным спектром эти резонансы возбуждаются одновременно.

 

Рис. 16.7. Структурная схема испытаний методом случайной вибрации со сканированием полосы частот:

1 — генератор; 2 — полосовой фильтр; 3 — усилитель с автоматическим регулированием уровня; 4 — усилитель мощности; 5 — вибратор; 6 — изделие; 7 — преобразователь; 8 — виброизмерительная аппаратура

Лекция № 17. Акустическая эмиссия. Физические основы. Часть первая

Согласно [1], акустическая эмиссия (АЭ) — это явление генерации волн напряжения (упругих волн) при локальной перестройке структуры исследуемых объектов.

Акустическая эмиссия возникает в результате динамической перестройки структуры материала и представляет собой поток импульсов упругой энергии, имеющий характер ультразвуковых волн, испускаемых источником той или иной природы и принимаемых на поверхности изделия преобразователем АЭ (ПАЭ). Акустические поля, возникающие в металле при АЭ, имеют очень небольшую интенсивность перемещения. Это позволяет использовать фундаментальные решения волновых задач, суммируя или интегрируя их в зависимости от дискретности или непрерывности модели источника. Благодаря этому все проявления нелинейности и нестационарности АЭ процесса можно отнести на счет условий распространения сигналов АЭ.

На распространение сигналов АЭ влияют:

— среда (материал), по которой распространяется волна;

— поля внешних напряжений, являющиеся источником энергии для инициации АЭ, которые описываются начальными условиями;

— геометрия объекта и внешняя среда, которая определяет граничные условия.

К явлениям, приводящим к излучению АЭ волн, относятся три процесса:

— динамические локальные перестройки на поверхности и внутри структуры твердого тела, вызванные внешним воздействием на объект исследований (классическая акустическая эмиссия);

— утечки жидких и газообразных сред через несплошности структуры твердых тел, связанные с турбулентными либо кавитационными явлениями в каналах (акустическое течеискание);

— трение поверхностей твердых тел, вызванное трибоскопическими явлениями на трущихся поверхностях (акустическое течеискание).

АЭ «является отражением множества элементарных событий в объеме исследуемого объекта, каждое из которых происходит в случайный момент времени». Полагая, что каждое событие приводит к появлению импульса (например, импульса механического напряжения), изменяющегося во времени по некоторому закону f (t), в общем случае результирующий процесс x (t) можно записать в виде:

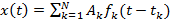                                                                                 (17.1)

где 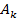— амплитуда импульса, появляющегося в момент времени 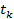; N — число зарегистрированных импульсов.

Исходя из этого, поток импульсов АЭ может быть представлен в виде случайной последовательности импульсов, у которых случайными являются амплитуда и время появления. Обычно форма импульсов определяется переходной характеристикой преобразователя, поэтому многие авторы считают, что функция f(t) одинакова для всех импульсов. Для большинства сигналов от источников АЭ характерна форма видеоимпульса.

Рассмотрим процесс разрушения твердого тела и сопровождающее его акустическое излучение. Для этого используем представление структуры твердого тела в виде плоской решетки (рис. 17.1). Считаем, что между атомами действуют силы связи, изображенные на рис. 17.1 в виде линий.

Трещина в виде разрыва связей распространяется слева направо. Сила F, приложенная к решетке твердого тела в вертикальном направлении, растягивает решетку, при этом в нагруженных продольных атомных связях накапливается упругая энергия.

При увеличении расстояния между атомами 2 и 3 до критического значения происходит разрыв межатомной связи 2–3, и атомы 2 и 3 начинаю динамически расходиться. Процесс сопровождается релаксацией связи 3–4 (в верхней части решетки) и симметричной ей связи в нижней части решетки. Релаксация в данном случае означает высвобождение энергии, накопленной предварительным растяжением, и соответствующее перемещение этих атомов вдоль цепочки.

Рис. 17.1. Схема развития разрушения атомной решетки

 

В результате релаксации возникает импульсное возмущение, отходящее от места разрыва в виде продольной L, поперечной Т волн и волны Рэлея S. Импульс продольной волны распространяется вдоль нагруженной связи; поперечной волны — в поперечном направлении вправо. Через определенное время импульсное возмущение достигает атомной связи 2–30 и создает дополнительное нагружение, которое при достаточной величине приведет к разрыву этой связи.

Распространение процесса разрушения происходит до встречи с препятствием (границы зерна, твердые включения) и сопровождается появлением свободной поверхности (поверхность разрушения) и процессом релаксации (выделением упругой энергии) из объема над поверхностью разрушения. При этом формируется поток элементарных импульсов, который образует акустическое смещение среды.

Разрывы связей в идеальной решетке распространяются вплоть до полного разделения тела на две части. Распространение фронта разрыва протекает, как уже говорилось, достаточно быстро. В идеальной структуре — со скоростью, близкой к скорости волны Рэлея (если не происходит ветвления трещины). На скорость распространения разрушения влияет также локальное напряженно-деформированное состояние материала. Расхождение берегов трещины, завершающее процесс разрушения, распространяется со скоростью поверхностной волны. Такое «быстрое» разрушение, при котором структура материала в областях, прилегающих к поверхности разрушения, не изменяется, считается хрупким разрушением. Разрушение материала в реальных условиях происходит, как правило, со скоростями на порядок и более медленными, чем при идеальном хрупком разрушении.

При нарушении структуры, появлении какого-либо препятствия на пути распространения фронта разрушения процесс разрыва связей приостанавливается и «хрупко» разрушается только некоторая часть тела, ограниченная неоднородностью структуры или поля напряжений. Проще всего представить прекращение процесса разрыва связей, полагая, что он заканчивается при подходе фронта разрушения к препятствию, например, к границам зерна.

Если рассматривать перемещение какой-либо точки на поверхности разрыва в результате релаксации атомных связей вблизи поверхности разрыва, то вначале происходит быстрое перемещение, а затем замедление перемещения и, наконец, полная остановка. В результате перемещение какой-либо точки на поверхности разрыва имеет временную форму ступенчатого импульса с фронтом, длительность и форма которого определяется величиной скачка трещины, скоростью распространения трещины, формы поверхности разрушения и местом начала разрушения.

Можно предложить выражение, которое аппроксимирует описанную зависимость в виде:

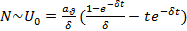                                                                             (17.2)

где N — число разорвавшихся связей, 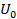 — перемещение вблизи поверхности разрыва,  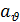— коэффициент, связанный со скоростью подъема функции, следовательно он связан с координационным числом решетки твердого тела 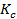, скоростью разрушения ϑ (т.е.  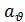= 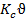) и местом начала разрушения, δ — параметр затухания, определяемый статистикой встречи фронтов разрушения с границами зерна.

Зависимость (97) есть не что иное, как выражение для функции источника, которая в сейсмоакустике определяется как временная функция скачка смещений на внутренней поверхности разрыва, а в предложенной выше модели — смещение точек поверхности образующейся трещины. Можно полагать, что это форма импульса АЭ непосредственно вблизи источника АЭ (в ближней зоне).

Характер смещений частиц среды в трехмерном теле, вызванных потоком элементарных импульсов от образовавшегося разрыва в дальней зоне источника представлен на рис. 17.2.

Форма импульса АЭ согласно приведенной кинематической модели в дальней зоне описывается эмпирическим выражением:

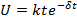                                                                                                         (17.3)

где k — коэффициент, связанный со скоростью разрушения; δ — параметр затухания.

Общий вид смещений среды, вызванный продвижением трещины, приведен на рис.17.3.

Рис. 17.2. Смещения частиц среды в трехмерном теле, вызванные потоком элементарных импульсов от образовавшегося разрыва вдали от источника

 

 

Рис. 17.3. Смещения частиц среды в трехмерном теле, вызванные потоком фрактонов

от образовавшегося разрыва (трещины) на различном расстоянии от источника:

а — вблизи источника; б — в переходной зоне; в — вдали от источника

Для рассмотренной вычислительной модели, основанной на кинематических процессах, получение формы импульса в дальней зоне производится путем расчета временной зависимости приращения величины площадки разрушения (которая совпадает с функцией источника). Таким образом, выбрав схему развития процесса разрыва атомных связей, в одном вычислительном эксперименте можно получить ряд интересующих нас величин. Среди них: зависимость величины приращения площадки разрушения, форма единичного импульса в дальней зоне, временная зависимость величины площадки разрушения, соответствующая функции источника, полный объем релаксации вблизи образовавшейся поверхности разрушения и связанное с ним смещение точек среды вблизи источника, т. е. смещение в ближней зоне.

В основу кинематической модели, описывающей процессы, происходящиев источнике АЭ при разрыве межатомных связей, положены следующие исходные моменты:

1. Начало разрушения имеет место в определенной области в некоторый начальный момент.

2. Начало разрушения, т. е. положение первой разорвавшейся связи, в однородном материале может быть в любой точке объема и определяется термофлуктуационными процессами в нагруженном твердом теле. Однако для реального материала, характеризующегося значительной неоднородностью, начало разрушения располагается вблизи какой-либо неоднородности, вероятнее всего, на границе зерна.

3. Фронт разрушения распространяется дискретными скачками конгруэнтно самому себе с некоторой скоростью. Форма фронта разрушения соответствует форме ячейки кристаллической структуры твердого тела. Наиболее вероятно, фронт мезоскопического акта разрушения трансформируется в окружность.

4. При каждом скачке фронта разрушения происходит разрыв некоторого числа межатомных связей и происходит релаксация атомных связей в объеме, расположенных над площадкой разрушения.

5. Фронт разрушения тормозится на некоторых границах, создающих «сильное» препятствие распространению разрушения. Как правило, скачок трещины или пластической деформации происходит на величину, определяемую однородным пространством внутри фрагмента (отдельности, зерна).

6. Смещение точек среды на поверхности разрыва и в непосредственной близости от нее является функцией источника АЭ и пропорционально увеличению размера площадки разрушения.

Описанная модель формирования единичного импульса АЭ при образовании и распространении трещины позволяет сделать ряд выводов, в том числе:

— крутизна переднего фронта единичного импульса АЭ определяется не только скоростью процесса разрушения, но и местом начала разрушения;

— в случае начала разрушения на границе площадки разрушения результирующий импульс будет иметь более пологий фронт, нежели в случае начала разрушения в центре площадки.

Приведенная схема протекания процессов разрушения межатомных связей позволяет определить численным расчетом временной ход нарастания процессов релаксации, изменения объема релаксации материала, ход изменения размера площадки разрушения. Полученные данные затем можно использовать для определения формы и параметров единичного импульса АЭ вдали от источника. Для этого можно использовать ход изменения объема релаксации или ход изменения размера площадки разрушения. В первом случае для получения формы импульса АЭ необходимо временную зависимость объема релаксации дважды продифференцировать по времени.

В случае использования временной зависимости изменения размера площадки разрушения, достаточно однократное дифференцирование полученной временной функции. В этом случае размер площадки разрушения можно интерпретировать как величину подвижки в сейсмологических терминах.

Если длительность скачка трещины 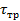 достаточно мала, то в дальней зоне можно принять импульсы продольной и поперечной волн раздельно. Условием для этого является:

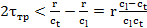                                                                                       (17.3)

где r — расстояние от источника до точки наблюдения; 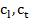— скорости продольной и поперечной волны соответственно.

Для скачка трещины порядка 1 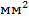 и расстояния от источника до приемника порядка 100 мм, это условие достаточно хорошо выполняется. Скачок трещины на 1  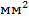совершается ориентировочно за время 0,1. . . 0,2 мкс. Правая часть условия (17.3) позволяет определить время раздельного приема импульсов продольной и поперечной волны, которое равно 15 мкс. Таким образом, во многих случаях, встречающихся на практике, продольные и поперечные волны, излученные источником, могут быть зарегистрированы раздельно.

Дальнюю зону источников АЭ можно оценить соотношением

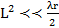                                                                                                             (17.4)

где λ — длина волны.

Это соответствует условию, чтобы разница длин векторов от точки наблюдения до двух максимально удаленных точек поверхности разрыва была существенно меньше четверти длины волны λ. Дальнюю зону можно еще определять как расстояние между источником и точкой наблюдения, которое соответствует расстоянию нескольких длин волн. В этом случае следует выбрать рассматриваемую длину волны (частоту).

Единичный импульс АЭ является сугубо индивидуальным сигналом, несущим информацию только о конкретной площадке разрушения и может быть получен, строго говоря, только расчетным путем. Значит, единичный импульс АЭ принципиально не может быть получен в аналитической детерминированной форме. Это связано со случайным характером процесса разрушения и соответствующей ему поверхности разрушения.

Ряд причин оправдывает получение аппроксимирующих зависимостей для представления аналитической записи единичного импульса АЭ. Среди этих причин:

— необходимость создания модели полного сигнала АЭ как стохастического импульсного процесса;

— постановка задачи создания оптимального приемника АЭ; — необходимость анализа прохождения сигналов через акустико-электронный тракт контролируемых объектов и систем АЭ контроля;

— необходимость создания систем классификации источников АЭ.

Во всех отмеченных проблемах, необходимо иметь аналитическое выражение для единичного импульса АЭ.

Рассмотренная модель формирования единичного импульса АЭ и аналитические выражения имеют ряд полезных применений:

— представляется возможность связать параметры импульса АЭ с параметрами процесса разрушений, например, величиной скачка трещины;

— модель позволяет объяснить ряд характерных особенностей формы единичного импульса АЭ, ранее не поддававшихся объяснению;

— появляется возможность для создания модели полного сигнала АЭ как случайного импульсного процесса;

— представляется возможность для постановки задачи создания оптимального приемника АЭ сигналов;

— получаем возможность для проведения анализа акустического и электроакустического тракта объектов и АЭ систем;

— имеем базу для создания системы классификации источников АЭ и составления критериев оценки состояния объектов.

Используя электроакустические аналогии, можно рассматривать источник АЭ как генератор ступенчатого напряжения (или тока) S(t), а среду как электрическую нагрузку. Для сферического АЭ источника в твердом теле эквивалентная нагрузка представляется соединением эквивалентных активного и реактивного (емкостного) сопротивлений.

Эквивалентную электрическую схему, позволяющую определить форму акустического сигнала при разрыве материала, можно представить в виде, показанном на рис. 17.4. Изменение механического напряжения в данном случае можно рассматривать с использованием эквивалентной схемы разряда емкости на активное сопротивление. Причем значения этих параметров, а следовательно, и постоянная времени данной эквивалентной цепи определяются размером зоны излучения и акустическими свойствами среды.

 

Рис. 17.4. Эквивалентная электрическая схема источника АЭ релаксационного типа:

Rи — импеданс источника, источник напряжения (механическое устройство);

С — емкость (упругость среды); R — активное сопротивление в момент разрыва связей; P — разрядник (закорачивающее устройство)

 

Эквивалентный акустический импеданс для источника АЭ большого размера относительно пространственной длительности импульса излучения и единичной площади имеет вид:

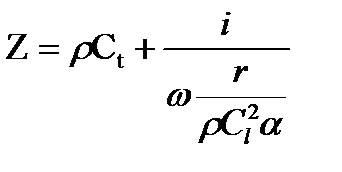                                                                                                 (17.5)

где α — безразмерная постоянная, близкая по значению единице; ρ — плотность среды; r — расстояние от источника АЭ до приемника.

Полный импеданс равен ZS (где S — площадь излучающей поверхности).

По структуре этого выражения можно считать, что

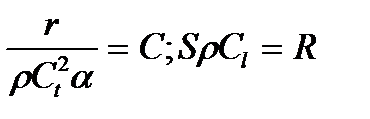                                                                                              (17.6)

Получили RC-цепочку, для которой постоянная времени разряда (заряда)

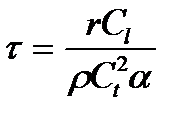                                                                                                            (17.7)

а время установления процесса .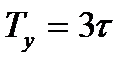

Рассмотрим теперь случай прорыва скопления дислокаций через препятствие. Вначале при возрастании напряжений происходит быстрый прорыв, после чего следует более медленный процесс распространения дислокаций. Этот процесс сопровождается релаксацией микронапряжений. Можно представить, что в момент прорыва дислокаций начинает действовать акустический источник вида ступенчатой функции S (t). Если рассматривать изменение напряжений в зоне головной дислокации, то там они упадут до нуля. Если рассматривать перемещения элементов тела, то вначале они равны нулю, а в конце процесса принимают определенные значения, характеризуемые статическим равновесием.

Однако в любом случае, рассматриваются изменения напряжений или изменения смещений (деформаций), в матрицу твердого тела излучается импульс упругой волны. Форма импульса определяется акустическими свойствами источника излучения и среды. Пространственная конфигурация источника излучения оказывает большое влияние на распределение излучения в пространстве (диаграмму излучения), чем на временную зависимость формы сигнала.

Таким образом, на микроскопическом уровне АЭ связана с процессами образования, движения и аннигиляции дефектов решетки твердого тела. Эти динамические процессы обусловлены разрывами межатомных связей или их восстановлением.

Пластическая деформация и вязкое разрушение сопровождается некогерентным акустическим излучением (непрерывная эмиссия), что аналогично в некотором роде белому свету с распределением энергии излучения по спектру, близкому к равномерному в некотором диапазоне волновых чисел.

Однако отдельные скачки пластической деформации и, соответственно, единичные импульсы АЭ можно также описать, используя схему формирования импульса АЭ. В случае скачка пластической деформации схема модели сохраняется такой же, как для трещины. Отличие заключается лишь в акустической модели элементарного источника АЭ.

В процессе скольжения дислокация, имеющая определенную длину (в направлении, нормальном плоскости рисунка), «заметает» некоторую площадь, при этом затрачивается определенная работа. При этом, также как и в случае скачкообразного роста трещины, высвобождается энергия. Схема сдвига одной части некоторого объема (кристалла) приведена на рис. 17.5.

Величину смещения верхней части кристалла относительно нижней можно оценить выражением:

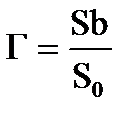                                                                                                                    (17.8)

где S — площадь скольжения; 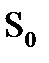— площадь сечения кристалла в плоскости скольжения; b — вектор Бюргерса.

Относительная деформация может быть выражена следующей формулой:

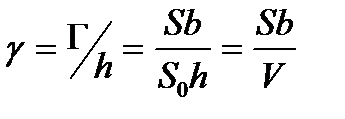                                                                                                (17.9)

где h — высота кристалла, V — объем кристалла/

Рис. 17.5. Сдвиг одной части кристалла относительно другой под действием сдвигового напряжения

 

Скачек пластической деформации моделируется двойной парой сил, тогда как скачек трещины отрыва моделируется сочетанием трех векторных диполей с отношением амплитуд 1 : 1 : (λ+2μ)/λ.

Скачки хрупкой трещины, вязкое разрушение и пластическая деформация — случайные импульсные процессы, первичными элементами которых являются единичные импульсы АЭ. Поэтому непрерывная АЭ не имеет принципиальных отличий от дискретной АЭ.

Они различаются только параметрами процесса и параметрами единичных импульсов. Самое важное отличие заключается в том, что, как правило, для пластической деформации имеет место поток элементарных импульсов АЭ, которые в результате особенностей регистрации, а также инерционности акустического и электроакустического канала перекрывают друг друга, образуя непрерывный стохастический процесс, который получил название непрерывной АЭ.

Лекция № 18. Акустическая эмиссия. Физические основы. Часть вторая

Элементарный источник сдвиговой деформации, моделирующий работу дислокационной петли, отличается от источника продольной деформации, связанной с образованием трещины отрыва, в основном типом излучаемых волн и диаграммой направленности излучения.

Отметим некоторые характерные особенности процессов, порождающих АЭ в твердом теле и возникающие при этом возможности. Анализ сигналов источников АЭ позволяет изучать параметры процессов возникновения, движения и аннигиляции дефектов кристаллической решетки в динамике, в реальном времени, а не по статически зафиксированным следам процессов, как это делается традиционно при исследовании микроструктур с использованием микроскопов.

Любая система стремится перейти из состояния с высоким значением потенциальной энергии в состояние с меньшим ее значением. Характер динамических процессов, происходящих в нагруженном твердом теле, носит окраскбифуркационно-релаксационных процессов. «Медленное» нагружение, когда скорость нагружения в материале объекта значительно меньше скорости звука, после преодоления потенциального барьера порождает быстрые процессы релаксации в твердом теле. Эти процессы сопровождаются излучением упругих колебаний.

При медленном нагружении в твердом теле постепенно возрастают механические напряжения, решетка твердого тела накапливает упругую потенциальную энергию. Поскольку в большинстве случаев нагружаемые объекты неоднородны по своим физико-механическим свойствам, в некоторой области твердого тела локальные напряжения достигают в определенный момент предельного значения и происходит разрыв внутренних связей кристаллической решетки. В этот момент быстро выделяется часть упругой энергии, накопленной ранее, определенная доля энергии расходуется на быстрое перемещение частиц в локальной зоне, где возникло нарушение связи. Происходит излучение упругой волны, а напряжения, сконцентрированные в зоне неоднородности, релаксируют.

Следует отметить, что при образовании или подрастании трещины импульсное воздействие на поверхности трещины при каждом ее скачке не приводит к излучению сигнала с длительными осцилляциями ввиду большой степени демпфирования излучающей поверхности (поверхности трещины). Поэтому наблюдаемые на практике сигналы АЭ осцилляторного (радиоимпульсного) типа возникают в результате многократных отражений в объекте импульсов АЭ.

При этом объект работает как некоторый резонатор, возбуждаемый видеоимпульсом. Осцилляции возможны также по причине сложной формы площадки разрушения, как было отмечено выше.

Возбуждение упругих волн в рассмотренных в данном разделе процессах возможно только в случае достижения критических значений действующих сил (независимо от их природы). Критические значения имеют место, когда сумма действующих сил достигает величины энергии разрыва межатомных связей. Неоднородностями твердого тела, которые могут служить источниками АЭ при нагружении, являются все типы дефектов кристаллической решетки.

Следовательно, условия, характерные для возникновения акустической эмиссии, в ряде случаев определяются медленным изменением и затем быстрым релаксационным изменением напряженно-деформированного состояния, во время которого излучаются упругие волны.

Таким образом, сигнал, сформированный в результате ускоренного движения, можно назвать акселерационным или сигналом а-типа, тогда как сигнал, возникающий в результате внезапного разрыва материала, можно назвать релаксационным или сигналом р-типа.

К сигналам а-типа относится также сигнал, возникающий в результате образования микротрещины в голове скопления дислокаций. Согласно условию образования микротрещины две головные дислокации должны сблизится на расстояние порядка величины вектора Бюргерса дислокации. Началу слияния первых дислокаций могут помочь термические флуктуации, после чего при достаточно большом напряжении все дислокации в скоплении вольются в микротрещину. Установлено, что при уровне напряжения 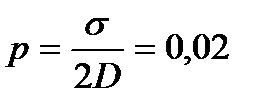(где D = G/2π(1−μ), G — модуль сдвига, μ — коэффициент Пуассона) после слияния уже с первых двух головных дислокаций остальные ускоренно сольются с образовавшейся микротрещиной. При этом форма излучаемого упругого импульса должна быть аналогичной форме импульса при аннигиляции дислокаций.

На основании рассмотрения ряда моделей источников АЭ можно прийти к выводу, что основной формой сигнала АЭ является видиоимпульс. В зависимости от типа источника сигнал АЭ может быть релаксационного или акселерационного типа (рис. 18.1).

 

Рис. 18.1 Основные типы одиночных сигналов АЭ:

а — релаксационный; б — акселерационный

Релаксационный сигнал можно описать выражением:

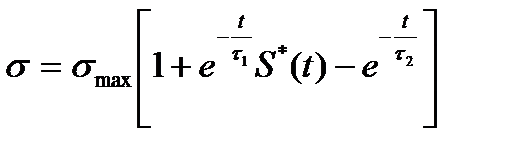                                                                                 (18.1)

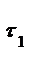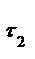где  и  — постоянные времени, зависящие от акустических свойств, в которой возник источник;  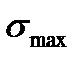— максимальные напряжения в момент разрыва связей.

Сигнал акселерационного типа описывается выражением

                                                                                                                                 (18.2)

 

где a — множитель, обеспечивающий необходимую размерность; k — коэффициент, определяемый физическим процессом, при излучении упругих волн k > 1.

Для рассмотренного случая аннигиляции скопления дислокации

                                                                                                                                 (18.3)

 

В качестве модели источника АЭ используют динамически расширяющуюся полость в твердом теле, тем самым полагая, что микроразрывы в материале имеют вид сферической полости, на поверхности которой нормальные напряжения падают от значения прозрачности материала до нуля.

В частном случае, когда 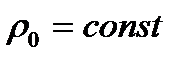(поверхностная нагрузка сферы) и область 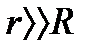, смещение частиц в излученной волне определяется из выражения   (18.4)

где 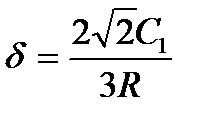; μ — коэффициент Пуассона; R — радиус сферы; r — расстояние от точки наблюдения; E — модуль упругости; 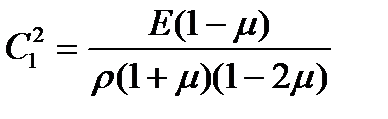; ρ — плотность материала.

Указанная модель может быть использована в ряде случаев при анализе процессов АЭ. Форма сигнала для данной модели приведена на рис. 18.2, из которого видно, что основная энергия сосредоточена в первой полуволне.

Если принять амплитуду первой полуволны за единицу, то амплитуда второй полуволны составит 0,12, третьей — 0,01.

Сферическая модель источника АЭ позволяет по параметрам принятого сигнала оценивать параметры сферической полости, которую в данном случае принимают эквивалентом источника АЭ. Так, длительность импульса определяется аргументом синуса, который включает радиус эквивалентной сферы и скорость продольных звуковых волн. Таким образом, измерив длительность импульса, можно оценить размер эквивалентной сферы.

Более близки к реальным источникам АЭ модели трещин, где проведен численный анализ модели трещины, образующейся в тонкой пластине, материал которой находится в состоянии плоского напряжения. Трещина, сквозная на всю толщину пластины, образуется в виде мгновенного разрыва материала. Решение получено для двух видов трещин: на краю пластины и в ее центре.

Численное решение несколько затрудняет общий анализ излучения трещиной упругих колебаний, однако с его помощью получены некоторые представления о процессе формирования сигнала АЭ и движения поверхностей трещины. На начальном этапе раскрытия трещины скорость расхождения ее поверхностей постоянна. В дальнейшем поверхности трещины совершают затухающие колебательные движения около положения равновесия. Характер движения подобен движению в сферической модели. На рис. 18.3 приведены рассчитанные значения перемещения некоторой точки на поверхности пластины при возникновении центральной трещины в функции времени.

 

Рис. 18.2. Форма акустического сигнала σ1 при воздействии на поверхность сферической полости ступенчатого импульса нагрузки: ϕ — аргумент синуса в выражении (18.4)

 

 

 

Рис. 18.3. Перемещение точки на поверхности пластины при возникновении

центральной сквозной трещины: 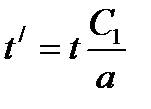 ; a — половина стороны пластины;  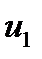— смещение частиц пластины в плоскости ее поверхности;  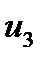— смещение, нормальное поверхности пластины

Выше рассмотрены модели одиночных источников АЭ. Для импульсов АЭ, излучаемых рассмотренными моделями, можно отметить общие признаки. Во-первых, все импульсы АЭ преимущественно однополярны, если пренебречь небольшими колебаниями на заднем фронте импульса. Однополярность свидетельствует о том, что спектр импульса АЭ достаточно широк и не имеет подчеркнутых частот, причем ширина спектра определяется длительностью импульса. Максимум спектральной плотности расположен на низких частотах или на постоянном смещении, и далее спектр монотонно уменьшается до нуля. Эти качественные признаки сигналов АЭ характерны для области излучения вблизи источника АЭ. Вдали от источника они могут изменяться.

По форме импульсы АЭ можно разделить на два вида — релаксационный и акселерационный. Формы сигналов АЭ, полученные в результате анализа сферического источника АЭ и источника в виде трещины нормального отрыва, близки к форме сигналов релаксационного вида.

Полный сигнал АЭ представляет собой совокупность элементарных сигналов. В зависимости от того, какой физический механизм деформации (разрушения) преобладает, полный сигнал может быть стохастической последовательностью импульсов p-типа (рис. 18.4, а), а-типа (рис. 18.4, б) или смешанной последовательностью (рис. 18.4, в). Задаваясь распределением параметров 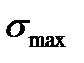, , 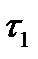, 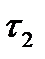k, временным промежутком между импульсами, полярностью импульсов или определив их значение, можно проводить анализ прохождения сигналов через акустико-электронный канал, включающий исследуемый объект и аппаратуру приема и обработки сигналов АЭ.

Параметры АЭ, являющейся стохастическим импульсным процессом, определяются актами срабатывания единичных источников и распределением этих источников в теле объекта.

Единичный источник АЭ при однократном срабатывании излучает импульс а-типа или p-типа. Основными параметрами этого импульса являются его амплитуда, длительность, длительности переднего и заднего фронтов, частотный спектр. Амплитуда и энергия импульса АЭ отображает энергетику единичного акта АЭ. Чем выше значения этих параметров, тем больше единичный скачек трещины или больше объем пластически деформирующего материала. В любом случае это свидетельствует о более интенсивном развитии повреждения материала объекта.

Длительность импульса АЭ также определяет энергию динамического процесса и объем материала, захваченного этим процессом. Длительности фронтов импульсов АЭ а- и p-типов непосредственно определяют длительность самого импульса и, следовательно, отображают ту же информацию.

Частотный спектр одиночного сигнала АЭ полностью определяется формой сигналов АЭ и не несет какой-либо дополнительной информации.

Рис. 18.4. Последовательности импульсов АЭ

Спектр последовательности импульсов АЭ имеет такой же вид, как и для одиночного импульса, составленного из отрезков экспоненциальных кривых.

Следовательно, анализ амплитудно-частотного спектра сигналов АЭ не может обеспечивать исходные данные для выбора частотного диапазона аппаратуры.

Диапазон АЭ аппаратуры и полоса пропускания в первую очередь определяются шумовыми условиями, в которых происходит контроль.

Одиночный импульс АЭ, распространяясь по элементам конструкции и проходя через преобразователь АЭ и избирательные электронные цепи, принимает вид затухающего радиоимпульса (рис. 18.5).

 

Рис. 18.5. Трансформация первичных импульсов АЭ после прохождения акустико-

эмиссионного канала:

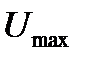 — амплитуда;  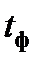— длительность переднего фронта;  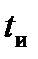— длительность импульса;  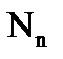— число осцилляций

Аппаратура АЭ регистрирует число событий, равное числу первичных сигналов АЭ, или число осцилляций (выбросов), равное числу пересечений сигналом АЭ порогового уровня Uп. Число выбросов определяется амплитудой и энергией первичного сигнала и, следовательно, по числу выбросов можно косвенно судить об энергетических характеристиках источника АЭ. Правильность регистрации числа событий АЭ и выбросов зависит от условий распространения сигналов АЭ и разрешающей способности аппаратуры. Как видно на рис. 18.5, число событий АЭ равно 5, а раздельно регистрируется аппаратурой только 4, первые два импульса из-за почти одновременного их прихода на датчик регистрируются как одно событие.

Непрерывная АЭ является последовательностью перекрывающихся импульсов АЭ. Принципиальная трудность в различении двух импульсов АЭ возникает в случае одновременного или почти одновременного прихода импульсов АЭ от разных источников на датчик. В других случаях превращение последовательности импульсов АЭ в непрерывную АЭ обусловлено частотными ограничениями канала передачи: объект–датчик–прибор, или, другими словами, его разрешающей способностью.

Число событий (импульсов) АЭ и связанное с ним число выбросов является одним из наиболее важных и легко регистрируемых параметров АЭ. В ряде случаев можно найти закономерную связь между числом зарегистрированных сигналов и такими параметрами, как длина трещины или ее площадь.

Подсчитывая число сигналов, можно судить об увеличении длины дефекта и его площади.

Важным параметром является также активность АЭ или частота следования импульсов АЭ. Число импульсов АЭ в единицу времени свидетельствует о скорости развития повреждения. Моменты времени прихода сигналов АЭ на датчики важны при определении координат источника сигналов.

Все перечисленные параметры сигналов АЭ являются случайными величинами и полная их характеристика задается только законами распределения этих величин.

Модель процесса АЭ можно представить в виде

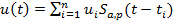                                                                                 (18.5)

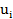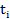Где  и - амплитуды импульсов АЭ и момент их появления — статистически независимые случайные параметры;  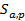— характеристика формы единичного импульса.

Среднее значение или математическое ожидание АЭ как случайного процесса можно записать

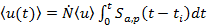                                                                        (18.6)

Где 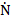 - активность АЭ или среднее число импульсов в единицу времени;  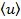— эффективное значение АЭ.

Если считать, что импульсы АЭ распределены во времени по закону Пуассона, то функция корреляции АЭ имеет вид

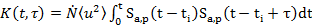                                             (18.7)

В этих выражениях 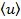 и 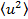 означает статистическое усреднение по амплитуде.

Лекция № 19. Акустическая эмиссия. Обобщенная модель полного сигнала акустической эмиссии. Часть первая

Структура твердого тела представляет собой набор случайно ориентированных зерен. Разрушение тела происходит путем последовательного разрушения зерен. Каждому когерентному разрушению отдельного зерна соответствует излучение единичного импульса АЭ, параметры которого индивидуально соответствуют форме и размеру разрушившегося зерна. В общий сигнал АЭ вносит вклад каждый элементарный источник, поэтому, учитывая выражение (17.3), выражение для сигнала АЭ, сопровождающего разрушение материала, можно записать в виде:

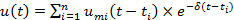                                                                 (19.1)

где 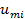— амплитуда i -го импульса.

Следует заметить, что переходная характеристика преобразователя АЭ и последующего тракта усиления вносят свои коррективы в общий вид сигнала АЭ. Сигналы АЭ (см. рис. 18.1) на выходе усилительного тракта приобретают осцилляторную форму (рис. 19.1)

Форму электрического импульса, т. е. импульса на выходе ПАЭ можно аппроксимировать выражением:

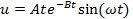                                                                                           (19.2)

где A — амплитудный коэффициент, размерность которого должна быть [В/с].

Численное значение его может выбираться при выполнении калибровки; B —параметр затухания осцилляций, связанный с потерями в преобразователе.

Для принятой формы импульса (19.2) момент достижения максимума колебаний можно определить, продифференцировав и приравняв нулю коэффициент при синусе выражения (19.2). Оказывается, что момент достижения максимума колебаний связан с параметром затухания В и может быть определен выражением:

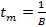                                                                                                                (19.3)

 

Рис. 19.1. Общий вид сигнала АЭ на выходе усилительного тракта аппаратуры

Величина максимума после подстановки 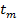 в (114) с учетом, что максимум положительной полуволны имеет место при  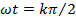(где k — нечетное целое число), равна:

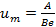                                                                                                              (19.4)

где e — основание натуральных логарифмов. В дальнейшем при анализе зависимости энергии сигнала АЭ и энергетических параметров от амплитуды сигнала АЭ изменение 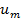 будет задаваться изменением численного значения амплитудного коэффициента А.

В большинстве случаев для резонансных ПАЭ, используемых в практике АЭ контроля промышленных изделий, характерно достижение сигналом максимума положительной полуволны при фазе сигнала 5π/2, тогда из условия 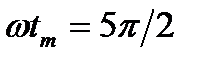, получим соотношения: B = 0,8f = 0,8T. В этом случае при любом изменении амплитуды механического импульса, поступающего на ПАЭ, электрический импульс достигает своего максимального значения через 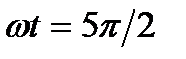, т. е. на третьем положительном полупериоде.

Параметры АЭ сигнала, которые непосредственно можно измерить, зарегистрировав сигнал, например, на экране запоминающего осциллографа называются первичными параметрами. К ним относятся: максимальное значение сигнала 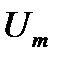; время нарастания  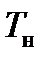— это время с момента пересечения сигналом порога дискриминации  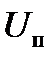до времени достижения сигналом максимальной амплитуды; длительность спада  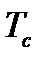— время с момента достижения максимальной амплитуды до времени ухода сигнала за порог дискриминации амплитуды; время начала сигнала АЭ  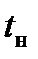— время с момента начала измерения до пересечения сигналом порога дискриминации; время окончания сигнала АЭ  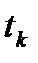— время с момента начала измерения до времени ухода сигнала за порог дискриминации амплитуды; длительность импульса .

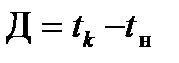Максимальное значение АЭ сигнала или его амплитуда измеряется в абсолютных величинах, микровольтах, либо в относительных, децибелах. Связь амплитуды сигнала, выраженного в микровольтах, с амплитудой, выраженной в децибелах, определяется формулой

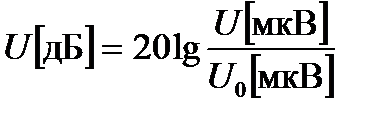                                                                                            (19.5)

где принято значения амплитуды сигнала относить к 1 мкВ, т.е.,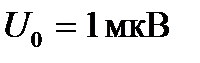

Вторичными параметрами считают те, которые можно определить расчетным путем, пользуясь формой единичного импульса и значением его параметров. К таким параметрам относятся: энергия E, площадь под огибающей сигнала, спектр сигнала и др.

Один из важнейших параметров АЭ процесса, а именно, энергия, в настоящее время не измеряется, а вычисляется. Это связано с тем, что отсутствуют относительно простые технические средства (преобразователи) и методики, позволяющие производить непосредственные измерения энергии акустического сигнала в твердом теле.

При вычислении энергии АЭ импульса различных «энергетических параметров» (квазиэнергии) используют такие характеристики и параметры АЭ сигнала, как амплитуда, временная зависимость мгновенного значения сигнала, временная зависимость огибающей электрического АЭ импульса на выходе преобразователя АЭ и др. Для расчета энергии АЭ необходимо задаться формой АЭ импульса в механическом (акустическом) и электрическом (на выходе преобразователя АЭ) виде.

Энергия любого сигнала определяется с использованием выражения:

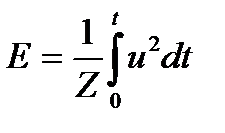                                                                                                            (19.6)

где u — мгновенное значение сигнала (электрического сигнала АЭ в нашем случае), Z – электрический импеданс (сопротивление) элемента электрической цепи, в которой оценивается энергия сигнала (здесь это электрический импеданс ПАЭ с учетом входной цепи прибора).

Подставим в (19.6) выражение для АЭ импульса (19.2), получим:

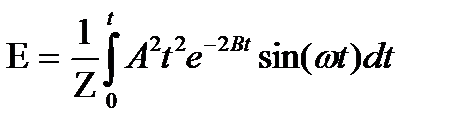                                                                                  (19.7)

и, выполнив интегрирование, получим:

      (19.8)

Выражение (19.8) для энергии Е представляет собой функцию, аргументами которой является время — t, амплитуда сигнала — 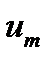 (выраженная через амплитудный коэффициент A) и параметры — A, ω, Z, т. е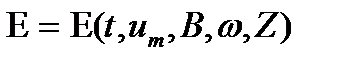

Для вычисления значений энергии и расчета зависимости энергии от амплитуды сигнала необходимо подставить пределы интегрирования по времени.

Одним из пределов является значение t = 0, а другой предел следует выбирать из значений 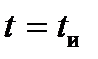 (  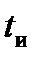— длительность импульса АЭ), либо t → ∞.

Следует отметить, что длительность импульса определяется промежутком времени между пересечениями передним и задним фронтами импульса выбранного порога, задаваемого значением порогового напряжения — 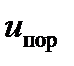 (или 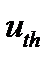). Начало импульса — пересечение порога передним фронтом, окончание импульса — пересечение порога задним фронтом (на спаде импульса). Подставляя в (19.8) указанные значения t, получим: для пределов интегрирования [0, ]

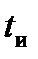                                                                                                                                 (19.9)

 

для пределов интегрирования [0, ∞]

                                                                                                                               (19.10)

 

Если 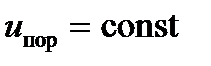 и равно фиксированному значению порогового напряжения, то пороговое время  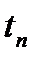изменяется в зависимости от  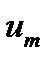в соответствии с выражением:

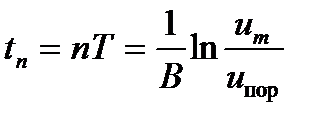                                                                                                (19.11)

Здесь 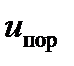 — пороговое напряжение, которое определяет измеряемую часть сигнала в пределах 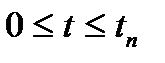,  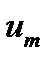— амплитуда импульса. Соотношение (19.11) получено из выражения 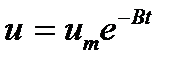, представляющего собой часть выражения (19.2), в котором опущена синусоида и вместо  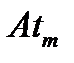записано 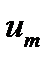. Если за начало координат взять момент t = 0, то 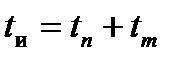. Поэтому, используя  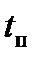вместо 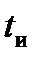, следует помнить, что вносится небольшая ошибка, что приемлемо, поскольку это значительно упрощает выкладки, а ошибка не превышает 5 %. Кроме того, в (19.8) и (19.9) учтено, что .

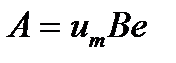В выражении (19.9) зависимость энергии от амплитуды более «сильная»,чем квадратичная, поскольку имеются логарифмические члены, содержащие амплитуду. Это объясняется тем, что при постоянном пороге при увеличении амплитуды сигнала одновременно увеличивается и длительность импульса, поскольку момент пересечения сигналом порога (измеряемая часть сигнала) удаляется от начала импульса. Увеличивается длительность измеряемой части сигнала и добавляется энергия. Однако численные оценки показали, что вклад логарифмических частей в выражении (19.9) незначителен и им можно пренебречь.

Если аппаратура АЭ построена таким образом, что измерения энергии производятся при выполнении условия 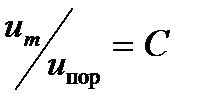С, где С можно выбирать, например, равным 0,1, тогда сохраняется постоянство таких величин, как n и 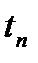. В этом случае энергия импульса АЭ не зависит от длительности.

Из проведенных рассуждений видно, что результат расчета E зависит от построения аппаратуры, что необходимо учитывать при анализе результатов АЭ контроля.

Ряд разработчиков аппаратуры АЭ полагает, что расчет энергии сигнала АЭ в реальном времени относительно сложен (он включает возведение мгновенных значений сигнала в квадрат и интегрирование полученной функции).

Поэтому иногда для упрощения используют квазиэнергетические параметры, расчет которых более прост. В США, например, достаточно широко используют параметр MARSE (Measured Area under Rectifaied Signal Envelope), представляющий собой интеграл от огибающей сигнала. Если аппроксимировать огибающую 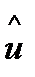 выражением

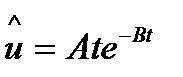                                                                                                          (19.12)

то параметр MARSE можно рассчитать следующим образом:

 

                                                                                                                               (19.13)

Для пределов интеграла [0, ∞] имеем:

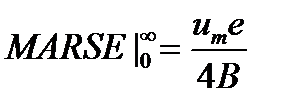                                                                                                   (19.14)

Обращаем внимание на линейную зависимость MARSE от .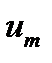

Для пределов интеграла [0, 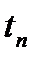] с учетом (123) имеем:

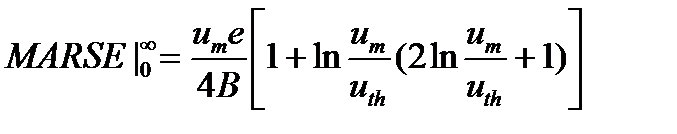                                                               (19.15)

где .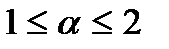

Если принять 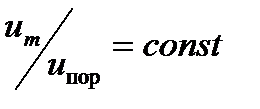 (порог, привязанный к 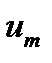), то

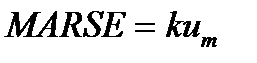                                                                                                       (19.16)

где k — константа, MARSE сохраняет в этом случае линейную зависимость от 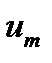 также, как и для случая выражения (19.6). Изменяется только численное значение коэффициента при .

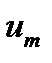Отсюда видно, что при конструировании аппаратуры и выборе методики измерения MARSE важно учитывать рассмотренные выше обстоятельства. В зависимости от разных подходов может изменяться не только значение констант, которые можно учесть при калибровке, но и вид зависимости энергии от амплитуды сигнала.

Простейшей моделью таких процессов является прямоугольный импульс (рис. 19.2). Его можно записать в виде

                                                                                                                               (19.17)

 

Прямоугольный импульс, длительность которого стремиться к нулю ΔT →0, а высота определяется соотношением

                                                     ΔT h = 1                                                       (19.18)

называется δ-импульсом.

Спектральная плотность прямоугольного импульса имеет вид

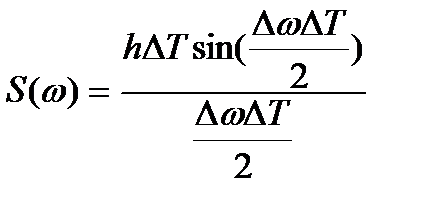                                                                                       (19.19)

 

Рис. 19.2. Прямоугольный импульс

 

Рис. 19.3. Амплитудный спектр прямоугольного импульса

Амплитудный спектр такого сигнала |S (ω)| будет иметь вид, представленный на рис. 19.3. Основная доля энергии сигнала сосредоточена в части спектра до первого пересечения функции |S (ω)| с осью абсцисс. Первый «нуль» функции S(ω) образуется при равенстве

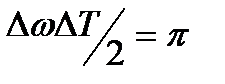                                                                                                          (19.20)

Отсюда получим

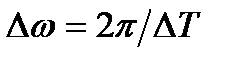                                                                                                         (19.21)

Анализируя это выражение можно сделать следующий вывод: ширина полосы спектра сигнала обратно пропорциональна его длительности. Так как длительность δ-импульса стремиться к нулю (ΔT →0), то в спектре δ-сигнала присутствуют частоты от 0 до ∞. Знание спектра АЭ необходимо для решения одной из важнейших проблем АЭ технологии — предохранения от шумов.

Огромный прогресс наблюдается с тех пор, когда в начале 1970-х для избежания помех от уличного транспорта и работающего в дневное время технологического оборудования, АЭ эксперименты проводились по ночам в подземных лабораториях на малошумящих испытательных машинах. Использование современных технологий АЭ контроля сегодня позволяет проводить измерения также и на шумных объектах. Первый шаг АЭ контроля заключается в выборе подходящего частотного диапазона тестирования. Акустический фоновый шум, как известно, является более высоким на низких частотах. Практически для 90% испытаний подходящий частотный диапазон заключен между 100 и 300 кГц. В шумящей среде (например, на электрических силовых станциях) для снижения шумов, исходящих от потоков жидкости, необходимо работать на более высоких частотах, в районе 500 кГц. Вследствие того, что использование высоких частот приводит к снижению диапазона обнаружения (расстояние между приемными датчиками уменьшается), между частотным диапазоном и ограничением шумов существует взаимооднозначная связь. К источникам акустических шумов относятся потоки жидкости в насосах и задвижках; процессы трения, например, трение конструкций в местах опор; процессы, связанные с ударами, например, капли дождя или биение кабеля о конструкцию под воздействием порывов ветра. К источникам электрических и электромагнитных шумов можно отнести земляные контуры, включенные силовые цепи, радио и навигационные передатчики, а также электрические штормы. Существуют различные пути решения проблемы снижения шумов. Во-первых, иногда шум можно снизить или даже прервать непосредственно в источнике. Во-вторых, воздействие акустического шума можно ограничить путем создания демпфирующих барьеров в стратегических точках конструкций. Проблема снижения электрических шумов, которая возникает в основном в связи с недостаточным заземлением и экранированием, решается при помощи использования правильных технологий, например, за счет применения дифференциальных датчиков или совмещенных датчиков со встроенными предусилителями. Если использование таких датчиков не позволяет окончательно решить данную проблему, ее приходится решать уже на программном и/или аппаратном уровне. Для получения удовлетворительной чувствительности часто используется технология плавающего порога, которая является весьма эффективной при условии, что не происходит существенной потери АЭ данных. Развиваются методы выборочного отбора и записи данных, базирующиеся на факторах времени, нагрузки или местоположения в пространстве. Кроме того, в связи с тем, что источники шумов по характеристикам формы сигналов отличаются от настоящей эмиссии, связанной с дефектами, их отделяют путем реализации и использования математических методов дискриминации на компьютере. Такую машинную обработку можно проводить и сразу же после измерения, и во время процесса отображения информации (графического фильтрования), и уже после испытаний в процессе послетестовой обработки, используя программы послетестовой фильтрации или специального пакета, предназначенного для анализа формы сигналов. Благодаря развитию и использованию этих методик, АЭ контроль внедрился в разнообразные сферы производства и в дальнейшем можно ожидать продолжение этого. В качестве примеров приложений, в которых снижение шума являлось ключом к успешному использованию АЭ контроля, можно назвать мониторинг в процессе сварки и обнаружение усталостных растущих трещин в конструкции летящего самолета.

Длительность механических шумов, сопутствующих проведению АЭ контроля производственных объектов, существенно больше длительности процессов образования и роста дефектов, поэтому они характеризуются узким частотным диапазоном, расположенным в низкочастотной части спектра. Частотный спектр механических шумов не превышает 200 кГц (рис. 19.4).

Выбор рабочей частоты АЭ контроля следует проводить из компромисса между приемлемым расстоянием между преобразователями и шумовой обстановкой объекта контроля. Как известно, затухание ультразвуковых волн возрастает с увеличением частоты. Понятное стремление увеличить расстояние между АЭ преобразователями (увеличение зоны контроля) может быть реализовано выбором более низкой частоты АЭ контроля. С другой стороны сдвиг рабочей частоты в область низких частот влечет за собой увеличение влияния механических шумов, что значительно затрудняет выделение полезного сигнала из помех (см. рис. 19.4). Но увеличение рабочей частоты АЭ контроля уменьшает энергию полезного АЭ сигнала, т.к. основная часть энергии сигнала от дефекта лежит в области низких частот (см. рис. 19.4).

Для борьбы с механическими шумами применяют частотные фильтры, которые пропускают сигналы в определенном диапазоне частот. Нижняя граница фильтра (НГФ) выбирается таким образом, чтобы не пропустить сигналы от шумов, расположенных в низкочастотной части спектра (рис. 19.5).

Верхняя граница фильтра (ВГФ) выбирается для осуществления процесса оцифровки АЭ сигнала, т.к. частота оцифровки должна превышать в два раза частоту аналогового сигнала (согласно теоремы Котельникова), т.е.

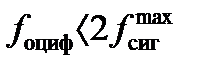                                                                                                           (19.22)

 

 

Рис. 19.4. Спектр АЭ сигнала и спектры сигналов от механических шумов:

1 —механический шум; 2 — полезный сигнал

 

 

Рис. 19.5. Частотная фильтрация:

1 — механический шум; 2 — полезный сигнал; 3 — пропускаемый частотный диапазон; 4 — фильтр

 

Лекция № 20. Акустическая эмиссия. Аппаратура акустико-эмиссионного контроля

Общие положения

Аппаратура АЭ контроля предназначена для приема, усиления, обработки и регистрации сигналов АЭ. Она содержит: преобразователи АЭ; предварительные усилители и основные усилители; средства идентификации и обработки сигналов, включая пороговые устройства, устройства выделения и измерения параметров сигналов АЭ, устройства регистрации и представления информации (блоки обработки сигналов АЭ); контроллеры. Совокупность элементов: преобразователь АЭ → кабель, соединяющий преобразователь АЭ с предусилителем → предусилитель → кабель, соединяющий предусилитель с основным блоком → основной усилитель → блоки предварительной обработки АЭ-сигнала — образуют электрическую часть АЭ канала. При лабораторных исследованиях необходимо также наличие средств обеспечения эксперимента — систем нагрева, поддержания и измерения вакуума, нагружающих устройств и т.п.

Технические данные, характеризующие работу аппаратуры АЭ, подразделяются на основные и общие. К основным параметрам и техническим характеристикам аппаратуры АЭ относятся: уровень собственных шумов усилительного тракта 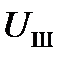; амплитудный динамический диапазон; амплитудно-частотная характеристика (АЧХ); диапазон рабочих частот; максимальная скорость обработки импульсов АЭ; число каналов аппаратуры; перечень измеряемых параметров сигнала АЭ; перечень устанавливаемых параметров аппаратуры АЭ.

К устанавливаемым параметрам относятся: интервал контроля пика (ИКП (Rise time)), интервал контроля длительности (ИКД (SCETO)), интервал контроля конца импульса (ИКК (Dead time)) (рис. 20.1).

Рис. 20.1 Устанавливаемые временные параметры

Интервал контроля пика определяет зону регистрации максимальной амплитуды события. Началу интервала контроля пика присваивается время первого пересечения осцилляциями порога дискриминации. Далее происходит сравнение амплитуды осцилляции, за которой «закреплено» начало интервала контроля пика с амплитудой следующей осцилляции. Если амплитуда следующей осцилляции превышает амплитуду предыдущей, то начало интервала контроля пика присваивается времени пересечения осцилляции с большей амплитудой.

Процесс повторяется до тех пор, пока в интервале контроля пика не окажутся осцилляции с большей амплитудой. Обычно интервал контроля пика устанавливают 200. . . 400 мкс. Интервал контроля длительности выделяет отдельные события среди осцилляций. Началу интервала контроля длительности присваивается время первого пересечения осцилляциями порога дискриминации.

Далее происходит проверка наличия пересечения следующей осцилляцией порога дискриминации амплитуды. Если осцилляция пересекает порог дискриминации, то началу интервала контроля длительности присваивается время пересечения этой осцилляции порога дискриминации. Процесс повторяется до тех пор, пока в интервале контроля длительности не окажутся осцилляции с амплитудой, меньшей порога дискриминации. Обычно интервал контроля длительности устанавливают 600. . . 800 мкс.

Интервал контроля конца импульса блокирует канал после конца импульса.

В это время канал запирается и не принимает сигналы. Интервал контроля конца импульса устанавливают около 1000 мкс.

Общими параметрами и техническими характеристиками являются: напряжение электрического питания; потребляемая мощность; климатические и технические условия работы аппаратуры; масса аппаратуры; габаритные размеры аппаратуры и отдельных блоков; число блоков аппаратуры.

По сложности аппаратуру АЭ контроля разделяют на приборы и системы.

Приборы, основанные на акустических методах контроля используются для диагностирования в различных областях:

— нефтегазовой и химической промышленности, трубопрокатных и метал лургических предприятиях;

— тепловой и атомной энергетике, авиационно-космической технике, в железнодорожном транспорте;

– подъемных сооружениях, мостовых конструкциях, бетонных и железобетонных сооружениях.

Их применяют для решения задач, связанных:

— с лабораторными исследованиями материалов;

— с технологическим контролем элементов конструкций;

— с эксплуатационным контролем.

С помощью этих приборов контролируют высоконагруженные и крупногабаритные объекты повышенной опасности, а также объектов, где ограничен доступ к поверхности контроля (некоторые виды трубопроводов, сосудов давления, котлов, резервуаров, агрегатов).

Системы АЭ являются многоканальными устройствами, представляющими собой совокупность аппаратных средств, вычислительных устройств и специализированного программного обеспечения и включающее как специализированные процессоры, так и универсальные ЭВМ.

Для регистрации акустической эмиссии при испытаниях крупномасштабных объектов следует применять приборы акустической эмиссии в виде многоканальных систем, позволяющих определять координаты источников сигналов и характеристики АЭ с одновременной регистрацией параметров нагружения (давления, температуры и т. д.). Многоканальная система акустической эмиссии должна включать: комплект предварительных усилителей; кабельные линии; блоки предварительной обработки и преобразования сигналов акустической эмиссии; ЭВМ с необходимым математическим обеспечением; средства отображения информации; блоки калибровки системы. АЭ система может быть как стационарной, так и передвижной.

Существует значительное количество разнообразных приборов и систем для регистрации информативных параметров АЭ. По мере развития представлений о природе АЭ создаются новые приборы. В настоящее время наряду с раннее разработанными приборами (специализированными, для комплексных исследований, для контроля крупногабаритных объектов) используются современные системы АЭ.

Приведем краткий обзор раннее созданных и современных приборов и систем АЭ.

Специализированные приборы предназначены для решения конкретных задач неразрушающего контроля. Приборы для комплексных исследований, предназначенные для приема сигналов, возникающих при развитии дефектов в образцах и реальных конструкциях, позволяют измерять различные параметры излучения и оценивать состояние контролируемого объекта. Они отличаются возможностью одновременно измерять и анализировать большое число параметров АЭ, разнообразием способов вывода информации. Приборы для контроля крупногабаритных объектов служат для оценки опасности появления и накопления дефектов, определения местоположения источников АЭ, в качестве систем контроля аварийных ситуаций ответственных сооружений. Обычно эти системы многоканальные.

Для целенаправленного использования этих приборов проведена их классификация. В общем случае их можно классифицировать по назначению, измеряемым параметрам, характеристикам измерительных каналов, способам регистрации информации, методам селекции сигналов.

Наряду с классификацией по назначению, приборы АЭ можно классифицировать по измеряемым параметрам, так как регистрировать все параметры

АЭ одним прибором сложно. В качестве базовых понятий АЭ приняты: суммарный счет, скорость счета, энергия сигнала, максимальное значение амплитуды импульса АЭ, мгновенное значение амплитуды импульса АЭ.

При классификации по характеристикам измерительного тракта, способам записи информации и самопроверки используются следующие характеристики:

— рабочий диапазон частот;

— чувствительность аппаратуры по входу преобразователей АЭ;

— коэффициент усиления;

— селекция помех различной физической природы;

— регистрация информации;

— контроль работоспособности.

Современные системы представляют собой принципиально новый уровень накопления и обработки АЭ информации. Системы машинной обработки АЭ информации оперируют не только со всеми стандартными параметрами метода

АЭ, но и рядом дополнительных параметров, таких как: длительность импульсов, энергия импульсов, распределение по амплитудам, энергиям, длительностям и рядом других специальных параметров. Общее число анализируемых параметров может достигать порядка двадцати наименований.

В последние годы в состав систем АЭ включается все большее количество вычислительных средств различных классов. При этом на компьютер возлагаются следующие задачи:

— параллельный прием и накопление многоканальной информации;

— расчет координат источника или зоны его нахождения;

— проверка истинности локационной серии;

— статистическая обработка АЭ информации;

— расчет спектров огибающей АЭ импульсов;

— графическое представление и документирование результатов;

— управление настройкой параметров аппаратуры;

— тестирование и контроль работоспособности системы;

— принятие решения с учетом дополнительной априорной информации.

Особенностью нового поколения АЭ систем является:

— большой динамический диапазон регистрации сигналов, который обеспечивается использованием прецизионных логарифмических усилителей, хорошей экранировкой и развязкой каналов;

— применение в измерительных каналах высокопроизводительных цифровых сигнальных процессоров для обработки и регистрации параметров сигналов АЭ;

— широкий выбор конфигураций систем, комплектация чувствительными преобразователями АЭ (интегральными, герметичными, взрывозащищенными, с режимом автотестирования) для контроля объектов.