Время: 2 часа (90 мин.)

8.1 Основные вопросы

- факторы достоверности исходных фактов;

- факторы ослабления, вносимые правилами;

- вычисляемые факторы достоверности;

- И/ИЛИ-графы;

- узлы типаИ;

- узлы типаИЛИ;

Текст лекции

Для понимания существа нестрогого вывода удобнее всего рассмотреть способ организации базы правил и принципы функционирования механизма выводов на конкретном примере некоторой ЭС.

В этих целях рассмотрим экспертную систему МYСIN, которая предназначена для решения задач медицинской диагностики инфекционных заболеваний.

Все множество продукций МYСIN можно представить в виде совокупности И/ИЛИ графов, в самых нижних узлах которых располагаются основные системные данные (исходные факты Ф_i), а в самых верхних – заключения (С_j), выводимые системой.

Каждое правило МYСIN может включать одно или несколько условий, соединенных связкой "И". Графически такое правило можно представить в виде дерева, приведенного на рис.10.

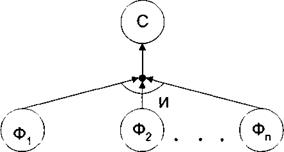
Рис.10. Графическое представление правила

В случае, когда имеется несколько правил, из которых выводится одно и то же заключение, используется связка "ИЛИ" (см. рис.11.).

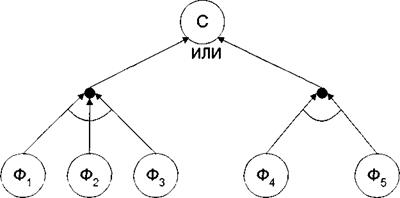
Рис.11. Графическое представление двух правил, из которых выводится одно заключение

Следует заметить, что в системе МYСIN все вершины ИЛИ являются бинарными, что достигается за счет искусственного сведения такого рода вершин произвольной арности к совокупности бинарных.

Система МYСIN функционирует в такой области, где решения редко принимаются наверняка. Поэтому разработчики этой системы объединили со стандартным механизмом выводов некоторую простую теорию правдоподобного рассуждения, позволяющую устанавливать для каждого заключения в И/ИЛИ дереве так называемый фактор уверенности (ФУ), варьируемый от 0 до 1. Согласно этой теории каждый факт, поставляемый пользователем системе, снабжается фактором достоверности (ФД), а каждое правило имеет свой фактор ослабления (ФО), вносимый в вывод и указывающий на "надежность", присущую той или иной продукции. Факторы достоверности и ослабления также принимают значения в диапазоне от 0 до 1.

На основе такого рода данных вычисляются факторы уверенности для каждого сделанного системой заключения. Осуществляется это с помощью двух следующих правил:

(1) – в вершинах типа "И" наименьший фактор
достоверности исходных данных умножается на фактор
ослабления, вносимый продукцией, и полученное значение
приписывается заключению в качестве его фактора
уверенности (благодаря этому заключение никогда не будет
иметь большую "силу", чем самое "слабое" из
поддерживающих его свидетельств-фактов). Формально это
выглядит следующим образом:

<ФУ заключения> = <min ФД исход. факта> х <ФО, вносимый правилом >;

(2) – в вершинах типа "ИЛИ" факторы уверенности,
вносимые правилами, подкрепляют друг друга и могут
обеспечивать большую "силу" заключению, чем каждое из
правил в отдельности. Вычисления осуществляются по
следующей формуле:

<Ф.У. заключения> = <Ф.У. заключения 1-го правила> + <Ф.У. заключения 2-го правила> - <Ф.У. заключения 1-го правила> х <Ф.У. заключения 2-го правила>.

Следует заметить, что если правдоподобность некоторого заключения, определяемая его фактором уверенности, падает ниже некоторого значения (в МYСIN оно равно 0,2), то оно отвергается и в процессе дальнейшего вывода не участвует. На рис.12. приводится пример И/ИЛИ дерева для вычисления фактора уверенности одного финального заключения-гипотезы.

Е=0,8        Е=0,2    Е=0,9    Е=0,7          

Е – факторы достоверности исходных фактов

А – факторы ослаблений, вносимые продукциями

С – вычисляемые факторы уверенности.

Рис.12. И/ИЛИ дерево для вычисления фактора уверенности заключения-гипотезы

На приведенном примере хорошо видна направленность вывода (снизу-вверх), соответствующая восходящему выводу.