ЛЕКЦИИ
по дисциплине 1423 Системы искусственного интеллекта
для студентов 5 курса факультета ИТ
специальности 230101
«Вычислительные машины, комплексы, системы и сети»
Обсуждены на заседании кафедры
«___» _______________ 2007 г.
Протокол № _____
Москва, 2007
Общие положения
1.1 Цели дисциплины
Целью дисциплины является изложение основ теории систем искусственного интеллекта
1.2 Рекомендуемая литература
1.2.1 Основная:
1) Миронов А.С. Системы искусственного интеллекта: Учебное пособие. – М.: МГУПИ, 2007. – 48с.
2) Костров Б.В. и др. Основы искусственного интеллекта. – М: «ДЕСС», «ТехБух», 2007. – 192с.
1.2.2 Дополнительная литература:
1) Башмаков А.И., Башмаков И.А. Интеллектуальные информационные технологии. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 304с.
2) Рассел С., Норвиг П. Искусственный интеллект: современный подход. – М.: «Вильямс», 2006. – 1408с.
3) Джарратано Д., Райли Г. Экспертные системы: принципы разработки и программирование. – М.: «Вильямс», 2007. – 1152с.
2 Л екция №1. Основные понятия и определения.
Время: 2 часа (90 мин.)
2.1 Основные вопросы
- основные понятия СИИ.
Текст лекции
Системы искусственного интеллекта (СИИ) могут быть определены как интеллектуальные компьютерные программы, использующие знания и процедуры логических выводов для решения задач. Основными видами СИИ являются вопросно-ответные и экспертные системы. Архитектура СИИ представлена на рис.1.
СИИ
База знаний
Входная информация
Механизм обраб. знаний
Выходная информация
Рис.1. Архитектура СИИ.
Входной информацией для СИИ являются различные вопросы или факты, вводимые пользователем. Механизм обработки знаний связывает входную информацию с информацией, хранящейся в базе знаний, и на этой основе осуществляет логический вывод целевых заключений, выдаваемых пользователю в качестве результатов работы системы.
Знаниями принято называть формализованную в соответствии с определенными структурными правилами информацию, которую СИИ могут использовать при выполнении логических выводов. Иными словами, обработка знаний на ЭВМ представляет собой обработку их содержимого с помощью правил преобразования, адекватных тому или иному классу предметных областей.
При создании СИИ наиболее важной и сложной проблемой является проблема формализации знаний о предметных областях. Эта проблема получила название проблемы представления и обработки знаний. Решение данной проблемы заключается в разработке систем представления знаний (СПЗ).
Под СПЗ понимаются средства, позволяющие описывать знания о тех или иных предметных областях, а также выводить новые знания на основе уже имеющихся. Основу СПЗ составляет модель представления знаний (МПЗ) и соответствующая ей модель вывода знаний (МВЗ). Важное место в СПЗ занимает язык представления знаний (ЯПЗ), выразительные возможности которого определяются лежащей в его основе МПЗ.
Различают логические и эвристические МПЗ. Логические МПЗ базируются на использовании исчисления предикатов. Знания здесь выражаются с помощью средств формальной системы. В отличие от логических эвристические МПЗ (семантические сети, сети фреймов, продукционные правила) имеют для этого разнообразный набор средств. В основе методологии формализации знаний лежит такая дисциплина, как формальная логика.
В основе логических моделей представления знаний лежит понятие формальной логической системы (теории). Для описания теории вводится множество её базовых элементов, называемых алфавитом теории. Определяются правила построения правильных предложений (формул) теории из базовых элементов. Часть правильно построенных формул объявляются аксиомами (априори истинными формулами). Задаются, также, правила вывода новых формул из других правильно построенных формул.
Данный подход лежит в основе организации многих дедуктивных СИИ. В соответствии с ним база знаний описывается в виде предложений и аксиом теории, а механизм выводов реализует построение новых предложений из имеющихся в базе знаний. На вход СИИ поступает описание задачи в виде предложения (теоремы), которое явно не представлено в базе знаний. Но если оно верно с позиций имеющихся знаний, то может быть выведено из содержимого базы знаний путем выполнения механизмом выводов правил вывода. Процесс работы механизма выводов называют доказательством теорем.
С практической и теоретической точек зрения наиболее важной формальной теорией является исчисление предикатов. В нем предложения расчленяются на субъекты и предикаты. Расчленение предложения на субъект и предикат реализуется путем его соотнесения с логической функцией одной переменной P(X), выражающей свойство субъекта и называемой одноместным (унарным) предикатом. Если же предложение выражает отношение между несколькими субъектами, то с ними связывают n-местную логическую функцию P(X1, X2,…,Xn), называемую n -местным ( n -арным) предикатом.
В исчислении предикатов используются различные правила вывода, основными из которых являются правило подстановки и правило отделения.
В соответствии с правилом подстановки в формулу, которая уже выведена, можно вместо некоторого высказывания подставить любое другое во все места вхождения заменяемого высказывания.
В соответствии с правилом отделения из истинности высказываний a и a®b выводится истинность высказывания b (правило modus ponens).
Модифицированное исчисление предикатов лежит, также, в основе систем логического программирования. Здесь используются специальные классы логических формул, называемые хорновскими дизьюнктами. В качестве метода логического вывода (доказательства) используется метод резолюций.
Наиболее известной реализацией, среди таких систем, является система программирования Турбо-Пролог. В логической программе, в общем случае, описываются множество объектов, их свойств и отношений между объектами, а также правила вычисления ответов на возможные запросы пользователей.
Текст лекции
Формальная логика занимается изучением форм и законов мышления. Одной из главных ее задач является описание правильных человеческих рассуждений. Особый интерес к логике возник с появлением ЭВМ, когда была поставлена задача, научить машину «рассуждать».
Основными формами мышления, изучаемыми в логике, являются: понятие, суждение и рассуждение.
Первая форма мышления – понятие. Понятие о предмете составляет совокупность признаков предмета. Всякое понятие обладает содержанием – совокупностью признаков, определяющих данное понятие и объемом – совокупностью объектов, входящих в данное понятие.
В соответствии с этим определяют интенсионал и экстенсионал понятия. Интенсионал – это совокупность признаков понятия, а экстенсионал – перечисление конкретных его представителей.
При определении понятий различают реальное и номинальное определения. Типичным способом реальных определений понятий является определение через ближайшее родовое (более общее) понятие и указание видового отличия.
При номинальном определении понятий речь идет о выборе имени для понятия, определяемого через перечисление видовых.
Связь между объемом и содержанием понятий выражается в законе обратного отношения: если два понятия сравнимы и содержание первого из них больше, чем содержание второго, то объем второго понятия больше объема первого понятия.
С этим законом связаны способы обобщения (т.е. перехода от понятий с меньшим объемом и большим содержанием к понятиям с большим объемом и меньшим содержанием) и ограничения (т.е. перехода от понятий с большим объемом и меньшим содержанием к понятиям с меньшим объемом и большим содержанием).
По объему понятия делятся на пустые (реально не существующие), еденичные и общие. По содержанию понятия делятся на положительные и отрицательные (присутствуют или нет определенные признаки в понятии), безотносительные и относительные, сравнимые и несравнимые.
Сравнимые понятия (т.е. имеющие общие признаки в содержании) бывают совместимыми, (объемы понятий имеют совпадающую часть) и несовместимыми. Выделяют три вида отношений совместимости: равнозначность, пересечение и подчинение объемов. Существуют и три вида отношений несовместимости: соподчинение, противоположность, противоречие.
Одной из основных операций над объемом и содержанием понятий является деление понятия (т.е. деление родового понятия на множество видовых понятий). При её выполнении различают делимое понятие, основание деления (признаки) и члены деления (множество понятий, видовых по отношению к исходному). Частным случаем деления является дихотомическое деление (т.е. деление на два класса с противоречивыми признаками). Практическое применение операции деления понятий связано с классификацией, целью которой является приведении знаний о предметной области в систему.
Вторая форма мышления – суждение. В суждениях содержится информация о предметах и отношениях между ними. Соответствие или не соответствие суждения реальности определяет его истинность или ложность. С грамматической точки зрения, суждение – это повествовательное предложение естественного языка (ЕЯ).
Суждение может содержать логический квантор, выражаемый в ЕЯ словами «все», «некоторые» и т.п.
По структуре суждения делятся на простые, выражаемые простыми предложениями ЕЯ и сложные, выражаемые сложными предложениями ЕЯ. Простое суждение состоит из субъекта S (логическое подлежащее, определяющее то, о чем идет речь), предиката P (логическое сказуемое, определяющее то, что утверждается или отрицается о субъекте), логической связки «есть» или «не есть», выражающей связь между субъектом и предикатом (в ЕЯ она может лишь подразумеваться) и, возможно, логического квантора.
Простые суждения делятся на атрибутивные, выражающие принадлежность или не принадлежность свойств объекту или классу объектов, суждения об отношениях, выражающие наличие или отсутствие отношений между объектами или классами объектов и суждения о существовании (экзистенциональные суждения), говорящие о существовании или не существовании объектов или классов объектов.
По качеству простые суждения делятся на утвердительные и отрицательные. С количественной стороны простые суждения делятся на еденичные (в них что-либо утверждается или отрицается об одном объекте), частные (в них что-либо утверждается или отрицается о части объектов некоторого класса), и общие (в них что-либо утверждается или отрицается обо всех объектах некоторого класса).
Еденичные утвердительные и отрицательные суждения имеют логические формы “S есть P” и “ S не есть P ”.
Частноутвердительные и частноотрицательные суждения имеют логические формы “Некоторый S есть P” и “Некоторый S не есть P”.
Общеутвердительные и общеотрицательные суждения имеют логические формы “Всякий S есть P” и “Всякий S не есть P”.
Различают сравнимые и несравнимые суждения. Сравнимые суждения имеют одни те же субъекты и предикаты, но различаются связкой или квантором. Несравнимые суждения имеют различные субъекты и предикаты.
Сложные суждения – это суждения, состоящие из нескольких простых суждений, связанных между собой различными логическими связками. Связки выступают важнейшими элементами сложных суждений, т.к. определяют их структуру. Основными видами сложных суждений являются соединительные, разделительные, условные суждения и суждения эквивалентности.
Соединительные суждения представляют собой связь двух и более простых суждений с помощью логической связки “И” и имеют логическую форму pÙqÙ…Ùr.
Разделительные суждения представляют собой связь двух и более простых суждений с помощью логической связки “ИЛИ” и имеют логическую форму pÚqÚ…Úr.
Условные суждения состоят из двух простых суждений, связанных связкой “ЕСЛИ, ТО” и имеют логическую форму p®q.
Суждения эквивалентности состоят из двух простых суждений, связанных связкой “ЕСЛИ И ТОЛЬКО ЕСЛИ, ТО” и имеют логическую форму p~q.
Третья форма мышления – рассуждение. Простейшей формой рассуждений являются умозаключения. Посредством умозаключений из одного или нескольких суждений (посылок) получают новое суждение (заключение). Переход от посылок к заключению называется логическим выводом. Возможность вывода заключения из посылок обеспечивается наличием логической связи между ними. Истинные с точки зрения логики выводы формируются путем применения корректных правил вывода.
Умозаключения обычно записываются в следующем виде (форме):
А1, А2, …,Аn ├ B,
где А1, А2, …,Аn – посылки; B – заключение; “├”– знак логического вывода. Допустима еще одна форма записи умозаключений в виде дроби:
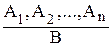
Логический вывод – это, в общем случае, многоэтапный процесс перехода от посылок к заключениям и далее от полученных заключений (как новых посылок) и исходных посылок к новым заключениям. Выполняется этот процесс в виде элементарных актов, каждый из которых есть шаг вывода, на котором применяется соответствующее правило вывода. Вывод за один шаг называется непосредственным выводом.
По характеру связи между знаниями, выраженными в посылках и заключениях, умозаключения классифицируются как:
– дедуктивные (от общего знания к частному знанию);
– индуктивные (от частного знания к общему знанию);
– традуктивные (от частного знания к частному знанию).
При выполнении дедуктивных умозаключений считается, что истинные посылки порождают только истинные заключения. В соответствии с характером посылок, которые могут быть простыми (простыми атрибутивными суждениями, называемыми также категорическими) или сложными суждениями различают простые и сложные дедуктивные умозаключения.
В зависимости от количества посылок дедуктивные умозаключения делятся на непосредственные, в которых заключение выводится из одной посылки, и опосредованные, в которых заключение выводится из двух посылок.
К непосредственным дедуктивным умозаключениям относятся такие умозаключения, как превращение, обращение, противопоставление предикату, преобразование по логическому квадрату.
К опосредованным дедуктивным умозаключениям относятся такие умозаключения, как простой категорический силлогизм (вывод в котором получается из двух категорических суждений), а также умозаключения из суждений с отношениями (посылками и заключениями которых являются суждения с отношениями).
К дедуктивным умозаключениям, посылками которых являются сложные суждения, относятся чисто условные дедуктивные умозаключения (посылками которых являются условные суждения), условно-категорические дедуктивные умозаключения (одна из посылок которых является чисто условным суждением, а другая категорическим суждением), разделительно-категорические дедуктивные умозаключения (одна из посылок которых является разделительным суждением, а другая категорическим суждением), а также условно-разделительные дедуктивные умозаключения (одна из посылок которых является условным суждением, а другая разделительным суждением).
Наиболее важными, в силу широкой применимости в СИИ, являются условно-категорические дедуктивные умозаключения, выполняемые по схемам утверждающего (modus ponens) и отрицающего (modus tollens) модусов. Формулы этих модусов имеют следующий вид:
a.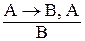 
(modus ponens)
b.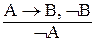 
(modus tollens)
Индуктивными умозаключениями являются умозаключения, в которых совершается переход от знаний об отдельных объектах класса или его частях (подклассах) к знанию обо всем классе в целом. Исходными суждениями здесь, в отличие от дедуктивных умозаключений, являются не общие суждения, а еденичные суждения или частные суждения, а заключениями – общие суждения.
Посылками индуктивных умозаключений выступают суждения, в которых фиксируется полученная опытным путем информация об устойчивой повторяемости некоторого признака (P) у ряда объектов (S1, S2, …, Sn), составляющих некоторый класс объектов (K). Схема умозаключений, в данном случае, имеет вид:
S1 обладает P
S2 обладает P
…
Sn обладает P
Каждый Si Î К обладает Р
С помощью индуктивных умозаключений обобщаются результаты исследований. В зависимости от полноты исследований различают два вида индукции: полную и неполную. Полная индукция предполагает рассмотрение всех объектов класса, неполная – их части.
Традуктивные умозаключения (умозаключения по аналогии) – это такие умозаключения, в которых из сходства объектов по одним признакам делается вывод об их сходстве по другим. По характеру уподобления различают аналогию предметов и аналогию отношений.
Аналогия предметов – это умозаключение, в котором объектом уподобления выступают два единичных предмета , а переносимым признаком свойство, присущее одному из объектов. Схема умозаключений, в данном случае, имеет вид:
А имеет признаки P, Q, S, T,…
В имеет признаки P , Q , S ,…
В, по-видимому, имеет признак T
Аналогия отношений – это умозаключение, в котором объектом уподобления выступают отношения между двумя парами объектов, а переносимым признаком – свойство, присущее одному из этих отношений. Схема умозаключений, в данном случае, имеет вид:
А R1 В, R1 имеет свойства P, Q, S, T,…
С R 2 D , R 2 имеет свойства P , Q , S ,…
R2, по-видимому, имеет свойство T
Действие 1
Результат А Результат В Рис.4.Схема “И”
Действие 2
Результат С Результат D Рис.5. Схема “ИЛИ”
Теоретико-множественные отношения - это отношения между понятиями различной степени общности (надпонятие, подпонятие); отношения между частью и целым; отношения, связывающие множества (классы) с их элементами (экземплярами). Этот класс отношений используется для построения иерархических таксономических (соподчиненных) структур. В таких структурах все свойства надпонятий автоматически присваиваются подпонятиям, (принцип наследования), что позволяет исключать описания повторяющихся сведений. На рис.6 представлены схемы, иллюстрирующие теоретико-множественные отношения.
 |
Рис.6. Схемы, иллюстрирующие теоретико-множественные отношения.
Квантификационные отношения - это отношения, выражающие логические кванторы общности (") и существования ($). Логические кванторы применяются для представления общезначимых утверждений типа "Каждый станок периодически требует профилактического ремонта" и "Существует робот А, который может обслуживать все станки группы В" и т.п. Формальное представление этих отношении опирается на приписывание кванторов высказываниям семантических сетей.
С семантическими сетями связаны такие понятия, как
денотат и концепт. Денотат - это сущность предметной
области, обозначаемая некоторым знаком. Концепт - это
свойство денотата. С понятием знака (выражаемого буквой,
цифрой, словом и т.п.) связаны, в свою очередь, понятие
интенсионала и экстенсионала. Интенсионал знака определяет
содержание связанного с ним понятия. Экстенсионал знака
определяет класс всех его допустимых денотатов.
Например, для понятия "студент" интенсионалом будет
высказывание "Человек, учащийся в институте", а
экстенсионалом - все множество конкретных людей, учащихся
в институтах. В соответствии с вышесказанным различают
интенсиональные и экстенсиональные знания.
Интенсиональные знания - это общие знания о предметной области.
Э кстенсиональные знания - это конкретные знания о предметной области (факты).
В общем случае семантическая сеть, описывающая некоторую предметную область, имеет интенсиональную и экстенсиональную части (подсети).
Интенсиональная подсеть описывает общие знания о моделируемой предметной области. Экстенсиональная подсеть описывает фактические знания о моделируемой предметной области.
Такой подход к представлению знаний с помощью семантических сетей является весьма эффективным, так как позволяет исключить дублирование информации при описании предметных областей.
Лекция №4. Сети фреймов
Время: 2 часа (90 мин.)
Развитием подхода семантических сетей явились так называемые сети фреймов, представляющие собой определенным образом упорядоченные семантические сети.
Для описания событий, объектов и состояний объектов предметных областей здесь используются специальные конструкции, называемые фреймами. В самом простом случае фрейм включает в себя набор характеристик, необходимых для описания той или иной сущности предметной области.
Графически структуры фреймов, используемые для описания событий, объектов и их состояний могут быть представлены следующим образом:
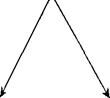
1. Структура фрейма для описания событий.
< Имя события >
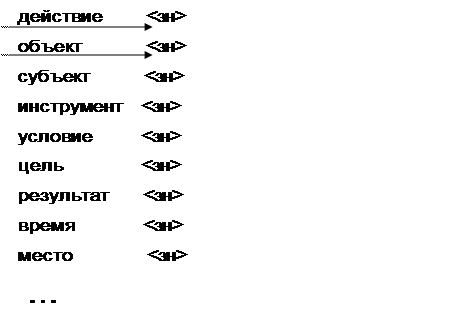
Здесь <зн> – значение той или иной характеристики.
2. Структура фрейма для описания объектов.
<Имя объекта>
 |
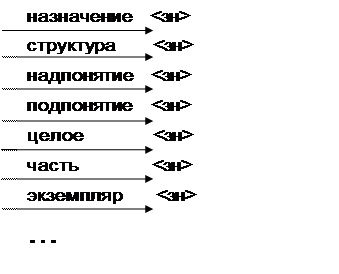3. Структура фрейма для описания состояний объектов.
<Имя состояния объекта>
 |
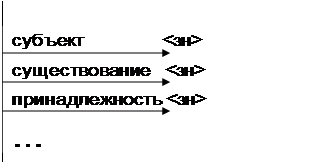Приведенные выше фреймы без указания конкретных имен и значений характеристик представляют собой фреймы-прототипы, используемые для описания конкретных событий и объектов предметных областей. Заполненный фрейм-прототип для конкретного события, объекта или состояния объекта представляет собой уже фрейм-пример или, как еще говорят, фрейм- экземпляр. Характеристики, используемые в структурах фреймов, получили название слотов. Слот, получивший значение, считается
заполненным. В противном случае – пустым. Примерами фреймов-экземпляров могут служить следующие фреймы:
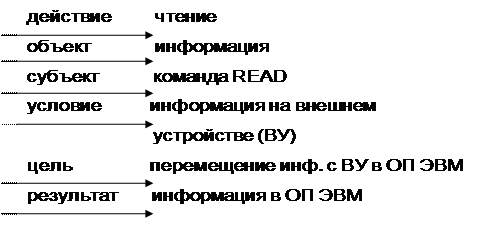
1. Фрейм-пример события «Выполнение команды READ».
Выполнение команды READ
 |
2. Фрейм-пример объекта «Команда READ».
Команда READ
 |
3. Фрейм-пример состояния «Информация на ВУ».
Информация на ВУ
|
4. Фрейм-пример состояния «Информация в ОП ЭВМ».
Информация в ОП ЭВМ
 |
5. Фрейм-пример объекта «Информация».
Информация
*
Здесь звездочкой отмечен самоопределённый объект, т.е. объект, не требующий определения в данном контексте.
Для представления знаний с помощью фреймов используются декларативные языки ролевого типа. Основной конструкцией таких языков является ролевой фрейм, который может быть представлен следующим образом:
<имя фрейма> <R1=V1>, < R2=V2>,…, < Rn=Vn>
Здесь Ri, – имя i-го слота, соответствующего характеристике (роли), используемой для описания некоторой сущности предметной области; Vi, – значение i -го слота.
Используя понятие ролевого фрейма можно определить структуры ролевых фреймов для описания событий, объектов и их состояний следующим образом:
1. Структура ролевого фрейма для описания событий.
Е. <имя события> R.REL E1 = VAL E1,
R.REL E2 = VAL E2,
. . .
R.REL Ek = VAL Ek
где Е – общий идентификатор фреймов событий;
R.REL Ei - i-я характеристика события;
VAL Ei - значение R.REL Ei.
2. Структура ролевого фрейма для описания объектов.
О. <имя объекта> R.REL 01 = VAL 01,
R.REL 02 = VAL 02,
. . .
R.REL 0m = VAL 0m
где О - общий идентификатор фреймов объектов;
R.REL 0i - i-я характеристика объекта;
VAL 0i - значение R.REL 0i.
3. Структура ролевого фрейма для описания состояний объектов.
S. <имя состояния> R.REL S1 = VAL S1,
R.REL S2 = VAL S2,
. . .
R.REL Sn= VAL Sn
где S - общий идентификатор фреймов состояний;
R.REL Si - i-я характеристика состояния объекта;
VAL Si - значение R.REL Si
Используя определенные выше ролевые фреймы-прототипы можно описывать различного рода предметные области в виде наборов фреймов-экземпляров.
Ниже приводятся примеры фреймов-экземпляров, использованных для описания событий, объектов и состояний объектов, соответствующих предыдущим примерам:
1. Описание события «Выполнение команды READ».
Е. READ R.ДЕЙСТВИЕ = 'чтение',
R.ОБЪЕКТ = 'информация',
R.СУБЪЕКТ = 'команда READ',
R.УСЛОВИЕ = 'информация на ВУ',
R.ЦЕЛЬ = 'перемещение информации
с ВУ в ОП ЭВМ',
R.РЕЗУЛЬТ = 'информация в ОП ЭВМ'
2. Описание объекта «Команда READ».
O. READ R.НАЗНАЧ. = 'перемещение информации
с ВУ в ОП ЭВМ',
R.ФОРМАТ = 'формат команды READ'
3. Описание состояния «Информация на ВУ».
S.INF1 R.СУБЪЕКТ = 'информация',
R. ПРИНАДЛ. = 'ВУ'
4. Описание состояния «Информация в ОП ЭВМ».
S.INF2 R.СУБЪЕКТ = 'информация',
R. ПРИНАДЛ. = 'ОП ЭВМ'
5. Описание объекта «Информация».
О.INF *
Здесь символы апострофов заключают в себе значения, являющиеся текстовыми константами. Если же в качестве значений слотов использовать идентификаторы (например, идентификаторы фреймов объекта O.READ и состояний S.INF1 и S.INF2 во фрейме E.READ), то можно устанавливать связи между различными фреймами. Например:
Е. READ R.ДЕЙСТВИЕ = 'чтение',
R.ОБЪЕКТ = 'информация',
R.СУБЪЕКТ = O.READ,
R.УСЛОВИЕ = S.INF1,
R.ЦЕЛЬ = 'перемещение информации
с ВУ в ОП ЭВМ',
R.РЕЗУЛЬТАТ = S.INF2
Таким образом, за счет ссылок фреймы могут связываться друг с другом, образуя весьма сложные структуры, называемые сетями фреймов.
В дополнение к вышеизложенному следует отметить, что со слотами фреймов могут связываться различные процедуры, получившие название присоединенных процедур и используемые для преобразования информации внутри фреймов, а также для вычисления значений слотов с использованием принципа наследования. Они делятся на процедуры-демоны, которые активизируются автоматически и процедуры-слуги, активизируемые по запросам. Однако следует отметить, что процедуры являются лишь возможными, но не обязательными элементами ролевых фреймов.
Текст лекции
Вопросы логического вывода знаний на сетях фреймов удобнее всего рассмотреть с точки зрения их использования в системах искусственного интеллекта. С этих позиций следует отметить, что сети фреймов были с успехом использованы в вопросно-ответных системах (ВОС), обеспечивающих автоматическое формирование ответов на вопросы пользователей.
Механизм выводов в ВОС представляет собой совокупность специализированных процедур обработки знаний, обеспечивающих формирование ответов на те или иные вопросы пользователей о сущностях предметных областей.
Архитектура системы, базирующейся на сети фреймов,
приведена на рис.8. Она включает в себя следующие компоненты: программу управления диалогом, анализирующую тип входных предложений-вопросов и осуществляющую вызов соответствующих процедур выводов; процедуры выводов, формирующие ответы на вопросы с использованием сети; сеть, содержащую знания о предметной области.
 | |||||||||
| | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 |  | | |||||
 | |||||||
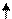Рис.8. Архитектура системы, базирующейся на сети фреймов.
Анализ спектра вопросов к ВОС позволяет выделить два их основных вида, а именно:
(1) – вопросы, ответы на которые формируются путем спецификации характеристик сущностей предметных областей;
(2) – вопросы, ответы на которые формируются в результате
вычисления отношений между сущностями предметных областей.
К первому виду вопросов относятся вопросы о значениях различных характеристик объектов и событий предметных областей. Информация о значениях этих характеристик имеется во фреймах-экземплярах, описывающих данные сущности. Их нахождение путем поиска, по существу, равнозначно ответу на вопросы. Вопросы данного вида могут быть представлены следующим образом:
1. Вопросы о значениях характеристик объектов.
R.АВС (О.СВА)=?
Например, «Каково назначение команды READ ?»: R.НАЗНАЧЕНИЕ (О.READ)=?
2. Вопросы о значениях характеристик событий.
R.АВС (Е.СВА)=?
Например, «Каков результат выполнения команды READ ?»: R.РЕЗУЛЬТАТ (Е.READ)=?
Формирование ответов на такие вопросы осуществляется путем поиска значений искомых характеристик в соответствующих слотах фреймов-экземпляров базы знаний, описывающих тот или иной объект или событие.
Технологически это выглядит следующим образом. Сначала в базе знаний, физически реализующей сеть фреймов, ищется соответствующий фрейм-экземпляр объекта или события, а затем искомая характеристика (слот) в системе слотов найденного фрейма-экземпляра. Значение этого слота выделяется и выводится в качестве ответа на вопрос.
Если это значение является текстовой константой, то оно не подвергается никакой предварительной обработке. В противном случае (т.е. когда выводимое значение представляет собой ссылку на другой фрейм базы знаний) необходимо предварительно преобразовать выводимый ответ в форму, понятную пользователю, т.е. осуществить его интерпретацию.
Ко второму виду вопросов относятся вопросы о наличии связей между событиями, о сходстве и различии событий, о причинах и следствиях реализации того или иного события и т.п. Вопросы данного вида могут быть представлены следующим образом:
1. Вопросы о связях между событиями.
СВЯЗЬ (Е.АВС, Е.СВА)=?
Например: «Какова связь между выполнением команд ОРЕN и READ?»:
СВЯЗЬ (Е.ОРЕN, Е.READ)=?
2. Вопросы о сравнении событий.
СРАВНЕНИЕ (Е.АВС, Е.СВА)=?
Например: «В чем сходство / различие в выполнении команд READ и WRITE? »:
СРАВНЕНИЕ (Е.READ, Е.WRITE)=?
3. Вопросы об анализе того или иного события.
АНАЛИЗ (Е.АВС)=?
Например: «Каковы причины / следствия выполнения команды READ?»:
АНАЛИЗ (Е.READ)=?
Формирование ответов на такого рода вопросы осуществляется путем выполнения умозаключений по следующим правилам:
а. Правила для выявления связей между событиями:
1. (R.РЕЗУЛЬТАТ (Е.АВС) = R.УСЛОВИЕ (Е.СВА)) =>
=> R.РАНЬШЕ (Е.АВС, Е.СВА)
2. (R.УСЛОВИЕ (Е.АВС) = R.РЕЗУЛЬТАТ (Е.СВА)) =>
=> R.ПОЗЖЕ (Е.АВС, Е.СВА)
Интерпретация правил следующая: «Если результат события Е.АВС является условием события Е.СВА, то событие Е.АВС реализуется перед событием Е.СВА» и «Если условие события Е.АВС является результатом события Е.СВА, то событие Е.АВС реализуется после события Е.СВА».
б. Правила для сопоставления событий:
1. (R.РЕЗУЛЬТАТ (Е.АВС) = R. РЕЗУЛЬТАТ (Е.СВА)) =>
=> R.ЭКВИВАЛЕНТНО (E.АВС, Е.СВА)
2. (R. РЕЗУЛЬТАТ (Е.АВС) : R. РЕЗУЛЬТАТ (Е.СВА)) =>
=> R. ПРОТИВОПОЛОЖНО (E.АВС, Е.СВА)
Здесь символ «:» определяет противоположность результатов двух событий, характеризуя их таким образом.
в. Правила для анализа события:
1. (R.УСЛОВИЕ (Е.АВС) = R.РЕЗУЛЬТАТ (Е.СВА)) =>
=> R.ПРИЧИНА (Е.СВА , E.АВС)
2. (R.РЕЗУЛЬТАТ (Е.АВС) = R.УСЛОВИЕ (Е.СВА)) =>
=> R.СЛЕДСТВИЕ (Е.СВА , E.АВС)
Понятно, что приведенный выше перечень вопросов и правил не является исчерпывающим и может быть расширен и дополнен. Сам спектр входных вопросов, в конечном счете, может служить критерием мощности той или иной ВОС, а «надежность» правил вывода – критерием их качества.
Следует отметить также, что наиболее простым способом вывода на сетях фреймов и семантических сетях является использование принципа наследования, когда новое свойство сущности выводится через его наличие у соответствующего надпонятия.
Текст лекции
Для понимания существа нестрогого вывода удобнее всего рассмотреть способ организации базы правил и принципы функционирования механизма выводов на конкретном примере некоторой ЭС.
В этих целях рассмотрим экспертную систему МYСIN, которая предназначена для решения задач медицинской диагностики инфекционных заболеваний.
Все множество продукций МYСIN можно представить в виде совокупности И/ИЛИ графов, в самых нижних узлах которых располагаются основные системные данные (исходные факты Фi), а в самых верхних – заключения (Сj), выводимые системой.
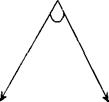
Каждое правило МYСIN может включать одно или несколько условий, соединенных связкой "И". Графически такое правило можно представить в виде дерева, приведенного на рис.10.
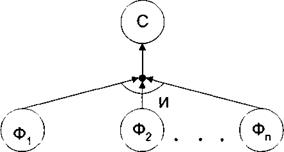
Рис.10. Графическое представление правила
В случае, когда имеется несколько правил, из которых выводится одно и то же заключение, используется связка "ИЛИ" (см. рис.11.).
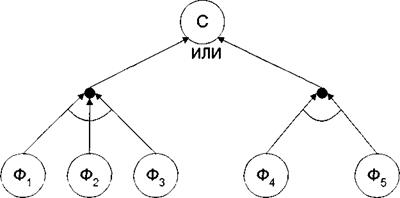
Рис.11. Графическое представление двух правил, из которых выводится одно заключение
Следует заметить, что в системе МYСIN все вершины ИЛИ являются бинарными, что достигается за счет искусственного сведения такого рода вершин произвольной арности к совокупности бинарных.
Система МYСIN функционирует в такой области, где решения редко принимаются наверняка. Поэтому разработчики этой системы объединили со стандартным механизмом выводов некоторую простую теорию правдоподобного рассуждения, позволяющую устанавливать для каждого заключения в И/ИЛИ дереве так называемый фактор уверенности (ФУ), варьируемый от 0 до 1. Согласно этой теории каждый факт, поставляемый пользователем системе, снабжается фактором достоверности (ФД), а каждое правило имеет свой фактор ослабления (ФО), вносимый в вывод и указывающий на "надежность", присущую той или иной продукции. Факторы достоверности и ослабления также принимают значения в диапазоне от 0 до 1.
На основе такого рода данных вычисляются факторы уверенности для каждого сделанного системой заключения. Осуществляется это с помощью двух следующих правил:
(1) – в вершинах типа "И" наименьший фактор
достоверности исходных данных умножается на фактор
ослабления, вносимый продукцией, и полученное значение
приписывается заключению в качестве его фактора
уверенности (благодаря этому заключение никогда не будет
иметь большую "силу", чем самое "слабое" из
поддерживающих его свидетельств-фактов). Формально это
выглядит следующим образом:
<ФУ заключения> = <min ФД исход. факта> х <ФО, вносимый правилом >;
(2) – в вершинах типа "ИЛИ" факторы уверенности,
вносимые правилами, подкрепляют друг друга и могут
обеспечивать большую "силу" заключению, чем каждое из
правил в отдельности. Вычисления осуществляются по
следующей формуле:
<Ф.У. заключения> = <Ф.У. заключения 1-го правила> + <Ф.У. заключения 2-го правила> - <Ф.У. заключения 1-го правила> х <Ф.У. заключения 2-го правила>.
Следует заметить, что если правдоподобность некоторого заключения, определяемая его фактором уверенности, падает ниже некоторого значения (в МYСIN оно равно 0,2), то оно отвергается и в процессе дальнейшего вывода не участвует. На рис.12. приводится пример И/ИЛИ дерева для вычисления фактора уверенности одного финального заключения-гипотезы.
| А=0,8
|
0=0,75+0,65-0,49=0,91 А=1| А=0,9 I А=0,8 А=0 |
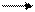
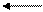
Е=0,8 Е=0,2 Е=0,9 Е=0,7
Е – факторы достоверности исходных фактов
А – факторы ослаблений, вносимые продукциями
С – вычисляемые факторы уверенности.
Рис.12. И/ИЛИ дерево для вычисления фактора уверенности заключения-гипотезы
На приведенном примере хорошо видна направленность вывода (снизу-вверх), соответствующая восходящему выводу.
Текст лекции
Экспертная система представляет собой программный комплекс, содержащий знания специалистов из определенной предметной области, обеспечивающий консультациями менее квалифицированных пользователей для принятия экспертных решений. Схема экспертной системы приведена на рис.13.
В состав современных экспертных систем входят следующие основные компоненты: база знаний, механизм выводов, подсистема объяснений, редактор базы знаний и интерфейс пользователя.
База знаний представляет собой совокупность знаний о предметной области, организованных в соответствии с принятой моделью представления знаний.
Механизм выводов (МВ), представляет собой программу, обеспечивающую вывод решений формулируемых пользователем задач на основе знаний, хранящихся в базе знаний.
Подсистема объяснений представляет собой программу, которая позволяет пользователю выполнить трассировку цепочки логического вывода и получить мотивировку умозаключений на каждом этапе этой цепочки.
Редактор базы знаний – это программа, предназначенная для ввода в базу знаний определенных знаний о предметной области, необходимых для выполнения выводов.
Интерфейс пользователя – это программа, обеспечивающая диалог пользователя с ЭС при вводе запросов на решение экспертных задач, получении результатов и объяснений.
Рис.13 Структурная схема экспертной системы.
Инженер по знаниям – специалист по системам искусственного интеллекта, помогающий эксперту вводить знания в базу знаний ЭС.
Эксперт – специалист в предметной области, способный принимать экспертные решения.
Пользователь ЭС является специалистом в данной предметной области, квалификация которого уступает квалификации эксперта.
Экспертная система функционирует в двух режимах: режиме приобретения знаний и в режиме консультации.
В режиме приобретения знаний база знаний ЭС загружается необходимой информацией (знаниями), которая позволяет в режиме консультации решать задачи экспертизы.
В режиме консультации пользователь обращается к ЭС за получением той или иной консультации относительно интересующей его проблемы. При этом, если его интересует объяснение того, как был получен результат, то он может получить трассировку вывода.
ЭС можно классифицировать по различным признакам. По типу предметных областей различают статические и динамические экспертные системы. Статические ЭС – работают с предметными областями (данными), которые не меняются во времени. Динамические ЭС – сопряжены с датчиками объектов и работают в режиме реального времени с непрерывно меняющимися и поступающими в систему данными.
По степени интеграции с другими программами различают автономные и гибридные ЭС.
Автономные ЭС – это такие системы, которые работают в режиме консультации для решения таких экспертных задач, когда не требуется привлечение традиционных методов обработки данных (расчетов, моделирования и т. п.)
Гибридные ЭС – это программные комплексы, агрегирующие стандартные пакеты прикладных программ для решения сложных задач с привлечением экспертных знаний.
По степени сложности ЭС можно разделить на простые ЭС (до 500 правил в базе знаний), ЭС средней сложности (от 500 до 1500 правил) и сложные ЭС (свыше 1500 правил).
Класс решаемых задач характеризует экспертные системы как системы решающие задачи диагностики, прогнозирования и д.р.
В ходе работ по созданию ЭС сложилась определенная технология их разработки, включающая следующие этапы:
(1) – этап идентификации;
(2) – этап концептуализации;
(3) – этап формализации;
(4) – этап реализации;
(5) – этап тестирования;
(6) – этап опытной эксплуатации
На этапе идентификации выявляются цели и общая концепция разработки, определяются задачи, подлежащие решению, выявляются требования будущих пользователей.
На этапе концептуализации проводится содержательный анализ класса предметных областей, на которые ориентирована разработка, выделяются используемые в предметных областях сущности и взаимосвязи между ними, определяются типы и методы решения задач, реализуемые разрабатываемой системой.
На этапе формализации определяются способы представления всех типов знаний, используемых в разработке, фиксируются способы интерпретации знаний, моделируется работа системы "на бумаге".
На этапе реализации осуществляется создание программного и информационного обеспечения разрабатываемой системы.
На этапе тестирования проверяется компетентность разрабатываемой системы.
На этапе опытной эксплуатации проверяется пригодность разрабатываемой системы для конечных пользователей.
По результатам двух последних этапов возможна коррекция и модификация разрабатываемой системы.
При разработке ЭС используется концепция "прототипа", суть которой состоит в том, что разработчики не пытаются сразу создать конечный продукт. На начальном этапе разработки ЭС создается ее прототип, который должен удовлетворять следующим требованиям:
(1) – решать типовые задачи конкретного приложения;
(2) – время и трудоемкость его разработки должны быть весьма небольшими.
Для решения такой задачи обычно используют инструментальные среды, позволяющие быстро создавать и отлаживать экспериментальную ЭС, а затем ее уже переписывают с использованием того или иного универсального языка программирования, что обеспечивает окончательному варианту системы минимальный объем памяти и высокое быстродействие.
Инструментальные средства, используемые для создания прикладных ЭС, можно разделить на четыре основные группы:
(1) – универсальные и функциональные языки программирования (БЕЙСИК, ПАСКАЛЬ, СИ, ЛИСП и др.);
(2) – языки инженерии знаний (ПРОЛОГ, KRL, FRL и др.);
(3) – инструментальные среды (GURU, CLIPS, G2 и др.);
(4) – оболочки (EMYCIN, ЭКО, ЭКСПЕРТ и др.).
В приведенной классификации инструментальные средства перечислены в порядке убывания трудозатрат, которые необходимы для создания ЭС.
Автор
к.т.н., проф.
Миронов А.С. / Миронов А.С. /
ЛЕКЦИИ
по дисциплине 1423 Системы искусственного интеллекта
для студентов 5 курса факультета ИТ
специальности 230101
«Вычислительные машины, комплексы, системы и сети»
Обсуждены на заседании кафедры
«___» _______________ 2007 г.
Протокол № _____
Москва, 2007
Общие положения
1.1 Цели дисциплины
Целью дисциплины является изложение основ теории систем искусственного интеллекта
1.2 Рекомендуемая литература
1.2.1 Основная:
1) Миронов А.С. Системы искусственного интеллекта: Учебное пособие. – М.: МГУПИ, 2007. – 48с.
2) Костров Б.В. и др. Основы искусственного интеллекта. – М: «ДЕСС», «ТехБух», 2007. – 192с.
1.2.2 Дополнительная литература:
1) Башмаков А.И., Башмаков И.А. Интеллектуальные информационные технологии. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 304с.
2) Рассел С., Норвиг П. Искусственный интеллект: современный подход. – М.: «Вильямс», 2006. – 1408с.
3) Джарратано Д., Райли Г. Экспертные системы: принципы разработки и программирование. – М.: «Вильямс», 2007. – 1152с.
2 Л екция №1. Основные понятия и определения.
Время: 2 часа (90 мин.)
2.1 Основные вопросы
- основные понятия СИИ.
Текст лекции
Системы искусственного интеллекта (СИИ) могут быть определены как интеллектуальные компьютерные программы, использующие знания и процедуры логических выводов для решения задач. Основными видами СИИ являются вопросно-ответные и экспертные системы. Архитектура СИИ представлена на рис.1.
СИИ
База знаний
Входная информация
Механизм обраб. знаний
Выходная информация
Рис.1. Архитектура СИИ.
Входной информацией для СИИ являются различные вопросы или факты, вводимые пользователем. Механизм обработки знаний связывает входную информацию с информацией, хранящейся в базе знаний, и на этой основе осуществляет логический вывод целевых заключений, выдаваемых пользователю в качестве результатов работы системы.
Знаниями принято называть формализованную в соответствии с определенными структурными правилами информацию, которую СИИ могут использовать при выполнении логических выводов. Иными словами, обработка знаний на ЭВМ представляет собой обработку их содержимого с помощью правил преобразования, адекватных тому или иному классу предметных областей.
При создании СИИ наиболее важной и сложной проблемой является проблема формализации знаний о предметных областях. Эта проблема получила название проблемы представления и обработки знаний. Решение данной проблемы заключается в разработке систем представления знаний (СПЗ).
Под СПЗ понимаются средства, позволяющие описывать знания о тех или иных предметных областях, а также выводить новые знания на основе уже имеющихся. Основу СПЗ составляет модель представления знаний (МПЗ) и соответствующая ей модель вывода знаний (МВЗ). Важное место в СПЗ занимает язык представления знаний (ЯПЗ), выразительные возможности которого определяются лежащей в его основе МПЗ.
Различают логические и эвристические МПЗ. Логические МПЗ базируются на использовании исчисления предикатов. Знания здесь выражаются с помощью средств формальной системы. В отличие от логических эвристические МПЗ (семантические сети, сети фреймов, продукционные правила) имеют для этого разнообразный набор средств. В основе методологии формализации знаний лежит такая дисциплина, как формальная логика.
В основе логических моделей представления знаний лежит понятие формальной логической системы (теории). Для описания теории вводится множество её базовых элементов, называемых алфавитом теории. Определяются правила построения правильных предложений (формул) теории из базовых элементов. Часть правильно построенных формул объявляются аксиомами (априори истинными формулами). Задаются, также, правила вывода новых формул из других правильно построенных формул.
Данный подход лежит в основе организации многих дедуктивных СИИ. В соответствии с ним база знаний описывается в виде предложений и аксиом теории, а механизм выводов реализует построение новых предложений из имеющихся в базе знаний. На вход СИИ поступает описание задачи в виде предложения (теоремы), которое явно не представлено в базе знаний. Но если оно верно с позиций имеющихся знаний, то может быть выведено из содержимого базы знаний путем выполнения механизмом выводов правил вывода. Процесс работы механизма выводов называют доказательством теорем.
С практической и теоретической точек зрения наиболее важной формальной теорией является исчисление предикатов. В нем предложения расчленяются на субъекты и предикаты. Расчленение предложения на субъект и предикат реализуется путем его соотнесения с логической функцией одной переменной P(X), выражающей свойство субъекта и называемой одноместным (унарным) предикатом. Если же предложение выражает отношение между несколькими субъектами, то с ними связывают n-местную логическую функцию P(X1, X2,…,Xn), называемую n -местным ( n -арным) предикатом.
В исчислении предикатов используются различные правила вывода, основными из которых являются правило подстановки и правило отделения.
В соответствии с правилом подстановки в формулу, которая уже выведена, можно вместо некоторого высказывания подставить любое другое во все места вхождения заменяемого высказывания.
В соответствии с правилом отделения из истинности высказываний a и a®b выводится истинность высказывания b (правило modus ponens).
Модифицированное исчисление предикатов лежит, также, в основе систем логического программирования. Здесь используются специальные классы логических формул, называемые хорновскими дизьюнктами. В качестве метода логического вывода (доказательства) используется метод резолюций.
Наиболее известной реализацией, среди таких систем, является система программирования Турбо-Пролог. В логической программе, в общем случае, описываются множество объектов, их свойств и отношений между объектами, а также правила вычисления ответов на возможные запросы пользователей.
Лекция №2.Логические основы СИИ
Время: 2 часа (90 мин.)
Текст лекции
Формальная логика занимается изучением форм и законов мышления. Одной из главных ее задач является описание правильных человеческих рассуждений. Особый интерес к логике возник с появлением ЭВМ, когда была поставлена задача, научить машину «рассуждать».
Основными формами мышления, изучаемыми в логике, являются: понятие, суждение и рассуждение.
Первая форма мышления – понятие. Понятие о предмете составляет совокупность признаков предмета. Всякое понятие обладает содержанием – совокупностью признаков, определяющих данное понятие и объемом – совокупностью объектов, входящих в данное понятие.
В соответствии с этим определяют интенсионал и экстенсионал понятия. Интенсионал – это совокупность признаков понятия, а экстенсионал – перечисление конкретных его представителей.
При определении понятий различают реальное и номинальное определения. Типичным способом реальных определений понятий является определение через ближайшее родовое (более общее) понятие и указание видового отличия.
При номинальном определении понятий речь идет о выборе имени для понятия, определяемого через перечисление видовых.
Связь между объемом и содержанием понятий выражается в законе обратного отношения: если два понятия сравнимы и содержание первого из них больше, чем содержание второго, то объем второго понятия больше объема первого понятия.
С этим законом связаны способы обобщения (т.е. перехода от понятий с меньшим объемом и большим содержанием к понятиям с большим объемом и меньшим содержанием) и ограничения (т.е. перехода от понятий с большим объемом и меньшим содержанием к понятиям с меньшим объемом и большим содержанием).
По объему понятия делятся на пустые (реально не существующие), еденичные и общие. По содержанию понятия делятся на положительные и отрицательные (присутствуют или нет определенные признаки в понятии), безотносительные и относительные, сравнимые и несравнимые.
Сравнимые понятия (т.е. имеющие общие признаки в содержании) бывают совместимыми, (объемы понятий имеют совпадающую часть) и несовместимыми. Выделяют три вида отношений совместимости: равнозначность, пересечение и подчинение объемов. Существуют и три вида отношений несовместимости: соподчинение, противоположность, противоречие.
Одной из основных операций над объемом и содержанием понятий является деление понятия (т.е. деление родового понятия на множество видовых понятий). При её выполнении различают делимое понятие, основание деления (признаки) и члены деления (множество понятий, видовых по отношению к исходному). Частным случаем деления является дихотомическое деление (т.е. деление на два класса с противоречивыми признаками). Практическое применение операции деления понятий связано с классификацией, целью которой является приведении знаний о предметной области в систему.
Вторая форма мышления – суждение. В суждениях содержится информация о предметах и отношениях между ними. Соответствие или не соответствие суждения реальности определяет его истинность или ложность. С грамматической точки зрения, суждение – это повествовательное предложение естественного языка (ЕЯ).
Суждение может содержать логический квантор, выражаемый в ЕЯ словами «все», «некоторые» и т.п.
По структуре суждения делятся на простые, выражаемые простыми предложениями ЕЯ и сложные, выражаемые сложными предложениями ЕЯ. Простое суждение состоит из субъекта S (логическое подлежащее, определяющее то, о чем идет речь), предиката P (логическое сказуемое, определяющее то, что утверждается или отрицается о субъекте), логической связки «есть» или «не есть», выражающей связь между субъектом и предикатом (в ЕЯ она может лишь подразумеваться) и, возможно, логического квантора.
Простые суждения делятся на атрибутивные, выражающие принадлежность или не принадлежность свойств объекту или классу объектов, суждения об отношениях, выражающие наличие или отсутствие отношений между объектами или классами объектов и суждения о существовании (экзистенциональные суждения), говорящие о существовании или не существовании объектов или классов объектов.
По качеству простые суждения делятся на утвердительные и отрицательные. С количественной стороны простые суждения делятся на еденичные (в них что-либо утверждается или отрицается об одном объекте), частные (в них что-либо утверждается или отрицается о части объектов некоторого класса), и общие (в них что-либо утверждается или отрицается обо всех объектах некоторого класса).
Еденичные утвердительные и отрицательные суждения имеют логические формы “S есть P” и “ S не есть P ”.
Частноутвердительные и частноотрицательные суждения имеют логические формы “Некоторый S есть P” и “Некоторый S не есть P”.
Общеутвердительные и общеотрицательные суждения имеют логические формы “Всякий S есть P” и “Всякий S не есть P”.
Различают сравнимые и несравнимые суждения. Сравнимые суждения имеют одни те же субъекты и предикаты, но различаются связкой или квантором. Несравнимые суждения имеют различные субъекты и предикаты.
Сложные суждения – это суждения, состоящие из нескольких простых суждений, связанных между собой различными логическими связками. Связки выступают важнейшими элементами сложных суждений, т.к. определяют их структуру. Основными видами сложных суждений являются соединительные, разделительные, условные суждения и суждения эквивалентности.
Соединительные суждения представляют собой связь двух и более простых суждений с помощью логической связки “И” и имеют логическую форму pÙqÙ…Ùr.
Разделительные суждения представляют собой связь двух и более простых суждений с помощью логической связки “ИЛИ” и имеют логическую форму pÚqÚ…Úr.
Условные суждения состоят из двух простых суждений, связанных связкой “ЕСЛИ, ТО” и имеют логическую форму p®q.
Суждения эквивалентности состоят из двух простых суждений, связанных связкой “ЕСЛИ И ТОЛЬКО ЕСЛИ, ТО” и имеют логическую форму p~q.
Третья форма мышления – рассуждение. Простейшей формой рассуждений являются умозаключения. Посредством умозаключений из одного или нескольких суждений (посылок) получают новое суждение (заключение). Переход от посылок к заключению называется логическим выводом. Возможность вывода заключения из посылок обеспечивается наличием логической связи между ними. Истинные с точки зрения логики выводы формируются путем применения корректных правил вывода.
Умозаключения обычно записываются в следующем виде (форме):
А1, А2, …,Аn ├ B,
где А1, А2, …,Аn – посылки; B – заключение; “├”– знак логического вывода. Допустима еще одна форма записи умозаключений в виде дроби:
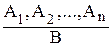
Логический вывод – это, в общем случае, многоэтапный процесс перехода от посылок к заключениям и далее от полученных заключений (как новых посылок) и исходных посылок к новым заключениям. Выполняется этот процесс в виде элементарных актов, каждый из которых есть шаг вывода, на котором применяется соответствующее правило вывода. Вывод за один шаг называется непосредственным выводом.
По характеру связи между знаниями, выраженными в посылках и заключениях, умозаключения классифицируются как:
– дедуктивные (от общего знания к частному знанию);
– индуктивные (от частного знания к общему знанию);
– традуктивные (от частного знания к частному знанию).
При выполнении дедуктивных умозаключений считается, что истинные посылки порождают только истинные заключения. В соответствии с характером посылок, которые могут быть простыми (простыми атрибутивными суждениями, называемыми также категорическими) или сложными суждениями различают простые и сложные дедуктивные умозаключения.
В зависимости от количества посылок дедуктивные умозаключения делятся на непосредственные, в которых заключение выводится из одной посылки, и опосредованные, в которых заключение выводится из двух посылок.
К непосредственным дедуктивным умозаключениям относятся такие умозаключения, как превращение, обращение, противопоставление предикату, преобразование по логическому квадрату.
К опосредованным дедуктивным умозаключениям относятся такие умозаключения, как простой категорический силлогизм (вывод в котором получается из двух категорических суждений), а также умозаключения из суждений с отношениями (посылками и заключениями которых являются суждения с отношениями).
К дедуктивным умозаключениям, посылками которых являются сложные суждения, относятся чисто условные дедуктивные умозаключения (посылками которых являются условные суждения), условно-категорические дедуктивные умозаключения (одна из посылок которых является чисто условным суждением, а другая категорическим суждением), разделительно-категорические дедуктивные умозаключения (одна из посылок которых является разделительным суждением, а другая категорическим суждением), а также условно-разделительные дедуктивные умозаключения (одна из посылок которых является условным суждением, а другая разделительным суждением).
Наиболее важными, в силу широкой применимости в СИИ, являются условно-категорические дедуктивные умозаключения, выполняемые по схемам утверждающего (modus ponens) и отрицающего (modus tollens) модусов. Формулы этих модусов имеют следующий вид:
a. 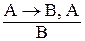(modus ponens)
b. 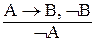(modus tollens)
Индуктивными умозаключениями являются умозаключения, в которых совершается переход от знаний об отдельных объектах класса или его частях (подклассах) к знанию обо всем классе в целом. Исходными суждениями здесь, в отличие от дедуктивных умозаключений, являются не общие суждения, а еденичные суждения или частные суждения, а заключениями – общие суждения.
Посылками индуктивных умозаключений выступают суждения, в которых фиксируется полученная опытным путем информация об устойчивой повторяемости некоторого признака (P) у ряда объектов (S1, S2, …, Sn), составляющих некоторый класс объектов (K). Схема умозаключений, в данном случае, имеет вид:
S1 обладает P
S2 обладает P
…
Sn обладает P
Каждый Si Î К обладает Р
С помощью индуктивных умозаключений обобщаются результаты исследований. В зависимости от полноты исследований различают два вида индукции: полную и неполную. Полная индукция предполагает рассмотрение всех объектов класса, неполная – их части.
Традуктивные умозаключения (умозаключения по аналогии) – это такие умозаключения, в которых из сходства объектов по одним признакам делается вывод об их сходстве по другим. По характеру уподобления различают аналогию предметов и аналогию отношений.
Аналогия предметов – это умозаключение, в котором объектом уподобления выступают два единичных предмета , а переносимым признаком свойство, присущее одному из объектов. Схема умозаключений, в данном случае, имеет вид:
А имеет признаки P, Q, S, T,…
В имеет признаки P , Q , S ,…
В, по-видимому, имеет признак T
Аналогия отношений – это умозаключение, в котором объектом уподобления выступают отношения между двумя парами объектов, а переносимым признаком – свойство, присущее одному из этих отношений. Схема умозаключений, в данном случае, имеет вид:
А R1 В, R1 имеет свойства P, Q, S, T,…
С R 2 D , R 2 имеет свойства P , Q , S ,…
R2, по-видимому, имеет свойство T
Дата: 2018-11-18, просмотров: 638.
