Задача 20
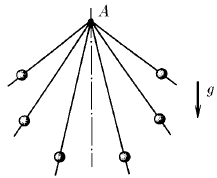
Из точки А по спицам с разным наклоном одновременно начинают скользить без трения маленькие бусинки. На какой кривой будут находиться бусинки в момент времени t?
Ответ: хочу услышать от вас, даю на выбор: 1) ромб, 2) парабола, 3) окружность, 4) гипербола характерный размер фигуры, которую вы считаете правильной, найдите сами.
Задача 21
Свободно падающее тело пролетело мимо точки А со скоростью v А. С какой скоростью оно пролетит мимо точки В, находящейся на h ниже точки А?
Ответ: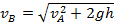 
Задача 22
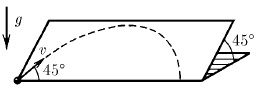По гладкой наклонной плоскости со скоростью v пускают шарик. Какое расстояние по горизонтали он пройдет, прежде чем скатится с плоскости? Плоскость наклонена к горизонту под углом 45°. Начальная скорость шарика образует угол 45° с горизонтальным краем плоскости.
Ответ: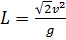 
Задача 23
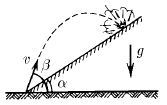Из подствольного гранатомета ведут стрельбу по укрытиям расположенным на склоне горы. На каком расстоянии от стрелка будут падать гранаты, если их начальная скорость v, угол наклона горы α и угол стрельбы по отношению к горизонту β?
Ответ: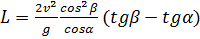 
Задача 24
Утка летела по горизонтальной прямой с постоянной скоростью u. Неопытный охотник бросил в нее камень, причем бросок был сделан без упреждения, то есть в момент броска скорость камня v была направлена на утку под углом α к горизонту. На какой высоте летела утка, если камень все-таки попал в нее?
Ответ: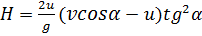 
Задача 25
В трубу длины L, наклоненную под углом α к горизонту, влетает шарик с горизонтальной скоростью v. Определите время пребывания шарика в трубе, если удары шарика о ее стенки упругие.
Ответ: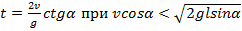 
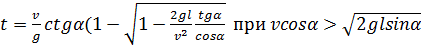
Задача 26
Какую минимальную скорость должен иметь камень, брошенный человеком, чтобы он перелетел дом высоты H и длины L, если бросок совершается с высоты h и для броска человек может выбрать любое место?
Ответ: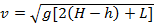 
Задача 27
С какой скоростью должен лететь спутник вокруг Земли, чтобы, все время «падая» с ускорением g, двигаться по круговой орбите? Высота полета спутника 600 км над уровнем моря, радиус Земли 6400 км, а ускорение свободного падения на высоте 600 км равно 8,2 м/с2.
Ответ: 7.58 км/с
Задача 28
Самолеты летят по одной прямой навстречу друг другу с одинаковой скоростью v. Предельная дальность обнаружения ими друг друга l. Один самолет после обнаружения другого совершает разворот, не меняя модуля скорости, и летит параллельно второму самолету. При каком постоянном ускорении разворачивающегося самолета самолеты потеряют друг друга из вида в конце разворота?
Ответ: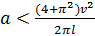 
Задача 29
Сферический резервуар, стоящий на земле, имеет радиус R. При какой наименьшей скорости брошенный с земли камень может перелететь через резервуар, лишь коснувшись его вершины?
Ответ: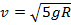 
Задача 30
Снаряд вылетает из пушки со скоростью v под углом α к горизонту. Какое время снаряд приближается к пушке?
Ответ: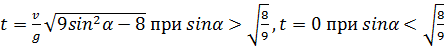 
1.4. Преобразование Галилея. (Одно занятие)
Задача 31
Одна из звезд нашей вселенной покоится, а все остальные звезды разлетаются от нее в разные стороны со скоростями, пропорциональными расстояниям от них до покоящейся звезды. Какую картину движения обнаружит наблюдатель, движущийся вместе с другой звездой нашей вселенной?
Ответ: не скажу
Задача 32
Какой будет продолжительность полета из Новосибирска в Москву и обратно, если полет проходит по прямой, а в течение всего времени полета дует ветер со скоростью u под углом α к трассе? Скорость самолета относительно воздуха v, длина трассы L. При каком направлении ветра продолжительность полета максимальна?
Ответ: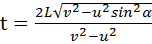 
, когда ветер дует вдоль трассы
Задача 33
Тело налетает на стенку со скоростью v под углом α к линии, перпендикулярной стенке. Определите скорость тела после упругого удара, если стенка: а) неподвижна; б) движется перпендикулярно самой себе со скоростью w навстречу телу; в) движется под углом β к линии, перпендикулярной ей самой, со скоростью w навстречу телу.
Ответ: а)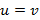 
; б) 
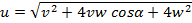; в)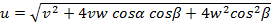 
Задача 34
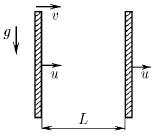
Тело влетает горизонтально со скоростью v в пространство между двумя вертикальными стенками, которые перемещаются со скоростью u. Определите скорость тела после n-го удара о переднюю стенку. Расстояние между стенками L. Удары абсолютно упругие. Ускорение свободного падения g.
Ответ: проекции скорости будут равны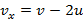 
; 
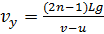
Задача 35
Между двумя стенками со скоростью v летает шарик. Одна из стенок начинает с бесконечно-малой скоростью приближаться к другой. Начальное расстояние между стенками L. Какой будет скорость шарика, когда расстояние между стенками будет L /2? Столкновения шарика со стенками упругие.
Ответ: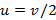 
Задача 36
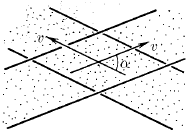Два пучка частиц, движущихся с одинаковой по модулю скоростью v, пересекаются под углом α. Соударения частиц происходят в ограниченной области. Перейдем к системе отсчета, в которой скорости частиц равны по модулю и противоположны по направлению. Казалось бы, теперь область пересечения – весь объем пучков, и поэтому число соударений в единицу времени должно быть больше. Объясните получившееся противоречие.
Ответ: кто списал тот молодец, посмотрим, кто сможет объяснить.
Задача 37
Идет отвесный дождь. Скорость капель u. По асфальту со скоростью v скользит мяч. Найдите соотношение количества воды, попавшей на мяч, со случаем, когда мяч остается неподвижным. Изменится ли ответ, если мяч не круглый?
Ответ: Задачу только придумал и пока не решал.
Движение со связями.
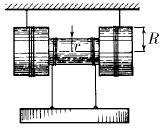Задача 38
Угловая скорость катушки равна ω, радиус внутреннего цилиндра r, а радиус внешних цилиндров R. Каковы скорости оси катушки и груза относительно земли?
Ответ: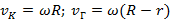 
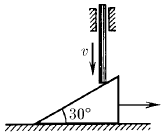
Задача 39
На клине с углом α лежит монета. С каким наименьшим ускорением должен двигаться клин по горизонтальной плоскости, чтобы монета свободно падала вниз?
Ответ: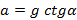 
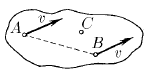
Задача 40
Скорости точек A и B твердого тела равны v. Скорость точки С, находящейся в плоскости прямой AB и вектора v, равна u > v. Найдите проекцию скорости точки С на ось, перпендикулярную указанной плоскости.
Ответ: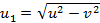 
Задача 41
Постройте траектории точек колеса, катящегося без проскальзывания по рельсу. Рассмотрите случаи когда точки находятся от оси колеса на расстоянии: r > R , r = R , r < R. Найдите ускорение этих точек, если ось колеса движется с постоянной скоростью v.
Ответ: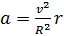 
Задача 42
Луна обращена к Земле постоянно одной стороной. Сколько оборотов совершит она вокруг своей оси за время полного оборота вокруг Земли?
Ответ: простой
Задача 43
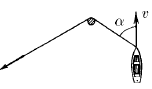Веревку, привязанную к лодке, тянут за свободный конец таким образом, чтобы она не провисала. Лодка движется с постоянной скоростью v, образуя в некоторый момент времени угол α с отрезком веревки, находящимся между столбом и лодкой. С какой скоростью нужно тянуть в этот момент времени свободный конец веревки?
Ответ: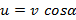 
Задача 44
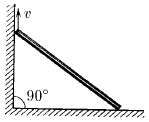
Стержень длины L упирается своими концами в стороны прямого угла. Верхний конец стержня поднимают со скоростью v. Найдите, как зависит от времени скорость его нижнего конца. Начало отсчета времени считать моментом, когда верхний конец стержня находится в вершине прямого угла.
Ответ: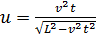 
Задача 45
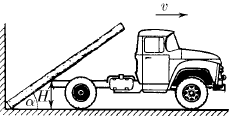
Бревно, упираясь нижним своим концом в угол между стеной и землей, касается дна грузовика на высоте H от земли. Найдите угловую скорость бревна в зависимости от угла α между ним и горизонтом, если грузовик отъезжает от стены со скоростью v.
Ответ: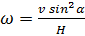 
Динамика.
Законы Ньютона.
Задача 46
Шайба, скользившая по льду, остановилась через время t = 5 с после удара о клюшку на расстоянии l = 20 м от места удара. Масса шайбы m = 100 г. Определите действовавшую на шайбу силу трения.
Ответ: 16Н
Задача 47
Два тела массы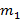 
и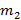 
связаны нитью, выдерживающей силу натяжения T. К телам приложены силы 
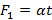и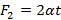 
, где α – постоянный коэффициент, а t – время действия силы. Определите, в какой момент времени нить порвется.
Ответ: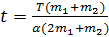 
Задача 48
Для подготовки к работе в условиях невесомости одетые в скафандры космонавты тренируются в воде. При этом сила тяжести, действующая на них, уравновешивается выталкивающей силой. В чем отличие такой «невесомости» от настоящей?
Ответ: тут думать надо
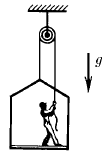Задача 49
Маляр работает в подвесной люльке. Ему понадобилось срочно подняться вверх. Он начинает тянуть за веревку с такой силой, что сила его давления на пол люльки уменьшилась до 400 Н. Масса люльки 12 кг. Масса маляра 72 кг. Чему равно ускорение люльки?
Ответ: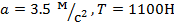 
Задача 50
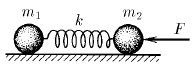Тела массы 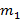и 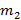соединены пружиной жесткости k. На тело массы 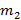действует постоянная сила F, направленная вдоль пружины к телу массы 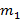. Найдите на сколько сжата пружина, если никаких других внешних сил нет, а колебания уже прекратились. Каким будет ускорение тел сразу же после прекращения действия силы F?
Ответ: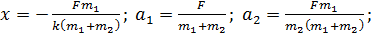 
Задача 51
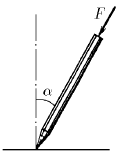Если нажимать пальцем на шариковую ручку, опирающуюся на твердую поверхность, одновременно наклоняя ее, то, пока ручка образует малый угол с перпендикуляром к поверхности, она будет следовать за пальцем (как шарнирно закрепленная). Как только угол наклона достигнет какого-то значения 
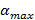, она выскользнет из-под пальца, независимо от приложенной силы. Поэкспериментируйте и оцените коэффициент трения между шариком ручки и поверхностью, на которую она опирается.
Ответ: это ваш эксперимент
Задача 52
На горизонтальной доске лежит брусок массы m. Доску медленно наклоняют. Определите зависимость силы трения действующей на брусок, от угла наклона доски α. Коэффициент трения μ.
Ответ:
Задача 53
Через какое время скорость тела, которому сообщили вверх по наклонной плоскости скорость v, снова будет равна v? Коэффициент трения μ, угол между плоскостью и горизонтом α.
Ответ: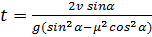 
Задача 54
На тело массы m, лежащее на горизонтальной плоскости, действует сила F под углом α к горизонту. Коэффициент трения μ. Найдите ускорение тела, если оно не отрывается от плоскости.
Ответ: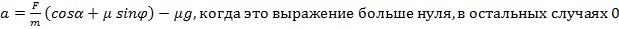 
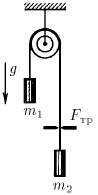Задача 55
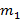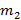Нить, перекинутая через блок с неподвижной осью, пропущена через щель. На концах нити подвешены грузы, масса которых и . Определите ускорения грузов, если при движении нити на нее со стороны щели действует постоянная сила трения 
.
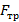Ответ: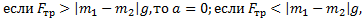 
Задача 56
Коэффициент трения шипованных шин на обледеневшей дороге в десять раз больше чем нешипованных. Во сколько раз нужно занижать скорость движения, чтобы длина тормозного пути оставалась прежней?
Ответ: готовьтесь к взрослой жизни, будущие водители=)
Задача 57
Спортивный автомобиль, трогаясь с места разгоняется до 72 км/ч за 5 с (быстрее невозможно в силу проскальзывания колес). Каков коэффициент трения между колесами и дорогой? Каким будет наименьший тормозной путь данного автомобиля при торможении с той же скорости?
Ответ: а вдруг вы купите спорткар?
Задача 58
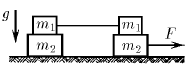На гладком горизонтальном столе расположена система грузов, изображенная на рисунке. Правый нижний груз тянут вдоль стола с силой F, как указано на рисунке. Коэффициент трения между грузами массы 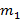и 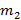равен μ. Найдите ускорение всех грузов системы.
Ответ: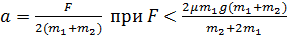 
Задача 59
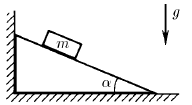Определите силу действующую на вертикальную стенку со стороны клина, если на него положили груз массы m. Угол при основании клина α. Коэффициент трения между грузом и клином μ. Трения между клином и полом нет.
Ответ: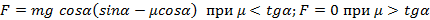 
Задача 60
Сила сопротивления воздуха действующая на велосипедиста пропорциональна квадрату скорости велосипедиста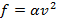 
. На горизонтальной дороге наибольшая скорость велосипедиста составляет примерно 20 м/с. Оцените коэффициент пропорциональности α, если масса велосипедиста вместе с велосипедом 70 кг, а коэффициент трения между колесами и дорогой 0,4.
Ответ: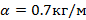 
Задача 61
Сила сопротивления жидкости или газа, пропорциональная квадрату скорости движущегося теля, связана с образованием вихрей вблизи поверхности этого тела. Сила сопротивления, пропорциональная скорости движущегося тела, связана с проскальзыванием слоев среды при обтекании ею этого теля. Оба явления всегда проходят одновременно. Почему тем не менее в тех или иных случаях можно принимать во внимание только один какой-либо вид сопротивления? По данным задач 22 и 23, решенных в классе, оцените, при каком значении произведения радиуса круглой капли на ее скорость оба вида сопротивления воздуха сравнимы по своему воздействию на движение капли.
Задача 62
Электроны, движущиеся по окружности любого радиуса вокруг заряженной нити, имеют одну и ту же скорость v. Масса электрона me. Как зависит сила, действующая со стороны нити на электрон, от расстояния между электроном и нитью? Опишите качественно начальный отрезок траектории, по которой будет двигаться электрон, если скорость его движении по окружности станет вдруг чуть меньше v? Чуть больше v?
Задача 63
Почему крепко засевший в бревне гвоздь проще вытащить, если при этом его вращать вокруг своей оси?
Ответ: потому
Задача 64
По наклонной плоскости скользят два тела одинаковой массы, связанные нитью. Сила натяжения нити T. Трения между одним телом и плоскостью нет. Определите силу трения между доской и другим телом.
Ответ: очевиден
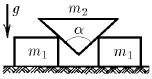Задача 65
Между двумя гладкими брусками массы 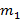каждый вставлен клин массы и 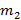с углом раствора α. Определите ускорение всех тел системы. Трения нет
Ответ: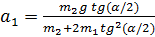 
; 
;
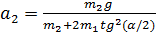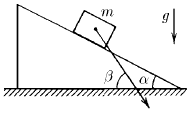Задача 66
На гладкой горизонтальной плоскости находится клин с углом раствора α. Тело массы m, положенное на клин, опускается с ускорением, направленным под углом β > α к горизонту. Определите массу клина.
Ответ: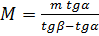 
Задача 67
Ускорение звезд, входящих в состав двойной звезды,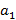 
и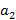 
. Какова масса второй звезды, если масса первой ?
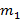Ответ: слишком просто
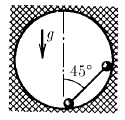
Задача 68
В сферическую полость положили гантель с шариками массы m и невесомым стержнем так, как это показано на рисунке. Определите силу давления шариков на стенки сразу после того, как гантель отпустили. Радиус шариков много меньше радиуса сферы.
Ответ: для верхнего mg/2, для нижнего 3mg/2
Задача 69
Два шарика массы m каждый связаны нитью длины l и движутся со скоростью v по горизонтальному столу в направлении, перпендикулярном связывающей их нити. Нить не провисает. Середина нити налетает на гвоздь вбитый в поверхность стола. Чему равна сила натяжения нити в этот момент?
Ответ: халява
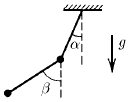
Задача 70
К тяжелому шарику, подвешенному на нити длины l, подвешен другой тяжелый шарик на нити той же длины. При вращении шариков вокруг вертикальной оси, проходящей через верхнюю точку подвеса первого шарика, обе нити лежат в одной плоскости и составляют с вертикалью постоянные углы α и β. Найдите угловую скорость вращения шариков.
Ответ: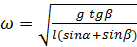 
Задача 71
Груз массы m, прикрепленный пружиной жесткости k к оси, движется вокруг этой оси по окружности радиуса R с угловой скоростью ω. Какова длина недеформированной пружины?
Ответ: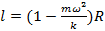 
;
Задача 72
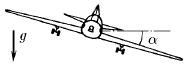Самолет совершает вираж, двигаясь по горизонтальной окружности радиуса R с постоянной скоростью v. Какой угол составляет плоскость крыла самолета с горизонтом?
Ответ: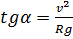 
Задача 73
Горизонтальный диск начинают раскручивать вокруг своей оси с линейно возрастающей по времени угловой скоростью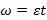 
. При какой угловой скорости тело, расположенное на расстоянии r от оси диска начнет соскальзывать с него, если коэффициент трения между ними равен μ?
Ответ: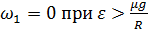 
; 
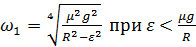
Задача 74
С какой максимальной скоростью может ехать по горизонтальной плоскости мотоциклист, описывая круг радиуса R, если коэффициент трения равен μ? На какой угол от вертикали он должен при этом отклониться? Во сколько раз увеличится максимально допустимая скорость мотоциклиста при движении по наклонному треку с углом наклона α к горизонту по сравнению с максимально допустимой скоростью при движении по горизонтальному треку при том же радиусе поворота и том же коэффициенте трения.
Ответ: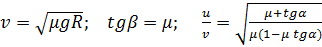 
Импульс. Центр масс.
Задача 75
Первоначально неподвижное тело, находящееся на горизонтальной плоскости, начали тянуть за привязанную к нему веревку с постоянной горизонтальной силой F. Через время Δt действие силы прекратилось. Какая сила трения действовала на тело во время его движения, если оно остановилось спустя время 3Δ t после начала движения?
Ответ: F тр = F /3
Задача 76
Космический корабль должен, изменив курс, двигаться с прежним по модулю импульсом p под углом α к первоначальному направлению. На какое наименьшее время нужно включить двигатель с силой тяги F и как при этом ориентировать ось двигателя?
Ответ: t = 2 pSin ( α /2)/ F , β = (π+α)/2
Задача 77
Сестры стоят на коньках на гладком льду. Старшая толкает младшую. Обе начинают катиться, но младшая с заметно большей скоростью, чем старшая. «Давай, теперь я тебя толкну», говорит младшая. Вопреки ее ожиданиям, она снова откатывается с большей скоростью, чем ее старшая сестра, причем во столько же большей, как в первый раз. Почему так происходит?
Задача 78
Человек решил бежать по резиновой ленте горизонтального транспортера, которая натянута на ролики, трения в осях которых нет. Останется ли человек на месте или будет двигаться относительно земли?
Задача 79
Снаряд разорвался в наивысшей точке траектории своего полета на расстоянии L по горизонтали от пушки на два одинаковых осколка. Один из них вернулся обратно по первоначальной траектории снаряда. Где упал второй осколок?
Ответ: 4 L
Задача 80
Артиллерист стреляет из пушки ядром массы m так, чтобы оно упало на неприятельский лагерь. На вылетевшее из пушки ядро садится барон Мюнхаузен, масса которого 5 m. Какую часть пути до неприятельского лагеря ему придется идти пешком?
Ответ: S / L = 35/36
Задача 81
Частица массы m 1, имеющая скорость v, налетела на покоящееся тело массы m 2 и отскочила от него со скоростью u под прямым углом к направлению первоначального движения. Какова скорость тела массы m 2?
Ответ: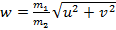 
Задача 82
Радиоактивное ядро распалось на три осколка массы m 1 , m 2 , m 3 имеющих взаимно перпендикулярные скорости v 1 , v 2 , v 3 соответственно. Какова была скорость ядра до распада?
Ответ: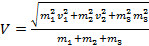 
Задача 83
Космонавт массы m 1 приближается к космическому кораблю массы m 2, с помощью легкого троса. Первоначально корабль и космонавт неподвижны, а расстояние между ними l. Какое расстояние пройдут корабль и космонавт до встречи?
Ответ: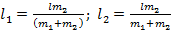 
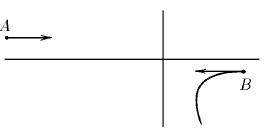Задача 84
Две заряженные частицы массы m и 2 m, имеющие равные по модулю импульсы, одновременно вылетают навстречу друг другу из точек A и B . Частицы взаимодействуют только друг с другом. По траектории частицы массы 2 m восстановите траекторию другой частицы.
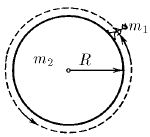
Задача 85
Космическая станция представляет собой цилиндр радиуса R и массы m 2. Космонавт массы m 1 начал круговой обход станции по ее поверхности. Определите траекторию космонавта и траекторию центра станции. В начальный момент времени космонавт и станция неподвижны.
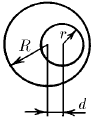
Задача 86
Где находится центр масс произвольной однородной трапеции? однородного круглого гардеробного номерка в виде диска с круглым не концентрическим отверстием (см. рис.)?
Задача 87
Для создания искусственной силы тяжести два отсека орбитальной станции (отношение масс 1:2) развели на расстояние R друг от друга и раскрутили вокруг их общего центра масс. Определите время полного оборота отсеков, если в более массивном отсеке искусственная сила тяжести в два раза меньше силы тяжести на Земле.
Ответ: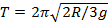 
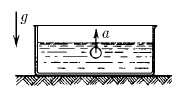Задача 88
В сосуде, наполненном водой плотности ρ, с ускорением a всплывает пузырек воздуха, объем которого V. Найдите силу давления со стороны сосуда на опору. Масса сосуда вместе с водой равна m.
Ответ: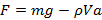 
Задача 89
На чаше весов прыгает N шариков массы m каждый. Какова средняя сила, действующая на чашу весов, если скорость шариков по модулю не меняется? Увеличивается или уменьшается эта сила, если после удара скорость каждого шарика будет уменьшаться?
Ответ: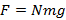 
Задача 90
На чаше весов стоят песочные часы. Когда песок внизу, показания весов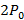 
. Вес песка равен 
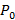. Часы переворачивают. Нарисуйте график зависимости показания весов от времени. Время падения каждой песчинки Δt, время протекания песка T.
Задача 91
С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально вверх со скоростью v? Масса змеи m, ее длина l.
Ответ: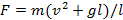 
Дата: 2018-12-21, просмотров: 380.
