Пусть т. М0- критическая, причем
z=f(x,y)- непрерывна в т. М0
существуют f''xx, f''yy, f''xy в т. М0,
тогда при D(M0)=f''xx(M0)f''yy(M0)-[f''xy(M0)]2 >0, экстремум есть, причем при f''x(M0)<0- максимум, f''yy(M0)>0- минимум.
Если же D<0, экстремума нет, при D=0- ничего нельзя сказать о наличии экстремума.
Пример:
z=x2+y2 Þ 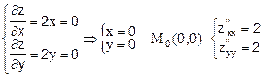
Так как D(М0)=2×2-0>0- экстремум есть, причем z''xx>0 Þ в точке М0-минимум.
Если требуется найти экстремум функции z=f(x,y) при условии, что переменные x,y связаны условием g(x,y)=0, то задачи такого вида называют задачами на условный экстремум и решают методом множителей Лангража.
Метод множителей Лагранжа.
Пусть требуется найти условный экстремум функции z=f(x,y)
при наличии условия g(x,y)=0.
Идея метода Лагранжа состоит в том, что:
1. Вводится новая функция трех переменных, называемая функцией Лангража как F(x,y,l)=f(x,y)+lg(x,y),
где l- неопределенный множитель, который рассматривается как новая переменная;
2. Ищется экстремум (уже безусловный) этой функции. Для этого вычисляются частные производные первого порядка и приравниваются к нулю:
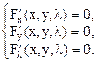
Полученные уравнения образуют систему трех уравнений с тремя неизвестными. Решение этой системы представляет собой тройку чисел (x0, y0, l0), первые два из которых, т. е. (x0,y0), и дают координаты точки условного экстремума исходной функции f(x,y).
Применим метод Лагранжа для отыскания экстремума функций [1].
Пример:
Пусть f(x,y)=x2-3xy+12x при условии g(x,y)=6-2x-3y=0.
Функция Лангража имеет вид F(x,y,l)=x2 - 3xy+12x+l(2x+3y-6).
Тогда F'x(x,y,l)=2x-3y+12+2l,
F'y(x,y,l)=-3x+3l,
F'l(x,y,l)=-6+2x+3y=0.
Приравняв к нулю получим систему
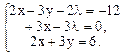
Решим полученную систему методом исключения. Для этого умножим первое (сверху) уравнение на 3, а второе на -2 и складываем, третье уравнение вычитаем из первого. Этим исключается переменная х и система принимает вид:
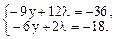
Теперь исключаем переменную l, умножая второе уравнение на -6, и складывая с первым. В результате
-27y=72ÞY=8/3.
Подставляя это значение в уравнение, находим сначала l, затем х:
l=-1; x=-1.
Значит координаты точки условного экстремума (-1, 8/3). Соответствующее значение функции
f(-1, 8/3)=(-1)2×-3×(-1)×(8/3)+12×(-1)=-3.
4. Расчетное задание
Задание 1. Даны матрицы  Найти определитель матрицы
Найти определитель матрицы 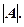 Вычислить результирующую матрицу
Вычислить результирующую матрицу 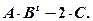
1.1 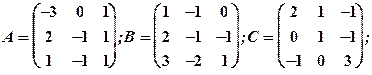
1.2 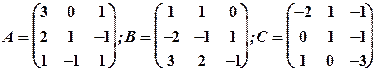
1.3 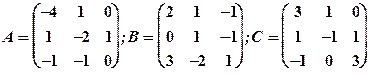
1.4 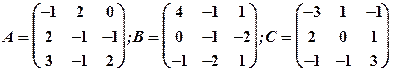
1.5 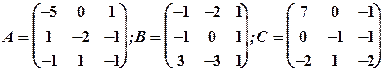
1.6 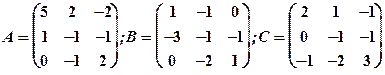
1.7 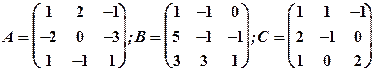
1.8 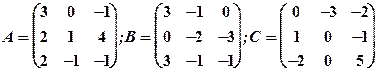
1.9 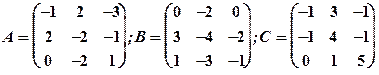
1.10 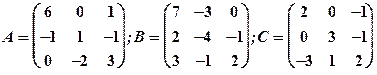
1.11 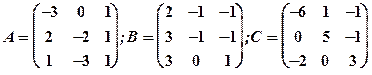
1.12 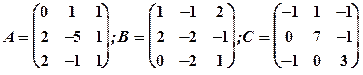
1.13 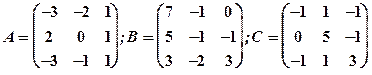
1.14 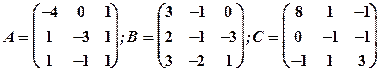
1.15 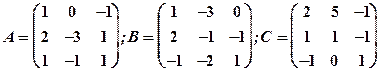
1.16 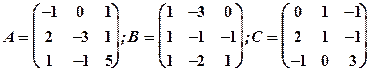
1.17 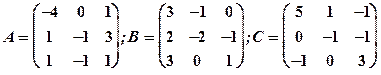
1.18 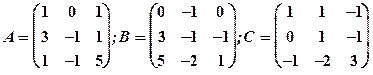
1.19 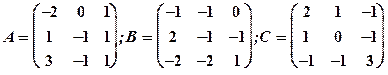
1.20 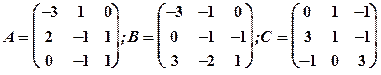
1.21 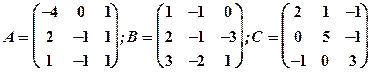
1.22 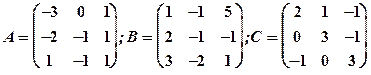
1.23 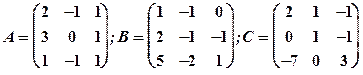
1.24 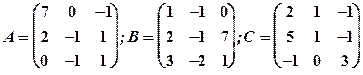
1.25 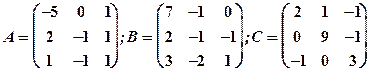
1.26 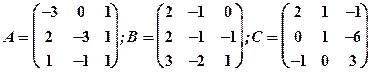
1.27 
1.28 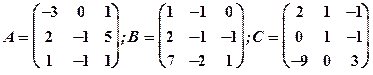
1.29 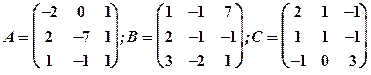
1.30 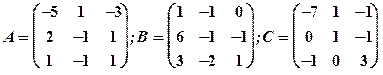
1.31 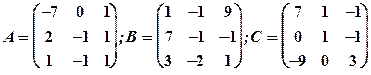
1.32 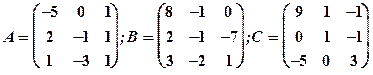
Задание 2. Решить методом Гаусса и как матричное уравнение следующую систему линейных уравнений.
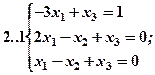
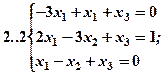
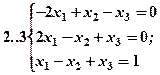
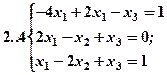
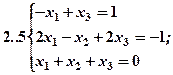
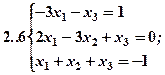
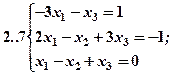
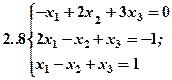
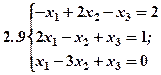
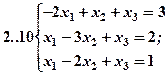
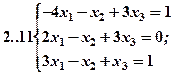
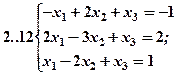
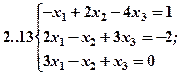
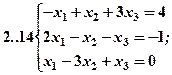
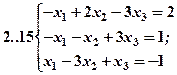
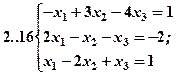
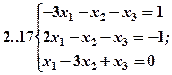
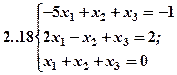
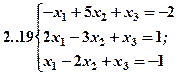
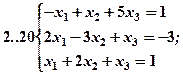
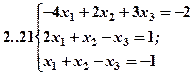
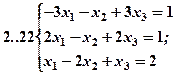
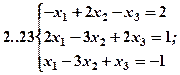
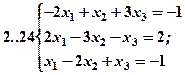
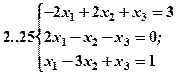
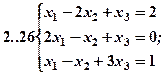
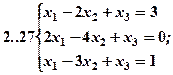
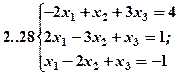
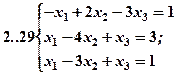
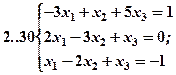

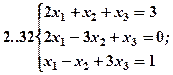
Задание 3. Треугольник ABC задан координатами его вершин: A(-2,1,3), B(1,-2,-3), C(2,-3,-1).
Найти
1). Площадь треугольника ABC;
2). Косинусы углов треугольника;
3). Высоту, опущенную из вершины А на сторону ВС;
4). Определить, параллелен ли вектор 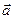 плоскости треугольника АВС.
плоскости треугольника АВС.
Условия задач.
3.1 A(-2,1,4), B(-1,-2,-3), C(3,-3,-1), 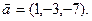
3.2 A(0,3,5), B(1,-2,-3), C(2,-3,-1) 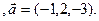
3.3 A(-2,1,3), B(3,-2,-4), C(2,-3,-1) 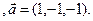
3.4 A(-2,4,3), B(-1,-2,-3), C(2,-3,-1) 
3.5 A(-2,1,3), B(5,-2,-3), C(2,-3,-1) 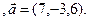
3.6 A(-2,1,3), B(1,-2,-3), C(6,-3,-1) 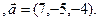
3.7 A(-2,1,4), B(1,-2,-3), C(2,-3,-1) 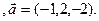
3.8 A(-2,-5,3), B(1,-2,-3), C(2,-3,-1) 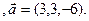
3.9 A(-2,1,3), B(1,-2,-3), C(-2,-3,-1) 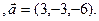
3.10 A(-2,-2,3), B(1,-2,-3), C(2,-3,-1) 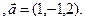
3.11 A(-2,1,3), B(1,-2,-3), C(8,-3,-1) 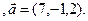
3.12 A(-2,1,3), B(1,-2,-3), C(3,-3,-1) 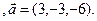
3.13 A(-2,1,5), B(1,-2,-3), C(2,-3,-1) 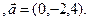
3.14 A(-2,7,3), B(1,-2,-3), C(2,-3,-1) 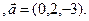
3.15 A(-2,1,3), B(1,-2,-3), C(2,-3,-5) 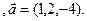
3.16 A(-2,1,3), B(1,-2,3), C(2,-3,-5) 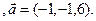
3.17 A(-2,1,3), B(1,-2,-3), C(-3,-3,-1) 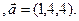
3.18 A(-2,4,3), B(1,-2,-3), C(2,-3,-1) 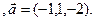
3.19 A(-2,5,3), B(1,-2,-3), C(2,-3,-1) 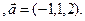
3.20 A(-2,7,3), B(1,-2,-3), C(2,-3,-1) 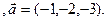
3.21 A(-2,1,-3), B(1,-2,-3), C(2,-3,-1) 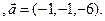
3.22 A(-2,1,3), B(1,-2,-3), C(5,-3,-1) 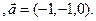
3.23 A(-2,1,3), B(1,-2,-3), C(7,-3,-1) 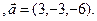
3.24 A(-2,1,5), B(1,-2,-3), C(2,-3,-1) 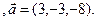
3.25 A(-2,1,1), B(1,-2,-3), C(5,-3,-1) 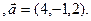
3.26 A(-2,1,-3), B(1,-2,-3), C(5,-3,-1) 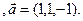
3.27 A(-2,1,-3), B(1,-5,-3), C(2,-3,-1) 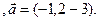
3.28 A(-2,1,5), B(1,-2,-3), C(3,-3,-1) 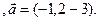 .
.
3.29 A(-2,1,3), B(-1,-2,-3), C(2,-7,-1) 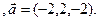
3.30 A(-2,5,3), B(1,-2,-3), C(7,-3,-1) 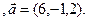
3.31 A(-2,1,1), B(5,-2,-3), C(2,-3,-1) 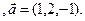
3.32 A(-2,0,3), B(1,-2,-3), C(5,-3,-1) 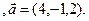
Задание 4. Задана прямая 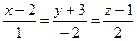 и плоскость
и плоскость 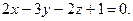
Найти
1). Угол между прямой и плоскостью в градусах, округлив результат до единиц градусов;
2). Точку пересечения прямой и плоскости, если она существует.
4.1 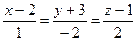 ,
, 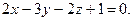
4.2 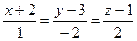 ,
, 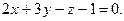
4.3 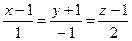 ,
, 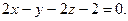
4.4 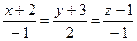 ,
, 
4.5 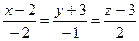 ,
, 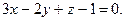
4.6 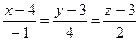 ,
, 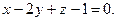
4.7 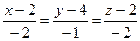 ,
, 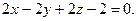
4.8 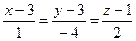 ,
, 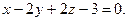
4.9 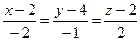 ,
, 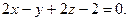
4.10  ,
, 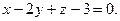
4.11 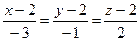 ,
, 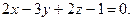
4.12 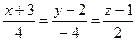 ,
, 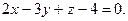
4.13 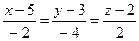 ,
, 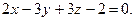
4.14 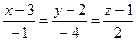 ,
, 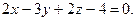
4.15 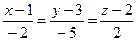 ,
, 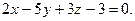
4.16 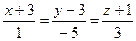 ,
, 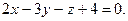
4.17 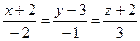 ,
, 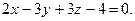
4.18 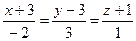 ,
, 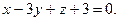
4.19 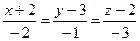 ,
, 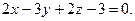
4.20 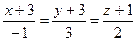 ,
, 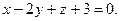
4.21 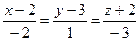 ,
, 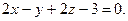
4.22 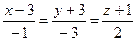 ,
, 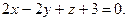
4.23 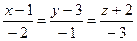 ,
, 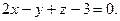
4.24 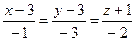 ,
, 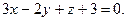
4.25 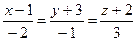 ,
, 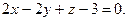
4.26 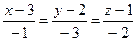 ,
, 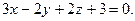
4.27 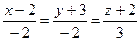 ,
, 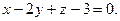
4.28 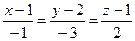 ,
, 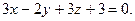
4.29 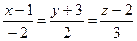 ,
, 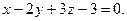
4.30 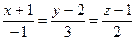 ,
, 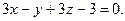
4.31 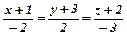 ,
, 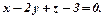
4.32 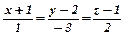 ,
, 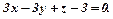
Задание 5. Найти пределы функций.
5.1  ;
; 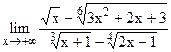 .
.
5.2 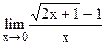 ;
; 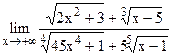 .
.
5.3 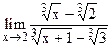 ;
; 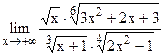 .
.
5.4 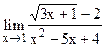 ;
; 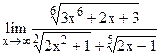 .
.
5.5 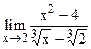 ;
; 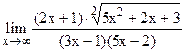 .
.
5.6 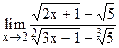 ;
; 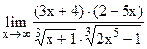 .
.
5.7 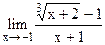 ;
; 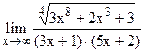 .
.
5.8 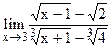 ;
;  .
.
5.9 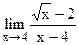 ;
; 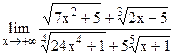 .
.
5.10 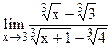 ;
; 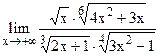 .
.
5.11 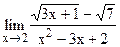 ;
; 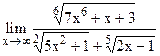 .
.
5.12 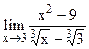 ;
; 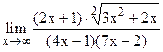 .
.
5.13 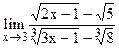 ;
; 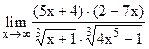 .
.
5.14 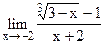 ;
; 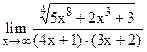 .
.
5.15 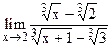 ;
; 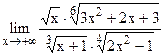 .
.
5.16 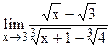 ;
; 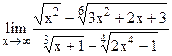
5.17 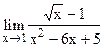 ;
; 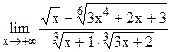
5.18 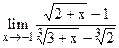 ;
; 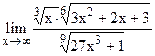
5.19 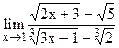 ;
; 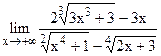
5.20 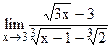 ;
; 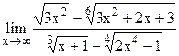
5.21 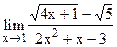 ;
; 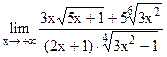
5.22 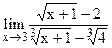 ;
; 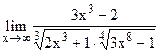
5.23 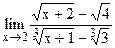 ;
; 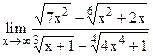
5.24 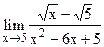 ;
; 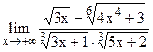
5.25 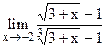 ;
; 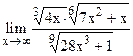
5.26 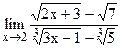 ;
; 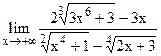
5.27 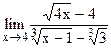 ;
; 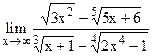
5.28 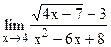 ;
; 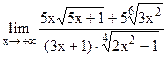
5.29 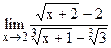 ;
; 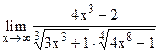
5.30 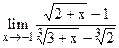 ;
; 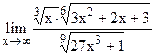
Задание 6. Найти первую производную заданной функции.
6.1 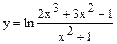 6.2
6.2 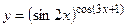
6.3 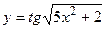 6.4
6.4 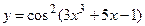
6.5 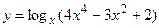
 6.6
6.6 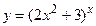
6.7 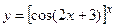 6.8
6.8 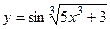
6.9  6.10
6.10 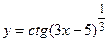
6.11 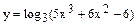 6.12
6.12 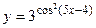
6.13 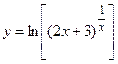 6.14
6.14 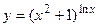
6.15 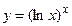 6.16
6.16 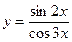
6.17 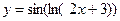 6.18
6.18 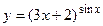
6.19 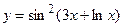 6.20
6.20 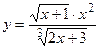
6.21 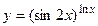 6.22
6.22 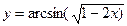
6.23 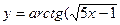 6.24
6.24 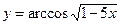
6.25 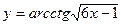 6.26
6.26 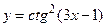
6.27 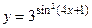 6.28
6.28 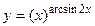
6.29 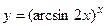 6.30
6.30 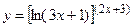
Задание 7. Найти производную указанного порядка при помощи формулы Лейбница.
7.1 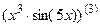 ; 7.2
; 7.2 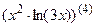 ;
;
7.3 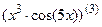 ; 7.4
; 7.4 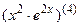 ;
;
7.5 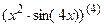 ; 7.6
; 7.6 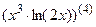 ;
;
7.7 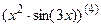 ; 7.8
; 7.8 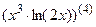 ;
;
7.9 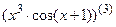 ; 7.10
; 7.10 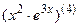 ;
;
7.11 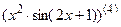 ; 7.12
; 7.12 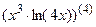 ;
;
7.13 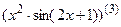 ; 7.14
; 7.14 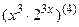 ;
;
7.15 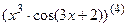 ; 7.16
; 7.16 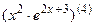 ;
;
7.17 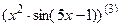 ; 7.18
; 7.18 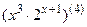 ;
;
7.19 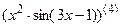 ; 7.20
; 7.20 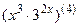 ;
;
7.21 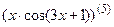 ; 7.22
; 7.22 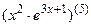 ;
;
7.23 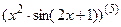 ; 7.24
; 7.24 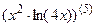 ;
;
7.25 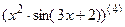 ; 7.26
; 7.26 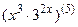 ;
;
7.27 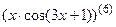 ; 7.28
; 7.28 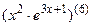 ;
;
7.29 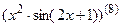 ; 7.30
; 7.30 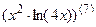 ;
;
Задание 8. Построить график функции при помощи первой производной.
8.1 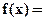
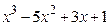 8.2
8.2 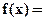
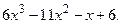
8.3 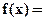
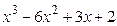 8.4
8.4 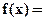
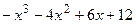
8.5 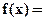
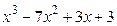 8.6
8.6 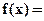
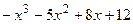
8.7 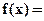
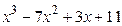 8.8
8.8 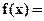
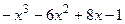
8.9 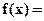
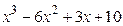 8.10
8.10 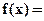
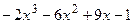
8.11 
 8.12
8.12 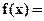
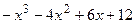
8.13 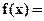
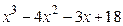 8.14
8.14 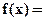
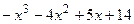
8.15 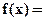
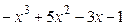 8.16
8.16 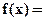
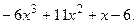
8.17 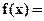
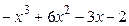 8.18
8.18 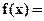
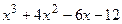
8.19 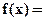
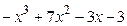 8.20
8.20 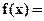
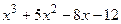
8.21 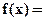
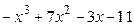 8.22
8.22 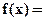
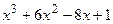
8.23 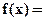
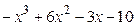 8.24
8.24 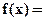
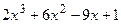
8.25 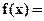
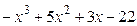 8.26
8.26 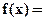
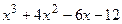
8.27 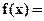
 8.28
8.28 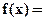
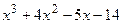
8.29 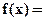
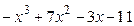 8.30
8.30 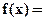
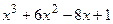
Задание 9. Провести полное исследование функции и построить ее график.
9.1 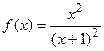 9.2
9.2 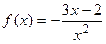
9.3 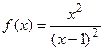 9.4
9.4 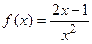
9.5 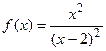 9.6
9.6 
9.7 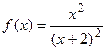 9.8
9.8 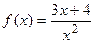
9.9 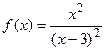 9.10
9.10 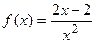
9.11 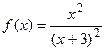 9.12
9.12 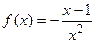
9.13 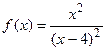 9.14
9.14 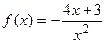
9.15 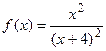 9.16
9.16 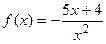
9.17 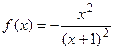 9.18
9.18 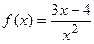
9.19 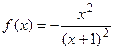 9.20
9.20 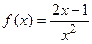
9.21 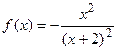 9.22
9.22 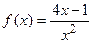
9.23 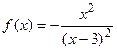 9.24
9.24 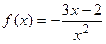
9.25 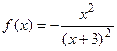 9.26
9.26 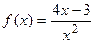
9.27 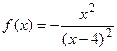 9.28
9.28 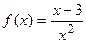
9.29 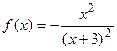 9.30
9.30 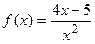
Задание 10. Найти экстремум функции многих переменных в замкнутой области.
10.1 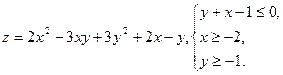
10.2 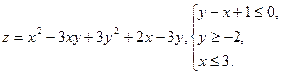
10.3 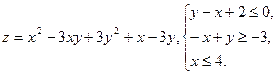
10.4 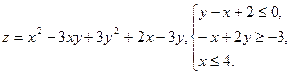
10.5 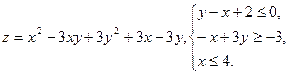
10.6 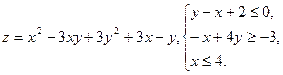
10.7 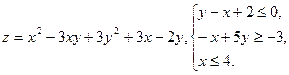
10.8 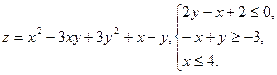
10.9 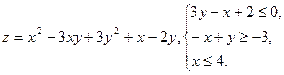
10.10 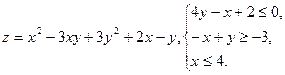
10.11 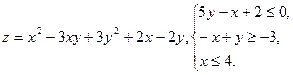
10.12 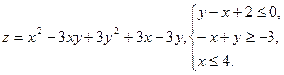
10.13 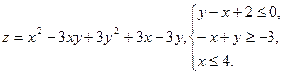
10.14 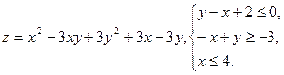
10.15 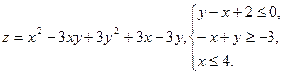
10.16 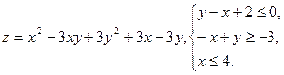
10.17 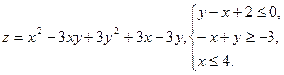
10.18 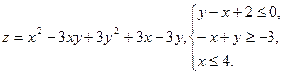
10.19 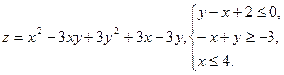
10.20 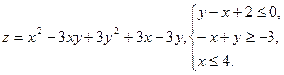
10.21 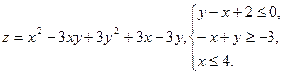
10.22 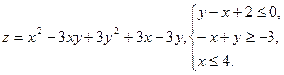
10.23 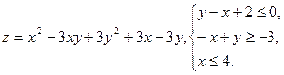
10.24 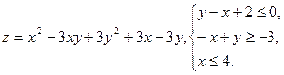
10.25 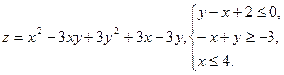
10.26 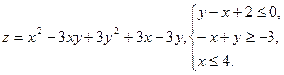
10.27 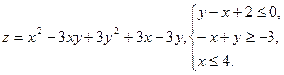
10.28 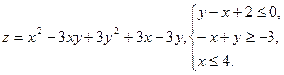
10.29 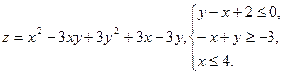
10.30 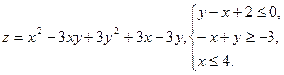
ЛИТЕРАТУРА
1. Шипачев В.С. Высшая математика. Учебник для вузов. М.: Высшая школа, 2005.
2. Письменный Д.Т. Конспект лекций по высшей математике. М.: Айрис-Пресс, 2005.
СОДЕРЖАНИЕ
1. Введение …………………………………………………………………… 3
2. Рекомендации по изучению теоретического материала …………... 4
3. Примеры решения задач ………………………………………………... 7
4. Расчетное задание ……………………………………………………… 39
Литература ………………………………………………………………… 62
Учебно-методическое издание
Денисов Валерий Николаевич
Бобков Владимир Иванович
Выборнова Елена Игоревна
Кулага Николай Филиппович
Математика.
Учебный практикум и контрольные задания
для студентов заочной формы обучения. 1 семестр
Технический редактор М.А. Андреев
Корректор Л.И. Чурлина
__________________________________________________________________________
Подписано в печать 14.10.2010 г.
Формат 60×841/16. Тираж 70 экз. Печ. л. 4. Усл. печ. л. 3,72.
__________________________________________________________________________Издательский сектор филиала ГОУВПО «МЭИ (ТУ)» в г. Смоленске
214013 г. Смоленск, Энергетический проезд, 1
Дата: 2018-12-21, просмотров: 343.