Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Для дифференцируемости функции 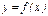  в точке  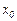необходимо и достаточно, чтобы в точке существовала производная 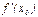. При этом справедлива формула  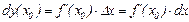, (принято, что ).

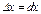Так как уравнение касательной к графику функции в точке 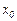   имеет вид

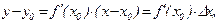
а дифференциал 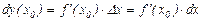, то очевидно, что геометрический смысл дифференциала есть приращение ординаты касательной, проведенной к графику функции  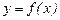в точке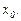

Свойства дифференциала схожи со свойствами производной. Если функции 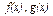дифференцируемы на некотором интервал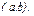е где 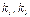- некоторые числа, то

,

 

 

 

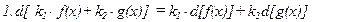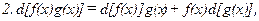
Если функция 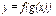сложная, то дифференциал первого порядка обладает свойством инвариантности формы записи (одинаковой формой записи в зависимых и независимых переменных)

 

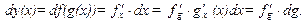
Проиллюстрируем понятие дифференциала на примерах.

Пример:

Вычислить дифференциал функции .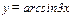

 

Пример:

Найти приближенное значение корня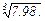  

Рассмотрим функцию 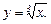 Так как она дифференцируема в точке 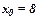, то ее приращение представимо в виде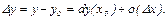

Отбросив бесконечно-малые величины, получим приближенное равенство

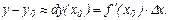
Если 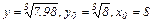, то 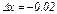, и имеем формулу

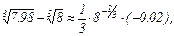
 откуда получаем

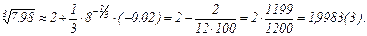
Задание 7. Нахождение производных высших порядков.

Если у функции 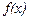существует производная на интервале 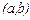, то она в свою очередь является некоторой функцией от .

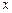Пример:

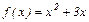,тогда 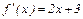; 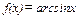, тогда .

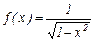Для полученных при дифференцировании функций можно вновь применить понятие производной.

Определение:.

Если на интервале 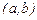 существует производная от первой производной функции  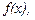то она называется второй производной от 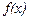на интервале  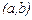и обозначается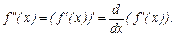  

Пример:

Найти вторую производную функции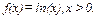

Так как 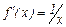, то .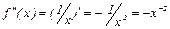

Аналогично можно ввести производные более высокого порядка.

Определение:

Пусть у функции 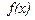существует производная порядка "n-1" на интервале 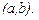Если на этом интервале существует производная от производной порядка " n-1" функции  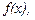то она называется производной порядка "n" и обозначается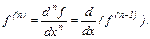  

Пример:

Найти пятую производную функции 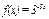. Производя последовательные дифференцирования, имеем

 

,

 

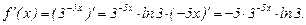
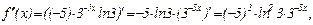
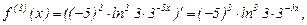
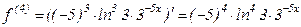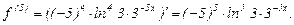
Здесь принято, что производные до второго порядка включительно обозначаются штрихами, производные более высокого порядка обозначаются верхним индексом в скобках. Очевидно, что для нахождения производных высоких порядков нужно последовательно применить первую производную к функции, ее первой производной, второй производной и так до производной нужного порядка.

Заметим, что если существует производная порядка "n", то все производные более низких порядков также существуют. Обратное неверно.

Пусть на интервале ( 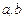 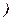существуют производные порядка "n" у функци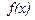й  и 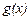 тогда справедливы свойства:

 

1.Линейность.

,

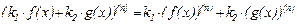где 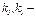 константы. 

 

2.Формула Лейбница

 

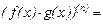
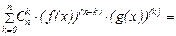
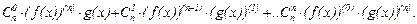
Здесь принято, что знак 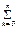- обозначает сумму "n+1" слагаемых, получающихся при изменении индекса  от нуля до "n", а числа 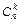   вычисляются по формуле:

 = .

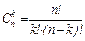Пример:

Вычислить пятую производную 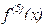, если .

 

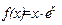Используя формулу Лейбница, имеем:

 

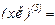
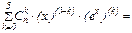
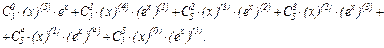
Так как 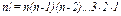, в частности 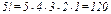, то

 

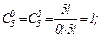
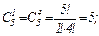
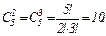
Найдем производные функци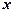й  и , производя последовательные дифференцирования:

    

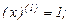
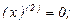
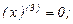
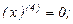
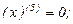
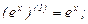
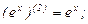
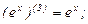
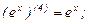
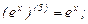
Подставляя найденные производные и числа в формулу Лейбница, получаем:

=

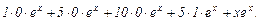
После преобразования имеем:

= .

 

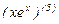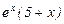Задания 8, 9. Построить график функции.

Полное исследование функции 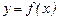 и построение ее графика рекомендуется проводить по схеме:

1. Найти область определения функции D ( x )– множество значений аргумента, при которых функция имеет смысл.

2. Исследовать функцию на периодичность, четность и нечетность.

Если 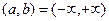 и существует такое числ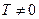о , что для любого 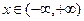, то исследуемая функция периодична с периодом 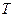. При этом достаточно построить график функции на промежутке  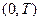и доопределить его по периодичности на всю числовую ось.

Если 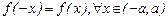, то исследуемая функция четная, в этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке  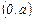 и отобразить его симметрично относительно оси ординат на .

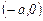Если 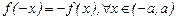, то исследуемая функция нечетная, в этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке 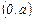и отобразить его симметрично относительно начала координат на .

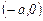3.  Асимптоты. Для их нахождения установить характер точек разрыва функции (если они имеются), исследовать поведение функции в точках разрыва и при 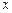 стремящемся к бесконечности.

Если в точке 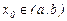  функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту  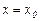(прямая называется асимптотой кривой, если расстояние от точки кривой до этой прямой по мере удаления точки в бесконечность стремится к нулю).

Если при 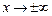 существуют и конечны пределы  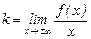и 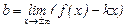, то прямые вида  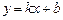называются наклонными асимптотами графика функции .

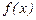4.  Найти экстремумы функции (max или min) и интервалымонотонности функции (возрастания, убывания).

Если на (а, b) производная 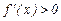, то функция  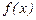возрастает на этом интервале, при  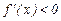функция  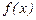 на интервале убывает.

Для отыскания точек экстремума применим следующие приемы:

1) Если в окрестности критической точки первой производной х₀ (эти точки ищут из условий: y' не существует или y'=0) первая производная функции непрерывной функции меняет знак, то в точке 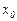 есть экстремум, причем при смене знака производной с “-” на “+” в точке  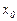имеется минимум( f ( x ₀ )= f_min ) при смене знака с “+” на “-” в точке  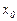имеется максимум( f ( x ₀ )= f_max ).

2) Если в критической точке 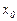 производная 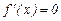, но вторая производная 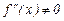, то точка  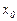- точка экстремума, при этом при значении  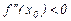в точке  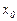имеется максимум ( f ( x ₀ )= f_max ),  если же 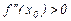, то в точке  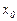имеется минимум( f ( x ₀ )= f_min ).

5. Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.

Для отыскания промежутков выпуклости и вогнутости графика функции применяется вторая производная. Функция 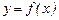 будет выпукла на интервале(выпукла вверх) в том случае, если  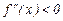на этом интервале, если же  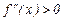  на интервале (а, b ), то функция будет на интервале вогнутой( выпуклой вниз).

Когда в окрестности критической точки х₀  второй производной (эти точки ищут из условий: 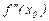 не существует или 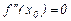) вторая производная функции меняет знак и существует касательная в точке 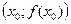_, то точка с координатами  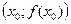 называется точкой перегиба точка перегиба.

6. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график: С осью Оy: положив x =0, и найдя y = f (0). С осью Ох: положив y =0, и решив уравнение. f ( x )=0 ( это уравнение решают только в случае, если оно простое).

7.По результатам исследования по пунктам 1-6 построить график данной функции.

 

Пример:

Построить график функции .

1.  Найдем область определения данной функции.

Данная функция определена и непрерывна на всей числовой оси, кроме точек х= -1 и х=1, т.к. в этих точках функция не определена. Значит точки х= -1 и х=1 - точки разрыва функции:

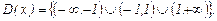
Исследуем данную функцию на четность, нечетность и периодичность.

 

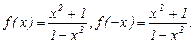
Так как f(-x)=f(x), то данная функция является четной и ее график симметричен относительно оси Оy. Поэтому дальнейшие исследования будем проводить для х 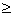0.

Функция не является периодической.

 

1. Исследуем характер точек разрыва функции и поведение функции в бесконечности.

В точках 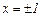  имеем:

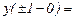
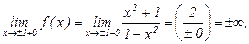
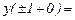
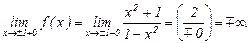
Значит, точки 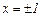 – точки бесконечного разрыва 2 рода.

При 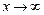  получаем:

_.

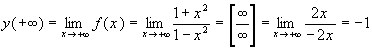Заметим, что при вычислении предела применялось правило Лопиталя):

 

 

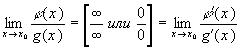
3. Найдем асимптоты графика функции.

а) Вертикальные.

Так как 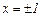 - точки бесконечного разрыва функции, то  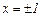– уравнения вертикальных асимптот графика функции .

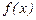б) Наклонные асимптоты ищем в виде .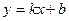

Для правой ветви графика функции имеем:

,

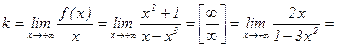
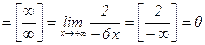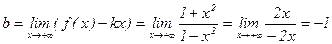
(при вычислениях пределов применялось правило Лопиталя).

Значит, y= -1 – уравнение горизонтальной асимптоты для правой ветви.

 

4. Найдем интервалы монотонности и экстремумы функции.

Вычислим первую производную функции:

.

Найдем теперь критические точки 1 рода из условий первая производная y'=0 или не существует.

y' существует для всех x принадлежащих D(x).

y'=0 при 4x= 0, т.е. x= 0 - критическая точка функции первого рода.

Отметим эту точку на числовой оси и разобьем область определения исследуемой функции ( х 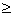0) на интервалы [0; 1) и (1; ):

 

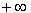Найдем знак y' на каждом из интервалов:

(0; 1): y'(0,5)=4·0,5/(1-0,5²)²=2/(0,75)²>0 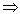функция возрастает на данном интервале.

(1; 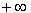): y'(2)=4·2/(1-2²)²=8/9>0 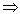функция возрастает на данном интервале.

1. Найдем интервалы выпуклости и вогнутости графика функции и точки перегиба.

Вычислим вторую производную функции:

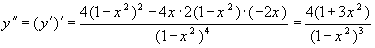
Найдем теперь критические точки 2 рода из условий y" не существует и y"=0.

y" существует для всех x принадлежащих D(x).

y"=0 при 3x²+1=0 - уравнение решений не имеет. Нет критических точек 2 рода.

Отметим на числовой оси область определения функции (х 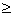0)

 

 

Найдем знак y^" на каждом из интервалов:

(0; 1): y^"(0,5)=4·(1+3·0,5²)/(1-0,5²)³=4·1,75/(0,75)³>0 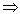направление выпуклости вниз на данном интервале.

(1; 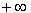): y^"(2)= 4·(1+3·4)/(1-4)³=4·13/(-27)<0 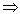направление выпуклости вверх на данном интервале.

Точек перегиба нет.

    

6. Найдем точки пересечения с осями координат. 

 С осью 0у : х=0 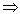y=1; т. пересечения – (0;1)

С осью 0х: у=0 при x² +1=0 – решений не имеет, нет точек пересечения.

7. По результатам исследования по пунктам 1-6 составим таблицу и построим график данной функции для х 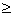0.

х	0	(0;1)	(1; )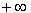
y'	0	+	+
y"		+	-
y	1	Выпукл. вниз возрастает	Выпукл. вверх возрастает
	min

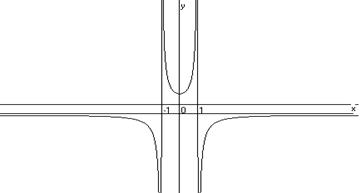
Строим теперь график для х 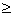0 и отражаем его симметрично относительно оси Оy

                                                   

 

Задание 10. Нахождение частных производных ФМП и исследование на экстремум в замкнутой области.

Функции нескольких переменных: область определения, частные производные. Производные сложных функций

Определение: Функции двух переменных.

Если " упорядоченной паре чисел (x,y)ÎD по некоторому закону f ставится в соответствие число zÎE, то говорят, что задана функция z=f(x,y). Множество D- область определения, а E - область изменения функции.

Геометрический смысл ФМП - поверхность в пространстве.

Пример:

Z=x²+y² задает параболоид, а Z=A₁x+B₁y+D₁ - плоскость.

 

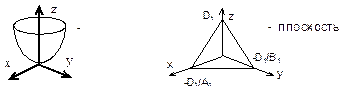
Определение: Функции многих переменных (ФМП.)

Если "(x₁,x₂,...x_n) 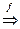zÎR, то говорят, что z=f(x₁,x₂,...x_n)- ФМП.

Пример:

Нахождение областей определения ФМП производят с учетом свойств элементарных функций.Если z=ln(xy) Þ xy>0 Û 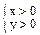 или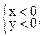    

при z=ln(sin(xy)) Þ sin (xy)>0 Þ 0+2pk<xy<p+2pk.

Пределы ФМП

Определение:

Число А называют пределом ФМП z=f(x,y) в т.(x₀,y₀),если

"e>0 $d>0:"пар (x,y) из неравенства 0<(x-x₀)²+(y-y₀)²<d²

^{следует}                     Þ½f(x,y)-A½<e,

при этом пишут:

.

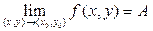Если А=0, т. е. 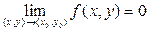, то функцию f(x,y) называют бесконечно-малой ( БМФ ) при (x,y)®(x₀,y₀).

Определение: Бесконечно большой функции.

Если "М>0 $d:"(x,y) из 0<(x- х₀)²+(y-y₀)²<d² Þ ½f(x,y)½>M, при этом пишут 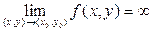 и говорят, что z=f(x,y) бесконечно-большая ( ББФ), при (x,y)®(x₀,y₀).

Геометрический смысл.

 

z=      

 

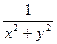
Определение: Непрерывной функции.

Говорят, что функция f(x,y) непрерывна в т. (х₀,y₀), если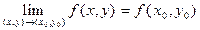

 

Замечание:

Кроме 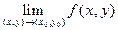существуют повторные пределы  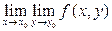и 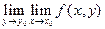, причем из 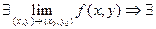- повторных пределов, но из $-я повторных пределов не следует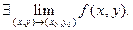

 

Пример:

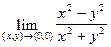-? Найдем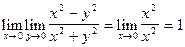

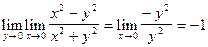
Но предел, если он существует, единственен, значит не существует предела z= , при (x,y)®(0,0).

 

Частные производные ФМП

Пусть z=f(x,y) определена в т. M₀(x₀,y₀) и ее окрестности

Назовем разность x-x₀=Dx- приращением координаты х, а

y-y₀=Dy- приращением координаты y    , тогда для функции z=f(x,y) имеем

D_xz=f(x₀+Dx,y₀)-f(x₀,y₀)- частное приращение по координате x

D_yz=f(x₀,y₀+Dx)-f(x₀,y₀)- частное приращение по координате y.

 

Определение: Частной производной по переменной х.

Если существует конечный предел отношения D_xz к Dх при Dx®0, то он называется частной производной по переменной х и обозначается

 .

 

Определение: Частной производной по переменной у.

 

.

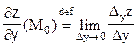При нахождении частной производной по заданной переменной фиксируются все переменные кроме заданной и частная производная находится как обычная производная функции одной переменной.

 

Геометрический смысл частных производных

     

 

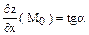
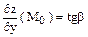
Пример:

z=x^y, 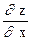=yx^y-1, 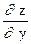=x^y×ln x

z=ln xy, z'_x=1/xy×(xy)'_x=y/xy=1/x.

z'_y=1/xy×(xy)'_y=x/xy=1/y.