39. Понятие о дифференциальном уравнении. Дифференциальные уравнения первого порядка. Понятие об общем и частном решении. Начальные условия. Интегральные кривые.
40. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения. Линейные дифференциальные уравнения.
41. Теорема о существовании и единственности решения дифференциального уравнения первого порядка (без доказательства).
42. Поле направлений дифференциального уравнения. Изоклины. Приближенное решение дифференциальных уравнений первого порядка (способ Эйлера).
43. Линейные однородные дифференциальные уравнения второго порядка. Линейно-независимые решения. Структура общего решения.
44. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение. Общее решение уравнения.
45. Общее решение линейного неоднородного дифференциального уравнения второго порядка. Теорема наложения. Метод вариации произвольных постоянных. Частные решения линейных дифференциальных уравнений второго порядка с постоянными коэффициентами для правых частей в виде функций: многочлен; Aekx ; A 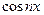 + B
+ B 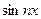 .
.
46. Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами. Системы линейных дифференциальных уравнений с постоянными коэффициентами.
VI . РЯДЫ
47. Числовые ряды; их сходимость и расходимость. Необходимые условия сходимости. Свойства сходящихся рядов.
48. Ряды с положительными членами. Признаки сходимости, основанные на сравнении рядов. Признак Даламбера. Интегральный признак Коши.
49. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.
50. Степенные ряды. Теорема Абеля. Интервал сходимости.
51. Ряды Тейлора и Маклорена. Биноминальный ряд. Разложение в степенной ряд элементарных функций.
52. Приложение степенных рядов к приближенным вычислениям, вычисление определенных интегралов, решение дифференциальных уравнений.
VII . ТЕОРИЯ ВЕРОЯТНОСТЕЙ
53. Вероятность события. Относительная частота события. Полная группа событий. Статистическое и классическое определение вероятности.
54. Сумма событий. Теорема о вероятности суммы несовместных событий. Теорема вероятности суммы двух совместных событий.
55. Произведение событий. Условная вероятность. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса.
56. Теорема о повторении опытов (схема Бернулли). Наивероятнейшая частота при повторении опытов. Биноминальное распределение. Формула Пуассона.
57. Понятие случайной величины. Дискретные и непрерывные случайные величины. Функция распределения случайной величины. Примеры распределений: нормальное, биноминальное, пуассоновское, равномерное. Вероятность попадания случайной величины на данный интервал.
58. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение; их свойства.
59. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева.
60. Числовые характеристики статистических распределений (математическое ожидание, дисперсия). Оценка вероятности по частоте. Понятие о доверительном интервале. Доверительные интервалы для среднего значения и дисперсии нормально распределенной случайной величины.
61. Понятие о центральной предельной теореме.
Дата: 2018-12-21, просмотров: 322.