Российской Федерации
Красноярский государственный аграрный университет
МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ
ЗАДАНИЯ ДЛЯ СТУДЕНТОВ-ЗАОЧНИКОВ
КРАСНОЯРСК 2016
Составитель: Миронов Г.В.
Миронов Г.В. "МАТЕМАТИКА". Методические указания по выполнению контрольных работ и прохождению промежуточного контроля для студентов заочной формы обучения по направлению подготовки Землеустройство и кадастры ‒ бакалавриат 21.03.02 Института ЗКиП. Краснояр. гос. аграр. ун-т.- Красноярск, 2016. с.
Введение
В соответствии с действующими учебным планом студенты-заочники изучают курс высшей математики в течении двух лет и выполняют на каждом курсе по две контрольные работы.
Контрольные работы №1 и №2 выполняются студентами на первом курсе.
Контрольные работы №3 и №4 выполняются на втором курсе.
При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Каждая работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр, номер контрольной работы.
2. Контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условие.
3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем.
4. Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единицей измерения. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах.
5. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
6. Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме.
Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена
7. Получив из института прорецензированную работу (как зачтенную, так и незачтенную), студент должен исправить все отмеченные рецензентом ошибки и недочеты. В случае незачета по работе студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
8. В межсессионный период или во время лабораторно-экзаменационной сессии студент должен пройти на кафедре высшей математики собеседование по зачтенной контрольной работе.
9. Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра. При этом, если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1. если предпоследняя цифра учебного шифра есть число четное или ноль (2, 4, 6, 8, 0), то номера задач даны в таблице 2.
Таблица 1
| Номер варианта | Номера задач для контрольных работ | |||||||||||||||
|
Работа №1 |
Работа №2 | |||||||||||||||
| 1 | 1 | 21 | 31 | 41 | 51 | 61 | 81 | 101 | 121 | 131 | 141 | 161 | ||||
| 2 | 2 | 22 | 32 | 42 | 52 | 62 | 82 | 102 | 122 | 132 | 142 | 162 | ||||
| 3 | 3 | 23 | 33 | 43 | 53 | 63 | 83 | 103 | 123 | 133 | 143 | 163 | ||||
| 4 | 4 | 24 | 34 | 44 | 54 | 64 | 84 | 104 | 124 | 134 | 144 | 164 | ||||
| 5 | 5 | 25 | 35 | 45 | 55 | 65 | 85 | 105 | 125 | 135 | 145 | 165 | ||||
| 6 | 6 | 26 | 36 | 46 | 56 | 66 | 86 | 106 | 126 | 136 | 146 | 166 | ||||
| 7 | 7 | 27 | 37 | 47 | 57 | 67 | 87 | 107 | 127 | 137 | 147 | 167 | ||||
| 8 | 8 | 28 | 38 | 48 | 58 | 68 | 88 | 108 | 128 | 138 | 148 | 168 | ||||
| 9 | 9 | 29 | 39 | 49 | 59 | 69 | 89 | 109 | 129 | 139 | 149 | 169 | ||||
| 0 | 10 | 30 | 40 | 50 | 60 | 70 | 90 | 110 | 130 | 140 | 150 | 170 | ||||
|
Работа №3 |
Работа №4 | |||||||||||||||
| 1 | 181 | 191 | 201 | 211 | 231 | 251 | 271 | 281 | 291 | 301 | 311 | |||||
| 2 | 182 | 192 | 202 | 212 | 232 | 252 | 272 | 282 | 292 | 302 | 312 | |||||
| 3 | 183 | 193 | 203 | 213 | 233 | 253 | 273 | 283 | 293 | 303 | 313 | |||||
| 4 | 184 | 194 | 204 | 214 | 234 | 254 | 274 | 284 | 294 | 304 | 314 | |||||
| 5 | 185 | 195 | 205 | 215 | 235 | 255 | 275 | 285 | 295 | 305 | 315 | |||||
| 6 | 186 | 196 | 206 | 216 | 236 | 256 | 276 | 286 | 296 | 306 | 316 | |||||
| 7 | 187 | 197 | 207 | 217 | 237 | 257 | 277 | 287 | 297 | 307 | 317 | |||||
| 8 | 188 | 198 | 208 | 218 | 238 | 258 | 278 | 288 | 298 | 308 | 318 | |||||
| 9 | 189 | 199 | 209 | 219 | 239 | 259 | 279 | 289 | 299 | 309 | 319 | |||||
| 0 | 190 | 200 | 210 | 220 | 240 | 260 | 280 | 290 | 300 | 310 | 320 | |||||
Таблица 2
| Номер варианта | Номера задач для контрольных работ | |||||||||||||||
|
Работа №1 |
Работа №2 | |||||||||||||||
| 1 | 11 | 22 | 33 | 44 | 55 | 76 | 91 | 111 | 122 | 133 | 151 | 171 | ||||
| 2 | 12 | 23 | 34 | 45 | 56 | 77 | 92 | 112 | 123 | 134 | 152 | 172 | ||||
| 3 | 13 | 24 | 35 | 46 | 57 | 78 | 93 | 113 | 124 | 135 | 153 | 173 | ||||
| 4 | 14 | 25 | 36 | 47 | 58 | 79 | 94 | 114 | 125 | 136 | 154 | 174 | ||||
| 5 | 15 | 26 | 37 | 48 | 59 | 80 | 95 | 115 | 126 | 137 | 155 | 175 | ||||
| 6 | 16 | 27 | 38 | 49 | 60 | 71 | 96 | 116 | 127 | 138 | 156 | 176 | ||||
| 7 | 17 | 28 | 39 | 50 | 51 | 72 | 97 | 117 | 128 | 139 | 157 | 177 | ||||
| 8 | 18 | 29 | 40 | 41 | 52 | 73 | 98 | 118 | 129 | 140 | 158 | 178 | ||||
| 9 | 19 | 30 | 31 | 42 | 53 | 74 | 99 | 119 | 130 | 131 | 159 | 179 | ||||
| 0 | 20 | 21 | 32 | 43 | 54 | 75 | 100 | 120 | 121 | 132 | 160 | 180 | ||||
|
Работа №3 |
Работа №4 | |||||||||||||||
| 1 | 182 | 193 | 204 | 221 | 241 | 261 | 272 | 283 | 294 | 305 | 316 | |||||
| 2 | 183 | 194 | 205 | 222 | 242 | 262 | 273 | 284 | 295 | 306 | 317 | |||||
| 3 | 184 | 195 | 206 | 223 | 243 | 263 | 274 | 285 | 296 | 307 | 318 | |||||
| 4 | 185 | 196 | 207 | 224 | 244 | 264 | 275 | 286 | 297 | 308 | 319 | |||||
| 5 | 186 | 197 | 208 | 225 | 245 | 265 | 276 | 287 | 298 | 309 | 320 | |||||
| 6 | 187 | 198 | 209 | 226 | 246 | 266 | 277 | 288 | 299 | 310 | 311 | |||||
| 7 | 188 | 199 | 210 | 227 | 247 | 267 | 278 | 289 | 300 | 301 | 312 | |||||
| 8 | 189 | 200 | 201 | 228 | 248 | 268 | 279 | 290 | 291 | 302 | 313 | |||||
| 9 | 190 | 191 | 202 | 229 | 249 | 269 | 280 | 281 | 292 | 303 | 314 | |||||
| 0 | 181 | 192 | 203 | 230 | 250 | 270 | 271 | 282 | 293 | 304 | 315 | |||||
СОДЕРЖАНИЕ ПРОГРАММЫ
II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
IV. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
29. Неопределенный интеграл; его свойства. Таблица основных интегралов.
30. Интегрирование заменой переменной; по частям. Интегрирование рациональных дробей.
31. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл как предел интегральных сумм. Понятие об интегрируемой функции, формулировка теоремы существования. Свойства определенного интеграла. Теорема о среднем.
32. Производная от определенного интеграла по верхнему пределу. Связь между определенным и неопределенным интегралом (формула Ньютона – Лейбница).
33. Вычисление определенных интегралов способом подстановки и по частям. Интегрирование четных и нечетных функций в симметричных пределах.
34. Приближенное вычисление определенных интегралов по формулам прямоугольников, трапеций, Симпсона.
35. Геометрические приложения определенного интеграла: вычисления площадей фигур; объемов тел по площадям сечений и тел вращения; длин дуг кривых; площадей поверхностей вращения. Примеры приложения интеграла к решению простейших задач механики и физики.
36. Несобственные интегралы с бесконечными пределами интегрирования и от неограниченных функций. Примеры сходящихся и расходящихся интегралов.
37. Задачи, приводящие к понятию двойного интеграла. Определение двойного интеграла. Вычисление двойного интеграла. Геометрические приложения двойного интеграла.
38. Понятие о тройном интеграле.
VI . РЯДЫ
47. Числовые ряды; их сходимость и расходимость. Необходимые условия сходимости. Свойства сходящихся рядов.
48. Ряды с положительными членами. Признаки сходимости, основанные на сравнении рядов. Признак Даламбера. Интегральный признак Коши.
49. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.
50. Степенные ряды. Теорема Абеля. Интервал сходимости.
51. Ряды Тейлора и Маклорена. Биноминальный ряд. Разложение в степенной ряд элементарных функций.
52. Приложение степенных рядов к приближенным вычислениям, вычисление определенных интегралов, решение дифференциальных уравнений.
VII . ТЕОРИЯ ВЕРОЯТНОСТЕЙ
53. Вероятность события. Относительная частота события. Полная группа событий. Статистическое и классическое определение вероятности.
54. Сумма событий. Теорема о вероятности суммы несовместных событий. Теорема вероятности суммы двух совместных событий.
55. Произведение событий. Условная вероятность. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса.
56. Теорема о повторении опытов (схема Бернулли). Наивероятнейшая частота при повторении опытов. Биноминальное распределение. Формула Пуассона.
57. Понятие случайной величины. Дискретные и непрерывные случайные величины. Функция распределения случайной величины. Примеры распределений: нормальное, биноминальное, пуассоновское, равномерное. Вероятность попадания случайной величины на данный интервал.
58. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение; их свойства.
59. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева.
60. Числовые характеристики статистических распределений (математическое ожидание, дисперсия). Оценка вероятности по частоте. Понятие о доверительном интервале. Доверительные интервалы для среднего значения и дисперсии нормально распределенной случайной величины.
61. Понятие о центральной предельной теореме.
Библиографический список
1. Ефимов Н.В. Краткий курс аналитической геометрии. М.:Физмат Гиз, 2002.
2. Кудрявцев В.А., Демидович В.П. Краткий курс высшей математики. 6-е изд. М.: Наука, 1986.
3. Минорский В.П, Сборник задач по высшей математике. М.: Наука, 2003.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления: т. 1, 2. М.: Наука, 2001.
5. Сборник задач по математике для вузов. Линейная алгебра и основы математического анализа / Под ред. А.В. Ефимова, Б.П. Демидовича. М.: Наука, 1986.
6. Гмурман В.Е. Теория вероятностей и математическая статистика, М.: Высшая школа, 2003.
7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 2003.
В настоящих методических указаниях приведенные пособия для краткости обозначаются заключенными в квадратные скобки номерами из библиографического списка. Например, запись 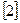 гл. 3;
гл. 3; 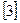 № 66, 68, 81, 113 означает следующее: изучите материал, изложенный в главе 3 учебника Кудрявцева В.А., Демидовича В.П. «Краткий курс высшей математики» и решите задачи № 66, 68, 81, 113 из задачника Минорского В.П.
№ 66, 68, 81, 113 означает следующее: изучите материал, изложенный в главе 3 учебника Кудрявцева В.А., Демидовича В.П. «Краткий курс высшей математики» и решите задачи № 66, 68, 81, 113 из задачника Минорского В.П.
Вопросы для самопроверки
1. Что называется числовым рядом?
2. Что называется n-й частичной суммой числового ряда?
3. Какой числовой ряд называется сходящимся?
4. Что является необходимым условием сходимости числового ряда?
5. Назовите достаточные признаки сходимости, основанные на сравнении рядов.
6. Назовите признак Даламбера сходимости рядов.
7. В чем состоит интегральный признак сходимости Коши?
8. Какие ряды называются знакочередующимися? Приведите примеры.
9. Сформулируйте признак Лейбница сходимости знакочередующихся рядов.
10. Какие знакочередующиеся ряды называются абсолютно сходящимися? Условно сходящимися?
11. Дайте определение степенного ряда и области его сходимости.
12. Как найти область сходимости степенного ряда?
13. Запишите разложение в степенной ряд функций 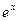 , sin x, cos x,
, sin x, cos x,
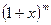 , ln (1+ x ) .
, ln (1+ x ) .
14. Как обеспечивается требуемая точность при применении степенных рядов в приближенных вычислениях?
Характеристики
(6) гл. 6, § 1 – 3, гл. 7, 8, 10, 11;
(7) № 165, 176, 188, 210, 254, 263, 276, 328,341.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 20. Задан закон распределения дискретной случайной величины Х:
Х 40 42 41 44,
Р 0,1 0,3 0,2 0,4.
Найти: 1) математическое ожидание М (Х); 2) дисперсию D (Х); 3) среднее квадратическое отклонение σ.
Решение. 1) Если закон распределения дискретной случайной величины задан таблицей
Х 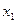
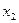 …
… 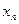
Р 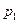
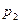
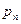 ,
,
где в первой строке даны значения случайной величины Х, а во второй – вероятности этих значений , то математическое ожидание М (Х) вычисляется по формуле
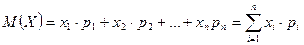 .
.
Тогда M ( X ) = 40 · 0,1 + 42 · 0,3 + 41 · 0,4 = 42,4.
2) Дисперсией D ( X ) дискретной случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.
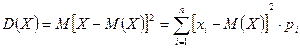 .
.
Эта величина характеризует среднее ожидаемое значение квадрата отклонения X от M (X). Из последней формулы имеем
D ( X ) = ( 40 – 42,4 )²∙0,1+(42 – 42,4)2∙0,3+(41 – 42,4)2∙0,2+
+(44 – 42,4)2∙0,4=2,42∙0,1+0,42∙0,3+1,420,2+1,62∙0,4=
=2,04.
Дисперсия D ( X ) можно найти другим способом, исходя из следующего ее свойства: дисперсия D ( X ) равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания M ( X ), то есть
D ( X) = M ( X ²) - [ M ( X ) ]².
Для вычисления M ( X ²) составим следующий закон распределения величины X ² :
X ² 40² 42² 41² 44²
P 0,1 0,3 0,2 0,4.
Тогда
M ( X ²) = 40² · 0,1 + 42² · 0,3 + 41² · 0,2 + 44² · 0,4 =
= 160 + 529,2 + 336,2 + 774,4 = 1799,8 и
D ( X ) = 1799,8 – 42,4² = 2,04.
3) Для характеристики рассеяния возможных значений случайной величины вокруг его среднего значения вводится среднее квадратическое отклонение σ ( X ) случайной величины X, равное квадратному корню из дисперсии D ( X ), то есть
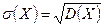 .
.
Из этой формулы имеем: 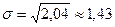 .
.
Задача 21. Непрерывная случайная величина Х задана интегральной функцией распределения
 0 при х < 0,
0 при х < 0,
F (x) = х³ при 0 ≤ х ≤1,
1 при х > 1.
Найти: 1) дифференциальную функцию распределения f ( x ); 2) математическое ожидание M ( X ); 3) дисперсию D ( X ) .
Решение. 1) Дифференциальная функцией распределения f ( x ) непрерывной случайной величины X называется производная от интегральной функции распределения F ( x ) , то есть
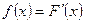 .
.
Искомая дифференциальная функция имеет следующий вид:
 0 при х < 0 ,
0 при х < 0 ,
f (x) = 3 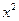 при 0 ≤ х ≤ 1,
при 0 ≤ х ≤ 1,
0 при х > 1.
2) Если непрерывная случайная величина Х задана функцией f ( x ) , то ее математическое ожидание определяется формулой
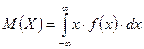 .
.
Так как функция f ( x ) при x < 0 и при x >1 равна нулю, то из последней формулы имеем
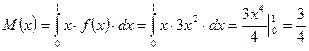 .
.
3) Дисперсию D (X) определим по формуле
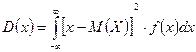 .
.
Тогда
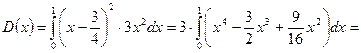
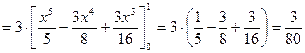 .
.
Задача 22. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 40мм и средним квадратическим отклонением 3мм.Найти:1) вероятность того, что длина детали отклонится от ее математического ожидания не более чем 1,5мм.
Решение: 1) Пусть Х - длина детали. Если случайная величина Х задана дифференциальной функцией f (х), то вероятность того, что Х примет значения, принадлежащие отрезку [α ; β ] , определяется по формуле
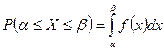 .
.
Вероятность выполнения строгих неравенств L < X < B определяется той же формулой. Если случайная величина Х распределена по нормальному закону, то
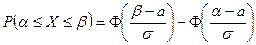 , (1)
, (1)
где Ф (х ) – функция Лапласа, a =M (X), σ = 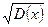 .
.
В задаче а = 40, α = 34, β = 43, σ = 3. Тогда
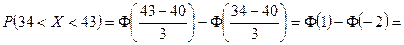
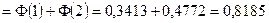 .
.
2) По условию задачи а – δ < Х < а + δ, где а = 40; δ = 1,5. Подставив в (1) α = а – δ, β = а + δ, имеем
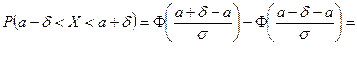
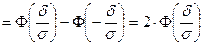 , то есть
, то есть
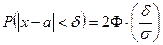 (2)
(2)
Из формулы (2) имеем:
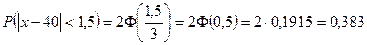 .
.
Вопросы для самопроверки
1. Какие случайные величины называются дискретными? непрерывными? Приведите примеры.
2. Что называется законом распределения случайной величины? Как задается закон распределения дискретной случайной величины?
3. Что называется математическим ожиданием дискретной случайной величины? ее дисперсия? средним квадратическим отклонением? Перечислите их свойства.
4. Дайте определение интегральной функции распределения; дифференциальной функции распределения. Перечислите свойства этих функций.
5. Как вычисляются математическое ожидание и дисперсия непрерывной случайной величины?
6. Напишите дифференциальную функцию для нормального закона распределения.
7. Напишите формулу для определения вероятности попадания значений нормально распределенной случайной величины в заданной интервал.
8. сформулируйте правило « трех сигм ».
9. Назовите сущность закона больших чисел.
10. Напишите неравенство Чебышева.
11. Сформулируйте теорему Чебышева; теорему Бернулли.
Тема 14. Элементы линейного программирования
[2] гл. XXVI § 3.
Задача 23. Предприятие имеет возможность приобрести не более 20 трехтонных и не более 18 пятитонных автомашин. Отпускная цена трехтонного грузовика 4000 у.е, пятитонного – 5000 у.е. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной, если для приобретения автомашин выделено 150 тысяч рублей? Задачу решить графическим и аналитическим методами.
Решение. Пусть приобретено 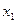 трехтонных и
трехтонных и 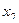 пятитонных
пятитонных
автомашин. Из условия задачи имеем

0 ≤ 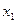 ≤ 20
≤ 20
0 ≤ 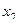 ≤ 18
≤ 18
4 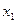 + 5
+ 5 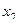 = 150 . (1)
= 150 . (1)
Суммарная грузоподъемность приобретенных грузовиков равна
L = 3 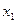 + 5
+ 5 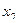 . (2)
. (2)
Задача состоит в нахождении такого решения системы (1) , при котором линейная форма (целевая функция) (2) принимает наибольшее значение.
Графический метод решения
В прямоугольной системе координат 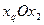 построим многоугольник
построим многоугольник
OABCD, образованный прямыми 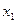 = 0 (OD),
= 0 (OD), 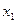 =20 (AB),
=20 (AB), 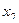 = 0 (AO ),
= 0 (AO ), 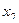 = 18 ( CD), 4
= 18 ( CD), 4 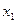 + 5
+ 5 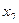 = 150 ( BC) и прямую 3
= 150 ( BC) и прямую 3 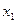 + 5
+ 5 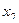 = 0 (l) ( рис. 9 ).
= 0 (l) ( рис. 9 ).
Системе (1) удовлетворяют координаты точек, лежащих на пятиугольнике OABCD и внутри него. Так как прямые (l) и BC не параллельны, то для нахождения оптимального решения системы (1), для которого линейная форма (2) принимает наибольшее значение, достаточно найти значения этой формы в точках A, B, C, D и из полученных чисел выбрать наибольшее. В нашей задаче эти точки имеют следующие координаты: А (20; 0), В (20; 14), С (15, 18), D (0; 18). Подставляя координаты этих точек в (2), получим:
L ( A ) = L (20; 0 ) = 60; L ( B ) = L (20; 14) = 130;
L (C) = L (15; 18) = 135; L (D) = L (0; 18) = 90.
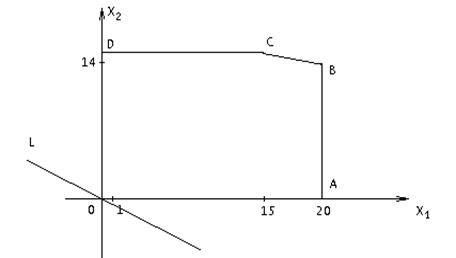
Рис. 9
Следовательно, L = L (15; 18) = 135, то есть предприятию следует приобрести 15 трехтонных и 18 пятитонных автомашин, при их общей грузоподъемностью 135 т.
Вопросы для самопроверки
1. Сформулируйте основную задачу линейного программирования. Приведите примеры.
2. Дайте геометрическую интерпретацию основной задачи линейного программирования.
3. В чем суть симплекс-метода решения задач линейного программирования?
Контрольная работа № 1
В задачах 1 – 20 даны вершины треугольника ABC.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник ABC.
1. А ( -5; 0 ), В ( 7; 9), С ( 5; - 5).
2. А ( -7; 2 ), В ( 5; 11), С ( 3; -3).
3. А ( -5; -3 ), В ( 7; : ), С ( 5; -8).
4. А ( -6; -2 ), В ( 6; 7 ), С ( 4; - 7 ).
5. А ( -8; -4 ), В ( 4; 5 ), С ( 2; - 9 ).
6. А ( 0; -1 ), В ( 12; 8 ), С ( 10; -6 ).
7. А ( -6; 1 ), В ( 6; 10 ), С ( 4; -4 ).
8. А ( -2; -4 ), В ( 10; 5 ), С ( 8; -9 ).
9. А ( -3; 0 ), В ( 9; 9 ), С ( 7; 5 ).
10. А ( -9; -2 ), В ( 3; 7 ), С ( 1; -7 ).
11. А ( -5; 2 ), В ( 7; -7 ), С ( 5; 3 ).
12. А ( -7; 5 ), В ( 5; -4 ), С ( 3; 10 ).
13. А ( -7; 1 ), В ( 5; -8 ), С ( 3; 6 ).
14. А ( 0; 3 ), В ( 12; -6 ), С ( 10; 8 ).
15. А ( -8; 4 ), В ( 4; -5 ), С ( 2; 9 ).
16. А ( -2; 2 ), В ( 10; -7 ), С ( 8; 7 ).
17. А ( 1; 2 ), В ( 13; -7 ), С ( 11; 7 ).
18. А ( -4; 1), В ( 8; -8 ), С ( 6; 6 ).
19. А ( -7; -1 ), В ( -5; -10 ), С ( 3; 4 ).
20. А ( -3; 3 ), В ( 9; -6 ), С ( 7; 8 ).
В задачах 21 – 25 составить уравнение линии, для каждой точки которой отношение расстояний до точки А(x1;y1) и до прямой х=а равно числу ε. Полученное уравнение привести к простейшему виду и построить кривую.
21. А (4; 0 ), а = 9, ε = 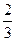 .
.
22. А ( - 8; 0 ), а = - 2, ε = 2
23. А ( 4; 0 ), а = 1, ε = 2 .
24. А ( 9; 0 ), а = 4, ε = 1,5 .
25. А ( -1; 0 ), а = - 4, ε = 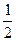 .
.
В задачах 26 – 30 составить уравнение линии, для каждой точки которой ее расстояние до точки А ( 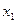 ;
; 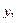 ) равно расстоянию до прямой y=b.
) равно расстоянию до прямой y=b.
Полученное уравнение привести к простейшему виду и построить кривую.
26. А ( 2; 1 ), b = - 1, 27. A ( -2; -2 ), b = - 4.
28. A ( 2; -1 ), b = 2, 29. A ( 2; -1 ), b = 1
30. A ( 4; -1 ), b = 1.
В задачах 31 – 40 даны координаты точек А, В, С. Требуется: 1) записать векторы АВ и АС в системе орт и найти модули этих векторов; 2)
найти угол между векторами 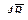 и
и 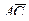 ; 3) составить уравнение плоскости,
; 3) составить уравнение плоскости,
проходящей через точку С перпендикулярно вектору 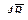 .
.
31. А ( 7; -4; 1 ), В ( 12; -3; 1 ), С ( 10; 1; 5 ).
32. А ( 0; -3; 3 ), В ( 5; -2; 3 ), С ( 3; 2; 7 ).
33. А ( -2; -1; -2 ), В ( 3; 0; -2 ), С ( 1; 4; 2 ).
34. А ( -6; 0; 0 ), В ( -1; 1; 0 ), С ( -3; 5; 4 ).
35. А ( -2; -3; -8 ), В ( 3; -2; -8 ), С ( 1; 2; -4 ).
36. А ( 1; 0; -1 ), В ( 6; 1; -1 ), С ( 4; 5; 3 ).
37. А ( -1; 4; 1 ), В ( 4; 5; 1 ), С ( 2; 9; 5 ).
38. А ( 3; -6; -3 ), В ( 8; -5; -3 ), С ( 6; -1; 1 ).
39. А ( 1; 0; 0 ), В ( 6; 1; 0 ), С ( 4; 5; 4 ).
40. А ( 2; -8; -2 ), В ( 7; -7; -2 ), С ( 5; -3; 2 ).
В задачах 41 – 50 даны векторы 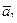 ,
, 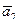 ,
, 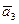 ,
, 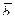 . Показать, что векторы
. Показать, что векторы 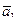 ,
, 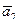 ,
, 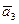 образуют базис трехмерного пространства и найти координаты вектора
образуют базис трехмерного пространства и найти координаты вектора 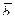 в этом базисе.
в этом базисе.
41. 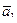 ( 2; 1; 3 ),
( 2; 1; 3 ), 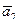 ( 3; -2; 1 ),
( 3; -2; 1 ), 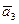 ( 1; -3; - 4 ),
( 1; -3; - 4 ), 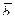 ( 7; 0; 7 ).
( 7; 0; 7 ).
42. 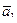 ( 5; 3; 1 ),
( 5; 3; 1 ), 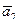 ( -2; -1; 2 ),
( -2; -1; 2 ), 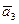 (-2; 1; 4 ),
(-2; 1; 4 ), 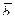 ( 3; 0; 1 ).
( 3; 0; 1 ).
43. 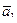 ( 1; 3; 5 ),
( 1; 3; 5 ), 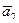 ( -2; -1;-1 ),
( -2; -1;-1 ), 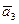 ( 4; -2; 4 ),
( 4; -2; 4 ), 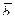 ( -7; 3; -1 ).
( -7; 3; -1 ).
44. 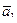 ( 3; 1; 6 ),
( 3; 1; 6 ), 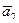 ( -2; 2; -3 ),
( -2; 2; -3 ), 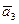 (-4; 5; -1 ),
(-4; 5; -1 ), 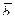 ( 3; 0; 1 ).
( 3; 0; 1 ).
45. 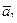 ( 4; 1; 4 ),
( 4; 1; 4 ), 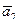 ( -2; -1; 1 ),
( -2; -1; 1 ), 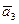 ( 3; 1; 5 ),
( 3; 1; 5 ), 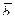 ( -3; -2; 1 ).
( -3; -2; 1 ).
46. 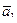 ( 1; 2; 5 ),
( 1; 2; 5 ), 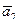 ( 2; -3; 4 ),
( 2; -3; 4 ), 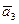 ( 1; -1; -2 ),
( 1; -1; -2 ), 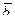 (3; 0; 1 ).
(3; 0; 1 ).
47. 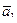 ( 5; 1; 2 ),
( 5; 1; 2 ), 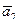 ( 3: 4; -1 ),
( 3: 4; -1 ), 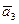 ( -4; 2; 1 ),
( -4; 2; 1 ), 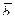 ( -3; 5; 4 ).
( -3; 5; 4 ).
48. 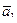 ( 2; 1; 5 ),
( 2; 1; 5 ), 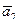 ( -4; 3; 5),
( -4; 3; 5), 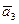 ( 1; -1; -4 ),
( 1; -1; -4 ), 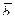 ( 4; -1; -3 ).
( 4; -1; -3 ).
49. 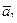 ( 3; 1; 4 ),
( 3; 1; 4 ), 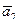 ( - 4; 2; 3 ),
( - 4; 2; 3 ), 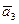 ( 2; -1;-2 ),
( 2; -1;-2 ), 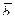 ( 7; -1; 0 ).
( 7; -1; 0 ).
50. 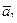 (1; 4; 2 ),
(1; 4; 2 ), 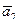 ( 5; -2; -3 ),
( 5; -2; -3 ), 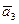 ( - 2; -1; 1 ),
( - 2; -1; 1 ), 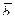 ( -3; 2; 4 ).
( -3; 2; 4 ).
В задачах 51 – 60 систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы .

 x + y – 3z = 0, 2x + 3y + z = 1,
x + y – 3z = 0, 2x + 3y + z = 1,
51. 3x + 2y + 2z = - 1, 52. x + y – 4z = 0,
x – y + 5z = - 2 . 4x + 5y – 3 z = 1.

 3x -2y – z = - 5, x – 4y + 2z = - 5,
3x -2y – z = - 5, x – 4y + 2z = - 5,
53. x + 3y + 2z = 2, 54. 4x + y – 3z = - 3,
5x – 2y + 4z = - 7. 2x + 3y + 4z = 1.

 2x + 4y – 3z = 2, x + 2y – 3z = 1,
2x + 4y – 3z = 2, x + 2y – 3z = 1,
55. x + y + 2z = 0, 56. 2x – 3y – z = - 7,
3x – 2y + z = - 5. 4x + y – 2z = 0.

 3x – y + 4z = 2, 3x – 3y + 2z = -4,
3x – y + 4z = 2, 3x – 3y + 2z = -4,
57. x + 2y + 3z = 7, 58. 2x +y – 3z = - 1,
5x + 3y + 2z = 8. x – 2y + 5z = 1

 4x – y + 3z = 1, 2x – y + 3z = 1,
4x – y + 3z = 1, 2x – y + 3z = 1,
59. 3x + 2y + 4z = 8, 60. x -2y – 5z = - 9
2x – 2y + 4z = 0. 4x + 3y – 2z = 4.
В задачах 61 – 80 найти указанные пределы .
61. а) 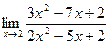 ; б)
; б) 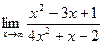 ;
;
в) 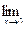
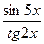 ; г)
; г) 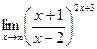
62. a) 
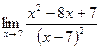 ; б)
; б) 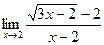 ;
;
в) 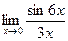 ; г)
; г) 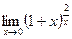 ;
;
63. a) 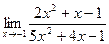 ; б)
; б) 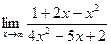 ;
;
в) 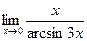 ; г)
; г) 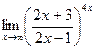 ;
;
64. a) 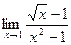 ; б)
; б) 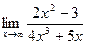 ;
;
в) 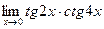 ; г)
; г) 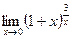 ;
;
65. a) 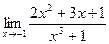 ; б)
; б) 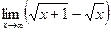 ;
;
в) 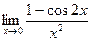 ; г)
; г) 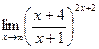 ;
;
66. a) 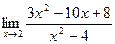 ; б)
; б) 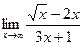 ;
;
в) 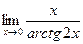 ; г)
; г) 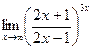 .
.
67. a) 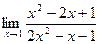 ; б)
; б) 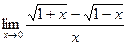 ;
;
в) 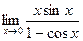 ; г)
; г) 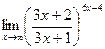 ;
;
68. a) 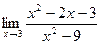 ; б)
; б) 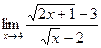 ;
;
в) 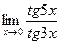 ; г)
; г) 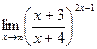 .
.
69. a) 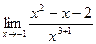 ; б)
; б) 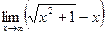 ;
;
в) 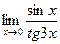 ; г)
; г) 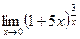 ;
;
70. a) 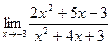 ; б)
; б) 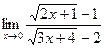 ;
;
в) 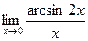 ; г)
; г) 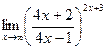 .
.
71. a) 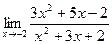 ; б)
; б) 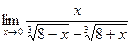 ;
;
в) 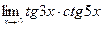 ; г)
; г) 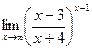 .
.
72. a) 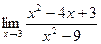 ; б)
; б) 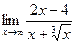 ;
;
в) 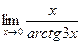 ; г)
; г) 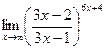 .
.
73. a) 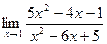 ; б)
; б) 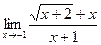 ;
;
в) 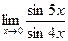 ; г)
; г) 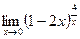 .
.
74. a) 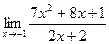 ; б)
; б) 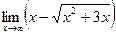 ;
;
в) 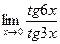 ; г)
; г) 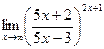 .
.
75. a) 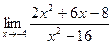 ; б)
; б) 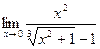 ;
;
в) 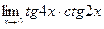 ; г)
; г) 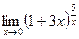 .
.
76. a) 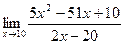 ; б)
; б) 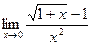 ;
;
в) 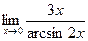 ; г)
; г)  .
.
77. a)  ; б)
; б) 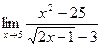 ;
;
в) 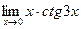 ; г)
; г) 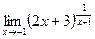 .
.
78. a) 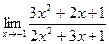 ; б)
; б) 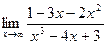 ;
;
в) 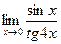 ; г)
; г) 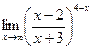 .
.
79. a) 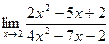 ; б)
; б) 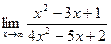 ;
;
в) 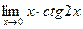 ; г)
; г) 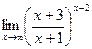 .
.
80. a) 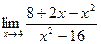 ; б)
; б) 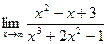 ;
;
в) 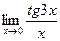 ; г)
; г) 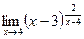 .
.
Контрольная работа № 2
В задачах 81 – 100 найти производные функций
81. а) 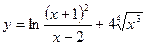 ; б)
; б) 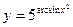
в) 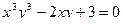 .
.
82. a) 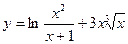 ; б)
; б) 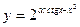 ;
;
в) 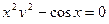 .
.
83. a) 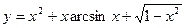 ; б)
; б) 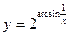 ;
;
в) 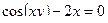 .
.
84. a) 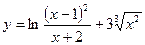 ; б)
; б) 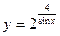 ;
;
в) 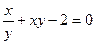 .
.
85. a) 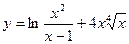 ; б)
; б) 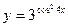 ;
;
в) 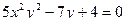 .
.
86. a) 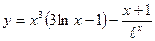 ; б)
; б) 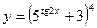 ;
;
в) 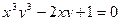 .
.
87. a) 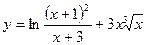 ; б)
; б) 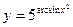 ;
;
в) 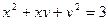 .
.
88. a) 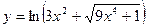 ; б)
; б) 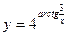 ;
;
в) 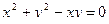 .
.
89. a) 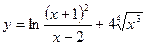 ; б)
; б) 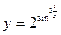 ;
;
в) 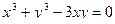 .
.
90. a) 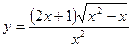 ; б)
; б) 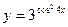 ;
;
в) 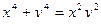 .
.
91. a) 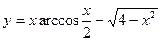 ; б)
; б) 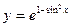 ;
;
в) 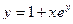 .
.
92. a) 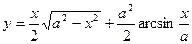 ; б)
; б) 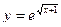 ;
;
в) 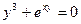 .
.
93. a) 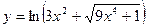 ; б)
; б) 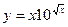 ;
;
в) 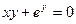 .
.
94. a) 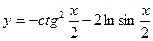 ; б)
; б) 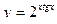
в) 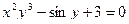 .
.
95. a) 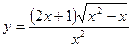 ; б)
; б) 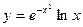 ;
;
в) 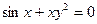 .
.
96. a) 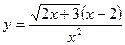 ; б)
; б) 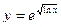 ;
;
в) 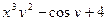 .
.
97. a) 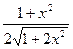 ; б)
; б) 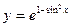 ;
;
в) 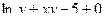 .
.
98. a) 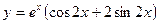 ; б)
; б) 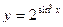 ;
;
в) 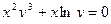 .
.
99. a) 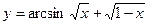 ; б)
; б) 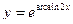
 ;
;
в) 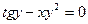 .
.
100. a) 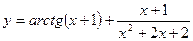 ; б)
; б) 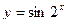 ;
;
в) 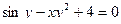 .
.
В задачах 101 - 102 исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции .
101. 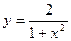 . 102.
. 102. 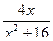 . 103.
. 103. 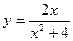 .
.
104. 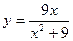 . 105.
. 105. 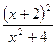 . 106.
. 106. 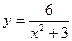 .
.
107. 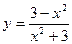 . 108.
. 108. 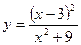 . 109.
. 109. 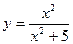 .
.
110. 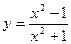 . 111.
. 111. 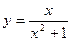 . 112.
. 112. 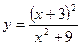 .
.
113. 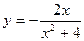 . 114.
. 114. 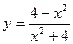 . 115.
. 115. 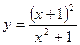 .
.
116. 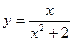 . 117.
. 117. 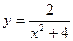 . 118.
. 118. 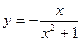 .
.
119. 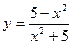 . 120.
. 120. 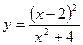 .
.
121. Каковы радиус основания R и высота H открытого цилиндрического бака данного объема V, чтобы на его изготовление пошло наименьшее количество листового металла?
122. Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения 18 м. При каком радиусе полукруга площадь сечения будет наибольшей?
123. Найти стороны прямоугольника наибольшей площади, которой можно вписать в эллипс 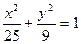 .
.
124. Найти наибольший объем цилиндра, полная поверхность которого равна S.
125. Найти наибольший объем конуса, образующая которого равна l.
126. Определить размеры открытого бассейна с квадратным дном объемом 32 м³ так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
127. Сумма двух положительных чисел равна а . Каковы эти числа, если сумма их кубов будет наименьшей?
128. Два коридора шириной 2,4 м и 1,6 м пересекаются под прямым углом. Определить наибольшую длину лестницы, которую можно перенести горизонтально из одного коридора в другой.
129. На параболе y = x² найти точку, наименее удаленную от прямой y = 2x – 4.
130. Из всех прямоугольников, вписанных в круг радиуса R, найти тот, который имеет наибольшую площадь.
В задачах 131 – 135 исследовать на экстремум функцию z = f ( x, y ).
131. z = 3x + 3y - x² - xy - y² + 6.
132. z = 7x + 8y - x² - xy – y² - 10.
133. z = 8x – 4y + x² - xy + y² +15.
134. z = x² + y² - 6x – 8y + 12.
135. z = 2x – 8y - x² - y² - 9.
В задачах 136 -140 найти наименьшее и наибольшее значения функции z = f ( x, y ) в данной замкнутой область.
136. z = x² + xy – 6x – 2y + 2 в прямоугольнике 1 ≤ x ≤ 3, 1 ≤ y ≤ 4.
137. z = x² + 4xy - y² - 5 в треугольнике, ограниченном осями Ox и Oy и прямой y = 2 – x.
138. z = x² + y² - 10x – 2y + 15 в прямоугольнике 2 ≤ x ≤ 6,0 ≤ y ≤ 5.
139. z = x² - 2xy + 4x – 4y + 7 в области, ограниченной параболой y = - x² - 4x и осью Ox.
140. z = x² + 2y² + 4xy + 2x + 4y + 2 в квадрате 0 ≤ x ≤ 2, 0 ≤ x ≤ 2.
В задачах 141 – 160 найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.
141. a) 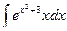 ; б)
; б) 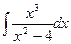 ;
;
в) 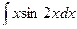 .
.
142. a) 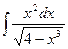 ; б)
; б) 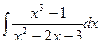 ;
;
в) 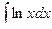 .
.
143. a) 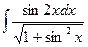 ; б)
; б) 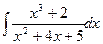 ;
;
в)  .
.
144. a) 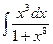 ; б)
; б) 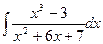 ;
;
в) 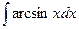 .
.
145. a) 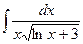 ; б)
; б) 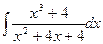 ;
;
в) 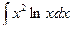 .
.
146. a) 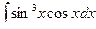 ; б)
; б) 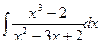 ;
;
в) 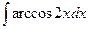 .
.
147. a) 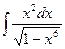 ; б)
; б) 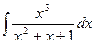 ;
;
в) 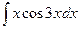 .
.
148. a) 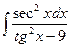 ; б)
; б) 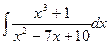 ;
;
в) 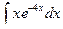 .
.
149. a) 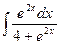 ; б)
; б) 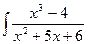 ;
;
в) 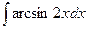 .
.
150. a) 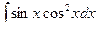 ; б)
; б) 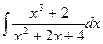 ;
;
в) 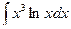 .
.
151. a) 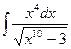 ; б)
; б) 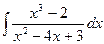 ;
;
в) 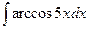 .
.
152. a) 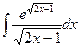 ; б)
; б) 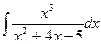 ;
;
в) 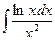 .
.
153. a) 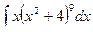 ; б)
; б) 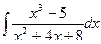 ;
;
в) 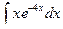 .
.
154. a) 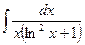 ; б)
; б) 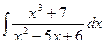 ;
;
в) 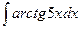 .
.
155. a) 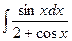 ; б)
; б) 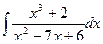 ;
;
в) 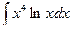 .
.
156 a) 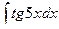 ; б)
; б) 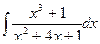 ;
;
в) 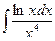 .
.
157. a) 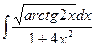 ; б)
; б) 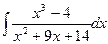 ;
;
в) 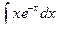 .
.
158. a) 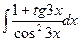 ; б)
; б) 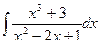 ;
;
в) 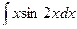 .
.
159. a) 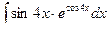 ; б)
; б) 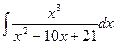 ;
;
в) 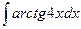 .
.
160. a) 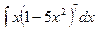 ; б)
; б) 
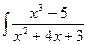 ;
;
в) 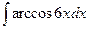 .
.
В задачах 161-170 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
161. y=x³; 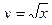 .
.
162. 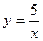 ; y=6-x.
; y=6-x.
163. 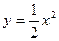 ; y=4-x.
; y=4-x.
164. y=x² +2; y=4-x².
165. y=-x²+1; y=x-1
166. y=x² - 4x +4; y=x.
167. 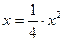 ; y²=4x.
; y²=4x.
168. 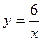 ; y=7-x.
; y=7-x.
169. y=3x²+1;y=3x+7.
170. y=2x-x²; y=-x.
В задачах 171 – 175 вычислить объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной указанными линиями. Сделать чертеж.
171. y ² = x; y = x ².
172. xy = 4; x = 1; x = 4; y = 0 .
173. y = sin x ( одна полуволна ); y = 0 .
174. y = x ² + 1; y = 3x – 1.
175. 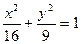
В задачах 176 – 180 вычислить объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной указанными линиями. Сделать чертеж.
176. y ² = 4 – x; x = 0.
177. 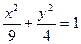 .
.
178. x + y – 2 = 0; x = 0; y = 0.
179. xy = 2; x = 0; y = 4.
180. y = - x ² + 4; x = 0; y = 0; y = 3.
Контрольная работа № 3
В задачах 181 – 200 найти общее решение дифференциальных уравнений первого порядка .
181. 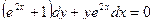 . 182.
. 182. 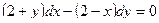 .
.
183. 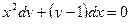 . 184.
. 184. 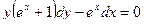 .
.
185. 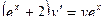 . 186.
. 186. 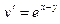 .
.
187. 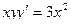 . 188.
. 188. 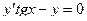 .
.
189. 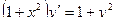 . 190
. 190 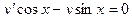 .
.
191. 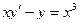 . 192.
. 192. 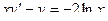 .
.
193. 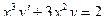 . 194.
. 194. 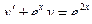 .
.
195. 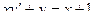 . 196.
. 196. 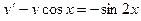 .
.
197.  . 198.
. 198. 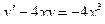 .
.
199. 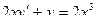 . 200.
. 200. 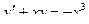 .
.
В задачах 201 – 210 найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям .
201. 
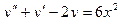 ,
, 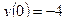 ,
, 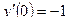 .
.
202. 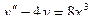 ,
, 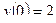 ,
, 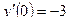 .
.
203. 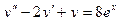 ,
, 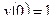 ,
, 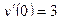 .
.
204. 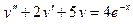 ,
, 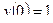 ,
, 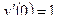 .
.
205. 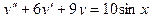 ,
, 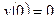 ,
, 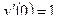 .
.
206. 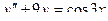 ,
, 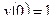 ,
, 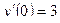 .
.
207. 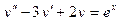 ,
, 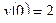 ,
, 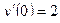 .
.
208. 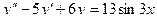 ,
, 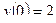 ,
, 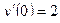 .
.
209. 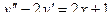 ,
, 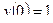 ,
, 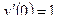 .
.
210. 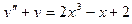 ,
, 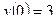 ,
, 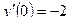 .
.
В задачах 211 -230 дан степенной ряд 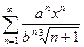 .
.
При заданных значениях a и b написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
211. а = 2, b = 3. 212. a = 3, b = 5.
213. a = 4, b = 7 . 214. a = 5, b = 9.
215. a = 7, b = 6 . 216 a = 2, b = 5.
217. a = 3, b = 2. 218. a = 4, b = 3.
219. a = 5, b = 2. 220. a = 6, b = 4.
221. a = 3, b = 7. 222. a = 4, b = 5.
223. a = 8, b = 3. 224. a = 7, b = 4.
225. a = 5, b = 7. 226. a = 2, b = 6.
227. a = 3, b = 4. 228. a = 7, b = 5.
229. a = 5, b = 8. 230. a = 2, b = 4.
В задачах 231 – 250 вычислить определенный интеграл с точностью до 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
231. 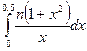 . 232.
. 232. 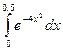 .
.
233. 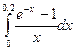 . 234.
. 234. 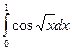 .
.
235. 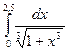 . 236.
. 236. 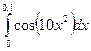 .
.
237. 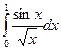 . 238.
. 238. 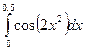 .
.
239. 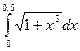 . 240.
. 240. 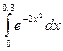 .
.
241 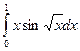 . 242.
. 242. 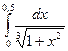 .
.
243. 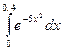 . 244.
. 244. 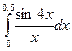 .
.
245. 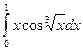 . 246.
. 246. 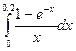 .
.
247. 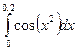 . 248.
. 248. 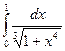 .
.
249. 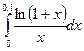 . 250.
. 250. 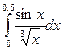 .
.
Контрольная работа № 4
251. В читальном зале имеется 6 учебников по теории вероятности, из которых 2 в мягком переплете. Библиотекарь взял два учебника. Найти вероятность того, что оба учебника окажутся в мягком переплете.
252. Студент знает ответы на 20 из25 вопросов программы. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором три вопроса.
253. Для некоторой местности в июле шесть пасмурных дней. Найти вероятность того, что первого и второго июля будет ясная погода.
254. Из 200 рабочих норму выработки не выполняют 15 человек. Найти вероятность того, что два случайно выбранных рабочих не выполняют норму.
255. Три стрелка по мишени. Вероятность попадания в цель первым стрелком равна 0,6, вторым – 0,7, третьим – 0,8. Найти вероятность того, что при одном выстреле попадут в цель : а) все три стрелка; б) попадет хотя бы один из них.
256. В ящике лежат 20 электрических лампочек, из которых 2 нестандартные . Найти вероятность того, что взятые одна за другой две лампочки окажутся стандартными.
257. Одновременно бросаются две игральные кости. Найти вероятность того, что на каждой кости появится нечетное количество очков.
258. Из заготовленной для посева пшеницы зерно первого сорта составляет 40 %, второго сорта – 50 %, третьего сорта – 10 %. Вероятность того, что взойдет зерно первого сорта равна 0,8, второго – 0,5, третьего – 0,3. Найти вероятность того, что взойдут наугад взятое зерно.
259. В магазин поступили телевизоры из трех заводов. Вероятность того, что телевизор изготовлен на первом заводе, равна 0,3, на втором – 0,2, на третьем - 0,5. Вероятность того, что телевизор окажется бракованным, для первого завода равна 0,2, для второго – 0,1, для третьего – 0,3. Найти вероятность того, что наугад взятый телевизор окажется небракованным.
260. В мастерской на трех станках изготавливаются однотипные детали. Вероятность безотказной работы первого станка равна 0,8, второго – 0,7, третьего – 0,9. Вероятность изготовления бракованной детали на первом станке равна 0,2, на втором – 0,3, на третьем – 0,1. Найти вероятность того, что наугад выбранная деталь окажется стандартной.
261. Вероятность попадания в цель при одном выстреле равна 0,7. Производится 4 выстрела. Найти вероятность того, что цель будет поражена: а) три раза; б) не более двух раз.
262. Вероятность всхожести пшеницы равна 0,8. Какова вероятность того, что из 5 семян взойдут не менее 3?
263. Вероятность попадания в цель при одном выстреле равна 0,8. Написать закон распределения вероятностей попаданий в цель при 5 выстрелах и построить многоугольник распределения вероятностей.
264. Всхожесть семян пшеницы составляет 90 %. Определить наиболее вероятное число всходов из 200 посеянных семян.
265. Семена пшеницы содержат 0,2% сорняков. Найти вероятность того, что в 1000 семян будет 6 семян сорняков.
В задачах 266 – 270 дана вероятность p того, что семя злака прорастет. Найти вероятность того, что из n посеянных семян прорастет ровно R семян.
266. n = 100, p = 0,9, R = 95.
267. n = 400, p = 0,8, R = 330.
268. n = 900, p = 0,36, R = 340.
269. n = 225, p = 0,64, R = 158.
270. n = 250, p = 0,81, R = 200.
В задачах 271-280 дана вероятность р появления события А в каждом из n независимых испытаний. Найти вероятность того, что в этих испытаниях событие А появится не менее 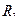 раз и не более
раз и не более 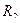 раз.
раз.
271. n=360, p=0,8, 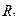 =280,
=280, 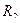 =300.
=300.
272. n=490, p=0,6, 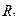 =320,
=320, 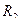 =350.
=350.
273. n=640, p=0,9, 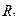 =500,
=500, 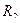 =540.
=540.
274. n=225, p=0,2, 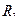 =50,
=50, 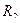 =60.
=60.
275. n=810, p=0,4, 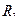 =340,
=340, 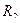 =400.
=400.
276. n=250, p=0,7, 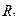 =150,
=150, 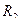 =180.
=180.
277. n=300, p=0,3, 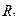 =110,
=110, 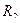 =130.
=130.
278. n=625, p=0,8, 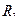 =480,
=480, 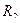 =500.
=500.
279. n=100, p=0,5, 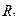 =60,
=60, 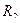 =80.
=80.
280. n=256, p=0,9, 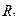 =200,
=200, 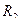 =220.
=220.
В задачах 281 – 290 задан закон распределения дискретной случайной величины Х ( в первой строке указаны возможные значения величины Х, во второй строке даны вероятности p этих значений ). Найти: 1) математическое ожидание M (X); 2) дисперсию D (X); 3) среднее квадратическое отклонение σ.
281. X 8 4 6 5
p 0,1 0,3 0,2 0,4
282. X 23 25 27 29
p 0,2 0,1 0,3 0,4
283. X 10 8 6 9
p 0,4 0,1 0,3 0,2
284. X 32 40 37 35
p 0,1 0,3 0,4 0,2
285. X 42 41 43 45
p 0,3 0,3 0,2 0,2
286. X 15 11 13 12
p 0,2 0,5 0,2 0,1
287. X 52 54 57 51
p 0,1 0,4 0,3 0,2
288. X 21 20 22 26
p 0,5 0,2 0,2 0,1
289. X 34 30 32 36
p 0,2 0,4 0,3 0,1
290. X 50 48 51 53
p 0,3 0,2 0,2 0,3
В задачах 291 – 300 случайная величина Х задана интегральной функцией распределения F ( x ). Найти: 1) дифференциальную функцию распределения f (x); 2) математическое ожидание M ( X ); 3) дисперсию D ( X ).
 291. 0 при х < 0,
291. 0 при х < 0,
F (x) = x ² при 0 ≤ х ≤ 1,
1 при х > 1.
 292. 0 при х<0,
292. 0 при х<0,
F (x) = 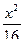 при 0≤х≤4,
при 0≤х≤4,
1 при х>4.
 293. 0 при х<2,
293. 0 при х<2,
F (x) = х-2 при 2 ≤ х ≤ 3,
1 при х>3.
 294. 0 при х<0,
294. 0 при х<0,
F (x) = 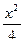 при 0 ≤ х ≤ 2,
при 0 ≤ х ≤ 2,
1 при х>2.

295. 0 при х>4,
F (x) = х – 4 при 4 ≤ х ≤ 5,
1 при х>5.

296. 0 при х<0,
F (x) = 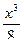 при 0 ≤ х ≤ 2,
при 0 ≤ х ≤ 2,
1 при х > 2.
 297. 0 при х < 0,
297. 0 при х < 0,
F (x) = 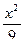 при 0 ≤ х ≤ 3,
при 0 ≤ х ≤ 3,
1 при х > 3.
 299. 0 при х < 0,
299. 0 при х < 0,
F (x) = х при 0 ≤ х ≤ 1,
1 при х > 1.
 300. 0 при х < 0,
300. 0 при х < 0,
F (x) = 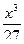 при 0 ≤ х ≤ 3,
при 0 ≤ х ≤ 3,
1 при х > 3.
301. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм . Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Найти процент стандартных деталей.
302. Средний диаметр стволов деревьев на некотором участке равен 25 см, среднее квадратическое отклонение равно 5 см. считая диаметр ствола случайной величины, распределенной нормально, найти процент деревьев, имеющих диаметр свыше 20 см.
303. Процент всхожести семян равен 90%. Оценить вероятность того, что из 1000 посеянных семян взойдут от 850 до 950 семян включительно.
304. Среднее квадратическое отклонение нормально распределенной случайной величины равно 0,5. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не превосходит 1.
305. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 150 мм и средним квадратическим отклонением 0,5 мм. Какую точность размера детали можно гарантировать с вероятностью 0,95.
306. Средний вес зерна равен 0,2 г, среднее квадратическое отклонение равно 0,05 г. Определить вероятность того, что вес наудачу взятого зерна окажется в пределах от 0,16 г до 0,22 г.
307. норма высева семян на 1 га равна 200 кг. Фактический расход семян на 1 га колеблется около этого значения со средним квадратическим 10 кг. Определить количество семян, обеспечивающих посев на площадь 100 га с гарантией 0,95.
308. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм. Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилось и характеризуется средним квадратическим отклонением 0,4 мм. На сколько повысился процент бракованных деталей?
309. Масса яблок, средняя величина которой равна 150 г, является нормально распределенной случайной величиной со средним квадратическим отклонением 20 г. Найти вероятность того, что масса наугад взятого яблока будет заключена в пределах от 130 г до 180 г.
310. Устройство состоит из 20 однотипных независимо работающих элементов. Вероятность безотказной работы каждого элемента за 10 часов 0,9. Оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом отказов за 10 часов окажется меньше двух.
Задачи 311 – 320. Хозяйство имеет возможность приобрести не более 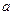 трехтонных автомашин и не более
трехтонных автомашин и не более 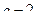 пятитонных автомашин. Отпускная цена трехтонного грузовика – 4 000 у.е., а пятитонного – 5 000 у.е. Хозяйство может выделить для приобретения автомашин
пятитонных автомашин. Отпускная цена трехтонного грузовика – 4 000 у.е., а пятитонного – 5 000 у.е. Хозяйство может выделить для приобретения автомашин 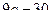 тыс. у.е. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной? Задачу решить графическим методом. Значения параметра
тыс. у.е. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной? Задачу решить графическим методом. Значения параметра 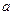 даны в таблице:
даны в таблице:
| Номер задания | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 |
Значение 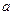
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Приложение 1
ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ 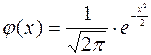
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 0,3989 | 3989 | 3989 | 3988 | 3986 | 3984 | 3982 | 3980 | 3977 | 3973 |
| 0,1 | 3970 | 3965 | 3961 | 3956 | 3951 | 3945 | 3939 | 3932 | 3925 | 3918 |
| 0,2 | 3910 | 3902 | 3894 | 3885 | 3876 | 3867 | 3857 | 3847 | 3836 | 3825 |
| 0,3 | 3814 | 3802 | 3790 | 3778 | 3765 | 3752 | 3739 | 3726 | 3712 | 3697 |
| 0,4 | 3683 | 3668 | 3653 | 3637 | 3621 | 3605 | 3589 | 3572 | 3555 | 3538 |
| 0,5 | 3521 | 3508 | 3485 | 3467 | 3448 | 3429 | 3410 | 3391 | 3372 | 3352 |
| 0,6 | 3332 | 3312 | 3292 | 3271 | 3251 | 3230 | 3209 | 3187 | 3166 | 3144 |
| 0,7 | 3123 | 3101 | 3079 | 3056 | 3034 | 3011 | 2989 | 2966 | 2943 | 2920 |
| 0,8 | 2897 | 2874 | 2850 | 2827 | 2803 | 2780 | 2756 | 2732 | 2709 | 2685 |
| 0,9 | 2661 | 2637 | 2613 | 2589 | 2565 | 2541 | 2516 | 2492 | 2468 | 2444 |
| 1,0 | 0,2420 | 2396 | 2371 | 2347 | 2323 | 2299 | 2275 | 2251 | 2227 | 2203 |
| 1,1 | 2179 | 2155 | 2131 | 2107 | 2083 | 2059 | 2036 | 2012 | 1989 | 1965 |
| 1,2 | 1942 | 1919 | 1895 | 1872 | 1849 | 1826 | 1804 | 1781 | 1758 | 1736 |
| 1,3 | 1714 | 1691 | 1669 | 1647 | 1626 | 1604 | 1582 | 1561 | 1539 | 1518 |
| 1,4 | 1497 | 1476 | 1456 | 1435 | 1415 | 1394 | 1374 | 1354 | 1334 | 1315 |
| 1,5 | 1295 | 1276 | 1257 | 1238 | 1219 | 1200 | 1182 | 1163 | 1145 | 1127 |
| 1,6 | 1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 1006 | 0989 | 0973 | 0957 |
| 1,7 | 0940 | 0925 | 0909 | 0893 | 0878 | 0863 | 0848 | 0833 | 0818 | 0804 |
| 1,8 | 0790 | 0775 | 0761 | 0748 | 0734 | 0721 | 0707 | 0694 | 0681 | 0669 |
| 1,9 | 0656 | 0644 | 0632 | 0620 | 0608 | 0598 | 0584 | 0573 | 0562 | 0551 |
| 2,0 | 0,0640 | 0529 | 0519 | 0508 | 0498 | 0488 | 0478 | 0468 | 0459 | 0449 |
| 2,1 | 0440 | 0431 | 0422 | 0413 | 0404 | 0396 | 0387 | 0379 | 0371 | 0363 |
| 2,2 | 0355 | 0347 | 0339 | 0332 | 0326 | 0317 | 0310 | 0303 | 0297 | 0290 |
| 2,3 | 0283 | 0277 | 0270 | 0264 | 0258 | 0252 | 0246 | 0241 | 0235 | 0229 |
| 2,4 | 0224 | 0219 | 0213 | 0208 | 0203 | 0198 | 0194 | 0189 | 0184 | 0180 |
| 2,5 | 0175 | 0171 | 0167 | 0163 | 0158 | 0154 | 0151 | 0147 | 0143 | 0139 |
| 2,6 | 0136 | 0132 | 0129 | 0126 | 0122 | 0119 | 0116 | 0113 | 0110 | 0107 |
| 2,7 | 0104 | 0101 | 0099 | 0096 | 0093 | 0091 | 0088 | 0086 | 0084 | 0081 |
| 2,8 | 0079 | 0077 | 0075 | 0073 | 0071 | 0069 | 0067 | 0065 | 0063 | 0061 |
| 2,9 | 0060 | 0058 | 0056 | 0055 | 0053 | 0051 | 0050 | 0048 | 0047 | 0046 |
| 3,0 | 0,0044 | 0043 | 0042 | 0040 | 0039 | 0038 | 0037 | 0036 | 0035 | 0034 |
| 3,1 | 0033 | 0032 | 0031 | 0030 | 0029 | 0028 | 0027 | 0026 | 0025 | 0025 |
| 3,2 | 0024 | 0023 | 0022 | 0022 | 0021 | 0020 | 0020 | 0019 | 0018 | 0018 |
| 3,3 | 0017 | 0017 | 0016 | 0016 | 0015 | 0015 | 0014 | 0014 | 0013 | 0013 |
| 3,4 | 0012 | 0012 | 0012 | 0011 | 0011 | 0011 | 0010 | 0010 | 0009 | 0009 |
| 3,5 | 0009 | 0008 | 0008 | 0008 | 0008 | 0007 | 0007 | 0007 | 0007 | 0006 |
| 3,6 | 0006 | 0006 | 0005 | 0005 | 0005 | 0005 | 0005 | 0005 | 0005 | 0004 |
| 3,7 | 0004 | 0004 | 0004 | 0004 | 0004 | 0004 | 0003 | 0003 | 0003 | 0003 |
| 3,8 | 0003 | 0003 | 0003 | 0003 | 0003 | 0002 | 0002 | 0002 | 0002 | 0002 |
| 3,9 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0001 | 0001 |
Приложение 2
ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ 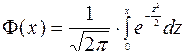
| х | Ф(х) | х | Ф(х) | х | Ф(х) | х | Ф(х) |
| 0,00 | 0,0000 | 0,30 | 0,1179 | 0,60 | 0,2257 | 0,90 | 0,3159 |
| 0,01 | 0,0040 | 0,31 | 0,1217 | 0,61 | 0,2291 | 0,91 | 0,3186 |
| 0,02 | 0,0080 | 0,32 | 0,1255 | 0,62 | 0,2324 | 0,92 | 0,3212 |
| 0,03 | 0,0120 | 0,33 | 0,1293 | 0,63 | 0,2357 | 0,93 | 0,3238 |
| 0,04 | 0,0160 | 0,34 | 0,1331 | 0,64 | 0,2389 | 0,94 | 0,3264 |
| 0,05 | 0,0199 | 0,35 | 0,1368 | 0,65 | 0,2422 | 0,95 | 0,3289 |
| 0,06 | 0,0239 | 0,36 | 0,1406 | 0,66 | 0,2454 | 0,96 | 0,3315 |
| 0,07 | 0,0279 | 0,37 | 0,1443 | 0,67 | 0,2486 | 0,97 | 0,3340 |
| 0,08 | 0,0319 | 0,38 | 0,1480 | 0,68 | 0,2517 | 0,98 | 0,3365 |
| 0,09 | 0,0359 | 0,39 | 0,1517 | 0,69 | 0,2549 | 0,99 | 0,3389 |
| 0,10 | 0,0398 | 0,40 | 0,1554 | 0,70 | 0,2580 | 1,00 | 0,3413 |
| 0,11 | 0,0438 | 0,41 | 0,1591 | 0,71 | 0,2611 | 1,01 | 0,3438 |
| 0,12 | 0,0478 | 0,42 | 0,1628 | 0,72 | 0,2642 | 1,02 | 0,3461 |
| 0,13 | 0,0517 | 0,43 | 0,1664 | 0,73 | 0,2673 | 1,03 | 0,3485 |
| 0,14 | 0,0557 | 0,44 | 0,1700 | 0,74 | 0,2703 | 1,04 | 0,3508 |
| 0,15 | 0,0596 | 0,45 | 0,1736 | 0,75 | 0,2734 | 1,05 | 0,3531 |
| 0,16 | 0,0636 | 0,46 | 0,1772 | 0,76 | 0,2764 | 1,06 | 0,3554 |
| 0,17 | 0,0675 | 0,47 | 0,1808 | 0,77 | 0,2794 | 1,07 | 0,3557 |
| 0,18 | 0,0714 | 0,48 | 0,1844 | 0,78 | 0,2823 | 1,08 | 0,3599 |
| 0,19 | 0,0753 | 0,49 | 0,1879 | 0,79 | 0,2852 | 1,09 | 0,3621 |
| 0,20 | 0,0793 | 0,50 | 0,1915 | 0,80 | 0,2881 | 1,10 | 0,3643 |
| 0,21 | 0,0832 | 0,51 | 0,1950 | 0,81 | 0,2910 | 1,11 | 0,3665 |
| 0,22 | 0,0871 | 0,52 | 0,1985 | 0,82 | 0,2939 | 1,12 | 0,3686 |
| 0,23 | 0,0910 | 0,53 | 0,2019 | 0,83 | 0,2967 | 1,13 | 0,3708 |
| 0,24 | 0,0948 | 0,54 | 0,2054 | 0,84 | 0,2995 | 1,14 | 0,3729 |
| 0,25 | 0,0987 | 0,55 | 0,2088 | 0,85 | 0,3023 | 1,15 | 0,3749 |
| 0,26 | 0,1026 | 0,56 | 0,2123 | 0,86 | 0,3051 | 1,16 | 0,3770 |
| 0,27 | 0,1064 | 0,57 | 0,2157 | 0,87 | 0,3078 | 1,17 | 0,3790 |
| 0,28 | 0,1103 | 0,58 | 0,2190 | 0,88 | 0,3106 | 1,18 | 0,3810 |
| 0,29 | 0,1141 | 0,59 | 0,2224 | 0,89 | 0,3133 | 1,19 | 0,3830 |
| 1,20 | 0,3849 | 1,56 | 0,4406 | 1,92 | 0,4726 | 2,56 | 0,4948 |
| 1,21 | 0,3869 | 1,57 | 0,4418 | 1,93 | 0,4732 | 2,58 | 0,4951 |
| 1,22 | 0,3883 | 1,58 | 0,4429 | 1,94 | 0,4738 | 2,60 | 0,4953 |
| 1,23 | 0,3907 | 1,59 | 0,4441 | 1,95 | 0,4744 | 2,62 | 0,4956 |
| 1,24 | 0,3925 | 1,60 | 0,4452 | 1,96 | 0,4750 | 2,64 | 0,4959 |
| 1,25 | 0,3944 | 1,61 | 0,4463 | 1,97 | 0,4756 | 2,66 | 0,4961 |
| 1,26 | 0,3962 | 1,62 | 0,4474 | 1,98 | 0,4761 | 2,68 | 0,4963 |
| 1,27 | 0,3980 | 1,63 | 0,4484 | 1,99 | 0,4767 | 2,70 | 0,4965 |
| 1,28 | 0,3997 | 1,64 | 0,4495 | 2,00 | 0,4772 | 2,72 | 0,4967 |
| 1,29 | 0,4015 | 1,65 | 0,4505 | 2,02 | 0,4783 | 2,74 | 0,4969 |
| 1,30 | 0,4032 | 1,66 | 0,4515 | 2,04 | 0,4793 | 2,76 | 0,4971 |
| 1,31 | 0,4049 | 1,67 | 0,4525 | 2,06 | 0,4803 | 2,78 | 0,4973 |
| 1,32 | 0,4066 | 1,68 | 0,4535 | 2,08 | 0,4812 | 2,80 | 0,4974 |
| 1,33 | 0,4082 | 1,69 | 0,4545 | 2,10 | 0,4821 | 2,82 | 0,4976 |
| 1,34 | 0,4099 | 1,70 | 0,4554 | 2,12 | 0,4830 | 2,84 | 0,4977 |
| 1,35 | 0,4115 | 1,71 | 0,4564 | 2,14 | 0,4838 | 2,86 | 0,4979 |
| 1,36 | 0,4131 | 1,72 | 0,4573 | 2,16 | 0,4846 | 2,88 | 0,4980 |
| 1,37 | 0,4147 | 1,73 | 0,4582 | 2,18 | 0,4854 | 2,90 | 0,4981 |
| 1,38 | 0,4162 | 1,74 | 0,4591 | 2,20 | 0,4861 | 2,92 | 0,4982 |
| 1,39 | 0,4177 | 1,75 | 0,4599 | 2,22 | 0,4868 | 2,94 | 0,4984 |
| 1,40 | 0,4192 | 1,76 | 0,4608 | 2,24 | 0,4875 | 2,96 | 0,4985 |
| 1,41 | 0,4207 | 1,77 | 0,4616 | 2,26 | 0,4881 | 2,98 | 0,4986 |
| 1,42 | 0,4222 | 1,78 | 0,4625 | 2,28 | 0,4887 | 3,00 | 0,49865 |
| 1,43 | 0,4236 | 1,79 | 0,4633 | 2,30 | 0,4893 | 3,20 | 0,49931 |
| 1,44 | 0,4251 | 1,80 | 0,4641 | 2,32 | 0,4898 | 3,40 | 0,49966 |
| 1,45 | 0,4265 | 1,81 | 0,4649 | 2,34 | 0,4904 | 3,60 | 0,499841 |
| 1,46 | 0,4279 | 1,82 | 0,4656 | 2,36 | 0,4909 | 3,80 | 0,499928 |
| 1,47 | 0,4292 | 1,83 | 0,4664 | 2,38 | 0,4913 | 4,00 | 0,499968 |
| 1,48 | 0,4306 | 1,84 | 0,4671 | 2,40 | 0,4918 | 4,50 | 0,499997 |
| 1,49 | 0,4319 | 1,85 | 0,4678 | 2,42 | 0,4922 | 5,00 | 0,499997 |
| 1,50 | 0,4332 | 1,86 | 0,4686 | 2,44 | 0,4927 | ||
| 1,51 | 0,4345 | 1,87 | 0,4693 | 2,46 | 0,4931 | ||
| 1,52 | 0,4357 | 1,88 | 0,4699 | 2,48 | 0,4934 | ||
| 1,53 | 0,4370 | 1,89 | 0,4706 | 2,50 | 0,4938 | ||
| 1,54 | 0,4382 | 1,90 | 0,4713 | 2,52 | 0,4941 | ||
| 1,55 | 0,4394 | 1,91 | 0,4719 | 2,54 | 0,4945 |
ОГЛАВЛЕНИЕ
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3
Содержание программы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6
Указания к выполнению контрольной работы №1 . . . . . . . . . . . . . . . . 11
Указания к выполнению контрольной работы №2 . . . . . . . . . . . . . . . . 23
Указания к выполнению контрольной работы №3 . . . . . . . . . . . . . . . . 31
Указания к выполнению контрольной работы №4 . . . . . . . . . . . . . . . . 36
Задачи для контрольных работ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .44
Контрольная работа №1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
Контрольная работа №2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
Контрольная работа №3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Контрольная работа №4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
Приложения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
Российской Федерации
Красноярский государственный аграрный университет
МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ
ЗАДАНИЯ ДЛЯ СТУДЕНТОВ-ЗАОЧНИКОВ
КРАСНОЯРСК 2016
Составитель: Миронов Г.В.
Миронов Г.В. "МАТЕМАТИКА". Методические указания по выполнению контрольных работ и прохождению промежуточного контроля для студентов заочной формы обучения по направлению подготовки Землеустройство и кадастры ‒ бакалавриат 21.03.02 Института ЗКиП. Краснояр. гос. аграр. ун-т.- Красноярск, 2016. с.
Введение
В соответствии с действующими учебным планом студенты-заочники изучают курс высшей математики в течении двух лет и выполняют на каждом курсе по две контрольные работы.
Контрольные работы №1 и №2 выполняются студентами на первом курсе.
Контрольные работы №3 и №4 выполняются на втором курсе.
При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Каждая работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр, номер контрольной работы.
2. Контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условие.
3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем.
4. Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единицей измерения. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах.
5. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
6. Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме.
Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена
7. Получив из института прорецензированную работу (как зачтенную, так и незачтенную), студент должен исправить все отмеченные рецензентом ошибки и недочеты. В случае незачета по работе студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
8. В межсессионный период или во время лабораторно-экзаменационной сессии студент должен пройти на кафедре высшей математики собеседование по зачтенной контрольной работе.
9. Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра. При этом, если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1. если предпоследняя цифра учебного шифра есть число четное или ноль (2, 4, 6, 8, 0), то номера задач даны в таблице 2.
Таблица 1
| Номер варианта | Номера задач для контрольных работ | |||||||||||||||
|
Работа №1 |
Работа №2 | |||||||||||||||
| 1 | 1 | 21 | 31 | 41 | 51 | 61 | 81 | 101 | 121 | 131 | 141 | 161 | ||||
| 2 | 2 | 22 | 32 | 42 | 52 | 62 | 82 | 102 | 122 | 132 | 142 | 162 | ||||
| 3 | 3 | 23 | 33 | 43 | 53 | 63 | 83 | 103 | 123 | 133 | 143 | 163 | ||||
| 4 | 4 | 24 | 34 | 44 | 54 | 64 | 84 | 104 | 124 | 134 | 144 | 164 | ||||
| 5 | 5 | 25 | 35 | 45 | 55 | 65 | 85 | 105 | 125 | 135 | 145 | 165 | ||||
| 6 | 6 | 26 | 36 | 46 | 56 | 66 | 86 | 106 | 126 | 136 | 146 | 166 | ||||
| 7 | 7 | 27 | 37 | 47 | 57 | 67 | 87 | 107 | 127 | 137 | 147 | 167 | ||||
| 8 | 8 | 28 | 38 | 48 | 58 | 68 | 88 | 108 | 128 | 138 | 148 | 168 | ||||
| 9 | 9 | 29 | 39 | 49 | 59 | 69 | 89 | 109 | 129 | 139 | 149 | 169 | ||||
| 0 | 10 | 30 | 40 | 50 | 60 | 70 | 90 | 110 | 130 | 140 | 150 | 170 | ||||
|
Работа №3 |
Работа №4 | |||||||||||||||
| 1 | 181 | 191 | 201 | 211 | 231 | 251 | 271 | 281 | 291 | 301 | 311 | |||||
| 2 | 182 | 192 | 202 | 212 | 232 | 252 | 272 | 282 | 292 | 302 | 312 | |||||
| 3 | 183 | 193 | 203 | 213 | 233 | 253 | 273 | 283 | 293 | 303 | 313 | |||||
| 4 | 184 | 194 | 204 | 214 | 234 | 254 | 274 | 284 | 294 | 304 | 314 | |||||
| 5 | 185 | 195 | 205 | 215 | 235 | 255 | 275 | 285 | 295 | 305 | 315 | |||||
| 6 | 186 | 196 | 206 | 216 | 236 | 256 | 276 | 286 | 296 | 306 | 316 | |||||
| 7 | 187 | 197 | 207 | 217 | 237 | 257 | 277 | 287 | 297 | 307 | 317 | |||||
| 8 | 188 | 198 | 208 | 218 | 238 | 258 | 278 | 288 | 298 | 308 | 318 | |||||
| 9 | 189 | 199 | 209 | 219 | 239 | 259 | 279 | 289 | 299 | 309 | 319 | |||||
| 0 | 190 | 200 | 210 | 220 | 240 | 260 | 280 | 290 | 300 | 310 | 320 | |||||
Таблица 2
| Номер варианта | Номера задач для контрольных работ | |||||||||||||||
|
Работа №1 |
Работа №2 | |||||||||||||||
| 1 | 11 | 22 | 33 | 44 | 55 | 76 | 91 | 111 | 122 | 133 | 151 | 171 | ||||
| 2 | 12 | 23 | 34 | 45 | 56 | 77 | 92 | 112 | 123 | 134 | 152 | 172 | ||||
| 3 | 13 | 24 | 35 | 46 | 57 | 78 | 93 | 113 | 124 | 135 | 153 | 173 | ||||
| 4 | 14 | 25 | 36 | 47 | 58 | 79 | 94 | 114 | 125 | 136 | 154 | 174 | ||||
| 5 | 15 | 26 | 37 | 48 | 59 | 80 | 95 | 115 | 126 | 137 | 155 | 175 | ||||
| 6 | 16 | 27 | 38 | 49 | 60 | 71 | 96 | 116 | 127 | 138 | 156 | 176 | ||||
| 7 | 17 | 28 | 39 | 50 | 51 | 72 | 97 | 117 | 128 | 139 | 157 | 177 | ||||
| 8 | 18 | 29 | 40 | 41 | 52 | 73 | 98 | 118 | 129 | 140 | 158 | 178 | ||||
| 9 | 19 | 30 | 31 | 42 | 53 | 74 | 99 | 119 | 130 | 131 | 159 | 179 | ||||
| 0 | 20 | 21 | 32 | 43 | 54 | 75 | 100 | 120 | 121 | 132 | 160 | 180 | ||||
|
Работа №3 |
Работа №4 | |||||||||||||||
| 1 | 182 | 193 | 204 | 221 | 241 | 261 | 272 | 283 | 294 | 305 | 316 | |||||
| 2 | 183 | 194 | 205 | 222 | 242 | 262 | 273 | 284 | 295 | 306 | 317 | |||||
| 3 | 184 | 195 | 206 | 223 | 243 | 263 | 274 | 285 | 296 | 307 | 318 | |||||
| 4 | 185 | 196 | 207 | 224 | 244 | 264 | 275 | 286 | 297 | 308 | 319 | |||||
| 5 | 186 | 197 | 208 | 225 | 245 | 265 | 276 | 287 | 298 | 309 | 320 | |||||
| 6 | 187 | 198 | 209 | 226 | 246 | 266 | 277 | 288 | 299 | 310 | 311 | |||||
| 7 | 188 | 199 | 210 | 227 | 247 | 267 | 278 | 289 | 300 | 301 | 312 | |||||
| 8 | 189 | 200 | 201 | 228 | 248 | 268 | 279 | 290 | 291 | 302 | 313 | |||||
| 9 | 190 | 191 | 202 | 229 | 249 | 269 | 280 | 281 | 292 | 303 | 314 | |||||
| 0 | 181 | 192 | 203 | 230 | 250 | 270 | 271 | 282 | 293 | 304 | 315 | |||||
СОДЕРЖАНИЕ ПРОГРАММЫ
Дата: 2018-12-21, просмотров: 378.