Прогноз погоды на любом из телевизионных каналов: завтра температура воздуха +5°С, возможен дождь. В этом случае даже профессиональные синоп- тики не могут точно сказать будет дождь или нет. Это и есть проявление нечет- кой логики: погода завтра может быть в данном случае как просто пасмурной, так и дождливой: события здесь предсказываются с некоторой долей уверенно- сти (рангом).

Рассмотрим теперь другой пример, связанный с возрастом человека (ри-

сунок 2). До 16 лет нельзя однозначно утверждать, что человек молодой (на-

пример, 15-летие относится к термину молодой с рангом около 0,9). Зато диапазону от 16 до 30 лет можно смело присвоить ранг 1, т.е. человек в этом возрасте молодой. После 30 лет человек вроде уже не молодой, но еще и не ста- рый, здесь принадлежность (ранг) термина молодой возрасту будет принимать значения в интервале от 0 до 1. И чем больше возраст человека, тем меньше

становится его принадлежность к молодым, т.е. ранг будет стремиться к 0.

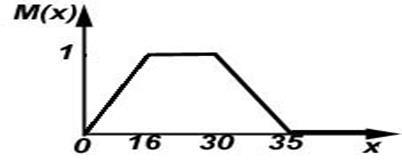
Рисунок 3.2 - Нечеткое множество для термина молодой.

Рассуждая таким образом, было получено нечеткое множество, описы- вающее понятие молодости для всего диапазона возрастов человека. Если вве- сти остальные термины (например, очень молодой, старый и т.д.), то можно охарактеризовать такую переменную как возраст, состоящую из нескольких не- четких множеств и полностью перекрывающую весь жизненный период.

К нечетким множествам можно применять следующие операции:

1. объединение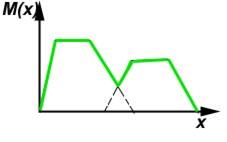                                     

2. пересечение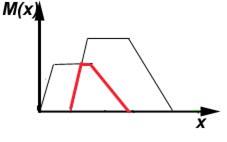                                      

3. дополнение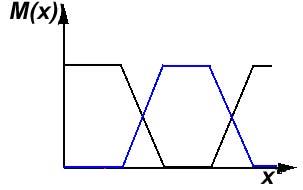                            

4. концентрация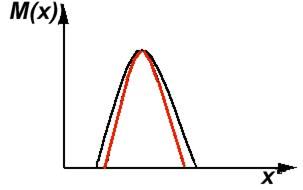                           

Рисунок 3.3 - Операции, применяемые к нечетким множествам

Фаззификация - сопоставление множества значений х ее функции при- надлежности М(х), т.е. перевод значений х в нечеткий формат (пример с термином молодой).

Дефаззификация - процесс, обратный фаззификации.

Все системы с нечеткой логикой функционируют по одному принципу: фактические данные фаззифицируются (переводятся в нечеткий формат), обра- батываются (см. ниже), дефаззифицируются и в виде управленческих решений подаются на исполнительные устройства.

Степень принадлежности - это не вероятность, т.к. неизвестна функция распределения, нет повторяемости экспериментов. Так, если взять из рассмот- ренного ранее примера прогноза погоды два взаимоисключающих события: бу- дет дождь и не будет и присвоить им некоторые ранги, то сумма этих рангов необязательно будет равна 1, но если равенство все-таки есть, то нечеткое мно- жество считается нормированным. Значения функции принадлежности M(x) могут быть взяты только из априорных знаний, интуиции (опыта), опроса экс- пертов.

В нечеткой логике вводится понятие лингвистической переменной, зна- чениями которой являются не числа, а слова естественного языка, называемые термами.