Если матрица А системы линейных уравнений невырожденная, т.е. det A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A1B называют матричным способом решения системы, или решением по методу обратной матрицы.
Пример 2.15. Решить матричным способом систему уравнений
x1 - x2 + x3 = 6,
2x1 + x2 + x3 = 3,
x1 + x2 +2x3 = 5.
Решение. Обозначим

Тогда данная система уравнений запишется матричным уравнением AX=B. Поскольку 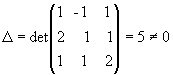 ,
,
то матрица A невырожденная и поэтому имеет обратную:
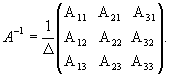 .
.
Для получения решения X мы должны умножить вектор-столбец B слева на матрицу A: X = A-1B. В данном случае
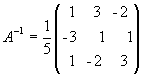
и, следовательно,
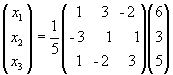 .
.
Выполняя действия над матрицами, получим:
x1 = 1/5(1×6+3×3-2×5) = 1/5 (6+9-10) = 1,
x2 = 1/5 (-3×6 +1×3 - 1×5) = 1/5 (- 18 + 3 + 5) = -2,
x3 = 1/5 (1×6 - 2×3 + 3×5) = 1/5 (6 -6 + 15) = 3.
Ответ: (1, -2, 3)
Метод Гаусса (последовательного исключения неизвестных)
Сначала систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений.
Рассмотрим простейшую систему уравнений 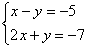
и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы:
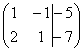 .
.
Справка: Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы : 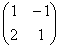 .
.
Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: 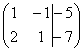 .
.
Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: 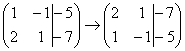
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу  .
.
В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: 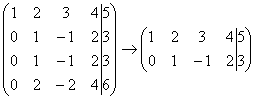 .
.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить.
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу 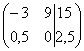 .
.
Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: 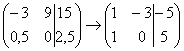 .
.
Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: 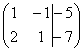 .
.
Умножаем первую строку на -2: 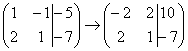 ,
,
и ко второй строке прибавляем первую строку, умноженную на –2:
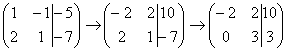 .
.
Теперь первую строку можно разделить «обратно» на –2:
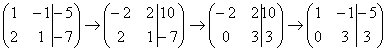 .
.
Строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
На практике так подробно, конечно, не расписывают, а пишут короче:
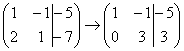
Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: 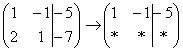 »
»
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: 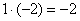 , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку:
, и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: 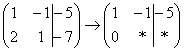 »
»
«Теперь второй столбец. Вверху –1 умножаю на –2: 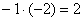 . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку:
. Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: 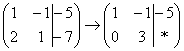 »
»
«И третий столбец. Вверху –5 умножаю на –2: 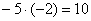 . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку:
. Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: 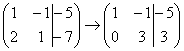 »
»
Вернемся к нашей системе 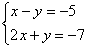 . Она уже почти решена.
. Она уже почти решена.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
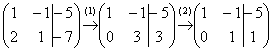
(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: 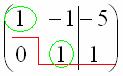 . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.
. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.
В результате элементарных преобразований получена эквивалентная исходной система уравнений:
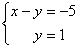
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.
В нижнем уравнении у нас уже готовый результат: 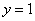 .
.
Рассмотрим первое уравнение системы 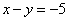 и подставим в него уже известное значение «игрек»:
и подставим в него уже известное значение «игрек»:
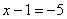

Ответ: 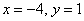
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример
Решить методом Гаусса систему уравнений:
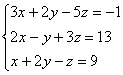
Запишем расширенную матрицу системы:
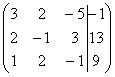
Результат, к которому мы придём в ходе решения:
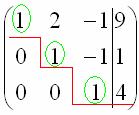
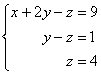
В третьем уравнении у нас уже готовый результат: 
Смотрим на второе уравнение: 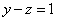 . Значение «зет» уже известно, таким образом:
. Значение «зет» уже известно, таким образом:
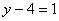
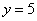
И, наконец, первое уравнение: 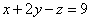 . «Игрек» и «зет» известны, дело за малым:
. «Игрек» и «зет» известны, дело за малым:
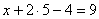
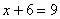
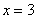
Ответ:
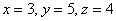
ТЕМА: ЭЛЕМЕНТЫ ТЕОРИЯ ВЕРОЯТНОСТЕЙ ИМАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Определение. Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу всех исходов (несовместимых, единственно возможных и равновозможных), т.е.
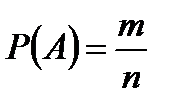
Это равенство называют обычно классическим определением вероятности.
Если в задаче говорится, что выбор производится наугад, наудачу, случайным образом, то это означает, что его элементарные исходы равновозможны.
ПРИМЕР. Из цифр от 1 до 9 включительно наугад выбирается одна. Найти вероятность того, что выбранное число будет простым.
Решение:
1. Опыт состоит в выборе одной цифры.
2. Пространство элементарных исходов:
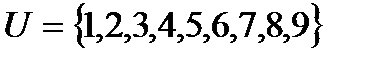
3. Исходы опыта равновозможны, т.к. выбор производится наугад.
4. Количество всех исходов n = 9.
5. Событие А – «выбранное число простое».
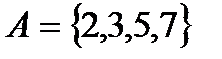
6. Число исходов, благоприятствующих наступлению события А: m = 4.
7. Найдем вероятность события
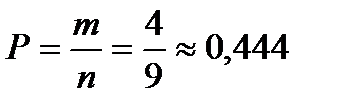
Ответ: вероятность того, выбранное число будет простым равна 4/9 (0,444).
Дата: 2018-12-21, просмотров: 324.