В предыдущем разделе мы узнали, что всякое число может быть выражено в сотых долях, то есть в виде процентов. Теперь ставится обратная задача: выразить проценты в виде десятичной дроби. Например, 9 % означают 9 сотых долей. Записать это можно так: 9 % = 9/100 = 0,09. По аналогии выводим:
37 % = 37/100 = 0,37; 600 % = 600/100 = 6; 290 % = 290/100 = 2,9.
Чтобы выразить процент десятичной дробью или натуральным числом, нужно число, стоящее перед знаком %, разделить на 100.
Например:
58 % = 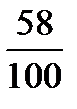 = 0,58
= 0,58
Это правило можно сформулировать и так: чтобы проценты выразить в виде десятичной дроби, надо в их числе перенести запятую на два знака влево.
Примеры: 300 % = 3; 36,7 % = 0,367; 9 % = 0,09; 0,1= 0,001
Нахождение процентов от данного числа
Задача. В семенах сои содержится 20 % масла. Сколько масла содержится в 700 кг сои?
Решение.
В задаче требуется найти указанную часть (20 %) от известной величины (700 кг). Такие задачи можно решать способом приведения к единице. Основное значение величины – 700 кг. Её мы можем принять за условную единицу. А условная единица и есть 100 %.
Кратко условия задачи можно записать так:
700 кг – 100 %
Х кг – 20 %.
Здесь за Х принята искомая масса масла. Узнаем, какая масса сои приходится на 1 %. Поскольку на 100 % приходится 700 кг, то на 1 % будет приходиться масса, в сто раз меньшая, то есть 700 : 100 = 7 (кг). Значит, на 20 % будет приходиться в 20 раз больше: 7 х 20 = 140 (кг). Следовательно, в 700 кг сои содержится 140 кг масла.
Эту задачу можно решить и иначе. Если в условие этой задачи вместо
20 % написать равное ему число 0,2, то получим задачу на нахождение дроби от числа. А такие задачи решают умножением. Отсюда получим другой способ решения:
1) 20 % = 0,2; 2) 700 х 0,2 = 140 (кг).
Чтобы найти несколько процентов от числа, надо проценты выразить дробью, а затем найти дробь от данного числа.
Нахождение числа по его процентам
Задача. Из хлопка-сырца получается 24 % волокна. Сколько надо взять хлопка-сырца, чтобы получить 480 кг волокна?
Решение
480 кг волокна составляют 24 % от некоторой массы хлопка-сырца, которую примем за Х кг. Будем считать, что Х кг составляют 100 %. Теперь кратко условие задачи можно записать так:
480 кг - 24 %
Х кг - 100 %
Решим эту задачу способом приведения к единице. Узнаем, какая масса волокна приходится на 1 %. Поскольку на 24 % приходится 480 кг, то, очевидно, на 1 % будет приходиться масса в 24 раза меньше, то есть 480 : 24 = = 20 (кг). Далее рассуждаем так: если на 1 % приходится масса в 20 кг, то на 100 % будет приходиться масса, в 100 раз большая, то есть 20 х 100 = 2000 (кг)
= 2 (т). Следовательно, для получения 480 кг волокна надо взять 2 т хлопка-сырца.
Эту задачу можно решить и иначе.
Если в условии этой задачи вместо 24 % написать равное ему число 0,24, то получим задачу на нахождение числа по известной его части (дроби). А такие задачи решают делением. Отсюда вытекает ещё один способ решения:
1) 24 % = 0,24; 2) 480 : 0,24 = 2000 (кг) = 2 (т).
Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби и решить задачу на нахождение числа по данной его дроби.
Процентное отношение двух чисел
Задача 1. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?
Решение
Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить его отношение в процентах:
150/500 = 3/10 = 0,3 = 30 %
Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).
Чтобы найти процентное отношение двух чисел, надо найти отношение этих чисел и выразить его в процентах.
Задача 2. Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?
Решение
Для ответа на вопрос задачи надо найти отношение (частное) числа 45 к 36 и выразить его в процентах:
45 : 36 = 1,25 = 125 %.
Проценты в банковской системе
Простой процентный рост.
Если человек не вносит своевременную плату за квартиру, то на него налагается штраф, который называется «пеня». Так в Москве пеня составляет 1% от суммы квартплаты за каждый день просрочки. Поэтому, например, за 19 дней просрочки, сумма составит 19% от суммы квартплаты, и в месте , скажем, со 100 руб. квартплаты человек должен будет внести пеню 0,19 * 100 = 19 руб., а всего 119 руб.
Ясно, что в разных городах и у разных людей, квартплата, размер пани и время просрочки разные. Поэтому имеет смысл, составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.
Пусть S – ежемесячная кварт плата, пеня составляет p% квартплаты за каждый день просрочки, а n – число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим Sn.
Тогда за n дней просрочки, пеня составит pn% от S , или 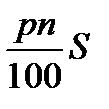 , а всего придётся заплатить
, а всего придётся заплатить 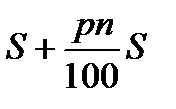 .Таким образом,
.Таким образом,
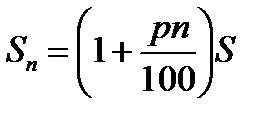
Задача 1. Сколько надо заплатить москвичу, если его квартплата составляет 100 руб. и просрочена на 5 дней?
Решение.
Подставляя в формулу значение p = 1 и значения n = 5 * 4, получим:
(1 + 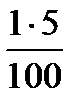 ) * 100 = 1,05 * 100 = 105 (руб.)
) * 100 = 1,05 * 100 = 105 (руб.)
Ответ: через 5 дней – 105 руб.
Таким образом, установленная формула позволяет быстро рассчитывать необходимые значения выплат за квартиру.
Рассмотрим еще одну ситуацию. Банк выплачивает вкладчикам каждый месяц p% от внесенной суммы. Поэтому, если клиент внес сумму S, то через n месяцев на его счете будет ( 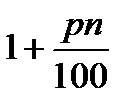 )S, и мы вновь получаем, что
)S, и мы вновь получаем, что
Sn=(1+ 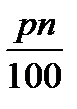 ) S
) S
Мы получили в точности ту же самую формулу, что и в примере с квартплатой, хотя буквы в этих двух примерах имеют разный смысл: в первом примере n – число дней, а во втором примере n - число месяцев, в первом примере S – величина квартплаты, а во втором S – сумма, внесенная в банк. Такая же формула будет получаться и во всех иных случаях, когда некоторая величина увеличивается на постоянное число процентов за каждый фиксированный период времени. Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.
Задача 2. Банк выплачивает вкладчикам каждый месяц 2% от внесённой суммы. Клиент сделал вклад в размере 500 рублей. Какая сумма будет на его счёте через полгода?
Решение.
Для решения задачи достаточно подставить в формулу величину процентной ставки p = 2, числа месяцев n = 6 и первоначального вклада S = 500:
(1 + 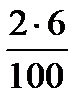 ) * 500 = 1,12 * 500 = 560 (руб.)
) * 500 = 1,12 * 500 = 560 (руб.)
Ответ: через полгода на вкладе будет 560 руб.
Сложный процентный рост
В Сберегательном банке России для некоторых видов вкладов принята следующая система начисления денег. За первый год нахождения внесенной суммы на счете начисляется 40% от нее. В конце года вкладчик может снять со счета эти деньги – «проценты», как их обычно называют.
Если же он этого не сделал, то они присоединяются к начальному вкладу, и поэтому в конце следующего года 40% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.
Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк1000 руб. и ни разу не будет брать деньги со счета:
40% от 1000 руб. составляют 0,4 * 1000 = 400 руб., и следовательно, через год на его счете будет
1000 + 400 = 1400 (руб.)
40% от новой суммы 1400 руб. составляют 0,4 * 1400 = 560 руб., и следовательно, через 2 года на его счете будет
1400 + 560 = 1960 (руб.)
40% от новой суммы 1960 руб. составляют 0,4 * 1960 = 784 руб., и следовательно, через 3 года на его счете будет
1960 + 784 = 2744 (руб.)
Нетрудно представить себе, сколько при таком непосредственном , «лобовом» подсчёте понадобилось бы времени для нахождения суммы вклада через 10 лет. Между тем, подсчёт можно вести значительно проще.
Именно через год начальная сумма увеличится на 40%, то есть составит 140% от начальной, или, другими словами, увеличится в 1,4 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 40%. Следовательно, через 2 года начальная сумма увеличится в 1,4 * 1,4 = 1,42 раза.
Еще через один год и эта сумма увеличится в 1,4 раза, так что начальная сумма увеличится в 1,4 * 1,42 = 1,43 раза. При таком способе рассуждения получаем решение нашей задачи значительно более простое:
1,43 * 1000 = 2,744 * 1000 = 2744 (руб.)
Решим теперь эту задачу в общем виде. Пусть банк начисляет p% годовых, внесённая сумма равна S рублей, а сумма, которая будет на счёте через n лет, равна Sn рублей.
p% от S составляют 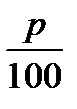 S рублей, и через год на счёте окажется сумма
S рублей, и через год на счёте окажется сумма
S1 = 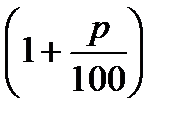 S
S
то есть начальная сумма увеличится в 1 + 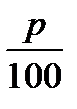 раза.
раза.
За следующий год сумма S1 увеличится во столько же раз, и поэтому через два года на счёте будет сумма
S2 = (1 + 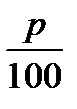 ) S1 = (1 +
) S1 = (1 + 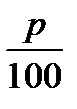 ) (1+
) (1+ 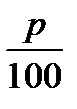 ) S =(1 +
) S =(1 + 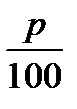 )2 S.
)2 S.
Аналогично, S3 =(1 + 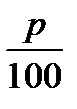 )3 S и так далее. Другими словами, справедливо равенство
)3 S и так далее. Другими словами, справедливо равенство
Sn = (1 + 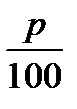 ) 3 S.
) 3 S.
Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.
Задача 1. Какая сумма будет на срочном счёте вкладчика через 4 года, если банк начисляет 10% годовых и внесённая сумма равна 2 000 рублей?
Решение.
Подставим в формулу значения процентной ставки p = 10, количество лет n = 4 и величину первоначального вклада S = 2000, получим:
(1 + 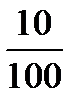 )4 * 2000 = 1,14 * 2000 = 1,4641 * 2000 = 2928,2 (рублей).
)4 * 2000 = 1,14 * 2000 = 1,4641 * 2000 = 2928,2 (рублей).
Ответ: через 4 года на счёте будет сумма 2928,2 рубля.
ТЕМА: ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА
Найти производные от функций:
а) 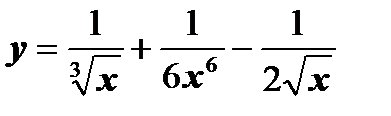 ; ;
| б) 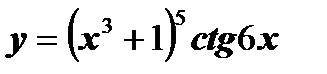 ; ;
| в) 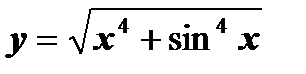 ; ;
|
г) 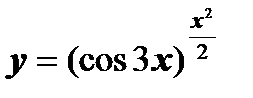
| д) 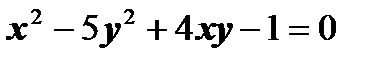 ; ;
| е) 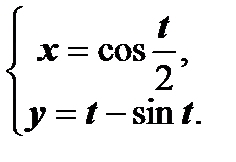
|
Решение. При решении заданий а)-в) применим следующие правила дифференцирования:
1) 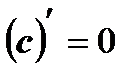 ; 2)
; 2) 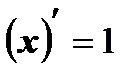 ;
;
3) 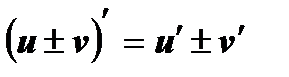 ; 4)
; 4) 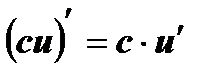
5) 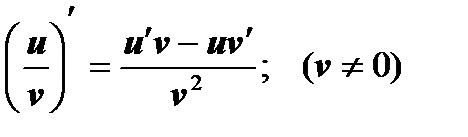 6)
6) 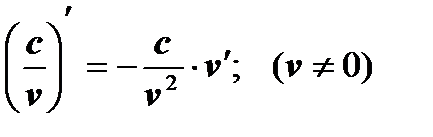
7) 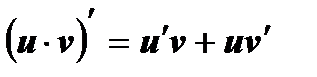 ;
;
8) если 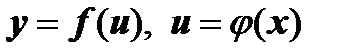 , т.е.
, т.е. 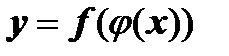 - сложная функция, то
- сложная функция, то 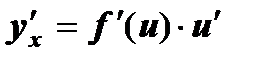 .
.
На основании определения производной и правил дифференцирования составлена таблица производных основных элементарных функций.
1 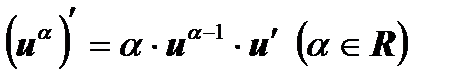 , ,
| 8 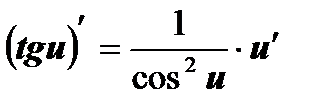 , ,
|
2 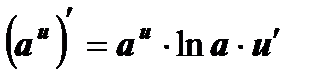 , ,
| 9 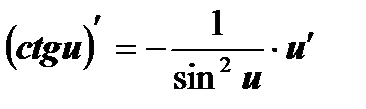 , ,
|
3 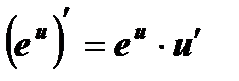 , ,
| 10 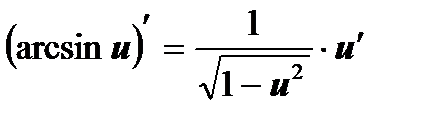 , ,
|
4 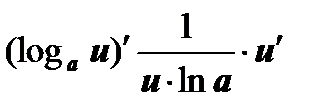 , ,
| 11 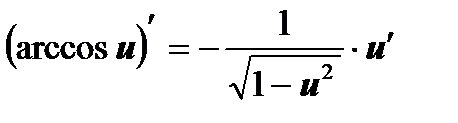 , ,
|
5 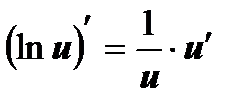 , ,
| 12 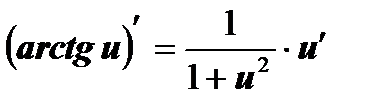 , ,
|
6 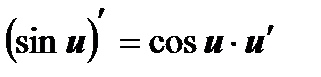 , ,
| 13 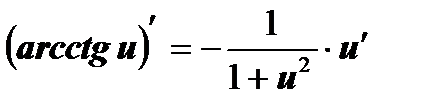 . .
|
7 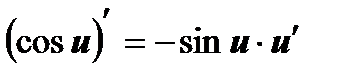 , ,
|
Используя правила дифференцирования и таблицу производных, найдем производные данных функций:
а)  .
.
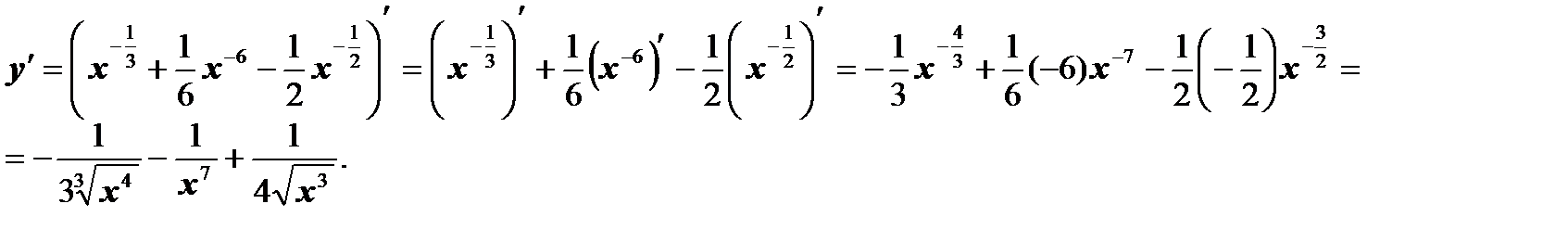
Ответ: 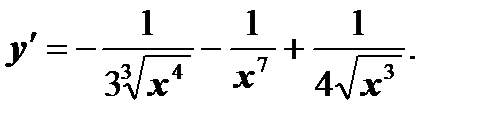
б) 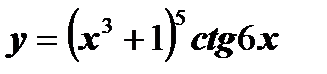 .
.
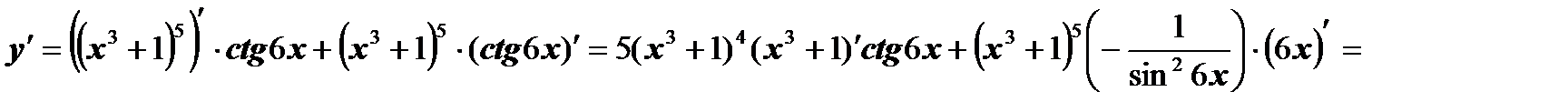
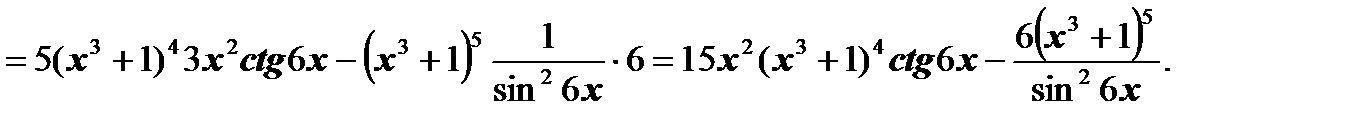
Ответ: 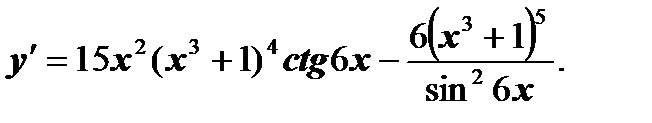
в) 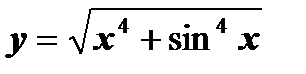 .
.
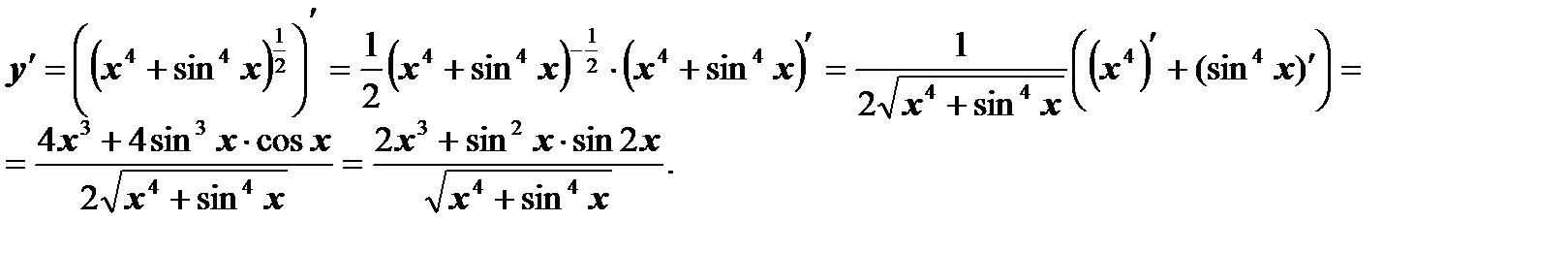
Ответ: 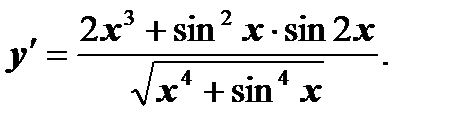
ТЕМА: НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Дата: 2018-12-21, просмотров: 474.