Между четырьмя основными видами простых суждений устанавливаются следующие отношения:
1) Отношение подчинения;
2) Отношение противоположности (контрарность);
3) Отношение частичной совместимости (подпротивоположности);
4) Отношение противоречия (контрадикторность).
Обычно эти виды отношений между суждениями характеризуют с помощью схемы, получившей название «логического квадрата».
А Е
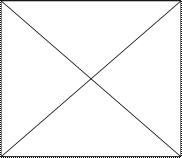 |
I О
Отношения подчинения возникают между суждениями A – I, E – O. Суждения A, E - подчиняющие, а суждения I, O - подчиненные. Если общее суждение истинно, то истинным является и частное суждение.
Отношения противоположности возникают между суждениями A – E. Данные суждения не могут одновременно быть истинными, но могут одновременно быть ложными.
Отношения частичной совместимости возникают между суждениями I – O. Эти суждения могут быть одновременно истинными, но не могут быть одновременно ложными.
Отношения противоречия возникают между суждениями A – O, E – I, различающимися качеством и количеством. Они характеризуются тем, что не могут быть одновременно истинными или одновременно ложными. Если истинно одно, то другое обязательно ложно, и наоборот.
СЛОЖНЫЕ СУЖДЕНИЯ
Сложные суждения состоят из простых, объединенных логическими союзами. Входящие в сложное суждение простые суждения являются, собственно, логическими переменными, которые можно обозначить как a, b, c…
Логических союзов несколько:
- конъюнкция - /\ (в языке данному логическому союзу соответствуют грамматические союзы «и», «а», «да», «но», «хотя», «зато» и некоторые другие, а также запятая, точка с запятой, тире);
- дизъюнкция строгая - \/ (выражается грамматическим союзом «или-или», «либо-либо», т. е. предъявляется требование выбора - одно из двух и третьего не дано);
- дизъюнкция нестрогая - \/ (выражается грамматическим союзом «или», «либо», можно выбрать один или несколько альтернативных вариантов);
- импликация - → (обозначается грамматическим союзом «если…то»).
- эквиваленция - ↔ (выражается словами «…тогда и только тогда, когда…»).
- отрицание (отсутствие связи между какими-либо объектами) -ù (выражается словами «неверно, что…», «не-»).
По типу применяемого логического союза сложные суждения делятся на:
- конъюнктивные (соединительные);
- дизъюнктивные (исключающе-разделительные и соединительно-разъединительные);
- импликативные (условные).
Приведем примеры.
1) Конъюнктивное высказывание «Прозрачный лес один чернеет, и ель сквозь иней зеленеет, и речка подо льдом блестит» (Пушкин).
Данное сложное суждение состоит из трех простых:
«Прозрачный лес один чернеет» - a
«Ель сквозь иней зеленеет» - b
«Речка подо льдом блестит» - с
Используя знак конъюнкции «/\» получаем символическую запись данного высказывания: a /\ b /\ с читается: a конъюнкция b конъюнкция с.
2) Высказывание строгой дизъюнкции «Амнистия может быть общей либо частичной».
Данное сложное суждение состоит из двух простых:
«Амнистия может быть общей» - a
«Амнистия может быть частичной» - b
Используя знак строгой дизъюнкции «\/» получаем символическую запись данного высказывания: a \/ b, читается: a дизъюнкция b.
3) Импликативное высказывание «Если вода не нагревается, то она не испаряется».
«Вода не нагревается» - ù a
«Вода не испаряется» - ù b
Используя знак импликации « → » получаем символическую запись данного высказывания: ù (a → b), читается: неверно, что a имплицирует b.
4) Комбинированное высказывание «Если служащий нарушил дисциплину (a), то администрация обязана взять у него либо устные (b), либо письменные объяснения(c)».
В символической записи данное высказывание будет выглядеть следующим образом: a → (b \/ c).
См. задание 8 контрольной работы.
Классификацию суждений можно представить в виде схемы (см. табл. 2).
Таблица 2
Классификация суждений
| Основные деления суждений | Виды суждений |
| 1. Состав суждений | Простые Сложные |
| 2. По типу применяемого логического союза в сложных суждениях | Конъюнктивные (соединительные) Дизъюнктивные (исключающе-разделительные, соединительно-разделительные) Импликативные (условные) |
| 3. По качеству (от характера логической связки в простых суждениях) | Утвердительные Отрицательные |
| 4. По количеству (в зависимости от того, относится ли S к одному предмету, некоторым предметам или целому классу предметов) | Общие (квантор общности) Частные (квантор существования) Единичные (квантор единичности) |
| 5. Объединенная классификация по качеству и количеству | Общеутвердительные (А) Частноутвердительные (I) Общеотрицательные (Е) Частноотрицательные (О) |
| 6. По объективной модальности | Возможности Действительности Необходимости |
| 7. По логической модальности | Вероятные Достоверные |
ОСНОВНЫЕ ЗАКОНЫ ФОРМАЛЬНОЙ ЛОГИКИ
Логический закон - это необходимая, устойчивая, повторяющаяся связь между мыслями.
Наиболее простые и необходимые связи между мыслями выражаются в основных формально-логических законах:
1. закон тождества;
2. закон непротиворечия;
3. закон исключенного третьего;
4. закон достаточного основания.
Закон тождества
Мысль должна быть тождественна самой себе, т.е. закон тождества требует, чтобы 1) рассуждая об известном предмете, мы рассуждали именно о нем, а не о другом предмете; 2) включая мысль о предмете в наши рассуждения, мы мыслили этот предмет по одним и тем же признакам.
Запрет отождествления различных мыслей представляется очевидным, хотя в процессе рассуждения он нередко нарушается. Это связано с тем, что любая мысль выражается в языке, причем одна и та же мысль может быть выражена по-разному. Например, «Капитан милиции Павлов родился в 1961 году» и «Капитан милиции Павлов родился в год первого космического полета человека».
Привести к ошибочному отождествлению различных мыслей может употребление многозначных слов и слов - синонимов и омонимов. Поэтому, нужно употреблять слово в таких сочетаниях, которые делают его однозначным.
Закон непротиворечия
Мысль противоречива, если мы об одном и том же предмете в одно и то же время и в одном и том же отношении нечто утверждаем и то же самое отрицаем. Например: «Кама - приток Волги» и «Кама не является притоком Волги». Одно из противоположных высказываний необходимо ложно, но ложными могут быть оба. Например: «Все дежурные части линейных отделений милиции оборудованы современными компьютерами» и « Ни одна из дежурных частей линейных отделений милиции современными компьютерами не оборудована». Скорее всего, истинным будет высказывание: «Некоторые дежурные части линейных отделений милиции оборудованы/не оборудованы современными компьютерам».
Таким образом, закон не определяет, чья точка зрения ложна, закон лишь утверждает, что кто-то из оппонентов неправ или неправы оба.
Противоречия не будет, если мы говорим о разных предметах или об одном и том же предмете, взятом в разное время или в разном отношении. Например: «Осенью дождь полезен для грибов» и «Осенью дождь не полезен для уборки урожая».
Действие закона непротиворечия проявляется в стремлении разрешать возникшие противоречия путем уточнения мысли, более строго определяя понятия, отказываясь от некоторых предпосылок.
Закон непротиворечия справедлив относительно противоположных и противоречащих друг другу высказываний.
Закон исключенного третьего
Из двух взаимоисключающих суждений одно истинно, другое ложно, а третьего не дано.
Закон исключенного третьего распространяется только на противоречащие друг другу суждения. Причем закон не только говорит, что одно из протворечащих утверждений необходимо должно быть истинным, но, кроме того, истина лежит в пределах этих двух высказываний. Например: «Следствие по делу К. закончено» либо «Следствие по делу К. не закончено» (и третьего не дано).
Закон достаточного основания
Всякая истинная мысль должна быть достаточно обоснованной.
Согласно этому закону для того, чтобы признать высказывание о предмете истинным, должно быть указано достаточное основание. Достаточным основанием мыслей может быть личный опыт человека, предшествующий опыт других людей, всего человечества, а также любая уже проверенная и признанная истинной мысль, из которой с необходимостью вытекает истинность данной мысли.
Под достаточным основанием истинности некоторого высказывания вообще понимается совокупность истинных высказываний, таких, что обосновываемое высказывание следует из них по законам и правилам логики.
Например, мы говорим: «Перчатку потерять - к несчастью. Зеркало разбить - к худу». Здесь налицо нарушение закона достаточного основания, так как ни наукой, ни, собственно, личным опытом не установлена логическая связь между перчаткой, зеркалом и несчастьем. Причиной последнего, равно может стать невнимательность, плохое самочувствие, неверно принятое решение и др.
Итак, закон тождества характеризует определенность логического мышления, законы непротиворечия и исключенного третьего - его последовательность, а закон достаточного основания - обоснованность логического мышления.
См. задание 9 контрольной работы.
УМОЗАКЛЮЧЕНИЕ
Умозаключение - это логический процесс выведения нового суждения из одного или более известных ранее суждений.
Суждения, из которых делается вывод, называются посылками умозаключения.
Суждение, являющееся выводом умозаключения, принято называть заключением.
По характеру выводного знания, умозаключения делятся на необходимые и правдоподобные.
Необходимые (или дедуктивные) умозаключения - такие, в которых из истинных посылок с необходимостью выводится истинное умозаключение, достаточно только выполнить определенные правила вывода.
Правдоподобные умозаключения (вероятностные) - такие, в которых из истинных посылок истинное заключение выводится лишь с определенной степенью вероятности.
Необходимые (дедуктивные) умозаключения по числу посылок делятся на непосредственные (одна посылка) и опосредствованные (более, чем одна).
НЕПОСРЕДСТВЕННЫЕ УМОЗАКЛЮЧЕНИЯ
К непосредственным умозаключениям относятся: обращение, превращение, противопоставление предикату, умозаключение по логическому квадрату.
Обратить суждение - значит установить отношение объема предиката к объему субъекта на основании известного отношения субъекта к предикату (т.е. субъект и предикат исходного суждения меняются местами).
Главное правило: если в исходном суждении какой-то термин не распределен, то он таким должен остаться и в заключении. Поэтому обращения бывают либо с ограничением, либо без ограничения.
Суждения типа А, Е, I обращаются соответственно в суждения I, E, I.
Схематически это будет выглядеть следующим образом:

 А Все S есть Р Р‾
А Все S есть Р Р‾
-------------------------------- S+
I Некоторые Р есть S


Е Ни одно S не есть Р
-------------------------------- S+ Р+
Е Ни одно Р не есть S

I Некоторые S есть Р
-------------------------------- S‾ Р‾
I Некоторые Р есть S
Частноотрицательное суждение обращению не подлежит, так как предикат в частноотрицательном суждении распределен, и, следовательно, при обращении мы должны получить общеотрицательное заключение, а оно может быть ложным.
Например: Некоторые люди (S) не знают логики (Р)
----------------------------------------------------
Все знающие логику - не люди
Рассмотрим обращение различных видов суждений.

 1. «Некоторые студенты МФЮА (S) - работники суда и прокуратуры (Р)». Отношение S к Р можно выразить в виде схемы:
1. «Некоторые студенты МФЮА (S) - работники суда и прокуратуры (Р)». Отношение S к Р можно выразить в виде схемы:
I Некоторые S есть Р
------------------------------- S‾ Р‾
I Некоторые Р есть S
Значит, некоторые Р есть S, т.е. «Некоторые работники суда и прокуратуры - студенты МФЮА».
2. «Ни один кит (S) - не рыба (Р)».

 Отношение S к Р можно выразить в виде схемы:
Отношение S к Р можно выразить в виде схемы:
Е Ни одно S не есть Р
-------------------------------- S+ Р+
Е Ни одно Р не есть S
Следовательно, получаем суждение Е «Ни одна рыба - не кит».
См. задание 10 контрольной работы.
Превратить суждение - значит, в выводе субъектом оставить субъект исходного суждения, а предикатом - понятие, противоречащее предикату исходного суждения; при этом связка заменяется на противоположную.
Например:
Все преступления (S) являются общественно опасными деяниями (Р)
--------------------------------------------------------------------------------------------------
Ни одно преступление (S) не является не общественно опасным деянием (Р)
Схема А «Все S есть Р» превращается в схему Е «Все S не есть не-Р».
Превращение утвердительных суждений осуществляется путем введения отрицания перед связкой и перед предикатом.
Превращение отрицательных суждений достигается через перенос отрицания из связки в предикат.
Таким образом, при превращении суждений типа А, Е, I, О получаем соответственно E, A, O, I. Схематически это выглядит так:
А Все S есть Р
------------------------------------
Е Ни одно S не есть не-Р
Е Ни одно S не есть Р
---------------------------------
А Все S есть не-Р
I Некоторые S есть Р
---------------------------------------
О Некоторые S не есть не-Р
О Некоторые S не есть Р
--------------------------------------
I Некоторые S есть не-Р
Например, превратим суждение: «Некоторые правительства не являются миролюбивыми» (O).
Схема: О Некоторые S не есть Р
--------------------------------------
I Некоторые S есть не-Р
Следовательно: O Некоторые правительства не являются миролюбивыми
--------------------------------------------------------------------------- I Некоторые правительства являются немиролюбивыми
См. задание 10 контрольной работы.
Противопоставление предикату - это комбинация превращения и обращения. Вначале исходное суждение А «Все S есть P» превращается в E «ни одно S не есть не-P», а затем превращенное обращается в E «Ни одно не-P не есть S».
Противопоставление предикату для различных видов суждений осуществляется так:
А Все S есть Р
--------------------------------
Ни одно не-Р не есть S
Е Ни одно S не есть Р
-----------------------------
Некоторые не-Р есть S
О Некоторые S не есть Р
-------------------------------
Некоторые не-Р есть S
I Из частноутвердительного суждения необходимые
выводы не следуют.
Рассмотрим пример противопоставления предикату: «Все студенты есть учащиеся» (А).
Схема: этап I А Все S есть Р
--------------------------------------
E Ни одно S не есть не-Р
этап II E Ни одно S не есть не-Р
--------------------------------------
E Ни одно не-P не есть S
Следовательно: А Все студенты есть учащиеся
------------------------------------------------------------ E Ни один из студентов не есть не учащийся
E Ни один из студентов не есть не учащийся
-------------------------------------------------------------------
E Ни один из не учащихся не является студентом
См. задание 10 контрольной работы.
Умозаключение по логическому квадрату дается на основе отношений между истинностными значениями суждений видов A, E, I, O. Это известные уже отношения подчинения, противоположности, частичной совместимости, противоречия.
Учитывая, что каждое суждение - A, E, I, O - может находиться в трех отношениях с другими, из него можно сделать три вывода.
Например, при истинности общеутвердительного суждения «Всякий имеет право на защиту» (Аи, где А - вид суждения, и – «истинно») следует, что 1) подчиненное ему «Некоторые обвиняемые имеют право на защиту» будет истинным (Iи); 2) противоположное ему общеотрицательное суждение «Ни один обвиняемый не имеет право на защиту» обязательно будет ложным (Eл, где л -«ложно») и 3) противоречащее «Некоторые обвиняемые не имеют права на защиту» будет ложным (Oл).
В целом истинностные зависимости отношений между суждениями A, E, I, O имеют общий вид (см. табл. 3):
Таблица 3
|
| A | E | I | O | |
| A | 1 0 | - - | 0 ? | 1 ? | 0 1 |
| E | 1 0 | 0 ? | - - | 0 1 | 1 ? |
| I | 1 0 | ? 0 | 0 1 | - - | ? 1 |
| O | 1 0 | 0 1 | ? 0 | ? 1 | - - |
Знак «1» обозначает истинность суждения, знак «0» - ложность суждения. Знак вопроса указывает на неопределенность отношений между суждениями. В каждом конкретном случае вывод будет зависеть от содержания исходного суждения.
Например, два одинаково ложных общеутвердительных суждения: «Все люди есть студенты» (Ал), «Все люди имеют крылья» (Ал) предполагают различные выводы через отношение противоположности. В первом случае противоположное исходному общеотрицательное суждение «Ни один человек не является студентом» тоже будет ложным (Ел), во втором случае противоположное исходному общеотрицательное суждение «Ни один человек не имеет крыльев» будет истинным (Еи).
Рассмотрим пример выведения по логическому квадрату суждений и на основании таблицы установим их истинность или ложность.
Все студенты юридических вузов изучают логику (Аи)
----------------------------------------------------------------------------------
Ни один из студентов юридического вуза не изучает логику (Ел)
Все студенты юридических вузов изучают логику (Аи)
------------------------------------------------------------------------------------
Некоторые студенты юридических вузов не изучают логику (Ол)
Все студенты юридических вузов изучают логику (Аи)
-------------------------------------------------------------------------------
Некоторые студенты юридических вузов изучают логику (I и)
См. задание 10 контрольной работы.
ОПОСРЕДСТВОВАННЫЕ ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
Дата: 2018-12-21, просмотров: 434.