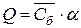1. Цель работы: определение ёмкостей конденсаторов с помощью баллистического гальванометра.
Краткая теория
Взаимодействие зарядов, находящихся на расстоянии друг от друга, осуществляется через электрическое поле. Если в некоторой точке поля заряда q внесён малый положительный заряд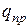 
, называемый «пробный», то на него, по закону Кулона, будет, действовать сила
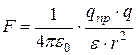. (1)
В этой формуле величина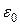 
— электрическая постоянная (в «СИ» единицей измерения 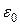является фарада на метр — Ф/м), величина ε — относительная диэлектрическая проницаемость, характеризует электрические свойства среды, в которой взаимодействуют заряды, r — расстояние между зарядами. Отношение 
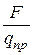не зависит от величины пробного заряда и поэтому может служить характеристикой электростатического поля (т. е. поля, создаваемого неподвижными зарядами). Векторная величина, численно равная силе, действующей на единичный положительный заряд, называется напряженностью электрического поля.
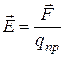. (2)
Из формулы (2), учтя выражение кулоновской силы, получим
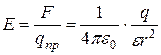. (3)
Как следует из формулы (2), в системе СИ единицей напряженности будет Н/Кл.
Электрическое поле весьма наглядно можно изобразить с помощью силовых линий (линии напряженности).
Силовой линией, электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля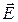 
.
На рис. 18 изображены электрические поля положительного и отрицательного точечного заряда.
Условились силовые линии изображать с такой густотой, чтобы их число, приходящееся па перпендикулярную к ним единицу поверхности, было численно равно напряженности поля.
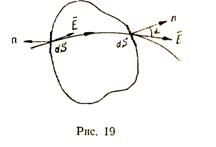
Число силовых линий, пронизывающих некоторую поверхность S, расположенную перпендикулярно к ним, называется потоком напряженности поля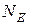 
. Для количества силовых линий, пронизывающих произвольную поверхность
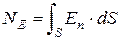, (4)
где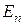 
—проекция вектора 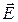на нормаль n к поверхности (рис. 19).
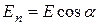, (4*)
где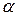 
— угол между вектором 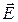и нормалью к поверхности S. Если поле однородное и поверхность плоская, то
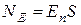. (5)
Напряжённость электрического поля и характеризующая её густота силовых линий изменяются скачком при переходе через границу двух сред с различной диэлектрической проницаемостью (рис. 20). Это создает определённые затруднения при расчёте электрических полей, различных приборов и аппаратов (конденсаторы, кабели и др.). Поэтому вводят вспомогательный вектор
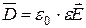. (6)
Вектор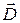 
носит название вектора электрического смещения (вектора индукции). Если подставить в формулу (6) выражение (3), то получим для поля точечного заряда
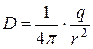. (7)
Легко видеть, что электрическое смещение, в отличие от напряженности, не зависит от свойств среды (рис. 21). В системе СИ электрическое смещение измеряется в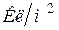 
.
|
|
Большой практический интерес представляет теорема Остроградского-Гаусса. С её помощью можно очень просто определить напряженность полей, создаваемых заряженными телами различной формы. Теорема Остроградского-Гаусса формулируется следующим образом: поток вектора напряжённости электрического поля через замкнутую поверхность равен алгебраической сумме заключённых внутри неё зарядов, делённой на абсолютную диэлектрическую проницаемость, то есть
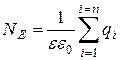, (8)
где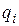 
— заряды, заключённые внутри поверхности.
Рассмотрим два частных случая применения теоремы Остроградского-Гаусса.
1. Определим напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью.
Допустим, поверхностная плотность зарядов плоскости (т. е. заряд, приходящийся на единицу площади) равна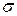 
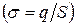
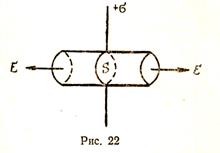
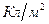. Силовые линии поля бесконечно заряженной плоскости перпендикулярны этой плоскости (рис. 22). Построим воображаемую цилиндрическую поверхность (гауссова поверхность), ось которой перпендикулярна плоскости. Плоскость делит цилиндр пополам. Поток вектора напряжённости проходит только через основания цилиндра, так как линии напряжённости параллельны боковой поверхности цилиндра. Поэтому суммарный поток вектора напряженности будет равен 
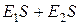(S — площадь основания цилиндра).
По теореме Остроградского-Гаусса имеем:
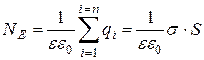(9)
или
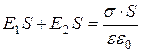. (10)
Учитывая, что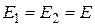 
, получим выражение для напряженности поля бесконечной равномерно заряженной плоскости в системе СИ:
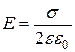. (11)
Таким образом, на любых расстояниях от плоскости напряжённость поля одинаковая по величине. Следовательно, электрическое поле плоскости является однородным.
2.Определим напряженность поля между двумя бесконечными параллельными разноимённо заряженными плоскостями. На рис. 23 поле положительно заряженной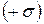 
плоскости изображено сплошными линиями, отрицательно заряженной 
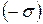плоскости — прерывистыми. Напряжённость поля между двумя бесконечными параллельными плоскостями равна сумме напряжённостей полей, ими создаваемых:
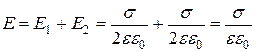. (12)
Слева и справа от плоскостей силовые линии направлены в противоположные стороны и поэтому в пространстве за плоскостями напряженность поля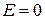 
. Такой же вид имеет поле между параллельными плоскостями конечных размеров. Заметное отклонение поля от однородности имеется только вблизи краев пластин. Система из двух близко расположенных параллельных металлических пластин, разделенных диэлектриком, представляет собой простейший конденсатор. С помощью формулы (12) можно рассчитать напряженность поля внутри плоского конденсатора. Энергетической характеристикой электрического поля является потенциал. Потенциал численно равен работе, которую совершают силы электрического поля над единичным положительным зарядом 
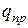при удалении его из данной точки поля в другую, где поле отсутствует (например, в бесконечность)
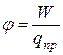. (13)
Работа сил поля по перемещению заряда q из точки (1) в точку (2) поля может быть выражена через разность потенциалов:
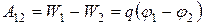. (14)
Согласно формуле (13), потенциал (электрическое напряжение U) в системе СИ измеряется в вольтах
.
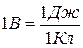Напряжение связано с напряженностью поля Е и расстоянием между пластинами соотношением
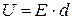. (15)
Напряженность поля между пластинами в соответствии с (12) равна:
.
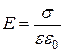Учитывая, что поверхностная плотность зарядов пластины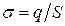 
, можно записать:
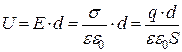, (16)
или
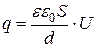. (17)
Из этой формулы следует, что напряжение U, приложенное к пластинам, пропорционально заряду
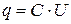. (18)
Коэффициент пропорциональности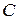 
называется электроёмкостью (сокращённо — ёмкостью) пластин. Электроёмкость любого проводника (или системы проводников) численно равна отношению заряда, сообщённого проводнику, к потенциалу, до которого зарядился проводник:
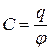. (19)
Из формулы (17) следует, что ёмкость плоского конденсатора в системе СИ
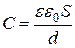, (20)
где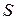 
— площадь пластины (обкладки) конденсатора, 
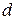— величина зазора между обкладками, 
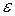— относительная диэлектрическая проницаемость вещества, заполняющего зазор.
Величина ёмкости плоского конденсатора, как следует, из формулы 20, определяется геометрией конденсатора (формой и размерами пластин и величиной зазора между ними), а также свойствами диэлектрика, находящегося между пластинами. Для получения больших ёмкостей применяют так называемые сложные конденсаторы, в которых пластины сделаны из алюминия, а диэлектриком являются листы провощенной бумаги.
Единицей измерения ёмкости в СИ является фарада (Ф)
.
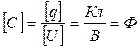На практике применяются более мелкие единицы: микрофарада (мкФ) и пикофарада (пФ)
.
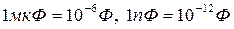Помимо ёмкости конденсатор характеризуется предельным напряжением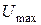 
. Подключение к пластинам конденсатора напряжения выше 
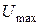может вызвать его пробой, в результате чего диэлектрик разрушится и конденсатор выйдет из строя.
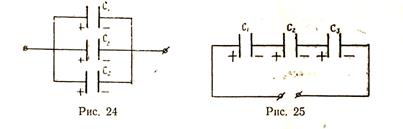
При включении в электрическую цепь нескольких конденсаторов применяют параллельное, последовательное и смешанное их соединения. При параллельном соединении (рис. 24) общая (эквивалентная) ёмкость равна сумме ёмкостей отдельных конденсаторов:
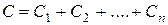. (21)
При последовательном соединении (рис. 25) конденсаторов обратная величина общей ёмкости равна сумме обратных величин ёмкостей отдельных конденсаторов:
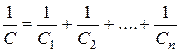. (22)
В настоящее время изготавливаются конденсаторы с самыми различными диэлектриками различной формы. Кроме плоской, конденсаторы могут иметь цилиндрическую или сферическую формы. Кроме того, конденсаторы изготавливаются постоянной, переменной и полупеременной ёмкости (триммеры). Ёмкость переменных и полупеременных конденсаторов изменяется путём поворота одних пластин по отношению к другим. При этом изменяется площадь пластин, находящаяся в электрическом поле. В конденсаторах переменной и полупеременной ёмкости применяются обычно газообразные и жидкие диэлектрики.
Конденсаторы широко применяются в электрорадиотехнических устройствах. Конденсаторы переменной ёмкости используются для настройки контуров радиосхем передатчиков и приёмников.
Существуют различные методы измерения ёмкости конденсатора. Одним из них является определение ёмкости конденсатора баллистическим методом.
Ёмкость конденсатора связана с зарядом соотношения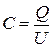 
. Напряжение на конденсаторе определяется по вольтметру, подключенному к источнику, заряжающему конденсатор. Таким образом, для определения ёмкости конденсатора нужно измерить заряд, находящийся на пластинках конденсатора. Заряд конденсатора можно измерить с помощью зеркального баллистического 
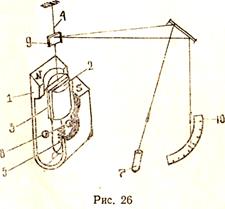гальванометра, работающего в баллистическом режиме.
Гальванометр — это прибор высокой чувствительности, который используется для измерения малых значений тока, напряжений и количества электричества. Наибольшее распространение получили гальванометры магнитоэлектрической системы.
Баллистический гальванометр представляет собой разновидность зеркального гальванометра (рис. 26). Измерительный механизм гальванометра состоит из подвешенной на вертикальной нити рамки 3, помещённой в поле постоянного магнита 1. К рамке прикреплён полый цилиндр 2 из мягкого железа, благодаря которому магнитное поле вблизи рамки делается радиально симметричным. Прямоугольная рамка 3 намотана из медной изолированной проволоки диаметром в несколько сотых миллиметра. По рамке пропускается измеряемый ток, который подводится через нить подвеса 4 из платиновой проволоки (диаметром в несколько микрон) и серебряный или золотой волосок 5 (толщиной в несколько микрон).
Рамка вместе с цилиндром может свободно поворачиваться в магнитном поле.
Прикрепленный к рамке цилиндр сильно увеличивает момент инерции и, следовательно, период колебания подвижной системы.
Если пропустить через рамку короткий импульс тока, то можно считать, что весь ток успевает пройти при неотклонённом положении. Рамка, однако, при этом получает толчок, в результате которого возникает её колебательное затухающее движение. Можно показать, что угол отброса рамки 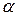пропорционален количеству электричества, протекающему через баллистический гальванометр, если длительность импульса тока меньше одной десятой периода колебания подвижной системы. При этом можно принять
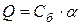, (13)
где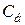 
— баллистическая постоянная гальванометра.
Величина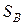 
, обратная 
,
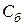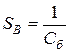(14)
называется баллистической чувствительностью гальванометра; она зависит от его конструкции и сопротивления внешней цепи гальванометра.
Из изложенного следует, что для получения достаточно точного измерения заряда конденсатора необходимо, чтобы гальванометр имел большой период колебаний (в десятки раз превышающий длительность импульса тока).
Гальванометр должен иметь настолько большой период колебаний, чтобы можно было успеть произвести отсчёт величины наибольшего отброса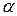 
. С этой целью в баллистическом гальванометре подвижную часть делают с относительно большим моментом инерции. Увеличение момента инерции достигается увеличением массы подвижной части гальванометра, например, за счёт применения двух или четырёх грузиков 6.
Угол поворота рамки измеряется с помощью светового указателя с двукратным отражением луча. От лампы 7, имеющей оптическую систему и диафрагму, луч после отражения от зеркала 9 подвижной части попадает на шкалу 10 и даёт изображение светового пятна. Поворот подвижной части вызовет перемещение по шкале светового пятна («зайчика»). Таким образом,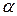 
представляет собой угол поворота подвижной части (при первом её отклонении), измеряемый в делениях шкалы 
.
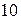Значение баллистической постоянной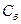 
можно определить, разряжая через баллистический гальванометр конденсатор известной ёмкости 
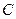, заряженный до разности потенциалов U.
Описание установки
Для определения ёмкости конденсатора баллистическим методом, используется схема, изображенная на рис. 27.
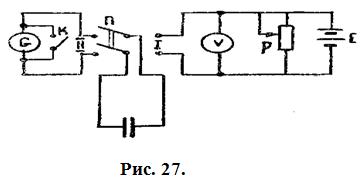На рисунке схемы G — баллистический гальванометр, С — исследуемый конденсатор. Когда переключатель П установлен в положение I, происходит зарядка конденсатора от батареи Е. Когда переключатель установлен в положение II, конденсатор разряжается через гальванометр G. Ключ К служит для резкого торможения подвижной части гальванометра, после прекращения импульса тока в рамке. Этот ключ замыкается только на короткое время в момент прохождения светового луча через среднее положение.
Порядок выполнения работы
Задание 1. Определение баллистической постоянной гальванометра
1. Включить в схему эталонный конденсатор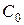 
, для чего присоединить его к клеммам переключателя П.
2. Пользуясь потенциометром Р, вольтметром и переключателем П, устанавливаемым в положение I, зарядить конденсатор до ЗВ.
3. Произвести разряд конденсатора на гальванометр, переключая ключ П из положения I в положение II.
4. Замер повторить пять раз при напряжениях: 2, 4, 5, 6, 7В. Результаты занести в табл. 1.
5. Найти баллистическую постоянную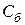 
по формуле:
.
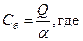
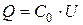Таблица 1
| № п/п |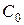
| U |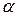 
| 
| 
| 
|
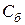
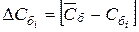
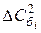
| 1 | ||||||
| · | ||||||
| · | ||||||
| · | ||||||
| 5 |
6.Вычислите доверительный интервал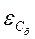 
по заданной доверительной вероятности 
:
.
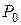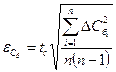7.Оценить границу абсолютной допустимой ошибки вольтметра и гальванометра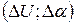 
.
8.Вычислить относительную приборную ошибку, допущенную при определении баллистической постоянной по формуле:
,
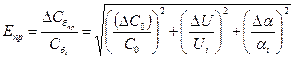где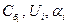 
берутся из табл. 1 и соответствуют случаю, когда 
, 
.
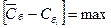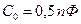9.Вычислить абсолютную приборную погрешность баллистической постоянной:
.
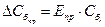10.Сравнить абсолютную приборную погрешность и доверительный интервал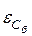 
. Если они одного порядка, то ошибка измерения вычисляется по формуле:
.
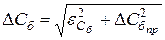Если они отличаются хотя бы на порядок, то берется наибольшая ошибка.
Задание 2. Определение ёмкости конденсатора
1.Включить в схему вместо эталонного конденсатора конденсатор неизвестной ёмкости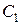 
. Измерения провести при 3-х напряжениях (3, 6 и 8 В).
2.То же самое проделать применительно ко второму конденсатору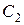 
неизвестной ёмкости.
3.Воспользовавшись результатами расчёта баллистической постоянной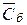 
из предыдущего эксперимента, вычислить ёмкости конденсаторов 
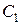и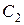 
по формуле 
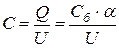для трёх напряжений. Определить среднее значение 
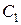и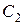 
.
4.Результаты эксперимента и расчёта занести в табл. 2.
Таблица 2
| Конденсаторы | Номер опыта |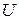 
| 
| 
|
| 
|
|
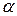
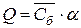
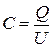
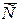
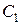
| 1 2 3 |
|
|
|
|
|
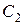
| 1 2 3 |
Задание 3. Определение ёмкости батареи из двух конденсаторов при параллельном и последовательном соединениях
1.Присоединить к клеммам переключателя П конденсаторы 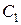и 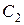сначала параллельно, а потом последовательно и произвести измерения. Если при параллельном соединении «зайчик» уходит за пределы шкалы, то надо уменьшить напряжение заряда конденсатора.
2.Результаты эксперимента по определению общей ёмкости батарей конденсаторов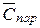 
и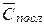 
занести в табл. 3.
3.Сравнить результаты опыта с результатами вычислений ёмкости батарей по формулам (21) и (22), при этом вместо 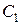и 
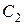подставить их средние значения из табл. 2. Результаты вычислений сравнить с результатами эксперимента.
Таблица 3
| Вид соединения в батарею | Номер опыта | U |
|
| Общая ёмкость батареи | |
из опыта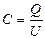 
| Из вычислений | |||||
| Параллельно | 1 2 3 |
|
|
|
|
|
| Последовательно | 1 2 3 | |||||
Контрольные вопросы
1. Что называется напряжённостью электрического поля? В чём она измеряется и каков физический смысл этой величины?
2. Что такое потенциал поля? В чём он измеряется и каков его физический смысл?
3. Нарисуйте силовые линии точечных положительного и отрицательного зарядов.
4. Что называется поверхностной плотностью зарядов?
5. Что такое электроёмкость проводника? В чём она измеряется?
6. Что такое конденсатор? Каково его устройство? Какие бывают виды конденсаторов? Запишите формулы для ёмкостей известных вам конденсаторов.
7. Какое устройство имеют конденсаторы переменной ёмкости и где они применяются?
8. Изобразите схемы параллельного, последовательного и смешанного соединений проводников.
9. Как изменится ёмкость батареи конденсаторов, если один из них выйдет из строя в случае, когда конденсаторы соединены:
а) параллельно?
б) последовательно?
ЛАБОРАТОРНАЯ РАБОТА № 11
Дата: 2018-12-21, просмотров: 289.
