| НАЧАЛО |
| _X1[1] := X[1, 1]; _X1[2] := X[1, 2]; _X2[1] := _X1[1] + 2 * Eps; _X2[2] := _X1[2] + 2 * Eps; alpha := 1; Sol := false; |
| A (((Abs(_X1[1] - _X2[1]) > Eps)or(Abs(_X1[2] - _X2[2])> Eps)) and (Sol = false)) |
| _X2[1] := _X1[1]; _X2[2] := _X1[2]; |
| (G1(_X1[1], _X1[2]) <= 0) and (G2(_X1[1]) <= 0) and (G3(_X1[2]) <= 0) |
| 2 |
| then |
| else |
| switcher = false |
| 2 |
| switcher = false |
| Sol := MyProstSluchOpt.GetSolution (_X1, Eps, 0); |
| Sol := MyOptGradMeth.GetSolution (_X1, Eps, alfa) |
| Sol := MyProstSluchOpt.GetSolution (_X1, Eps, alfa); |
| Sol := MyOptGradMeth.GetSolution (_X1, Eps, 0) |
| else |
| then |
| then |
| else |
| n := n + 1; |
| n := n + 1; |
| КОНЕЦ |
| switcher = false |
| then |
| else |
| alfa := alfa * 2 |
| alfa := alfa * 5; |
| 3 |
| Executing := Sol; |
| 3 |
Пример работы программы при начальной точке внутри ограничений:
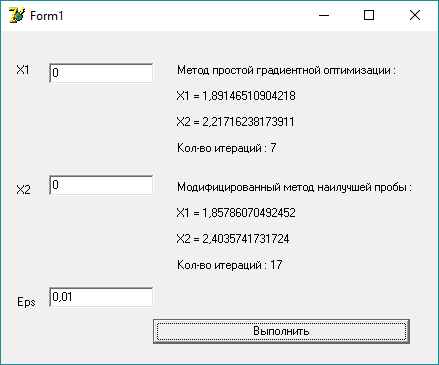
В данном примере выбрана начальная точка (0; 0), которая удовлетворяет всем ограничениям. Программа находит условный минимум целевой функции за 7 шагов методом простой градиентной оптимизации за 17 шагов модифицированным методом наилучшей пробы и сходится к значению (1.9; 2.3).
Пример работы программы при начальной точке вне ограничений:
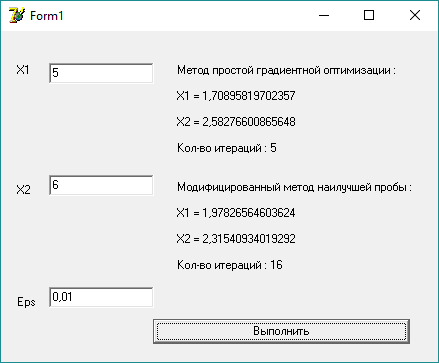
В данном примере начальная точка не удовлетворяет всем ограничениям, поэтому вначале программа приходит к точке (5; 6), что является безусловным минимумом целевой функции, но после этого текущая точка перестает удовлетворять всем ограничениям и на целевую функцию налагается штраф, что приводит к “сваливанию” точки к границе одного из ограничений. Программа приходит к условному минимуму функции (1.9; 2.3) за 5 шагов методом простой градиентной оптимизации и за 16 шагов модифицированным методом наилучшей пробы.
Выводы:
Во второй части курсовой работы я находила условный минимум целевой функции. Для этого я использовала метод сводящий задачу условного минимума к безусловной, а именно, метод штрафной функции (внешней точки). Данный метод позволяет находить условный минимум функции для любой начальной точки, а также очень прост в реализации на языке программирования.
Как подпрограмму для безусловной оптимизации я использовал 2 метода, рассмотренных в первой части – метод градиентной оптимизации и модифицированный метод наилучшей пробы. Программа с методом сопряженных градиентов находит условный минимум с лучшей точностью в сравнении с модифицированным методом наилучшей пробы.
Листинг основной подпрограммы:
function MSF.Executing(var X : TArg; Eps : real; var n : integer; switcher : boolean) : boolean;
Var
alfa : real;
Sol : boolean;
_X1, _X2 : TVector;
MyProsGrOpt : TProsGrOpt;
MyMetNaiProb : TMetNaiProb;
Begin
n := 0;
MyProsGrOpt := TProsGrOpt.Create;
MyMetNaiProb := TMetNaiProb.Create;
_X1[1] := X[1, 1]; _X1[2] := X[1, 2]; _X2[1] := _X1[1] + 2 * Eps; _X2[2] := _X1[2] + 2 * Eps;
alfa := 1;
Sol := false;
while (((Abs(_X1[1] - _X2[1]) > Eps)or(Abs(_X1[2] - _X2[2])> Eps)) and (Sol = false)) do
begin
_X2[1] := _X1[1]; _X2[2] := _X1[2];
if ((G1(_X1[1], _X1[2]) <= 0) and (G2(_X1[1], _X1[2]) <= 0) and (G3(_X1[2]) <= 0)) then
begin
if (switcher = false) then Sol := MyProsGrOpt.GetSolution(_X1, Eps, 0)
else Sol := MyMetNaiProb.GetSolution(_X1, Eps, 0);
n := n + 1;
end
else
begin
if (switcher = false) then Sol := MyProsGrOpt.GetSolution(_X1, Eps, alfa)
else Sol := MyMetNaiProb.GetSolution(_X1, Eps, alfa);
n := n + 1;
if (switcher = false) then alfa := alfa * 7
else alfa := alfa * 1.6;
end;
X[n, 1] := _X1[1]; X[n, 2] := _X1[2];
end;
Executing := Sol;
end;
function MSF.G1(X1, X2 : real) : real;
Begin
G1 := 2 * X1 + X2 - 6;
end;
function MSF.G2(X1, X2 : real) : real;
Begin
G2 := - 2 * X1 + X2 - 4;
end;
function MSF.G3(X2 : real) : real;
Begin
G3 := - X2 - 3;
end;
End.
Дата: 2018-12-21, просмотров: 320.