Постановка задачи
Рассматривается задача условной оптимизации (нелинейного программирования) с ограничивающими неравенствами:
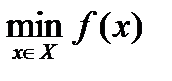
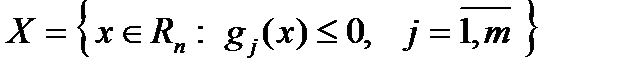
Моему варианту соответствует:
| f(x1, x2) | gi (x1, x2) ≤ 0, i = 1,m |
| (х1 – 5)2 + 2(х2 – 3)2 | 2х1 + х2 - 6 |
| -2х1 + х2 - 4 | |
| -х2 - 3 |
Данную задачу я буду решать двумя способами:
1) Сведением задачи условной оптимизации к задаче безусловной оптимизации;
2) Применяя метод прямой условной оптимизации, который непосредственно учитывает ограничения;
Метод штрафной функции
Методы «штрафных» функций характеризуются простотой реализации алгоритмов и широкими возможностями применения большинства методов безусловной оптимизации. Это достигается с помощью специальной процедуры сведения задач условной оптимизации к безусловной.
Введем в рассмотрение функцию s ( x , a ), именуемую в дальнейшем функцией «штрафа» («штрафной» функцией), со следующими свойствами.
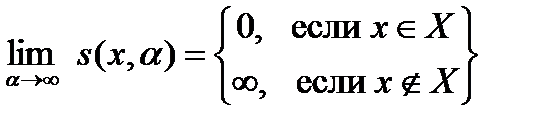(6.3)
В идеальном случае, при a ® ¥ «штрафная» функция будет иметь вид, представленный на рис. 6.1
Гипотеза:
Предполагается, что задача 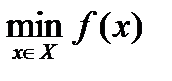, 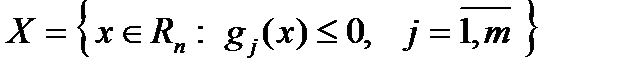эквивалентна задаче безусловной оптимизации следующего вида:
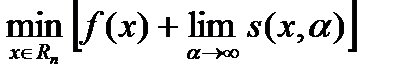, (6.4)
| X |
| f(x) |
| s(x,a), a®¥ |
| f(x) |
| x |
| s(x,a) |
| ¥ |
Рис.6.1
При наличии нескольких ограничений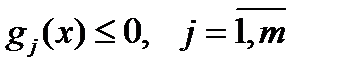 
, каждой из них будет соответствовать своя штрафная функция sj ( x , a ) 
.
Если ввести новую функцию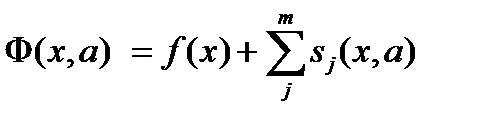 
, то решение задачи условной минимизации (6.1), (6.2) может быть приближенно получено с помощью итеративной процедуры безусловной оптимизации:
(6.5)
где последовательность коэффициентов a i строится по правилу:
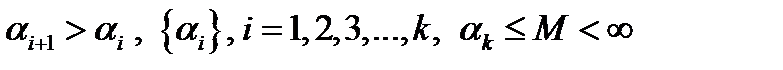(6.6)
При этом, с ростом a i , соответствующая последовательность решений задач безусловной оптимизации будет приближаться к решению задачи условной оптимизации (6.1), (6.2) :
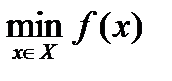Þ (6.7)
Широко используются два основных подхода к построению функций «штрафа». Для решения своей задачи я буду использовать метод внешней точки, т.к. начальная точка может не удовлетворять всех ограничениям и при этом метод внутренней точки будет неприменим.
Метод внешней точки (Метод «штрафных» функций)
Идея метода
В качестве «штрафных» функций используются зависимости, которые внутри области Х близки или равны нулю, а при удалении (во вне) от границы допустимой области вариаций параметров (аргументов) – неограниченно возрастают.
На рис. 6.3 представлены тенденции изменений итеративных решений с ростом коэффициентов a i .
| s(x,a1) |
| s(x,a2) |
| F(x,a1) |
| F(x,a2) |
| f(x) |
| exp |
| xmin x*(ai) |
| x |
| f(x) |
| a2>a1 |
| X |
Рис.6.3
Штрафная функция будет иметь вид:
sj(2)(x , a) = a [ max (0, gj(x))]2
В качестве подпрограммы для безусловной оптимизации будет использоваться метод сопряженных градиентов из I Части курсовой работы.
Блок-схема метода штрафной функции (внешней точки)
Дата: 2018-12-21, просмотров: 227.
