Деление окружности на равные части и построение правильных вписанных многоугольников можно выполнить как циркулем, так и с помощью угольников и рейсшины.
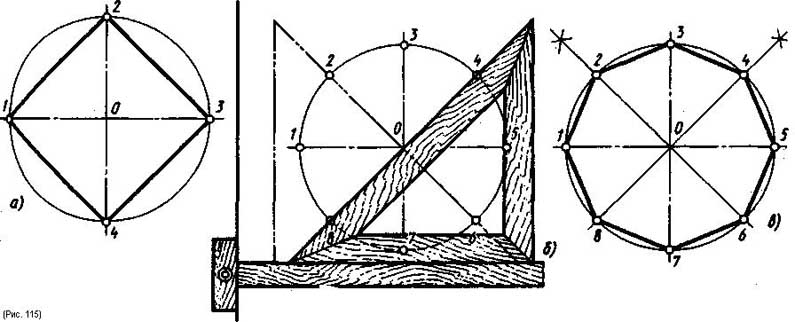
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
Деление окружности на восемь равных частей и построение п р а в ильного вписанного восьмиугольника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 10° и рейсшины (рис. 115, б), вместе с центровыми линиями разделят окружность на восемь равных частей. Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из :чек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом Делаются засечки до взаимного пересечения, м же радиусом делают две засечки из точек и 5 (рис. 115, в). Через точки пересечения сечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6,8.
Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 115, в).
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.
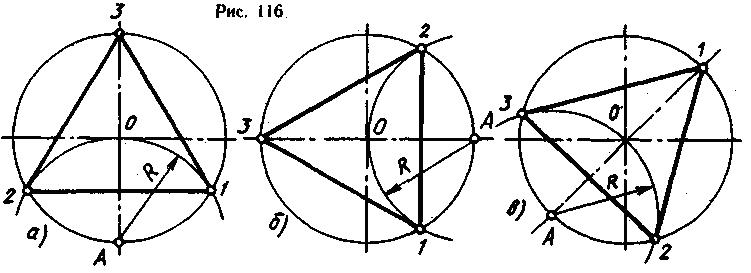
При делении окружности циркулем на три равные части из любой точки окружности, например из точки А пересечения центровых линий с окружностью (рис. 116, ей б), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку А. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R, равным радиусу данной окружности, получают точки 2 и 3.
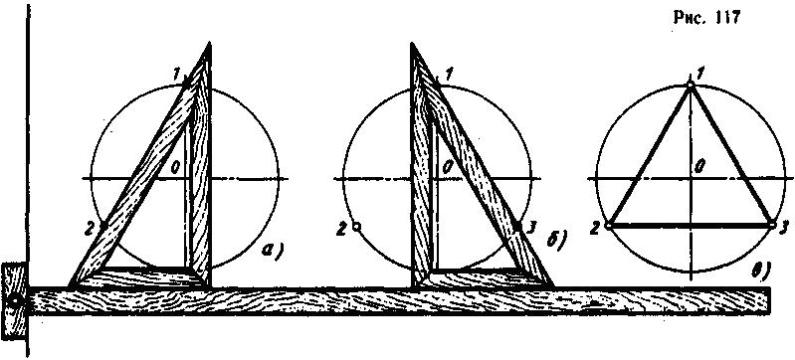
При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
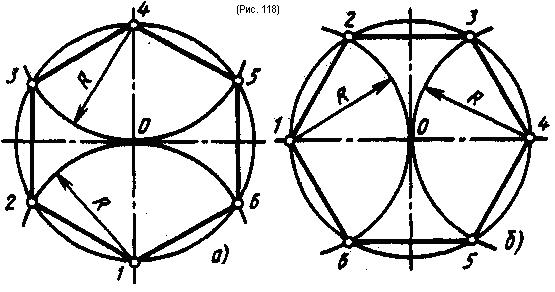
При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120.
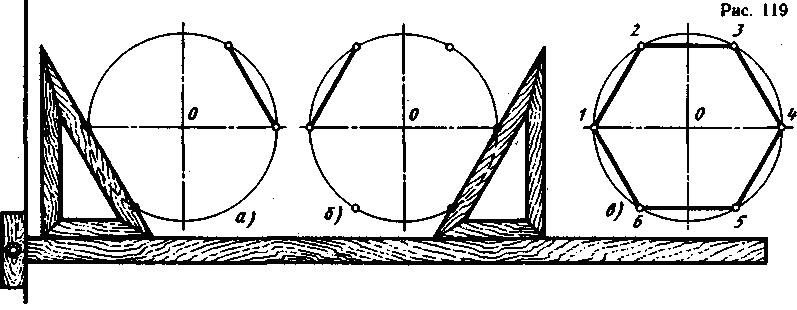
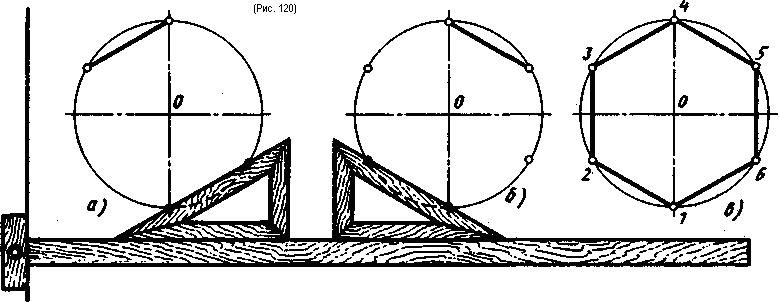
Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.
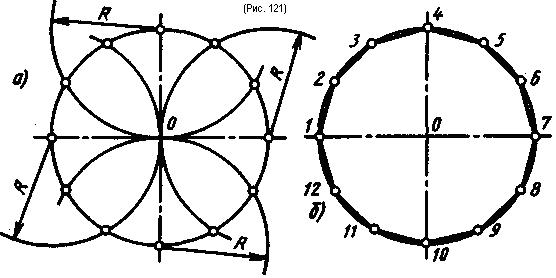
При построении двенадцатиугольника с помощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.
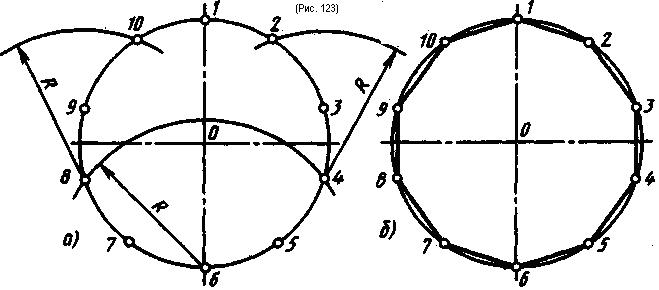
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 122.
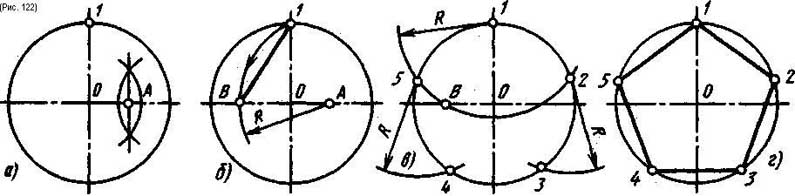
Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности. Делая засечки на окружности (рис. 122, в) радиус сом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник (рис. 123, б).
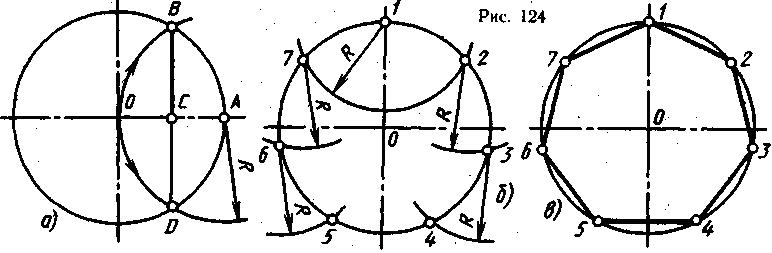
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного многоугольника и четырнадцатиугольника показано на рис. 124 и 125. Из любой точки окружности; например точки - А, радиусом заданной окружности проводят (рис. 124, а) до пересечения с окружностью в точках В и D. Соединим точки В прямой. Половина полученного отрезка (в ном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС, ставят засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильно вписанный семиугольник (рис. 124, в). Деление окружности на четырнадцать равных частей выполняется делением окружности семь равных частей два раза от двух точек (125, а).
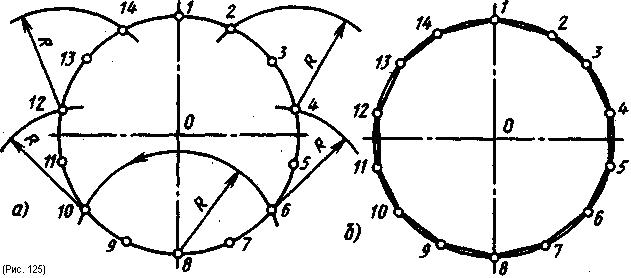
Сначала окружность делится на семь равных частей от точки 1; затем то же построение отклоняется от точки 8. Построенные точки отклоняют последовательно прямыми линиями получают правильный вписанный четырнадцатиугольник (рис. 125, б).
СОПРЯЖЕНИЯ
Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.
На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхности. На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности - дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
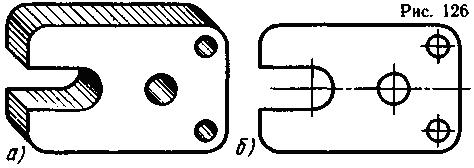
Плавный переход одной цилиндрической поверхности в другую может являться цилиндрической поверхностью (рис. 127, а). На чертеже эти цилиндрические поверхности изображены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окружности в другую осуществляется дугой окружности заданного радиуса.
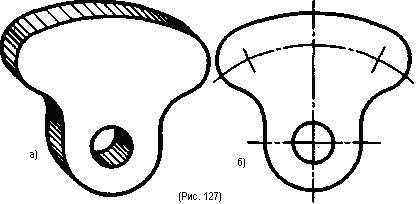
На рис. 126, а и 127, а рассмотрены простейшие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображаются различными сочетаниями прямых, окружностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет одно - плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е, найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Задачи на сопряжения условно можно разделить на три группы.
Первая группа задач включает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.
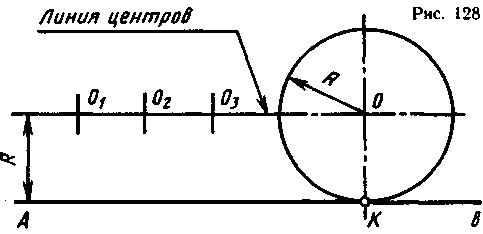
Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.
Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. .128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O1, O2 и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окружность. Задача аналогична предыдущей, но дополнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.
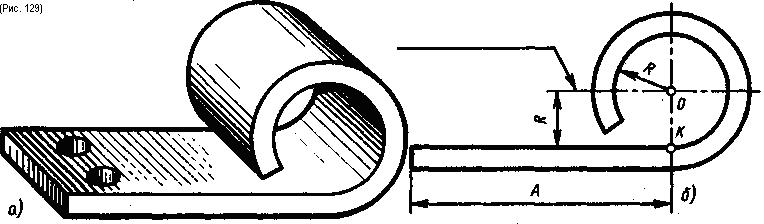
Отложив размер Л, находят точку касания (точку К), затем из точки К восставляют перпендикуляр, на котором откладывают радиус R заданной окружности, и находят центр окружности (точку О). При обводке сначала от точки касания проводится дуга заданного радиуса, а потом - прямая.
Из сказанного следует:
1. центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;
2. точка касания лежит на перпендикуляре, проведенном из центра окружности к заданной прямой.
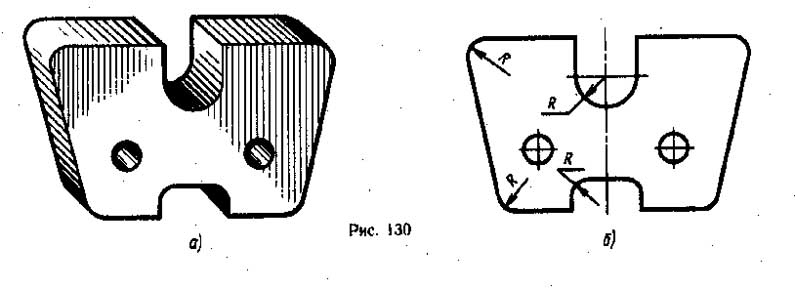
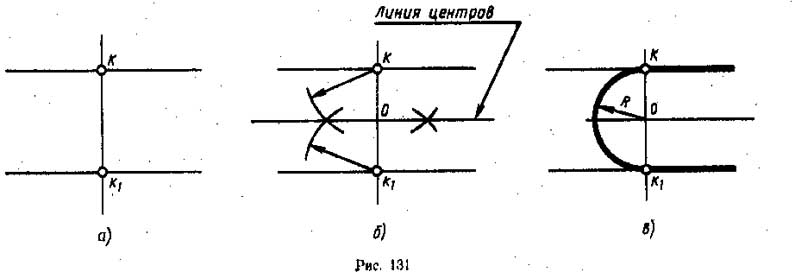
Сопряжение двух прямых. На плоскости две прямые могут располагаться параллельно или под углом друг к другу. На рис. 130 приведены примеры различных сопряжений двух прямых. Чтобы построить сопряжение двух прямых, необходимо провести окружность, касательную к этим двум прямым.
Сопряжение двух параллельных прямых. Чтобы построить сопряжение двух параллельных прямых, необходимо провести дугу окружности, касательной к этим прямым (рис. 131). Радиус этой окружности будет равен половине расстояния между заданными прямыми. Так как точка касания не задана, подобных окружностей можно провести множество. Центры их будут находиться на прямой, проведенной параллельно заданным прямым на расстоянии, равном половине расстояния между ними. Эта прямая будет линией центров. Точки касания (К и K1) лежат на перпендикуляре, опущенном из центра касательной окружности на заданные прямые (рис. 131, а). Так как центр касательной окружности не задан, перпендикуляр проводится произвольно. Отрезок КК1 делят пополам (рис. 131, б), проводят через точки пересечения засечек прямую линию параллельно заданным прямым, на которой будут располагаться центры окружностей, касательных к заданным параллельным прямым, т. е. эта линия будет линией центров. Поставив ножку циркуля в точку О, проводят дугу сопряжения (рис. 131, в) от точки К до точки К1.
Сопряжение двух непараллельных прямых. Две непараллельные прямые располагаются друг к другу под углом, который может быть прямым, тупым или острым. При выполнении чертежей деталей часто такие углы необходимо скруглить дугой заданного радиуса (см. рис. 130). Скругление углов на чертеже есть не что иное, как сопряжение двух непараллельных прямых дугой окружности заданного радиуса. Для выполнения сопряжения необходимо найти центр дуги сопряжения и точки сопряжения. Известно, что если в сопряжении участвует прямая линия, то центр дуги сопряжения находится на линии центров, которая проводится параллельно заданной прямой на расстоянии, равном радиусу R дуги сопряжения. Поскольку угол образован двумя прямыми, то проводят две линии центров параллельно каждой прямой на расстоянии, равном радиусу R дуги сопряжения (рис. 132). Точка их пересечения будет центром дуги сопряжения.
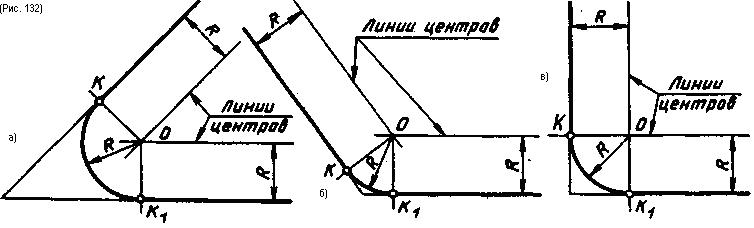
Для нахождения точек сопряжения из точки О опускают перпендикуляры на заданные прямые и получают точки сопряжения К и К1 (рис. 132). Зная точки и центр сопряжения, из точки О радиусом R проводят дугу сопряжения. При обводке чертежа следует сначала обвести дугу, а затем касательные прямые.
При построении сопряжения прямого угла упрощается проведение линии центров, так как стороны угла взаимно перпендикулярны. От вершины угла откладывают отрезки, равные радиусу R дуги сопряжения, и через полученные точки К и К1, которые будут точками касания, проводят две линии центров, параллельные сторонам угла. Они будут являться одновременно и линиями центров, и перпендикулярами, определяющими точки сопряжения К и К1 (рис. 132, в).
Построение прямых, касательных к окружностям, зависит от условия задачи. Может быть задана окружность с точкой касания, или окружность и точка, из которой следует провести касательную прямую, или две окружности, к которым нужно провести касательную прямую. Подход к решению этих за дач будет различным, но во всех случаях существует одно правило: точка касания должна лежать на перпендикуляре, проведенном из центра окружности к прямой.
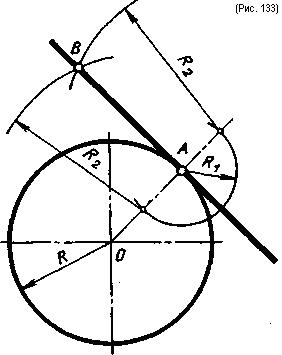
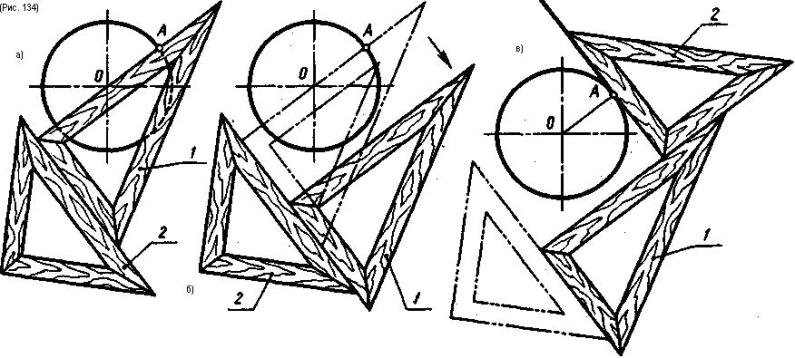
Проведение прямой, касательной к окружности через точку, лежащую на окружности, показано на рис. 133. Так как точка касания лежит на перпендикуляре, проведенном из центра окружности к прямой, то касательную прямую следует проводить через заданную точку А перпендикулярно радиусу, соединяющему точку А с центром окружности О (рис. 133). Это построение аналогично построению перпендикуляра к прямой через заданную точку, которое можно выполнить с помощью двух угольников (рис. 134). Сначала угольник 1 (рис. 134, а) кладется так, чтобы одна его сторона совпала с точками О и А, затем к угольнику 1 прикладывается угольник 2, который будет направляющим, по которому сдвигается угольник 1 (рис. 134, б). В новом положении угольник 1 становится направляющим, а угольник 2 устанавливается на угольник 1 так, чтобы одна сторона его прямого угла прошла через точку А (рис. 134, в). Через точку А по угольнику 2 проводят прямую, касательную к окружности.
Проведение прямой, касательной к окружности через точку, не лежащую на этой окружности. Даны окружность радиусом R и точка А, не лежащая на окружности (рис. 135, а), требуется провести из точки А прямую, касательную к данной окружности в верхней ее части. Для этого необходимо найти точку касания. Точка касания лежит на перпендикуляре, проведенном из центра окружности к касательной прямой. Следовательно, касательная и перпендикуляр образуют прямой угол. Зная, что всякий угол, вписанный в окружность и опирающийся на ее диаметр, является прямым, соединив точки А и О, принимают отрезок АО за диаметр описанной окружности. В пересечении описанной окружности и окружности радиуса R будет находиться вершина прямого угла (точка К). Отрезок АО делят пополам, получают точку 01 (рис. 135, б). Из центра 01 радиусом, равным отрезку АО1, проводят окружность, получают точки К и К1 в пересечении с окружностью радиуса R (рис. 135, в) Так как нужно провести только одну касательную к верхней части окружности, выбирают нужную точку касания. Этой точкой будет точка К. Точку К соединяют с точками А и О, получают прямой угол, который опирается на диаметр АО описанной окружности радиусом R1. Точка К - вершина этого угла (рис. 135 г), отрезки ОК и АК - стороны прямого угла, следовательно, точка К будет искомой точкой касания, а прямая АК - искомой карательной.
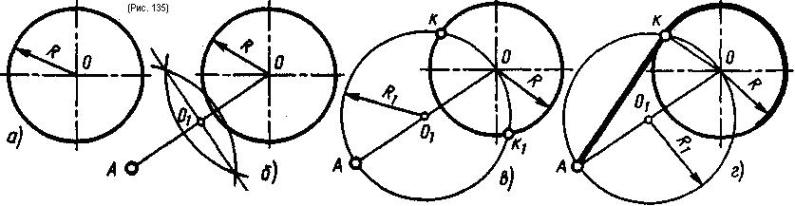
Проведение прямой, касательной к двум окружностям. Даны две окружности радиусами R и R1, требуется построить касательную к ним. Возможны два случая касания: внешнее и внутреннее.
При внешнем касании касательная прямая находится с одной стороны от окружностей и не пересекает отрезок, соединяющий Центры данных окружностей (рис. 136, а). При внутреннем касании касательная прямая находится с разных сторон от окружностей и пересекает отрезок, соединяющий центры окружностей (рис. 136, б).
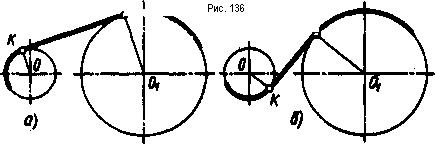
В н е ш н е е к а с а н и е. Прежде всего необходимо найти точки касания. Известно, что они должны лежать на перпендикулярах, проведенных из центров окружностей (О и 01') к касательной. Рассмотрим рис. 137, г, где задача уже решена. Найденные точки касания К1 и Кз лежат на перпендикулярах O1К1 и О1Са. Если перемещать касательную К1К2 параллельно самой себе в направлении центров заданных окружностей, то точки К1 и К2 будут скользить по перпендикулярам O1К1 и ОК1. В конце концов точка Кз совпадет с центром О (окружности меньшего радиуса, а точка К1 - с точкой К). Так как касательная К1Кз перемещалась параллельно самой себе, то отрезки КзО и К1К равны, и отрезок К3О равен радиусу R. Через точку К из центра 01 проводим вспомогательную окружность радиусом R2 = R1-R. Далее построение будет как в предыдущей задаче - проведение прямой, касательной к окружности,, из заданной точки, не лежащей на этой окружности.
На рис. 137 показано поэтапное построение касательной к двум окружностям. Сначала строят касательную ОК из центра О к окружности радиуса R2 (рис. 137, а, б, в). Касательную ОК перемещают параллельно самой себе. Точки касательной при этом будут перемещаться по перпендикулярам к ней. Перпендикуляр 01К, по которому перемещается точка К, продолжают до пересечения с заданной окружностью радиуса R1, получают точку К1. Из точки О перпендикулярно ОК или параллельно 01К1 проводят прямую. Она будет тем перпендикуляром, по которому перемещается второй конец касательной ОК. В пересечении этого перпендикуляра с окружностью радиуса R получают вторую точку касания - Кз. Соединив точки К1 и К3, получают внешнюю касательную к двум заданным окружностям (рис. 137, г).
В н у т р е н н е е к а с а н и е. Построение внутренней касательной к двум заданным окружностям выполняют аналогично построению внешней касательной, только вспомогательную окружность радиуса R" проводят из центра 01 суммой радиусов R3 = R1 + R (рис. 138). Центры О и 01 соединяют прямой и отрезок 001 делят пополам в точке О3, из точки Оз проводят окружность радиуса R3. получают точку К. Точку К соединяют с центрами О и 01. Отрезок 01К пересекает окружность радиуса R1 в точке К1. Из центра О параллельно КО1 проводят прямую до пересечения ее с окружностью радиуса R в точке К3. Точки К1 и Кз будут точками касания, соединив которые получают внутреннюю касательную к двум заданным окружностям (рис. 138, б).
Вторая группа задач на сопряжения включает в себя задачи, в которых участвуют только окружности и дуги. Плавный переход одной окружности в другую может происходить или непосредственным касанием, или через третий элемент - дугу окружности.
К а с а н и е двух окружностей может быть внешним (рис. 139, а) или внутренним (рис. 140, а).
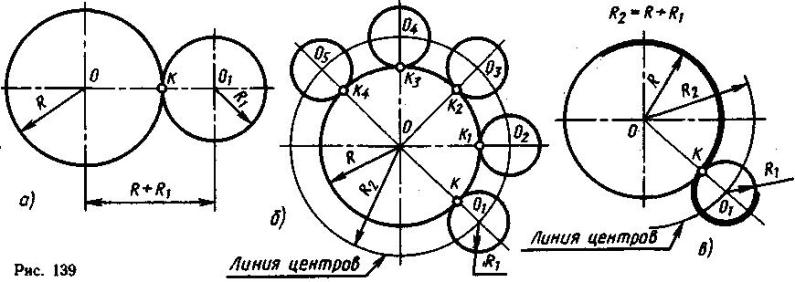
В н е ш н е е к а с а н и е. При внешнем касании двух окружностей расстояние между центрами этих окружностей будет равно сумме их радиусов (рис. 139).
Например, требуется построить плавный переход от окружности радиуса R к окружности радиуса R1 с внешней стороны, точка касания не задана. К окружности радиуса R можно построить множество касательных окружностей радиуса R1 с внешним касанием (рис. 139, б). Их центры (01, 02 и т. д.) будут находиться от центра О на одинаковом расстоянии, т. е. на окружности радиуса R2=R+R1 проведенной из центра О заданной окружности. Точки касания К, К1 и т. д. лежат на прямых, соединяющих центры сопрягающихся окружностей (рис. 139, б).
На рис. 139, в показано построение внешнего касания двух окружностей с произвольно выбранной точкой касания К.
В н у т р е н н е е к а с а н и е. При внутреннем касании двух окружностей одна из касательных окружностей находится внутри другой окружности, и расстояние между центрами этих окружностей будет равно разности их радиусов (рис. 140).
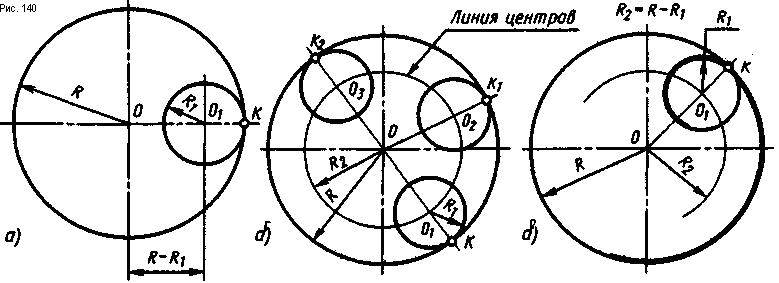
Например, требуется построить плавный переход от окружности радиуса R к окружности радиуса R1 с внутренней стороны, точка касания не задана. К окружности радиуса R можно построить множество касательных окружностей радиуса R1 с внутренней стороны (рис. 140, б). Их центры (01, О2 и т. д.) будут находиться на одинаковом расстоянии от центра О, т. е. на окружности радиуса R2 = R - R1, проведенной из центра О (рис. 140, б). Точки касания К, К1, К2 и т. д. лежат на прямых, проходящих через центры сопрягающихся окружностей (рис. 140, б). Так как точка касания не задана, на рис. 140, в показано построение внутреннего сопряжения двух окружностей с произвольно выбранной точкой касания.
Из рассмотренного выше следует, что если в сопряжении участвуют только окружности, то центр дуги сопряжения лежит на окружности, проведенной из центра заданной окружности радиусом, равным сумме или разности радиусов заданных окружностей, в зависимости от внешнего или внутреннего касания, точка касания лежит на прямой, соединяющей центры сопрягающихся окружностей. Для нахождения точки касания достаточно при внешнем касании только соединить центры (рис. 140, в), а ври внутреннем касании - соединить и продлить эту прямую. Сопряжение двух окружностей дугой заданного радиуса может быть внешним, внутренним и смешанным.
Внешнее сопряжение двух заданных окружностей дугой заданного радиуса. Если обе сопрягаемые окружности располагаются снаружи сопрягающей дуги, то центр этой дуги будет находиться от заданных окружностей на расстоянии, равном сумме радиусов (дуги и соответствующей окружности). Даны две окружности радиусов R и R1 (рис. 141, а), требуется построить внешнее сопряжение дугой радиуса R2. Известно, что для окружности радиуса R центр дуги сопряжения находится на линии центров, проведенной суммой радиусов R + R2 из центра О. Для окружности радиуса R1 центр дуги сопряжения лежит на линии центров, проведенной радиусом R4 = R1 + R2 из центра 01. Эти окружности (линии центров) проводят не полностью, а только до взаимного пересечения в точке О2 (рис. 141, а),. Точка О2 будет центром дуги сопряжения, так как она одновременно принадлежит двум линиям центров. Точка сопряжения лежит на прямой, соединяющей центр дуги сопряжения с центром заданной окружности, поэтому, соединяя точку О2 с точками О и 01 (рис. 141, б), в пересечении с заданными окружностями получают точки сопряжения К и К1. Из точки О2 радиусом R2 от точки К до точки К1 проводится дуга сопряжения. Затем от точек К и K1 обводят дуги радиусами R и R1 из центров О и 01 (рис. 141, б).
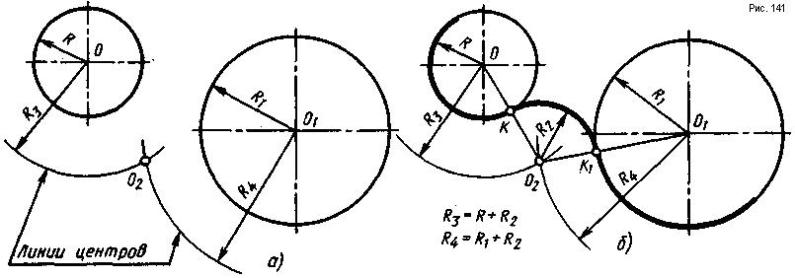
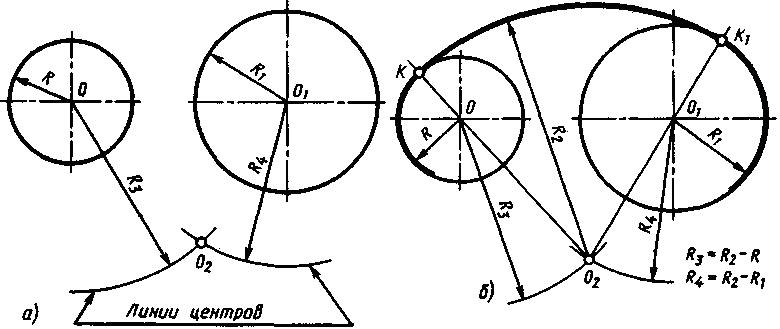
Внутреннее сопряжение двух окружностей дугой заданного радиуса. Сопрягаемые окружности располагаются внутри сопрягающей дуги, и центр сопрягающей дуги будет находиться от центров заданных окружностей на расстоянии, равном разности радиусов (дуги и соответствующей окружности).
Даны две окружности с радиусами R и R1 (рис. 142, а), требуется построить внутреннее сопряжение дугой радиуса R2 в верхней части. Известно, что для окружности радиуса R центр дуги сопряжения находится на линии центров, проведенной радиусом R3 = R2 - R из центра О заданной окружности. Для окружности радиуса R1 центр дуги сопряжения находится на линии центров, проведенной радиусом R4 = R2 - R1 из центра 01 заданной окружности. В нижней части чертежа из центров О и 01 радиусами Rз и R4 проводят дуги до взаимного пересечения в точке О2, которая будет центром дуги сопряжения, так как является общей точкой для двух линий центров (рис. 142, а). Находят точки сопряжения. Для этого точку О2 (центр дуги сопряжения) соединяют с точками О и 01 прямыми линиями, которые продлевают до пересечения с заданными окружностями в точках К и К1, которые будут точками сопряжения (рис. 142, б).
Смешанное сопряжение двух окружностей дугой заданного радиуса. В этом случае дуга сопряжения с одной окружностью имеет внешнее касание, а с другой - внутреннее.
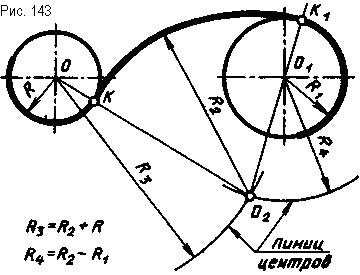
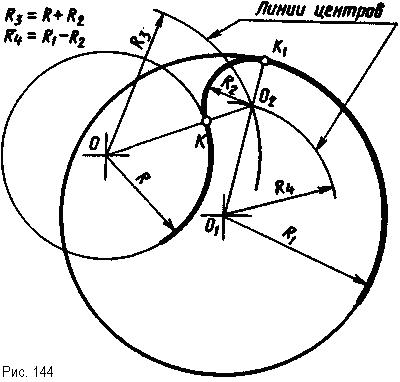
Даны две окружности с радиусами R и R1 (рис. 143), требуется построить сопряжение дугой радиуса R2 так, чтобы с окружностью радиуса R было внешнее касание, а с окружностью радиуса R1 - внутреннее. При внешнем касании линия центров - это окружность с радиусом, равным сумме радиусов заданной окружности и дуги сопряжения (R +R2), а при внутреннем - с радиусом, равным разности этих радиусов (R2 - R1). Поэтому из центра О проводят дугу (линию центров) радиусом R3, равным R + R2 (рис. 143), а из центра 01 - линию центров радиусом R4, равным R2 - R1 (рис. 143). В пересечении линий центров получают точку О2 (центр дуги сопряжения). Для нахождения точек сопряжения центр дуги сопряжения О2 соединяют с центрами О и 01 прямыми. Прямую О2О1 продолжают. В пересечении этих прямых с заданными окружностями получают точки сопряжения К и К1. Из точки О2 дугой радиуса R2 от точки К до точки К1 проводят дугу сопряжения (рис. 143).
Если две сопрягающиеся окружности имеют близко расположенные центры, то одна окружность может находиться внутри другой или они будут пересекаться друг с другом (рис. 144). Чтобы построить сопряжение, необходимо найти центр и точки сопряжения. Для этого радиусом Rз = R + R2 проводят дугу из центра О, а радиусом R4 = R1 - R2 - дугу линии центров из центра 01. В пересечении получают точку О2 - центр дуги сопряжения. Соединив точку О2 с точками О и 01 прямыми, получают точки сопряжения К и К1. Из центра О2 радиусом R2 проводят дугу сопряжения (рис. 144) от точки К до точки К1.
Третья группа задач включает в себя задачи на сопряжения прямой и дуги окружности дугой заданного радиуса.
Сопряжение прямой и дуги окружности дугой заданного радиуса. Выполняя такое построение, решают как бы две задачи: проведение касательной дуги к прямой и касательной дуги к окружности. Касание в этом случае может быть как внешним, так и внутренним.
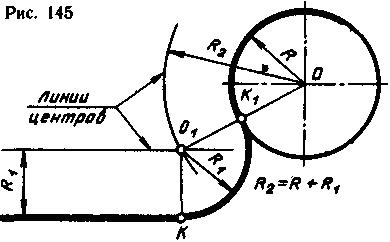
Внешнее касание. Заданы прямая и дуга окружности радиуса R, требуется построить сопряжение дугой радиуса R1. Так как сопрягается прямая линия, то центр дуги сопряжения находится на прямой, проведенной параллельно заданной прямой на расстоянии, равном радиусу сопряжения R1 (рис. 145). А центр дуги сопряжения при внешнем касании двух окружностей находится на окружности радиуса R2, равного сумме радиусов R и R1. В пересечении прямой и окружности (линий центров) получают точку 01, которая является центром дуги сопряжения. Затем находят точки сопряжения. Одна точка сопряжения - это точка пересечения заданной прямой с перпендикуляром, опущенным из центра дуги сопряжения 0 на эту прямую (точка К). Вторая точка сопряжения находится на пересечении заданной окружности и прямой, соединяющей центр дуги сопряжения с центром этой окружности (точка К1). Из точки 01 радиусом R1 проводят дугу сопряжения от точки К до точки К1.
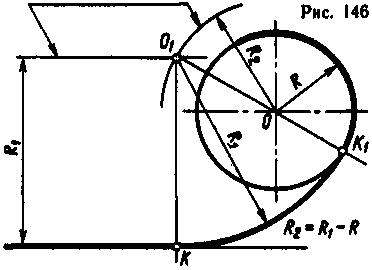
Внутреннее касание строится аналогично внешнему, только радиус R2 равен разности R1 -R (рис. 146).
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ СОПРЯЖЕНИЙ НА ЧЕРТЕЖАХ
Приступая к выполнению чертежа, проводят анализ графического изображения детали, т. е. определяют виды используемых сопряжений и способы их построения. При выполнении чертежа очень важна последовательность построений. Поэтому перед началом работы изображение мысленно разбивают на элементы и определяют последовательность их выполнения. Сначала вычерчивают элементы, которые будут сопрягаться, а затем строят сопряжения. При вычерчивании сопряжений необходимо точное построение точек сопряжения и центров дуг сопряжения.
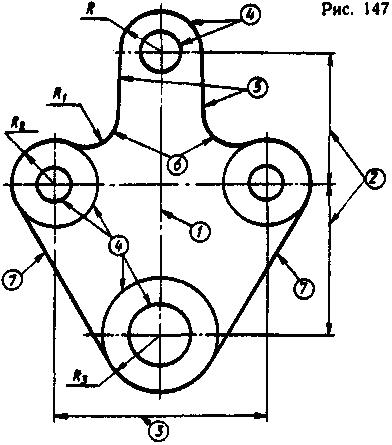
Рассмотрим изложенное выше на примере чертежа подвески, изображенного на рис. 147. По цифрам в кружках можно проследить последовательность выполнения элементов чертежа.
Начинают построение изображения с проведения оси симметрии (1), затем откладывают расстояние между центрами отверстий (2 и 3) и проводят центровые линии. Дальнейшую последовательность построении проследите по цифрам. Обводку чертежа начинают с проведения окружностей и дуг от точек сопряжения (касания).
УКЛОН И КОНУСНОСТЬ
Поверхности деталей часто представляют собой плоскости, расположенные наклонно друг к другу. Например, в литых и штампованных деталях, в изделиях проката (рельсы, балки, швеллеры). На чертежах подобные плоскости изображаются прямыми линиями.
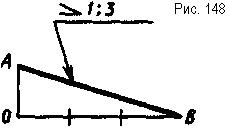
Уклон - это величина, которая характеризует наклон одной прямой относительно другой. На чертеже уклон выражается отношением двух чисел или в процентах. Обозначается уклон знаком >, размеры которого показаны на рис. 50, п. 18, согласно ГОСТ 2.304-81. Знак ставится перед числовым значением уклона над полкой линии выноски (рис. 148). Линия выноски заканчивается стрелкой, упирающейся в линию уклона. Острый угол знака должен быть направлен в ту же сторону, что и острый угол уклона.
Рассмотрим построение уклона, заданного отношением 1:3, относительно вертикального и горизонтального направлений (рис. 148, а и б). Сначала строят прямой угол АОВ. При горизонтальном направлении уклона (рис. 148)
а) откладывают отрезок произвольной величины по вертикальной стороне угла, получают точку А,, а при вертикальном направлении уклона (рис. 148, б) - по горизонтальной стороне угла. По второй стороне угла откладывают три таких отрезка, получают точку В. Соединив точки А и В прямыми, получают прямоугольный треугольник, гипотенуза которого будет располагаться под заданным уклоном.
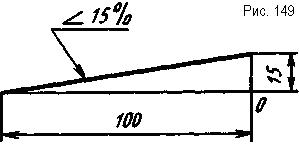
На рис. 149 уклон задан в процентах (15%). В этом случае строят прямой угол с вершиной О. На одной стороне угла (в данном случае горизонтальной) от точки О откладывают величину, принятую за 100%, например 100 мм, а на второй - от той же точки О откладывают величину, равную процентам заданного уклона, в данном случае 15 мм. Полученные точки соединяют прямой, которая будет располагаться с заданным уклоном.
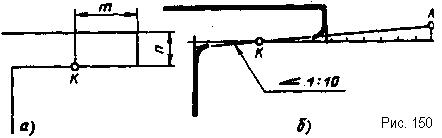
Если на чертеже требуется построить уклон 1:10 через заданную точку К, построение начинают от заданной точки, положение которой на чертеже .определяют размеры т и п (рис. 150, а). Для построения уклона от точки К вправо продлевают прямую линию, на которой от точки К откладывают десять одинаковых отрезков произвольной величины .(рис. 150, б). Из конца последнего отрезка проводят перпендикуляр, на котором откладывают величину одного такого отрезка, получают точку А. Через точки А и К проводят прямую с заданным уклоном.
Провести прямую с заданным уклоном через заданную точку можно, построив на свободном месте чертежа заданный уклон, потом с помощью двух угольников, параллельно построенному уклону, провести через заданную точку прямую.
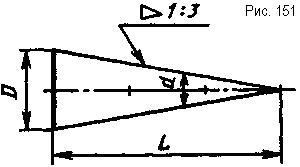
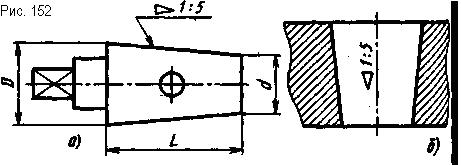
К о н у с н о с т ь - это отношение разноти диаметров двух поперечных сечений конуса к расстоянию между ними. Конусность обозначают буквой С, диаметр большего сечения - D, диаметр меньшего сечения - d, высоту - L. Конусность определяют по формуле С = (D - d)/L. Следовательно, для полного кругового конуса конусность определяется по формуле С = D/L (рис. 151). Конусность, так же как уклон, может быть задана на чертеже в процентах (20%) или отношением двух чисел (1:5). Чаще конусность задается в виде отношения двух чисел и обозначается знаком ◄, размеры которого определяет ГОСТ 2.304-81 (см. рис. 50, п. 19). Вершина знака должна быть, направлена в сторону вершины конуса. Знак наносят над полкой линии-выноски (рис. 152, а) или над осевой линией (рис. 152, б).
Если конус рассечь плоскостью на две части, то конусности этих частей будут одинаковыми (рис. 153, а и б), Несколько конусов с параллельными образующими будут иметь одинаковую конусность (рис. 153, в).
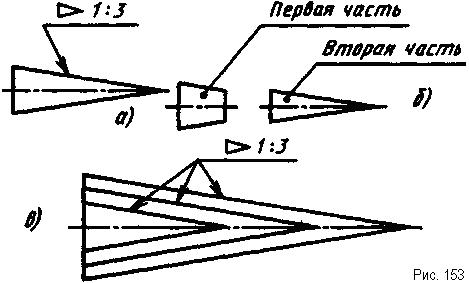
На рис. 154 приведено построение чертежа заготовки пробки с конусностью 1:5, диаметром Ø30 большего основания и расстоянием между основаниями 50 мм. Сначала строят элементы без конусности (рис. 154, а). Зная, что конусность - для полного конуса - это отношение диаметра основания к высоте, от оси конуса в обе стороны по диаметру 030 симметрично относительно оси откладывают отрезок произвольной длины, который будет основанием вспомогательного конуса. По оси конуса от основания вспомогательного конуса откладывают пять таких отрезков. Соединив, полученную точку с концами основания вспомогательного конуса, получают конус с конусностью 1:5 (рис. 154, а). Через концы диаметра 030 проводят прямые параллельно образующим вспомогательного конуса, до пересечения с вертикальной прямой, ограничивающей длину пробки, и получают меньшее основание усеченного конуса (рис. 154, б), размер которого не задан.
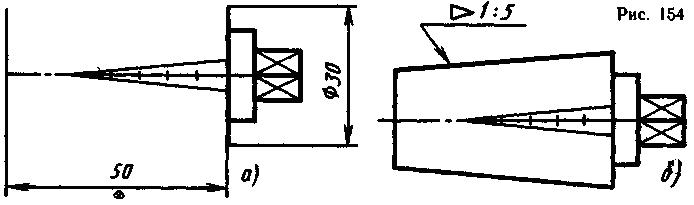
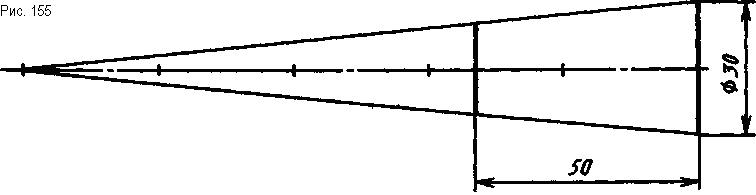
Если конусность небольшая, то заданный диаметр откладывают по осевой линии от основания в направлении высоты конуса столько раз, сколько указано в отношении. Построив тонкими линиями конус, отсекают часть заданной длины (рис. 155).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как провести несколько параллельных прямых, пользуясь угольником?
2. Как провести перпендикуляр к прямой с помощью циркуля и линейки?
3. Как определить центр дуги окружности, если он не задан?
4. Как разделить угол 90° на три равные части с помощью циркуля?
5. Как построить угол 75° с помощью угольников?
6. Как разделить окружность на три и шесть равных частей циркулем?
7. Что такое сопряжение?
8. Как определить точку касания при построении окружности, касательной к прямой?
9. Что представляет собой линия центров при. сопряжении двух окружностей (дуг)?
10. Какова последовательность выполнения чертежа детали, в очертании которой имеются сопряжения?
11. На каком расстоянии от центров заданных окружностей будет находиться центр касательной дуги при построении сопряжения двух окружностей дугой заданного радиуса при внешнем касании?
К р и в ы е л и н и и встречаются в очертаниях отдельных элементов деталей машин и механизмов, а также в очертаниях конструкций различных строительных сооружений. Если все точки кривой линии лежат в одной плоскости, такие кривые называют плоскими кривыми. Если точки кривой не лежат в одной плоскости, такие кривые называют пространственными кривыми.
В геометрическом черчении плоские кривые делят на две группы в зависимости от инструментов, которыми выполняется их построение: коробовые (циркульные) кривые, состоящие из дуг окружностей, и лекальные кривые, которые строят по точкам и обводят по лекалу.
КОРОБОВЫЕ КРИВЫЕ ЛИНИИ
Коробовые кривые представляют собой линии, состоящие из сопряженных дуг окружностей разных радиусов. К таким кривым относятся завитки, овалы и овоиды. Коробовые линии получили такое название потому, что такие формы имели днища коробов. Профили кулачков, эксцентрики, фланцы, строительные элементы (арки, своды) в очертаниях имеют эти линии.
Завиток представляет собой плоскую кривую, по форме похожую на спираль и состоящую из нескольких дуг различных радиусов, проведенных из нескольких центров.
Рассмотрим построение четырехцентрового завитка. Заданы четыре центра.(1, 2,3 и 4), которые являются вершинами квадрата со стороной d. Продолжим стороны квадрата, как показано на рис. 156. Из центра 1 радиусом d проводят дугу от точки 4 до пересечения с продолженной стороной квадрата 1 2 в точке А. Из центра 2 радиусом 2А (2d) проводят дугу от точки А до пересечения с продолженной стороной квадрата 2 3 в точке В. Из точки 3 радиусом 3В (3d) проводят дугу от точки В до пересечения с продолженной стороной квадрата 3 4 в точке С. Из центра 4 проводят дугу радиусом 4С (4d) от точки С до пересечения с продолженной стороной квадрата 1 4 в точке D. Далее построение продолжают в той же последовательности, увеличивая радиус дуги каждый раз на величину d. 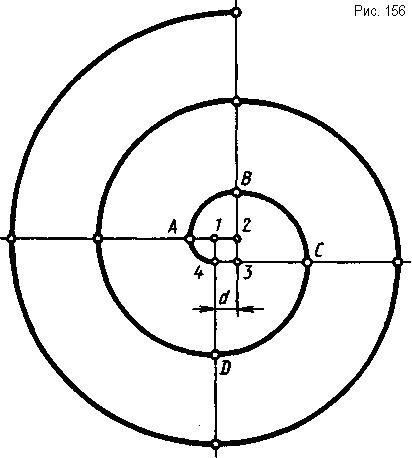
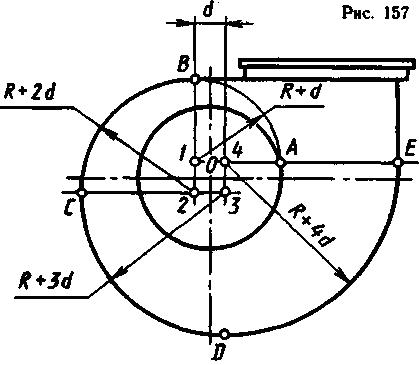
При вычерчивании завитков не всегда начинают построение от вершины квадрата. В чертеже кожуха вентилятора (рис. 157) завиток строят от точки А радиусом R+d из центра 1, где радиус R задается конструктором, до пересечения с продолженной стороной квадрата 2 1 в точке В. Далее из центра 2 проводится дуга радиусом R+2d от точки В до пересечения с продолжением стороны квадрата 3 2 в точке С и т. д. Заканчивается построение завитка в точке Е.
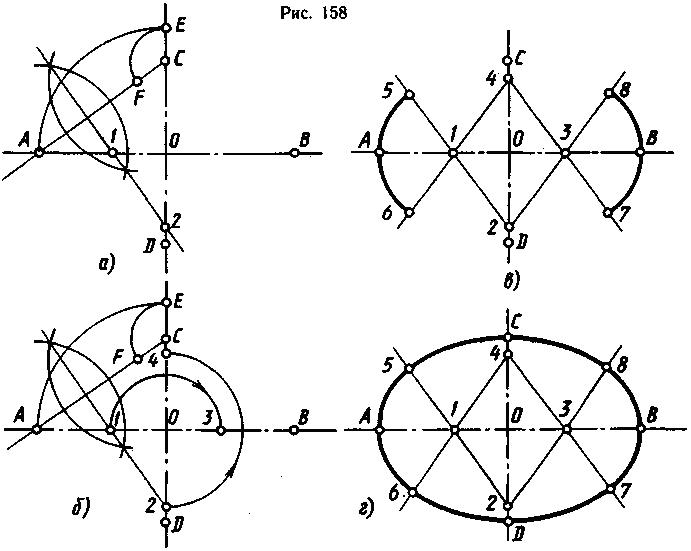
Овал представляет собой плавную замкнутую симметричную кривую, состоящую из четырех сопрягающихся дуг. Для его построения нужно найти четыре центра дуг и четыре точки сопряжения.
По форме овал приближается к эллипсу (лекальная кривая), поэтому эллипс часто заменяют овалом, так как вычерчивать овал проще. Овал имеет две оси: большую и малую. Они делят его на симметричные части. Существует несколько способов построения овалов с четырьмя центрами. Чаще всего строят овал по двум заданным осям.
Заданы две оси: АВ - большая ось и CD - малая ось. Оси взаимно перпендикулярны, поэтому сначала проводят две взаимно перпендикулярные линии и на них откладывают размеры заданных осей (рис. 158, а). Точки А и С соединяют прямой линией. Из точки О радиусом ОА проводят дугу до пересечения с вертикальной линией в точке Е. Отрезок СЕ является разностью полуосей. Этот отрезок откладывают на отрезке АС от точки С, получают точку F. Через середину отрезка AF проводят перпендикулярную прямую (для этого применяют способ деления отрезка пополам циркулем), которая пересечет большую ось в точке 1, а малую - в точке 2. Точка 1 будет центром левой малой дуги, а точка 2 - центром верхней большой дуги. Так как овал - фигура симметричная, то справа от точки О на расстоянии, равным отрезку 01, находится точка 3 - центр правой малой дуги, а сверху на расстоянии, равным отрезку 02, находится точка 4 - центр нижней большой дуги (рис. 158,б).
Поскольку точки сопряжения лежат на прямых, соединяющих центры дуг, точки 1 и 4,3 и 4, 1 и 2, 2 и 3 соединяют прямыми (рис. 158, в). Эти прямые ограничивают длину дуг и на них будут находиться точки сопряжения.
Для построения овала из центров 1 и 3 проводят дуги радиусом, равным отрезку 1А, до пересечения с прямыми в точках 5,6,7 и 8, которые будут являться точками сопряжения. Из центра 2 через точку С радиусом, равным отрезку 2С, проводят дугу от точки 5 до точки 8 (рис. 158, г). Из центра 4 через точку D радиусом, равным 4D, проводят дугу от точки 6 до точки 7.
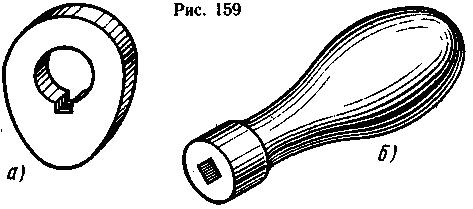
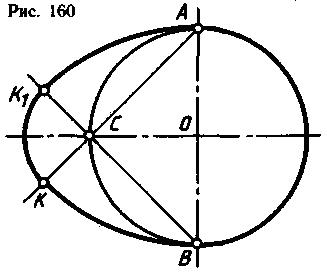
Овоид представляет собой овал, имеющий одну ось симметрии. Эта кривая применяется при вычерчивании кулачков (рис. 159, а), рукояток (рис. 159,б) и других деталей. Овоид задают диаметром или радиусом основной окружности. Построение начинают с проведения оси овоида и центровой линии АВ основной окружности (рис. 160). Точка С будет центром малой дуги овоида. Точки А и В - центры больших дуг овоида. Для нахождения точек сопряжения К и К1 проводят прямые через центры (А, В и С) дуг сопряжения. Из точки А радиусом АВ, равным диаметру заданной окружности, проводят дугу до пересечения с прямой АС в точке К. Из точки В радиусом В А проводят вторую дугу до пересечения с прямой ВС в точке К1. К и K1- точки сопряжения. Из центра С радиусом СК проводят дугу КК1. Дугу АВ проводят радиусом основной окружности.
ЛЕКАЛЬНЫЕ КРИВЫЕ
Лекальные кривые называют так потому, что они обводятся по лекалу. Принадлежащие им точки не лежат на окружностях или дугах, их строят по определенным законам, соединяют тонкой плавной линией от руки и обводят по лекалу небольшими участками. Приемы обводки кривых линий по лекалу подробно рассмотрены в § 2.
В технике часто встречаются детали, имеющие сложные очертания, состоящие из различных криволинейных участков, в том числе и из лекальных кривых. На рис. 161 показаны такие детали: маховое колесо, гайка, кронштейн, кулачок.
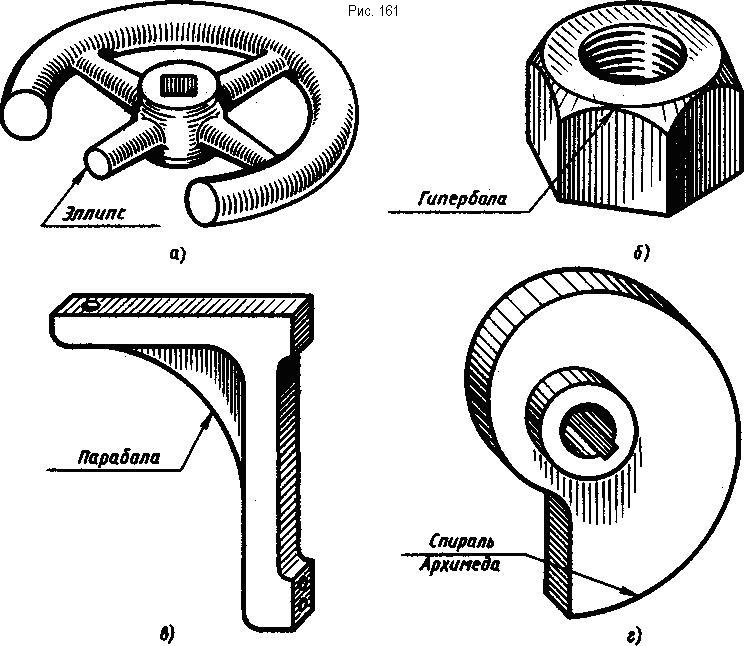
Лекальные кривые получаются при пересечении поверхностей плоскостями, при перемещении какой-либо точки в плоскости по определенному закону, могут графически отражать закономерности какого-либо процесса, являться проекциями пространственных кривых и т. п. По характеру образования лекальные кривые можно разделить: на кривые конического сечения, циклические кривые, спирали, синусоидальные кривые. Рассмотрим несколько кривых из каждой группы.
К р и в ы е к о н и ч е с к о г о с е ч е н и я - эллипс, параболу, гиперболу - можно получить при пересечении прямого кругового конуса плоскостями различного положения по отношению к образующим и оси конуса.
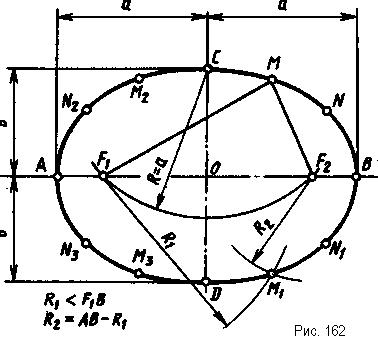
Э л л и п с - это плоская кривая линия, у которой сумма расстояний от любой точки этой кривой до двух ее фокусов (F1 и F2), расположенных на большой оси, есть величина постоянная, равная большой оси эллипса. Например, сумма расстояний от точки М до двух фокусов F1, F2 (рис. 162) равна величине большой оси эллипса АВ, то есть F1M+F2M=AB. Эллипс всегда имеет две взаимно перпендикулярные оси (большую и малую). На рис. 162 дана большая ось АВ = 2а и малая ось CD = 2b, требуется построить эллипс, используя для этого его фокусы. Сначала находят два фокуса F1 и F2. Для этого из точек С или D проводят дугу радиусом R=a до пересечения с большой осью в точках F1 и F2. Эти точки являются фокусами, так как точка С принадлежит эллипсу, a CF1+CF2=AB по построению. Для построения точек М, М1, M2, Мз произвольным радиусом R1 (R1 не больше расстояния F1B) сначала из фокуса F1, а потом из фокуса F2 сверху и снизу от большой оси проводят небольшие дуги. Второй радиус (R2) равен разности AB-R1. Радиусом R2 из двух фокусов делают засечки на четырех ранее проведенных дугах, получают точки М, М1, M2 и М3. Число точек для построения очертания эллипса берется по необходимости, и все они строятся аналогично точкам М, М1, М2 и М3.
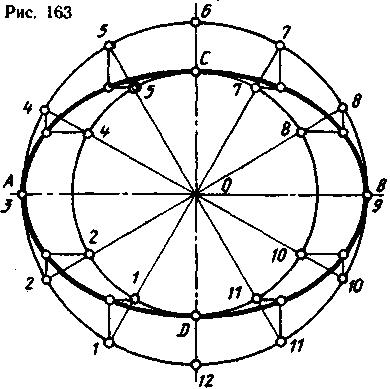
Построение эллипса по заданным осям. Заданы оси эллипса АВ (большая) и CD (малая), требуется построить эллипс. Проводят две взаимно перпендикулярные Прямые и от точки их пересечения (точка О) откладывают вверх) и вниз по половине малой оси, а влево и вправо- по половине большой оси (рис. 163). Из точки О описывают две концентрические окружности: одну - через концы малой оси, а вторую - через концы большой оси. Большую окружность делят на любое число равных частей, например, двенадцать, все точки деления соединяют прямыми с точкой О. Эти двенадцать радиусов разделяют малую окружность тоже на двенадцать равных частей. Из всех двенадцати точек, лежащих на большой окружности, проводят прямые, параллельные малой оси, а из точек, лежащих на малой окружности, проводят прямые, параллельные большой оси эллипса, до пересечения друг с другом. В пересечении этих прямых получают точки, принадлежащие эллипсу. Затем эти точки соединяют от руки плавной линией и обводят по лекалу.
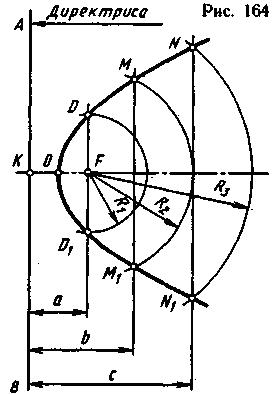
П а р а б о л а - это плоская кривая, каждая точка которой удалена на одинаковое расстоя-ние от заданной точки F (фокус) и заданной прямой АВ (директриса). Парабола имеет одну ось симметрии. Между директрисой и фо-кусом задается расстояние. Вершина параболы (точка О) всегда находится посередине этого расстояния, потому что она, как и любая точка параболы, должна находиться на одинаковом расстоянии от фокуса и директрисы. На рис. 164 показано построение параболы, где задано расстояние между директрисой и фокусом (отрезок KF). Через точку К проводят директрису, параллельно директрисе произвольно проводят несколько прямых. Первая прямая проведена через фокус F. Из точки F радиусом R1=а проводят дугу до пересечения с прямой в точ-ках D и D1. Эти точки будут принадлежать параболе, так как они находятся на одинаковом расстоянии (а) от директрисы и фокуса. Вторая прямая проведена на расстоянии b от директ-рисы. Из точки F проводят дугу радиусом R2=b до пересечения с этой прямой в точках М и M1, которые будут принадлежать параболе, так как находятся на одинаковом расстояний (b) от директрисы и фокуса, и т. д.
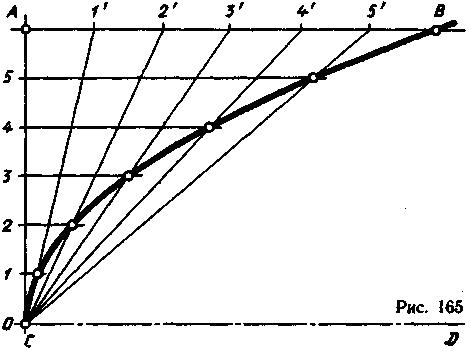
Существует несколько способов построения параболы. Рассмотрим два из них.
Построение параболы по оси CD, вершине О и точке В, принадлежащей параболе. Из вершины параболы (точка О) перпендикулярно оси CD параболы проводят прямую. Из точки параллельно оси проводят прямую до пересечения с первой прямой в точке А (рис. 165). Отрезки ОА и АВ делят на одинаковое число равных частей, затем полученные точки нумеруют от вершины О на вертикальной прямой от точки А на горизонтальной прямой. Вершину О соединяют с точками на прямой АВ. Из точек, лежащих на прямой О А, проводят прямые параллельно оси параболы: из точки 1 - до пересечения с прямой О1, из точки 2 - до пересечения с прямой 02 и т. д. Точки пересечения будут точками параболы (рис. 165).
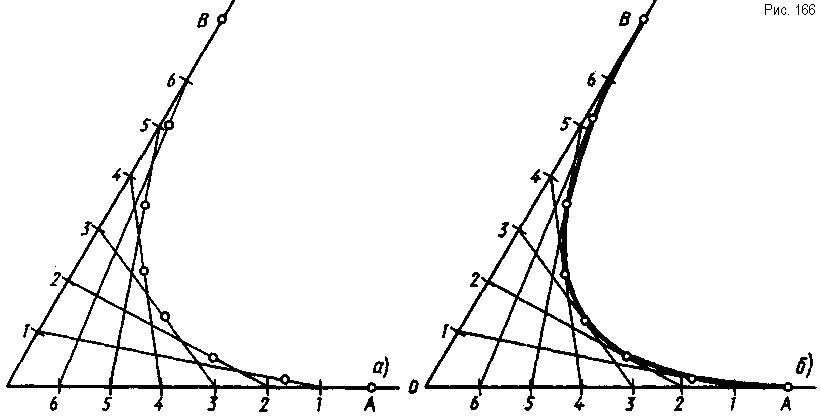
Построение параболы как кривой, касательной к двум прямым с заданными на них точками касания А и В. Построение начинают с деления отрезков О А и ОВ на одинаковое число равных частей. Затем на одной прямой от точки О, а на другой прямой от точки А полученные точки нумеруют (рис. 166, а). Точки с одинаковым номером соединяют прямыми, которые, пере-секаясь между собой, как бы скругляют угол А0В ломаной линией. Примерно посередине каждого отрезка этой линии находится точка, принадлежащая параболе. Эти точки соединяют от руки тонкой плавной линией и обводят по лекалу (рис. 166,б).
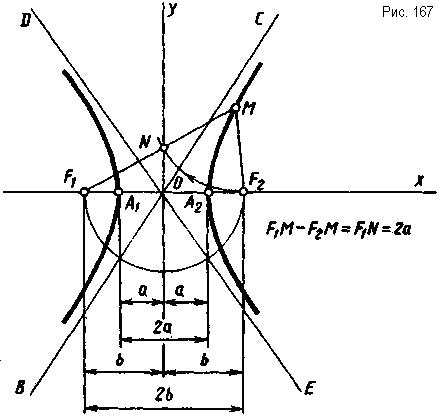
Г и п е р б о л а - это плоская кривая, разность расстояний от каждой точки которой до двух заданных точек F1 и F2 (фокусов) есть величина постоянная, равная расстоянию между вершинами гиперболы А1 и А2. Гипер-бола имеет две незамкнутые симметрично расположенные ветви (рис. 167). Она имеет две асимптоты (ВС и DE) - прямые, к которым ветви гиперболы стремятся приблизиться, но это приближение бесконечно. Гипербола имеет две оси - действительную (х) и мнимую (у). На действительной оси располагаются два фокуса (F1 и F2), вершины (А1 и А2) и центр гиперболы (точка О), который находится посередине отрезка А1А2. На рис. 167 на примере произвольно взятой точки М показано, что разность расстояний от этой точки до фокусов (F1 и F2), т. е. отрезок F1N, равна отрезку А1А2 - расстоянию между вершинами гиперболы.
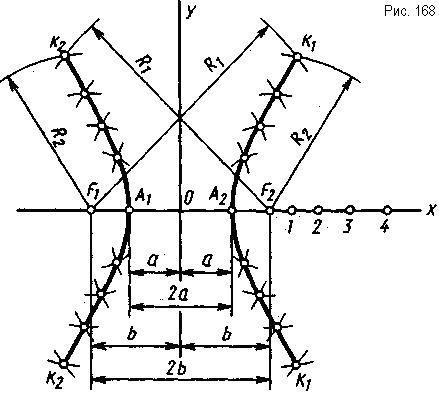
Построение гиперболы по заданным фокусам и вершинам. Заданы расстояние между фокусами F1 и F2 (2Ь) и расстояние между вершинами (2а), требуется построить две ветви гиперболы. Для построения сначала проводят действительную ось х и мнимую ось у (рис. 168). В их пересечении лежит центр гиперболы (точка О), от которого откладывают влево и вправо расстояния а и b, т. е. строят фокусы F1 и F2 и вершины А1 и Аз. Затем от одного из фокусов, например F2, по действительной оси (в данном случае вправо) откладывают несколько отрезков произвольной длины так, чтобы по мере удаления от фокуса их величина несколько увеличивалась. На рис. 168 отложено четыре таких отрезка, концы которых отмечены цифрами 1, 2,3, 4. Из фокусов F1 и F2 поочередно проводят дуги радиусом, равным расстоянию от построенных точек до вершин А1 и А2. Рассмотрим это на примере построения точек К1 и К2. Радиусом R1, равным расстоянию от точки 4 до точки А1, из фокуса F1 проводят сверху и снизу по небольшой дуге. Тем же радиусом R1 из фокуса F2 проводят еще две дуги. Затем радиусом R2, равным расстоянию от точки 4 до точки А2, из фокусов F1 и F2 поочередно делают засечки на первых четырех дугах, в пересече нии получают точки К1 и К2. Таким же образом от точек 1,2 и З получают радиусы для построения других точек гиперболы.
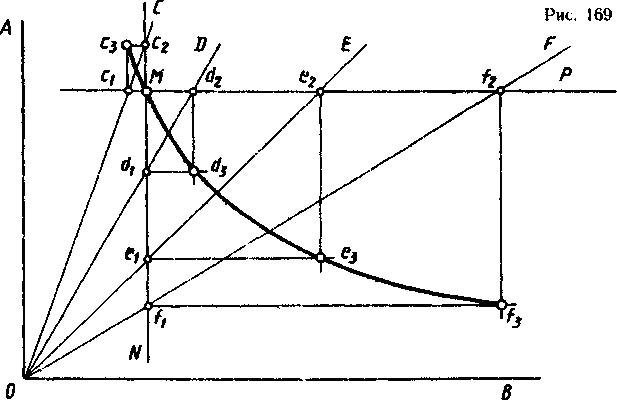
Построение равнобокой гиперболы по заданным асимптотам ОА и ОВ и точке М (рис. 169). Через заданную точку М параллельно асимптотам проводят две прямые. Из точки О проводят произвольно прямые ОС, OD, OE, OF, как показано на рис. 169, каждая из которых пересекает прямые, проведенные параллельно асимптотам, в двух точках (с1 с2, d1, d2...). Из построенных точек проводят прямые, параллельные асимптотам, как показано на рис. 169, в пересечении которых получают точки, принадлежащие гиперболе (с3, d3, е3 и f3). Затем эти точки соединяют плавной тонкой линией от руки и обводят по лекалу.
Ц и к л и ч е с к и е к р и в ы е - это плоские линий, которые получаются в результате перемещения точки окружности, катящейся по какой-либо линии. Катящаяся окружность, на которой лежит точка, является производящей окружностью, а окружность или прямая, по которой катится окружность,- направляющей. К циклическим кривым относятся циклоида, эпициклоида, гипоциклоида. Эти кривые широко применяются в машиностроении в деталях, обычно связанных с круговым движением, например, в построениях профиля зуба зубчатых колес и реек.
Циклоида (от греч. kykloeides - кругообразный) - плоская кривая, описываемая точкой окружности, которая без скольжения катится по прямой линии.
Заданы направляющая прямая CD и производящая окружность радиуса R с лежащей на ней точкой К, исходное положение которой К0 (рис. 170). Проследим, какой путь пройдет точка К за один полный оборот окружности, катящейся по прямой CD. Это будет полный цикл кривой. Окружность за это время пройдет по прямой путь, равный длине развернутой окружности, т. е. L=2nR. Точка К после одного оборота окружности снова окажется на прямой CD в точке К8.
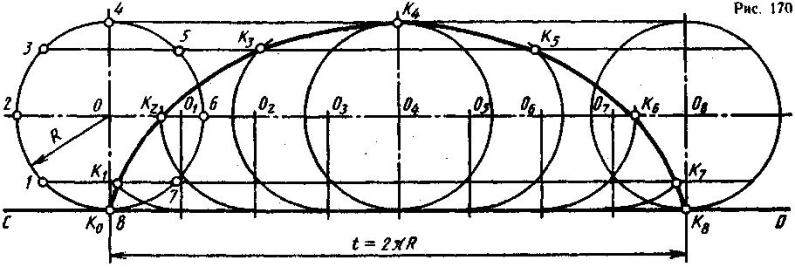
Для определения промежуточных положений точки К через равные промежутки фиксируют положение этой точки. Для этого делят окружность на любое число равных частей, например, на восемь, получают точки 1...8 (рис. 170), проводят из точки О линию центров, на которой отмечают восемь промежуточных положений центров (O1...O8) производящей окружности, разделив L=2nR на восемь равных частей.
Когда окружность пройдет 1/8 своего пути, точка К сместится вправо и вверх и окажется над направляющей прямой CD на такой же высоте, на которой находится точка 1. Поэтому для построения промежуточной точки К1 из точки 1 проводят прямую, параллельную CD, а из центра 01 описывают часть окружности в ее промежуточном положении радиусом R до пересечения с этой прямой.
Это и будет первое промежуточное положение точки К. Аналогично строят остальные точки. Соединив точки К0...К8 плавной тонкой линией от руки, получают циклоиду, которую обводят по лекалу.
Эпициклоида - плоская кривая, описываемая точкой производящей окружности, которая без скольжения катится по направляющей окружности, при этом производящая и направляющая окружности имеют внешнее касание.
Заданы окружности радиусов R и R1. На производящей окружности радиуса R, в месте касания двух окружностей, лежит точка Ко.
Окружность радиуса R1 является направляющей. При качении производящей окружности радиуса R по направляющей окружности радиуса R1 точка К за один полный оборот катящейся окружности опишет один цикл кривой и переместится из положения Ко в положение К8. Для построения одного цикла кривой достаточно провести не всю окружность радиуса R1, а только ее часть (рис. 171). Для построения промежуточных положений точки К окружность радиуса R делят на равные части, например на восемь, 1/8 длины окружности радиуса R откладывают по направляющей дуге радиуса R1 от точки Ко восемь раз.
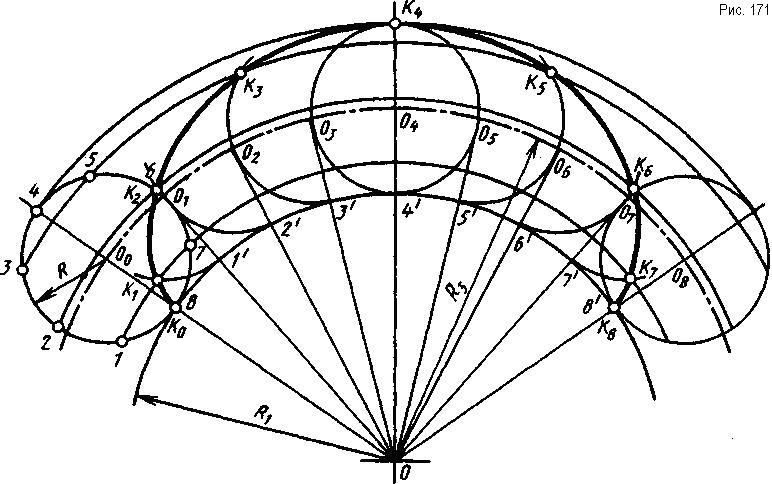
Через полученные точки (1'. .8') и центр О проводят прямые до пересечения с дугой радиуса Rз, получаются промежуточные центры окружности R (О1...О8). Из центра О через точки 4, 3, 2, 1 проводят дуги до пересечения с дугами, проведенными из соответствующих центров О1...О8, радиусом R, получают точки К1...К8, принадлежащие эпициклоиде. Соединив точки Ко...К8 тонкой линией, получают эпициклоиду, которую обводят по лекалу.
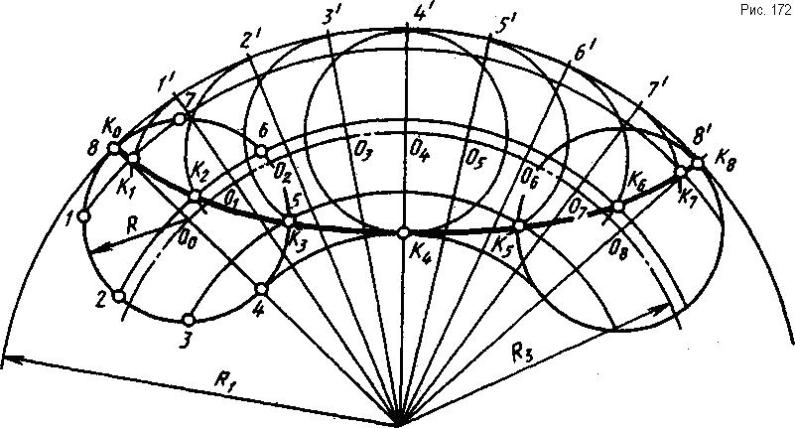
Г и п о ц и к л о и д а - плоская кривая, описываемая точкой производящей окружности, которая без скольжения катится по направляющей окружности, при этом направляющая и производящая окружности имеют внутреннее касание.
Построение гипоциклоиды аналогично построению эпициклоиды (рис. 172), только в этом случае производящая окружность радиуса R катится с внутренней стороны направляющей окружности радиуса R1 и все построения будут находиться внутри направляющей окружности.
С п и р а л ь - плоская кривая, описываемая точкой, которая вращается вокруг неподвижного центра и одновременно удаляется от него в соответствии с определенной закономерностью.
Спирали широко используются в технике при конструировании зажимных эксцентриковых приспособлений, в кулачковых патронах и механизмах, при конструировании фрез, при изготовлении плоских пружин и т. п.
С п и р а л ь А р х и м е д а - кривая, образованная движением точки, равномерно движущейся по прямой, которая, в свою очередь, равномерно вращается в плоскости вокруг неподвижной точки, принадлежащей этой прямой. Характер спирали Архимеда определяется шагом t, т. е. расстоянием, которое пройдет точка по прямой за один полный оборот этой прямой на 360°. Вращение прямой может происходить как по часовой стрелке, так и против.
Рассмотрим способ построения спирали Архимеда с шагом t и вращением прямой по часовой стрелке. Чтобы построить спираль, необходимо зафиксировать несколько промежуточных положений точки и прямой, по которой она перемещается. Для этого вспомогательная окружность, проведенная радиу-сом, равным t и отрезок 08, равный шагу, делятся на одинаковое число равных частей, например, на восемь (рис. 173). Начальная точка (Ко) совпадает с точкой О. Отрезок 08, по которому движется точка, вращается так, что один конец (точка О) неподвижен. При повороте отрезка на 1/8 полного угла (45°) точка К пройдет 1/8 своего пути. Поэтому если из центра О радиусом 01 провести дугу до пересечения с прямой, проведенной через точку и центр О, получим точку К1 принадлежащую спирали. Если провести дугу радиусом 02 до пересечения с прямой 02', получится точка К2, принадлежащая спирали, и т. д. При полном обороте отрезка 08 вокруг точки О отрезок совпадает со своим начальным положением, а точка К займет положение К8. Полученные точки К0...К8 соединяют плавной линией, которую обводят по лекалу.
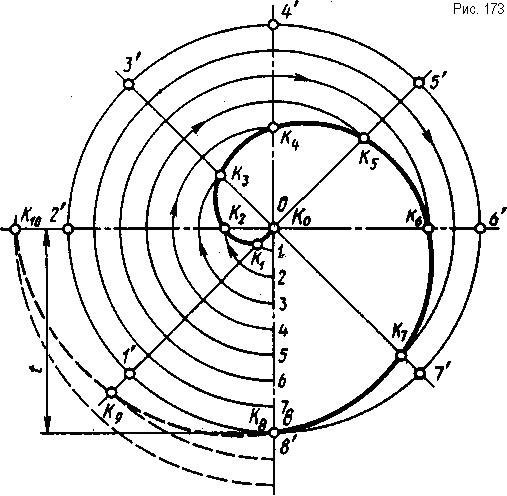
При вычерчивании следующего витка спи-рали построение продолжают таким же образом, увеличивая радиус на 1/8 шага. На рис. 173 это показано штриховой линией. Дальнейшее построение можно выполнить и другим способом. Для этого от точек К0...К8 откладывают по прямым O1' ...08' отрезок, равный шагу t, получают точки К0..К16.
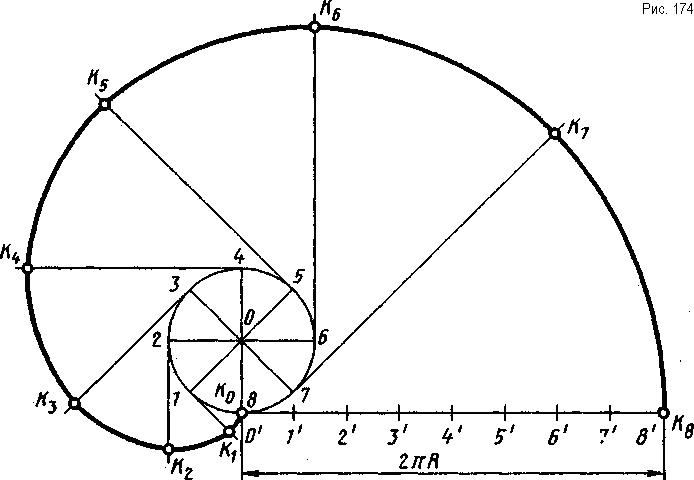
Э в о л ь в е н т а о к р у ж н о с т и - плоская кривая линия, представляющая собой траекторию точки окружности при ее развертывании. Слово "эвольвента" - латинское, означает "развертывающий".
Эвольвенту окружности можно получить, если поверхность цилиндра обернуть упругой проволокой в один полный оборот и закрепить один ее конец. Отпущенный второй конец, развертываясь (распрямляясь в отрезок), опишет в пространстве кривую, которая и будет эвольвентой. При этом длина проволоки будет равна длине окружности основания данного цилиндра (2лR).
Такую же кривую описывает любая точка прямой линии, катящейся без скольжения по окружности. Эвольвента используется припрофилировании кулачков, эксцентриков, зубьев зубчатых передач и т. п.
Если окружность разделить на любое число равных дуг и представить развертывание и выпрямление каждой дуги в отрезок прямой Минин, то полученные отрезки будут касательными к заданной окружности. Точки касания будут точками окончания каждой дуги, которые будут одновременно начальными точками следующих дуг. А как известно, касательная перпендикулярна к радиусу окружности, проведенному в точку касания.
На рис. 174 показано построение эвольвенты окружности. Заданную окружность делят на любое число равных дуг (в данном случае на восемь), получают точки 1...8. Каждую точку деления соединяют с центром окружности (точка О). Из точки 8 проводят касательную к окружности и откладывают на ней длину окружности (2пR). Этот отрезок будет развернутой окружностью. Точка 8' будет принадлежать эвольвенте. Затем полученный отрезок делят на восемь равных частей и получают отрезки, равные '/8 длины окружности, для определения длины каждой развернутой дуги. Далее через точки 1...8 проводят касательные и откладывают отрезки, равные длине соответствующей дуги. От точки 1 откладывают отрезок, равный длине развернутой дуги 0'1'. От точки 2 - отрезок, равный длине развернутой дуги 0'2' и т. д. Получают точки К1...К8, принадлежащие эвольвенте. Полученные точки соединяют плавной кривой линией, которую обводят по лекалу.
С и н у с о и д а - плоская кривая линия, изображающая изменение синуса в зависимости от изменения угла а. Она используется в построении проекций винтовых линий.
На рис. 175 показано построение синусоиды. Прямая Ох - ось синусоиды, t - шаг или длина волны. На рис. 175 t=2πR. Если t=2πR, синусоида называется нормальной; при t<2πR синусоида сжатая; при t>2πR синусоида растянутая. Высшая и низшая точки синусоиды называются вершинами. На рис. 175 это точки К2 и К6.
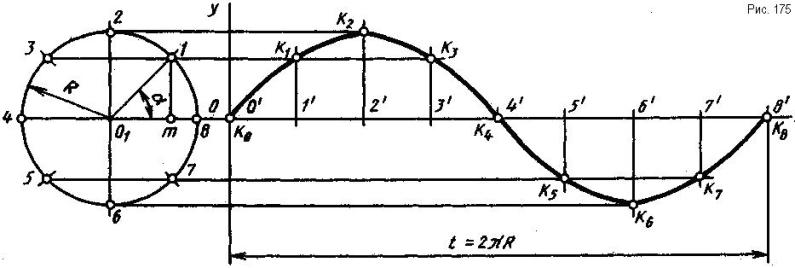
Для построения синусоиды проводят оси координат Ох и Оу. На некотором расстоянии слева от точки О проводят окружность заданного радиуса R. Вправо от точки О, по оси Ох, откладывают отрезок t - заданный шаг (в данном случае t=2πR). Окружность и отрезок t делят на одинаковое число равных частей (на рис. 175- на восемь равных частей). Из точек деления отрезка проводят перпендикуляры, на которых откладывают отрезки, равные соответствующим полухордам (1t, 012 и т. д.). Для этого из точек 1...8 деления окружности проводят прямые, параллельные оси Ох, до пересечения с перпендикулярами из соответствующих точек 1'...8' деления отрезка t, получают точки К1...К8. Эти точки принадлежат синусоиде. Их соединяют от руки тонкой плавной линией, которую обводят по лекалу.
Дата: 2018-12-21, просмотров: 2690.