Деление отрезка пополам рассматривалось в §9 (см. рис. 102).

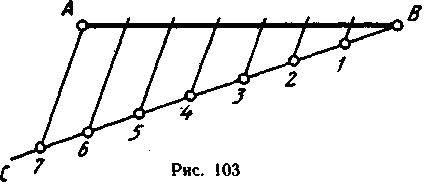
Если отрезок, например отрезок АВ (рис. 103), необходимо разделить на несколько равных частей, то из любого конца заданного отрезка под произвольным острым углом проводят вспомогательную прямую ВС. От вершины образовавшегося угла (в данном случае от точки В) на вспомогательной прямой откладывают столько одинаковых отрезков произвольной длины, на сколько частей требуется разделить отрезок АВ. Конец последнего отрезка соединяют прямой линией с точкой А и параллельно этой линии через все деления проводят прямые до пересечения с прямой АВ, деля ее тем самым на заданное число равных отрезков.

ПОСТРОЕНИЕ И ДЕЛЕНИЕ УГЛОВ

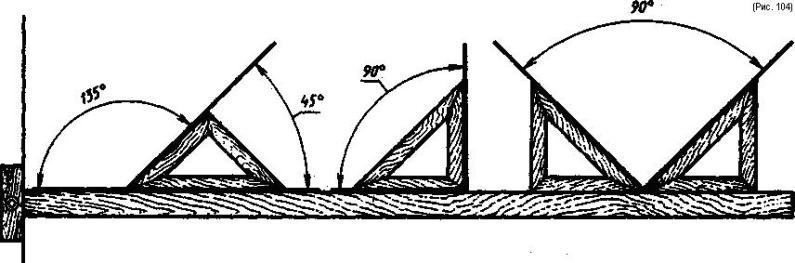
С помощью рейсшины и угольника с углами 45, 45 и 90° строят углы: 45, 90 и 135° (рис. 104).

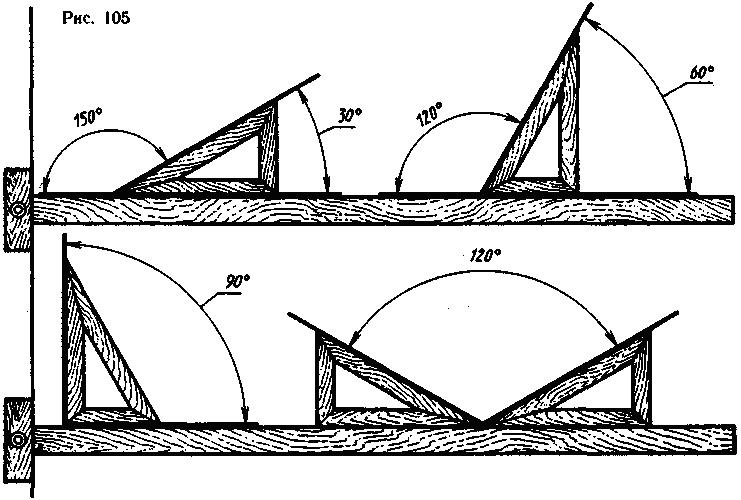
С помощью рейсшины и угольника с углами 30, 60 и 90° можно построить углы: 30, 60, 90, 120 и 150° (рис. 105).

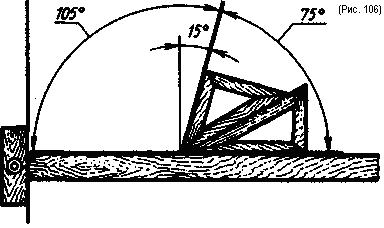
Используя два угольника и рейсшину, можно построить углы: 15° от вертикальной прямой, 75 и 105° (рис. 106).

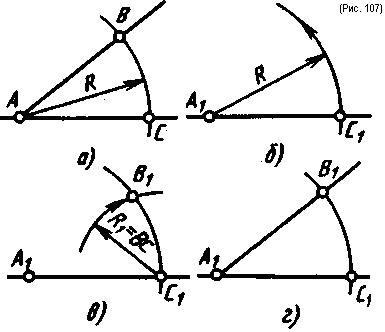
П о с т р о е н и е у г л а, р а в н о г о д а н н о м у, выполняется с помощью циркуля (рис. 107). Из вершины А заданного угла ВАС произвольным радиусом R проводят дугу до пересечения со сторонами угла в точках В и С (рис. 107, а). В том месте чертежа, где нужно построить угол, равный данному, проводят прямую линию (в данном случае горизонтальную). На ней задают точку А₁ (вершину угла). Из точки А₁ радиусом R, равным АВ или АС, проводят дугу до пересечения с прямой, получают точку С₁ (рис. 107, б). Из точки С₁ радиусом R₁, равным отрезку ВС, делают на дуге засечку, тем самым находят точку В₁ (рис. 107, в). Соединив точки А₁ и В₁, получают угол В₁А₁С₁, равный данному (рис. 107, г).

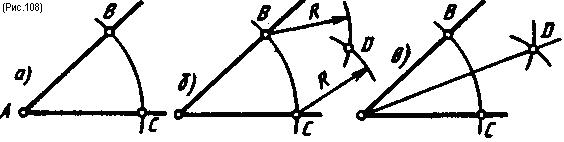
Деление угла пополам выполняется циркулем. Из вершины угла произвольным радиусом проводят дугу до пересечения ее со сторонами угла, получают точки В и С (рис. 108, а). Затем из точек В и С проводят две дуги радиусом больше половины расстояния ВС (рис. 108, б) до их пересечения в точке D. Соединив точки А и D прямой, получают биссектрису угла, которая делит угол пополам (рис. 108, в).

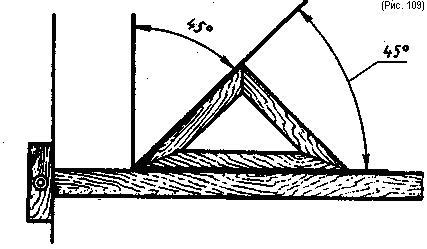
Деление прямого угла пополам с помощью угольника с углами 45, 45 и 90° и рейсшины Доказано на рис. 109.

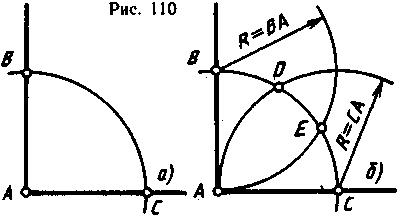
Д е л е н и е п р я м о г о у г л а н а т р и р а в н ы е ч а с т и выполняется циркулем или с помощью угольника и рейсшины. При делении угла циркулем из вершины А произвольным радиусом проводят дугу до пересечения со сторонами угла в точках В и С (рис. 110, а). Затем тем же радиусом из точек В и С делают да дуге засечки, получают точки D и Е (рис. 110, б), которые соединяют с точкой А. прямые АЕ и AD делят прямой угол на три равные части (рис. 110, в).

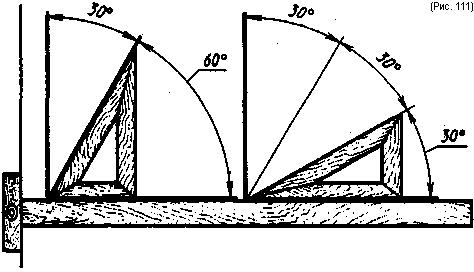
Деление прямого угла на три равные части с помощью рейсшины и угольника с углами 30, 60 и 90° показано на рис. 111.

ПОСТРОЕНИЕ ПЛОСКИХ ФИГУР

П о с т р о е н и е м н о г о у г о л ь н и к а, р а в н о г о д а н н о м у, можно выполнить так, что его стороны будут располагаться параллельно соответствующим сторонам заданного многоугольника, или построенный многоугольник будет повернут в плоскости относительно заданного. И в том, и в другом случае решение задачи сводится к построению третьей точки относительно двух заданных.

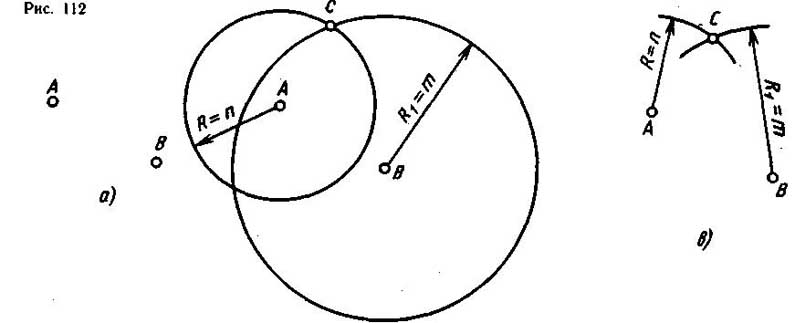
Например, на плоскости заданы точки А и В (рис. 112, а). Требуется построить точку С, расположенную выше заданных точек на расстоянии n от точки А, и m от точки В. Множество точек, которые находятся на расстоянии n от точки А, располагается на окружности с центром в точке А радиусом R=n. Множество точек, которые располагаются на расстоянии m от точки В, находится на окружности с центром в точке В радиусом R₁=m (рис. 112, б). В пересечении этих окружностей получают точки С и С₁. Из двух полученных точек выбирают нужную. Проводить окружности полностью не обязательно, достаточно провести две короткие дуги (рис. 112, в).

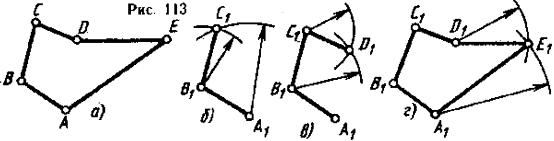
На рис. 113, а задан многоугольник ABCDE. Требуется построить равный ему многоугольник A₁B₁C₁D₁E₁. Построение многоугольника A₁B₁C₁D₁E₁ можно начать с построения любой его стороны, например стороны АВ. Для этого параллельно стороне АВ проводят, прямую и на ней циркулем откладывают отрезок А₁В₁, равный отрезку АВ. Затем циркулем измеряют расстояние от точки А до точки С и этим радиусом из точки А проводят дугу в направлении строящейся точки С, также от точки В измеряют расстояние до точки С и этим радиусом из точки В проводят дугу до пересечения с первой дугой в точке С. Соединив точку С с точкой В прямой линией, получают вторую сторону многоугольника ВС (рис. 113, б). Для построения точки D измеряют расстояние от точки D до двух других вершин многоугольника (например А и В, или В и С, или С и А). На рис. 113, в взяты расстояния от точек В и С. Дугу из точки В проводят радиусом, равным отрезку BD, а из точки С - радиусом, равным отрезку CD. Пересечение этих дуг дает точку D. Соединив точку D с точкой С, получают сторону многоугольника CD (рис. 113, в). Аналогично строят точку Е (рис. 113, г).