Все переменные программы соответствуют переменным, которые введены в схеме алгоритма. Дополнительно определим их типы.
| | n — параметр ряда; по условиям задачи это — целое число; поскольку заранее неизвестно, сколько итераций цикла будет нужно для достижения предела точности, объявим его как "длинное целое": long n; Отметим, что хотя по условию задания n — целое, результаты выражений, в которых фигурирует n, будут иметь дробную часть. Преобразование типов можно выполнять непосредственно при вычислении выражения, но чтобы заранее исключить ошибки, введем еще одну переменную— dbln, которая будет представлять значение n как числа с плавающей точкой: double dbln; term — значение текущего члена ряда. Объявим его как: double term; sum — текущее значение суммы ряда с начальным значением 0. Объявим его как: double sum=0; |
k2 — переменная для сохранения текущего значения 2n с начальным значением 1 (см. пп.5.1.2). Она должна быть "длинным целым" — из тех же соображений, что и n:
long k2=1;
k1 — переменная для сохранения текущего значения (–1)n с начальным значением 1 (см. пп.5.1.3). Для нее достаточно быть "коротким целым":
short k1=1;
eps — переменная для представления заданного предела точности. Она должна иметь начальное (неизменное) значение 0.000001, поэтому может быть объявлена как const. Использование переменной для представления константы вместо употребления константы непосредственно в операторах программы может повысить гибкость программы:
const double eps=0.000001;
Разработка текста программы
Начинаем разработку текста программы с заголовка главной функцииmain ():
int main(void)
Далее открывается тело функции, и в него включаются определения переменных (см. п.5.2). Определения переменных реализуют блок 2 блок-схемы алгоритма. В дополнение к переменным, определенным в схеме алгоритма, объявляем рабочую переменную dbln и константу eps. Поскольку правила языка C позволяют присваивать переменным начальные значения, в объявлении переменных отчасти реализован также и блок 3. Блоки 4–9 схемы алгоритма образуют цикл. В языке С есть два "простых" оператора цикла: цикл с предусловием — whіle и цикл с постусловием — do-whіle. Но по схеме алгоритма видно, что выход из цикла происходит в середине тела цикла (блок 5): после вычисления члена ряда, но до добавления его значения к сумме. Следовательно, "простые" циклы применить нельзя. "Сложный" оператор цикла— for — является циклом с предусловием, но задавать условие в самом операторе цикла необязательно. К тому же этот оператор дает возможность определить действия, которые нужно выполнить до начала цикла и действия, которые выполняются в конце каждой итерации. Таким образом, открытие цикла будет иметь вид:
for (n=0; ; n++, k2*=2, k1=-k1) {
где первый параметр for — присваивание начального значения переменной n (остаток блока 3), второй параметр — условие выхода из цикла — пустой, третий параметр реализует блок 8 схемы алгоритма. В теле цикла содержится несколько отдельных действий, значит, будет несколько операторов, поэтому тело цикла берется в операторные скобки.
В теле цикла первый оператор: dbln=n;
это действие не предусмотрено в схеме алгоритма, но его необходимость пояснили в п.5.2.
Далеевычисляется значениетекущего члена ряда:
term = k 1*( dbln +1)/( dbln * dbln + k 2);
этот оператор полностью реализует блок 4 и формулу из индивидуального задания (учитывая пп.5.1.2, 5.1.3) за исключением того, что вместо операции возведения в степень 2 применяем умножение.
Следующее действие — проверка достижения предела точности — на схеме алгоритма представлена блоком 5 и выполняется условным оператором, который начинается с:
if (fabs(term)>=eps)
Следует отметить, что сравнивается абсолютное значение term, а функция для получения абсолютного значения переменной типа double — fabs(). Эта функция описана в файле math.h, так что нужно включить этот файл в начало программы:
#іnclude <math.h>
Продолжение условного оператора, действие, которое выполняется при выполнении условия, — добавление значения члена к сумме (блок 6):
sum+=term;
При невыполнении условия нужно выйти из цикла, так что условный оператор требует и второй части:
else break;
По схеме алгоритма надо проверить, не достигла ли переменная n значения 9 (блок 7), и, если да, — печатать значение суммы (блок 8). Это реализуется условным оператором:
if ( n ==9) printf ("Сумма 10 член о в ряда=%10.7 lf \ n ", sum );
Поскольку при невыполнении условия не делается ничего, часть else для этого оператора не нужна.
При вызове функции всегда возникает проблема форматизации вывода. включили в формат текст, который поясняет вывод, а значение переменнойsum выводим по спецификации %10.7lf. Тип спецификации соответствует типу переменной — double, а числовые параметры выбрали произвольно, поскольку в задании не оговорены требования к точности вывода. Перед точкой оставляем 2 позиции — для знака и целой части (которая должна быть 0), после точки — 7 позиций, что на 1 превышает точность заданного предела точности. Функция prіntf() описана в файле stdіo.h, поэтому включаем этот файл вначало программы:
#include <stdio.h>
Поскольку блок 9 схеми алгоритма реализован нами в заголовке цикла, то цикл на этом заканчивается, и ставим операторную скобку, закрывающую тело цикла.
Выход из цикла происходит по оператору break в составе условного оператора. После выхода из цикла должны напечатать окончательное значение суммы (блок 10), что и делаем оператором:
prіntf("Повна сума ряду = %10.7lf\n",sum);
При определении формата вывода работают те же соображения, что и в предыдущем случае. Реализация алгоритма закончена, ставим операторную скобку, которая закрывает тело функцииmaіn().
Полный текст программы приведен ниже.
#include <stdio.h> #include <math.h> int main(void) { longn; /* параметрряда */ double dbln ; /* параметр рядав форме с плавающей точокй */ double sum=0; /* сумма членов ряда */ double term; /* значениетекущего члена */ constdouble eps =0.000001; /* пределточности */ long k2=1; /* pow(2,n)*/ short k1=1; /* pow(-1,n)*/ /* основной цикл; в модификациях выисляются следующие значения pow(2,n) и pow(-1,n)*/ for (n=0; ; n++, k2*=2, k1=-k1) { /* преобразование n в форму с плавающей точкой */ dbln=n; /* вычислениеочередного члена */ term = k 1*( dbln +1)/( dbln * dbln + k 2); /* проверкадостиженияпределаточности */ if ( fabs ( term )>= eps ) /* если не досягнут - накопление суммы */ sum+=term; /* если досягнут - выход из цикла */ else break; /* если 10 членов - вывод суммы */ if (n==9) printf(" Сумма 10 членовряда = %10.7lf\n",sum); } /* конец основного цикла */ /* вывод окончательной суммы */ printf("Полная сумма ряда = %10.7lf\n",sum); return 0; }Отладка программы
При отладке программы целесообразно использовать пошаговый режим с отслеживанием значений переменных — прежде всего: n, term, sum. Следует выполнить шаг за шагом несколько итераций цикла, убеждаясь, что эти переменные получают правильные значения. В таком режиме нетрудно выполнить 10 итераций и убедиться в правильном формировании первого результата. Если возникают ошибки при вычислении наиболее сложного выражения в программе:
term=k1*(dbln+1)/(dbln*dbln+k2);
можно включить в программу временные дополнительные переменные и разбить выражение на простые составляющие, проверяя на шаг за шагом значения этих переменных. Например:
double temp1, temp2; /* временныепеременные */ . . . temp1=dbln+1; temp 2= dbln * dbln ; temp2=temp2+k2; temp1=temp1/temp2; term = k 1* temp 1;Для того, чтобы убедиться в правильном выводе второго результата, имеет смысл при отладке выводить вместе с суммой и номер итерации, на котором закончилась робота цикла, и значение члена ряда, которое оказалось меньше предела точности:
printf("%ld %10.7lf\n",n,term);
Лабораторная работа №5
Работа с матрицами
1. Цель работы
2. Темы для предварительной проработки
3. Задание
4. Варианты индивидуальных заданий
5. Пример решения задачи
5.1. Разработка алгоритма решения
5.2. Определение переменных программы
5.3. Разработка текста программы
5.4. Отладка программы
Цель работы
Целью лабораторной работы является получение практических навыков в работе с матрицами в языке C.
2. Темы для предварительной проработки
· Операторы циклаязыка C. Вложенные циклы.
· Условный оператор языка C.
· Матрици.
Задание
Создать квадратную матрицу целых чисел размером 9х9. В индивидуальных заданиях указано, какую обработку матрицы требуется выполнить.
Если по условию задания матрицу следует заполнить случайными числами, рекомендуем выбирать эти числа из диапазона 0 – 99. Если по условию задания в матрицу следует записатьЛП — линейную последовательность чисел, имеется в виду последовательность: 1, 2, 3, ... Программу разработатьсиспользованием меню!!!
Варианты индивидуальных заданий
| Вариант | Содержание задания | Иллюстрация |
| 1 | Заполнить матрицу ЛП, от левого верхнего угла по диагонали: влево — вниз. | 
|
| 2 | Заполнить секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями. | 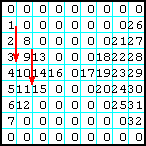
|
| 3 | Заполнить матрицу случайными числами. Отобразить матрицу симметрично относительно побочной диагонали | 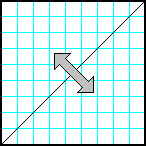
|
| 4 | Заполнить матрицу случайными числами. Отобразить симметрично относительно вертикальной оси секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей. | 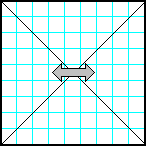
|
| 5 | Заполнить матрицу случайными числами. Отобразить верхнюю половину матрицы на нижнюю зеркально симметрично относительно горизонтальной оси. | 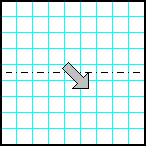
|
| 6 | Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями. | 
|
| 7 | Заполнить матрицу случайными числами. Отобразить главную и побочную диагонали симметрично относительно вертикальной оси. | 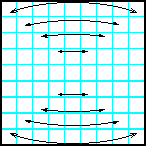
|
| 8 | Заполнить матрицу случайными числами. Разместить на главной диагонали суммы элементов, которые лежат на диагоналях, перпендикулярных к главной. | 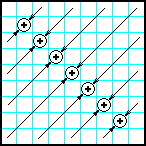
|
| 9 | Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей ЛП, от левого верхнего угла вправо — вниз. Остаток матрицы заполнить нулями. | 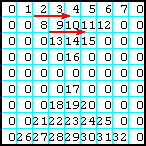
|
| 10 | Заполнить матрицу случайными числами. Отобразить симметрично относительно горизонтальной оси секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей. | 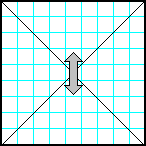
|
| 11 | Заполнить матрицу случайными числами. Развернуть матрицу на 180o. | 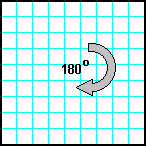
|
| 12 | Заполнить матрицу ЛП, от левого нижнего угла по диагонали: влево — вверх. | 
|
| 13 | Заполнить секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей ЛП, от левого верхнего угла вправо — вниз. Остаток матрицы заполнить нулями. | 
|
| 14 | Заполнить матрицу ЛП, от левого верхнего угла по диагонали: вправо — вверх. | 
|
| 15 | Заполнить матрицу случайными числами. Отобразить главную и побочную диагонали симметрично относительно горизонтальной оси. | 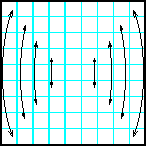
|
| 16 | Заполнить матрицу ЛП, от правого верхнего угла по диагонали: влево — вниз. | 
|
| 17 | Заполнить матрицу случайными числами. Развернуть матрицу на 90o против часовой стрелки. | 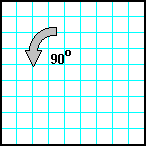
|
| 18 | Заполнить матрицу случайными числами. На побочной диагонали разместить суммы элементов, которые лежат на той же строке и столбце. | 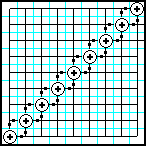
|
| 19 | Заполнить матрицу случайными числами. На главной диагонали разместить суммы элементов, которые лежат на той же строке и том же столбце. | 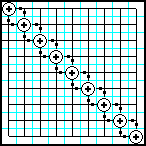
|
| 20 | Заполнить матрицу случайными числами. Отобразить правую половину матрицы на левую зеркально симметрично относительно вертикальной оси. | 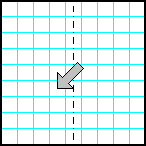
|
| 21 | Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от левого верхнего угла по спирали: вниз — вправо — вверх — влево. | 
|
| 22 | Заполнить матрицу случайными числами. Отобразить левую половину матрицы на правую зеркально симметрично относительно вертикальной оси. | 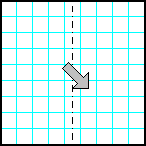
|
| 23 | Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от центра по спирали: вниз — влево — вверх — вправо. | 
|
| 24 | Заполнить матрицу случайными числами. Развернуть матрицу на 90o по часовой стрелке. | 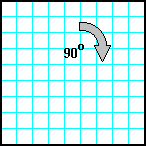
|
| 25 | Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от центра по спирали: вниз — вправо — вверх — влево. | 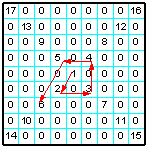
|
| 26 | Заполнить матрицу случайными числами. Разбить матрицу на квадраты размером 3х3. В центре каждого квадрата поместить сумму остальных элементов квадрата. | 
|
| 27 | Заполнить матрицу случайными числами. Отобразить матрицу симметрично относительно главной диагонали | 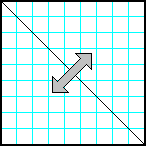
|
| 28 | Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от левого верхнего угла по спирали: вправо — вниз — влево — вверх. | 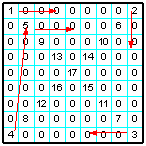
|
| 29 | Заполнить матрицу случайными числами. Отобразить нижнюю половину матрицы на верхнюю зеркально симметрично относительно горизонтальной оси. | 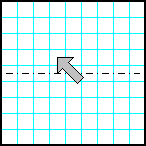
|
| 30 | Заполнить матрицу случайными числами. Разместить на побочной диагонали суммы элементов, которые лежат на диагоналях, перпендикулярных к побочной. | 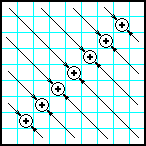
|
| 31 | Заполнить нечетные диагонали, симметричные побочной, с левого верхнего угла заданнимобразом. Остаток матрицы заполнить нулями. | 
|
| 32 | Заполнить главнуюи побочные диагонали матрицы ЛП начинаяс верхнего угла главной диагонали и останавливая заполнение в нижнемуглу побочной диагонали (срединную точку заполнявать один раз, если она есть). Остаток матрицы заполнить нулями. | 
|
| 33 | Заполнить матрицуиз центра, распространяя ЛП вобестороны параллельно строкам и столбцам. | 
|
| 34 | Заполнить матрицу ЛП по диагоналям, симметричным побочной, с левого верхнего угла заданнымобразом — на каждой из диагоналей числа однаковыевдоль нее. | 
|
| 35 | Заполнить матрицу ЛП змейкой, начинаяеес левого верхнего угла матрицы вниз изаполняяее на следующем столбце в обратном направлении. | 
|
| 36 | Заполнить матрицуслучайными числами. Отобразить левые частиглавнойи побочной диагоналей симметрично относительно вертикальной оси. | 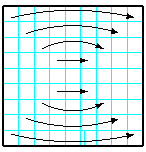
|
| 37 | Заполнить матрицу ЛП змейкой, начинаяеес нижнего правого угла матрицывлево изаполняяее на следующей строке в обратном направлении. | 
|
| 38 | Заполнить матрицуиз центра, распространяя ЛП во обе стороны параллельно главной и побочной диагоналям. | 
|
| 39 | Заполнить матрицуслучайными числами. На срединных строкахи столбцах разместить суммы элементов, лежащихв соответствующихстрокахи столбцах. | 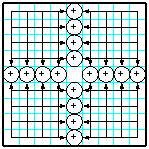
|
| 40 | Заполнить нечетные диагонали, симметричные главной, с правого верхнего угла заданнымобразом. Остаток матрицы заполнить нулями. | 
|
5. Пример решения задачи
| Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями. | 
|
5.1. Разработка алгоритма решения
Если обозначим размерность матрицы как S, номер строкикак L, а номер столбцакак R, и (имея в виду, что реализация алгоритма будет выполнена на языке С) договоримся, что нумерация строк и столбцов будет начинаться с 0, то можно определить, что в строке с номером L ненулевые элементы в верхней частиматрицы лежат на столбцахс номерамиR1=L<R<R2=S–L, ав нижней—R1=S–L–1<R<R2=L. Следовательно, алгоритм может состоять из перебора матрицы строка за строкой с определением для каждого элемента, удовлетворяют ли его индексы вышеприведенным условиям. Если да — элементу присваивается следующее значение из ЛП, если нет — 0.
Но можно несколько упростить алгоритм, обойдя вычисления граничных значений для каждого элемента и необходимости определения, в верхнюю или нижнюю часть матрицы ми попадаем. Обратим внимание на то, что для первой строки (L=0) R1=1, R2=S–2. Для каждой следующей строкиR1 увеличивается на 1, аR2уменьшается на 1. .Когда пересекаем середину матрицы, то направление модификации изменяется на противоположное: теперь для каждой следующей строкиR1уменьшается на 1, аR2 увеличивается на 1. Признаком пересечения середины может быть условиеR1>R2, оно выполняется в момент пересечения. Схема алгоритма показана на рисунке.
Вместе с описанными выше переменнымиR1 и R2, , которые получают начальные значения для первой строки матрицы, ми вводим переменнуюddсначальным значением 1 — это то значение, которое будет модифицироватьR1 и R2 для каждойследующейстроки, ипеременную k— в которой будет значение текущего члена ЛП, начальное значение — 1 (блок 2). Далее организуются вложенные циклы. Во внешнем цикле перебираются строки (блок 3), а во внутреннем — столбцы матрицы (блок 4). В каждой итерации внутреннего цикла номер столбца Rсравнивается с граничными значениями R1, R2 (блоки 5,6). Еслион лежит впределахот R1доR2, то текущему члену матрицы присваивается значенмеk— текущего члена ЛП, а потомkувеличивается на 1 (блок 7). Если нет, тотекущему членуприсваивается значения 0 (блок 8).
После выхода из внутреннего цикла модифицируются граничные значения:R1 увеличиваетсянаdd, аR2 уменьшатся наdd(блок 9). Напомним, чтоначальное значение dd=1. Когда выполняется условие R1>R2(блок 10) присваиваем ddзначение –1, далее модификация границ будет соответствовать правилам для нижней части матрицы.
После выхода из внешнего цикла, который начался в блоке 3, вновь организуются вложенные циклы перебора строк (блок 12) и столбцов (блок 13). В каждой итерации внутреннего цикла выводится значение одного элемента матрицы (блок 14), после выхода из внутреннего цикла начинается новая строка вывода (блок 15).
Дата: 2018-12-21, просмотров: 560.