Цель занятия: выполнить статический расчет второстепенных балок и плит монолитного балочного ребристого перекрытия.
При статическом расчете элементов монолитного ребристого перекрытия вводится условная расчетная схема, у которой опорами главных балок являются колонны и стены, второстепенные балки опираются на главные балки и на стены; в свою очередь балки являются опорами для плиты.
6.1 Определение внутренних усилий в балочной плите.
Плиту можно рассматривать как балочную только при действии на нее равномерно распределенной нагрузки. При статическом расчете плита рассматривается как неразрезная многопролетная балка с расчетным пролетом, равным расстоянию в свету между второстепенными балками, а для крайнего – расстоянию от оси опоры на стене до ближайшей грани ребра (для зданий с неполным каркасом). Расчет ведут для полосы шириной 1м. При количестве пролетов более пяти, расчет выполняют как для пятипролетной балки, т.к. усилия во всех средних пролетах плиты незначительно отличаются от усилия в третьем пролете.
На работу участков плиты, защемленных по четырем сторонам, в местах сопряжения с балками благоприятное влияние оказывает распор. Поэтому для таких плит значения изгибающих моментов в сечениях промежуточных пролетов и опор уменьшаются на 20%.
Расчет необходимо выполнять для двух полос, условно выделенных у торцевой стены и в средней части, чтобы определить внутренние усилия для плит с различными условиями опирания.
| Таблица 6.1 - Расчетные пролеты плиты | |
Крайние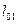 
| Средние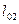 
|
| Расстояние от середины площадки опирания плиты на стену (для зданий с неполным каркасом) до ближайшей к стене грани ребра второстепенной балки | Расстояние в свету между второстепенными балками |
| Таблица 6.2 - Значения внутренних усилий в сечениях плиты | ||||||
| усилие | на первой опоре | в первом (крайнем) пролете | на первой промежуточной опоре | в средних пролетах | на средних опорах | в средних пролетах и на средних опорах, где плиты окаймлены по всему контуру монолитно связанными с ними балками |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| M | - |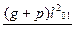 
| 
| 
|
| 
|
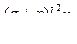
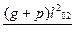
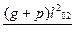
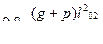
| V |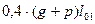 
| - | 
| - | 
| - |
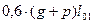
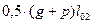
Изгибающий момент положительный в пролете и отрицательный на опорах.
6.2 Определение внутренних усилий в сечениях второстепенной балки.
Расчет второстепенной балки монолитного балочного ребристого перекрытия осуществляется по методу предельного равновесия с учетом перераспределения усилий. Нагрузка на балку передается от плиты с грузовой ширины, равной шагу второстепенных балок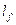 
, также учитывается собственный вес второстепенной балки.
| Таблица 6.3 – Расчетные пролеты второстепенной балки | |
| Крайние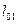
| Средние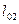
|
| Расстояние от середины площадки опирания балки на стену (для зданий с неполным каркасом) до ближайшей к стене боковой грани главной балки | Расстояние в свету между главными балками |
Длина площадки опирания второстепенной балки определяется прочностью материала стены на местное сжатие.
Поскольку в сечениях второстепенной балки могут действовать изгибающие моменты различных знаков, то их нахождения только для основных пролетных и опорных сечений недостаточно. Необходимо определять положительные и отрицательные моменты для нескольких сечений балки по длине с построением огибающей эпюры. Вычисление изгибающих моментов удобно выполнять в табличной форме с использованием данных ПРИЛОЖЕНИЯ. При этом ординаты огибающей эпюры моментов определяют по формуле: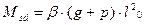 
,
где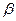 
- коэффициент, определяемый в зависимости от величины соотношения временной и постоянной нагрузок.
Прочность наклонных сечений рассчитывают в трех сечениях: у первой свободной опоры «А» (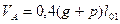 
), у второй (первой промежуточной) опоры «В» (слева - 
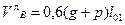; справа - 
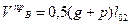). Поперечные силы на промежуточных опорах такие же, как и на второй справа 
.
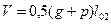Пример 6.
Требуется:
По исходным данным примера 5 и с учетом принятой компоновки определить внутренние усилия в плите и второстепенной балке монолитного ребристого перекрытия.
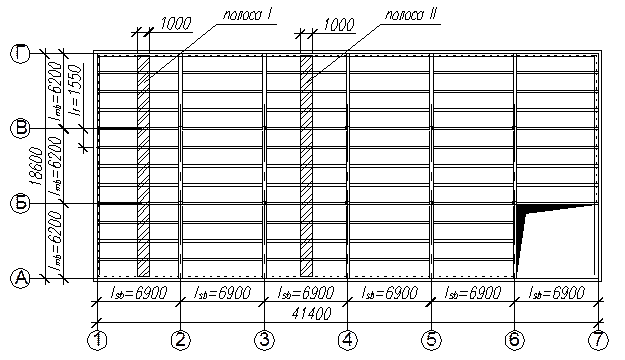
Решение:
I. Определение внутренних усилий в монолитной балочной плите.
Сбор нагрузок на м2 междуэтажного перекрытия представлен в табл.6.4
Таблица 6.4 – Нагрузки на 1м2 монолитного перекрытия
| Вид нагрузки | Нормативная нагрузка, кН/м2 | Частный коэффициент безопасности | Расчетная нагрузка, кН/м2 |
| Постоянная -от собственного веса плиты (d=0,08м, r=25 кН/м3); - от бетонного пола, δ=0,07м, r=20кН/м3 | 2 1,4 | 1,35 1,35 | 2,7 1,89 |
| Итого | 3,4 | 4,59 | |
Временная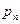 
| 9,0 | 1,5 | 13,5 |
| Всего | 12,4 | 18,09 |
Расчетные пролеты:
- крайние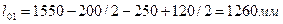 
- средние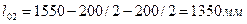 
,
где 250мм – привязка наружных стен;
120мм – длина опирания плиты на наружную стену.
| Таблица 6.5 – Значения внутренних усилий в сечениях плиты | ||||||
| усилие | на первой опоре | в первом (крайнем) пролете | на первой промежуточной опоре | в средних пролетах | на средних опорах | в средних пролетах и на средних опорах, где плиты окаймлены по всему контуру монолитно связанными с ними балками |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Значения внутренних усилий в сечениях плиты для полосы I | ||||||
| M, кНм | - |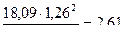 
| 
| 
|
| - |
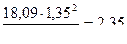
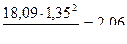
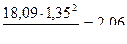
| V, кН | 
| - | 
| - | 
| - |
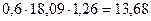
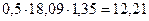
| Значения внутренних усилий в сечениях плиты для полосы II | ||||||
| M, кНм | - |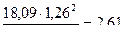
|
| 
| ||
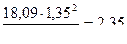
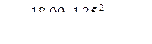
| V, кН |
| - |
| - |
| - |
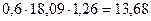
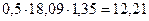
II. Определение внутренних усилий в сечениях второстепенной балки монолитного балочного перекрытия.
Длина площадки опирания второстепенной балки на стену – 250мм, тогда расчетные пролеты:
- крайние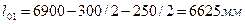 
- средние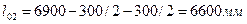 
.
Второстепенная балка работает совместно с прилегающими к ней участками плиты, и ее расчетное сечение будет тавровым с шириной полки равной шагу балок, т.е.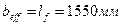 
. Подсчет нагрузок на погонный метр второстепенной балки.
Таблица 6.6 – Нагрузка на 1м.п. второстепенной балки монолитного перекрытия
| Вид нагрузки | Нормативная нагрузка, кН/м | Частный коэффициент безопасности | Расчетная нагрузка, кН/м |
| Постоянная -от собственного веса плиты (d=0,08м, r=25 кН/м3); - от бетонного пола, δ=0,07м, r=20кН/м3 | 0,08х25х1,55=3,1 0,07х20х1,55=2,17 | 1,35 1,35 | 4,19 2,93 |
Итого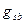 
| 5,27 | 7,12 | |
Временная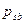 
| 9,0х1,55=13,95 | 1,5 | 21,62 |
| Всего | 19,22 | 28,74 |
При количестве пролетов более 5-ти к расчету принимается пятипролетная схема.
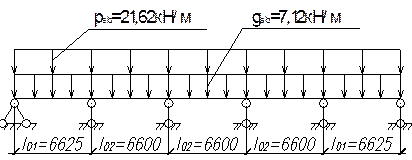
Ординаты огибающей эпюры моментов определяют по формуле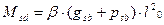 
. Величины коэффициентов 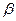определяем в зависимости от величины соотношения 
.
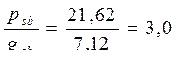Результаты расчета сведены в табл.6.7 и отображены на рис. 6.1.
Таблица 6.7 – Изгибающие моменты второстепенной балки
| № пролёта | № точки | Доля пролёта | b | кНм | М, кНм | ||
| + | - | ММАХ | ММIN | ||||
| I | 1 | 0,2 l01 | 0,065 | 1261,4 | 82,0 | ||
| 2 | 0,4 l01 | 0,090 | 113,5 | ||||
| мах | 0,425 l01 | 0,091 | 114,8 | ||||
| 3 | 0,6 l01 | 0,075 | 94,6 | ||||
| 4 | 0,8 l01 | 0,020 | 25,2 | ||||
| 5 | 1,0 l01 | - | -0,0715 | -90,2 | |||
| II | 6 | 0,2 l01 | 0,018 | -0,035 | 1261,4 | 22,7 | -44,1 |
| 7 | 0,4 l01 | 0,058 | -0,016 | 73,2 | -20,2 | ||
| мах | 0,5 l01 | 0,0625 | -0,015 | 78,8 | -18,9 | ||
| 8 | 0,6 l01 | 0,058 | -0,014 | 73,2 | -17,7 | ||
| 9 | 0,8 l01 | 0,018 | -0,029 | 22,7 | -36,6 | ||
| 10 | 1,0 l01 | - | -0,0625 | -78,8 | |||
| III | 11 | 0,2 l01 | 0,018 | -0,028 | 1261,4 | 22,7 | -35,3 |
| 12 | 0,4 l01 | 0,058 | -0,01 | 73,2 | -12,6 | ||
| мах | 0,5 l01 | 0,0625 | -0,01 | 78,8 | -12,6 | ||
,
Нулевые точки эпюры положительных моментов расположены на расстояниях 0,15 l0 от грани опор:
- в крайнем пролёте: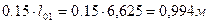 
- в средних пролётах: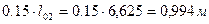 
Положение нулевой точки отрицательных моментов в 1-м пролёте:
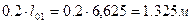
Перерезывающие силы (у граней опор):
- на первой свободной опоре (А): 0,4х28,74х6,625=76,2кН;
- на первой промежуточной опоре (В) слева: 0,6х28,74х6,625=114,2кН;
- на первой промежуточной опоре (В) справа и у остальных опор:
0,5х28,74х6,625=95,2кН.
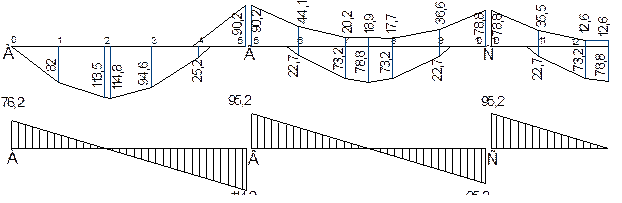
6.1 Эпюра изгибающих моментов (кНм) и поперечных сил (кН)
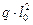Дата: 2018-12-21, просмотров: 207.
