Будем рассматривать аффинные по модулю p размещения m-мерного массива X в общей распределенной памяти. Это такие размещения, при которых элемент массива X(i1,i2,...,im) находится в модуле памяти с номером u = (s1*i1+s2*i2+...+sm*im+s0) mod p, где s0,s1,s2,...sm – константы, зависящие только от массива X.
Если s2 = s3 = ,..., = sm = 0, то размещение многомерного массива X сводится к размещению семейства одномерных массивов (s2, ..., sm – параметры этого семейства).
Если C – некоторая константа, то для множества точек (i1, i2, ..., im) гиперплоскости s1*i1+s2*i2+...+sm*im+s0 = С все элементы массива X(i1,i2,...,im) лежат в одном модуле памяти.
Будем предполагать, что имеется p модулей памяти и будем рассматривать гнездо циклов (16), содержащее два вхождения массивов.
DO 1 I1 = 0, N1
...................................
DO 99 In = 0, Nn
99… = X(a10+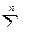 
a1j*Ij,..,am0+ 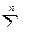amj*Ij) + Y(b10+ 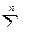b1j*Ij,..,bk0+ 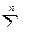bkj*Ij)
Будем рассматривать вопрос о том, когда эти вхождения оказываются в одном и том же модуле памяти.
Теорема 23. Пусть в гнезде циклов (16) есть два вхождения
X(a11*i1+...+a1n*in+a10, a21*i1+...+a2n*in+a20,..., am1*i1+...+amn*in+am0)
и
Y(b11*i1+...+b1n*in+b10, b21*i1+...+b2n*in+b20,..., bk1*i1+...+bkn*in+bk0)
m-мерного массива X и k-мерного массива Y соответственно.
Для того чтобы эти два вхождения были в разных модулях памяти для всех значений счетчиков циклов i1,i2,...,in, необходимо и достаточно, чтобы число
НОД{[(s1*a11 +s2*a21+... sm*am1) – (t1*b11 +t2*b21+... tk*bk1)], ..., [(s1*a1n+s2*a2n+...+ sm*amn) – (t1*b1n+t2*b2n+...+ tk*bkn)], p}
не являлось делителем числа
(s1*a10+s2*a20+...+ sm*am0+s0) – (t1*b10+t2*b20+...+ tk*bk0+ t0)
Доказательство. Если для некоторого вектора счетчиков циклов (i1,i2,...,in) оба вхождения X и Y находятся в одном и том же модуле памяти, то должно выполняться равенство
s1*(a11*i1+...+a1n*in+a10)+s2*(a21*i1+...+a2n*in+a20)+...+ sm*(am1*i1+...+amn*in+am0)+s0 =
t1*(b11*i1+...+b1n*in+b10)+t2*(b21*i1+...+b2n*in+b20)+...+ tk*(bk1*i1+...+bkn*in+bk0) +t0 mod p
Это равносильно существованию решения диофантова уравнения относительно переменных (i0,i1,i2,...,in)
[(s1*a11 +s2*a21+... sm*am1) – (t1*b11 +t2*b21+... tk*bk1)]*i1+...+[(s1*a1n+s2*a2n+...+ sm*amn) – (t1*b1n+t2*b2n+...+ tk*bkn)]*in +
(s1*a10+s2*a20+...+ sm*am0+s0) – (t1*b10+t2*b20+...+ tk*bk0+ t0 ) + p*i0= 0
Условие существования такого решения имеет следующий вид: число
НОД{[(s1*a11 +s2*a21+... sm*am1) – (t1*b11 +t2*b21+... tk*bk1)], ..., [(s1*a1n+s2*a2n+...+ sm*amn) – (t1*b1n+t2*b2n+...+ tk*bkn)], p}
является делителем числа
(s1*a10+s2*a20+...+ sm*am0+s0) – (t1*b10+t2*b20+...+ tk*bk0+ t0)
Взяв отрицание этого условия, получим утверждение теоремы.
Конец доказательства.
Аналогичным образом доказывается следующая
Теорема 24. Пусть в гнезде циклов (16) есть два вхождения m-мерного массива X:
X(a11*i1+...+a1n*in+a10, a21*i1+...+a2n*in+a20,..., am1*i1+...+amn*in+am0)
и
X(b11*i1+...+b1n*in+b10, b21*i1+...+b2n*in+b20,..., bm1*i1+...+bmn*in+bm0).
Для того чтобы эти два вхождения были в разных модулях памяти для всех значений счетчиков циклов i1,i2,...,in, необходимо и достаточно, чтобы число
НОД{[s1*(a11 - b11)+s2*(a21 - b21) + ... sm*(am1 – bk1)], ..., [s1*(a1n - b1n )+ s2*(a2n - b2n) + ... + sm*(amn –bmn)], p}
не являлось делителем числа
s1*(a10 - b10) +s2*(a20 - b20) + ... + sm*(am0 – bm0)
РАСПАРАЛЛЕЛИВАЮЩИЕ/ОПТИМИЗИРУЮЩИЕ ПРЕОБРАЗОВАНИЯ ПРОГРАММ
Автоматическая оптимизация программ – одна из наиболее горячих точек развития науки. Действительно, во всем Мире в каждый момент времени работают миллионы программ. Предположим, что среди них 100 000 программ такие, что пользователи ждут окончания их работы. Предположим, что все компиляторы в Мире станут выдавать код всего лишь на 1% более быстрый, чем прежде. Это означает, что сто тысяч программ за сутки сэкономят около четверти часа. Итого, экономия порядка 24 000 человеко-часов в сутки! А если внедренные оптимизирующие преобразования можно будет переносить на будущие компьютеры, то эффект об их разработки астрономический.
Теория оптимизирующих преобразований программ насчитывает несколько десятилетий. Десятилетиями уже может исчисляться и практика применения этих преобразований в компиляторах, как в нашей стране, так и за рубежом. При этом описываются преобразования, как правило, на примерах высокоуровневых программ. Более всего литература по теории преобразования программ ориентируется на программы языка ФОРТРАН. А в компиляторах используются, в основном, низкоуровневые преобразования. Чаще всего это преобразования ассемблерных текстов в трехадресном внутреннем представлении. Этот дуализм, видимо, связан с тем, что теорию легче писать (и читать!) на языке высокого уровня. А ассемблер – это промежуточный язык, который, с одной стороны, удобен для отображения в него языка высокого уровня, а с другой стороны, для генерации кода. И чем ближе язык по уровню к архитектуре, тем более оптимально можно к архитектуре подогнать программу.
С течением времени накапливаются все новые и новые преобразования программ. В старых компиляторах блок оптимизации занимал сравнительно небольшую долю всего программного кода, по сравнению с парсером и генератором кода. Теперь блок оптимизации может занимать объем превосходящий остальную часть компилятора. По уровню использованного интеллекта блок оптимизации никак не уступает остальной части компилятора, особенно в последние годы при появлении автоматически распараллеливающих преобразований. Это приводит к проблеме понижения стоимости компиляторов при повышении их сложности.
Проблема удешевления компиляторов становится все более острой с расширением разнообразия вычислительных архитектур. Это разнообразие диктуется ростом потребности в высокопроизводительных вычислениях для различных прикладных задач в таких областях, как обработка сигналов, искусственный интеллект, научные исследования, управление большими базами данных, управление сложными объектами и других. При этом различные задачи могут предъявлять различные требования к архитектуре используемого компьютера: целые или вещественные числа, длина разрядной сетки, синхронность или асинхронность, конвейерность и т.д. Разнообразие малосерийных высокопроизводительных вычислительных архитектур реализуется в значительной степени на основе ПЛИС – программируемых логических интегральных схемах, которые в последние годы набирают все большую популярность.
Очевидным способом удешевления компиляторов является их переносимость, хотя бы частичная. В частности, переносимость блока оптимизации. Чем выше уровень внутреннего представления, на котором оптимизирующие преобразования реализованы, тем легче они переносимы. Разумеется, речь может идти только о машинно-независимых оптимизациях. Машинно-ориентированные преобразования могут быть дописаны к каждому конкретному компьютеру отдельно. Чем больше преобразований можно поднять на высокий уровень, тем легче можно будет создавать семейство компиляторов на их основе. Например, по такому пути пошли разработчики распараллеливающих компиляторов фирмы Portland Group, взяв за основу высокоуровневое внутреннее представление SUIF. Высокоуровневое внутреннее представление для преобразований программ лежит и в основе ОРС – Открытой распараллеливающей системы, которая разрабатывается в Южном федеральном университете www.ops.rsu.ru.
6.1 Программные зависимости и базовые преобразования
Управляющий граф программы
Управляющий граф [42], [51], [52] – это одна из основ преобразования программ. Даже если в описании преобразования управляющий граф не упоминается, то он, как правило, подразумевается. В явном или неявном виде управляющий граф присутствует во внутренних представлениях оптимизирующих/распараллеливающих компиляторов.
Перед описанием преобразований и управляющего графа программ следует определиться, о каких программах будет идти речь.
Программы – это предложения языков программирования. В научной литературе высокоуровневые преобразования более всего описаны для программ языка ФОРТРАН. Встречаются также описания преобразований для языков Си и Паскаль, реже – для других высокоуровневых языков. Абстрагируемся от этих конкретных языков, чтобы преобразования носили как можно более общий характер. Программу будем рассматривать, как последовательность единиц языка. Будем считать, что рассматриваемые программы содержат следующие операторы:
операторы присваивания,
циклы со счетчиком (параметром, считающим итерации),
блочные условные операторы,
операторы безусловного перехода на метку GOTO,
пустые операторы,
Блочные операторы (операторные скобки),
Операторы вызова подпрограммы (процедуры или функции).
Предполагается, что в рассматриваемом языке программирования допускается конкатенация операторов.
Данные описываются только константами, скалярными переменными и массивами.
Программы могут исполняться, изменяя этим самым состояние памяти компьютера.
Исполнение программы состоит в чтении единиц языка (операторов, линейных участков), сопоставлении переменных, входящих в выражения с их значениями и изменении значений переменных (соответствующих им состояний ячеек памяти). Последовательность чтения единиц языка определяется семантикой языка программирования. Если две единицы языка могут прочитаться при некотором исполнении программы одна после другой, то говорят, что они связаны передачей управления.
Фрагмент программы – это такая часть подряд идущих по тексту операторов, заключение в скобки которой приводит к программе, эквивалентной исходной.
Базовый блок или линейный участок программы – это фрагмент, состоящий только из операторов присваивания.
В частности, у программы выделяются входные данные и выходные данные. Две программы считаются эквивалентными, если при одних и тех же входных данных в результате исполнения выходные данные у этих программ тоже совпадают.
Вершины управляющего графа – это некоторые элементы языка программирования (в научной литературе чаще всего операторы или линейные участки), а дуги – это передачи управления.
Отметим, что ранее в литературе в качестве вершин управляющего графа предполагалось использовать только операторы программы. Такой подход вполне удобен для программ языка ФОРТРАН, но уже не удобен для языка Паскаль, в котором циклу с постусловием «repeat-until» неудобно сопоставлять одну вершину (вместо «repeat» или вместо «until»?). Если вершины управляющего графа – операторы, то управляющий граф, соответствующий линейному участку имеет вид простого пути. Поэтому такие фрагменты программы и называются «линейными участками». Иногда линейные участки рассматривают в качестве вершин управляющего графа, чтобы сократить размеры графа, сохраняя его топологию.
Если операторы программы связаны конкатенацией, то передача управления между ними происходит в порядке следования этих операторов. Условный оператор и оператор цикла имеют по две передачи управления.
В языках программирования встречаются сложные операторы, которые определяются через другие операторы. Обычно, такие операторы имеют вид
<сложный оператор> ::= term1 statement1 term2 statement2 … termn statementn termn+1
Здесь term1 , term2 , … termn , termn+1 – некоторые зарезервированные слова языка, statement1 , statement2 , … statementn – операторы или выражения. Такой вид имеют операторы цикла, условные операторы, блочный оператор, оператор case в языке Паскаль, оператор switch в языке Си.
Пусть G ориентированный граф, вершинами которого являются единицы языка term1 , statement1 , term2 , statement2 ,…, termn , statement , termn+1 . Пусть этот граф имеет единственный источник и единственный сток term1 и termn+1 соответственно. Дуги этого графа будем считать передачами управления в сложном операторе.
Следует отметить, что при внешней схожести операторов case в языке Паскаль и switch в языке Си, передачи управления у них организованы по разному. Вершины, как бы одинаковые, а дуги связывают эти вершины по разному. Графы передач управления этих операторов не изоморфны.
Приведенное выше аксиоматическое определение передач управления в сложных операторах – элемент семантики этих операторов.
При преобразованиях программ следует контролировать сохранение синтаксической и семантической корректности.
Пример 27. Если в программе языка ФОРТРАН поменять местами заголовок цикла и последний оператор тела цикла, то результирующая программа будет содержать нарушения синтаксиса языка. Следует отметить, что от таких ошибок компиляторы, как правило, застрахованы, поскольку преобразования в них проводятся не над текстом, а над специальным внутренним представлением.
Конец примера.
Пример 28. Если скопировать фрагмент программы, содержащий оператор с меткой, то в результирующем фрагменте получится два оператора с одинаковой меткой, что нарушает семантическую корректность. Копирования операторов встречаются в таких преобразованиях циклов, как развертка, раскрутка, гнездование, расщепление.
Конец примера.
Причины такой некорректности часто связаны с пренебрежением к управляющему графу программы при проведении преобразований.
Вход фрагмента программы – это передача управления, начало которой находится вне рассматриваемого фрагмента, а конец – внутри фрагмента. Аналогично определяется выход фрагмента.
Пример 29. В данном примере у фрагмента, состоящего из одного оператора 999, по крайней мере, два входа: один от предыдущего присваивания, а другой – от условного оператора.
IF BOOLEXPR THEN
A = 1
999 X = 1
Конец примера.
Иногда перед выполнением преобразования рассматриваемый фрагмент необходимо заключать в операторные скоби. В работе [121] преобразуемые циклы приводятся к такому виду, в котором перед заголовком и после тела ставятся пустые операторы с метками, которые перехватывают передачи управления, входящие в рассматриваемый цикл и выходящие из него.
Пример 30. В этом примере все операторы информационно независимы. Управление передается от каждого предыдущего оператора к последующему. Но операторы 3 и 4 можно менять местами, а операторы 1 и 2 – нельзя. Заметим, что перестановка операторов 1 и 2 приводит к программе синтаксически и семантически корректной, но не эквивалентной исходной. По этой причине иногда приходиться оговаривать, какие именно операторы входят в рассматриваемый фрагмент.
1 GOTO 2
2 X = 1
3 Y = 2
4 Z = 3
Конец примера.
Строгое определение корректности преобразования программ обсуждается в [43]. В данной работе исследуются эквивалентность или эффективность преобразований программ. Корректность преобразований если не оговаривается, то подразумевается.
При автоматических преобразованиях программ в оптимизирующих компиляторах программы, как правило, находятся в древовидных внутренних представлениях. И преобразования проводятся во внутреннем представлении и представляют собой преобразования деревьев. Этим самым устраняются некоторые некорректности, которые возможны при преобразованиях текста. Например, невозможно переставить местами тело цикла и заголовок цикла, поскольку заголовок цикла – это корень куста, на котором тело цикла находится, а переставлять можно только целые кусты.
Дата: 2018-12-21, просмотров: 463.
