В ПОСЛЕДОВАТЕЛЬНОМ РЕЗОНАНСНОМ КОНТУРЕ
Цель работы
Экспериментально исследовать переходные процессы в последовательном колебательном контуре RLC при воздействии прямоугольного импульса.
2. Задание на самостоятельную подготовку к работе
2.1. Изучите методы анализа переходных процессов в цепях, содержащих R, L, C и особенности определения реакций в этих цепях при воздействии прямоугольного импульса.
2.2. В соответствии со своим номером варианта выпишите из табл. 3.1 значения параметров RLC-контура (рис. 3.1) и рассчитайте значение Скр, при котором возникает критический режим, используя соотношение Rкр= 2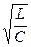 
. Полученное значение Скр занесите в табл.3.2.
2.3. Определите, какой режим будет при C1 и С2. Качественно постройте графики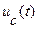 
при С1 и С2 при воздействии прямоугольного импульса tи=200 мкс.
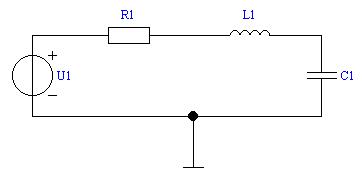
Рис. 3.1
2.4. Рассчитайте С3 так, чтобы период свободных колебаний Tс=50 мкс:
Tс =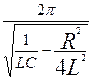 
.
2.5. Рассчитайте и запишите в табл. 3.2 и 3.3 следующие величины:
а) добротность контура при разных значениях емкости С1, С2, С3, Скр:
;
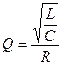б) значение периода свободных колебаний Tс при С=С2:
Tс =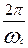 
=
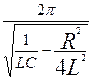
в) корни характеристического уравнения p1 и p2, величины декремента затухания Δ и логарифмического декремента затуханияּαTс при С=С2 и С=С3:
Р1,2=-α±jωс, α=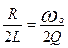 
; 
; 
; 
;
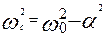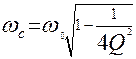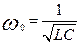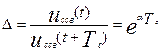; αTс=lnΔ
Таблица 3.1
Значения параметров RLC-контура
|
Вариант |
Лаборатория 1 (631)
|
Лаборатория 2 (620)
| ||||||
| R, Ом | L, мГн | C1, мкФ | C2, мкФ | R, Ом | L, мГн | C1, мкФ | C2, мкФ | |
| 1 | 144 | 3,14 | 0,75 | 0,05 | 144 | 4,64 | 0,95 | 0,045 |
| 2 | 234 | 6,364 | 0,7 | 0,025 | 234 | 6,28 | 0,72 | 0,028 |
| 3 | 146 | 4,46 | 0,95 | 0,056 | 146 | 4,8 | 0,95 | 0,05 |
| 4 | 230 | 6,878 | 0,65 | 0,04 | 230 | 6,9 | 0,75 | 0,04 |
| 5 | 228 | 7,88 | 0,85 | 0,032 | 228 | 6,86 | 0,82 | 0,038 |
| 6 | 228 | 4,677 | 0,55 | 0,026 | 228 | 5,08 | 0,65 | 0,028 |
| 7 | 209 | 4,458 | 0,75 | 0,03 | 209 | 4,654 | 0,75 | 0,035 |
| 8 | 212 | 4,510 | 0,69 | 0,052 | 230 | 5,24 | 0,85 | 0,05 |
| 9 | 234 | 4,774 | 0,62 | 0,025 | 234 | 4,54 | 0,65 | 0,028 |
| 10 | 231 | 6,994 | 0,72 | 0,035 | 231 | 6,42 | 0,85 | 0,04 |
| 11 | 116 | 2,21 | 0,85 | 0,055 | 116 | 1,8 | 0,84 | 0,06 |
| 12 | 212 | 4,51 | 0,85 | 0,027 | 231 | 5,24 | 0,88 | 0,035 |
2.6. Рассчитайте и занесите в таблицу 3.3 корни характеристического уравнения p1 и p2 при С=С1 и С= Скр, используя формулу
Р1,2=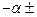 
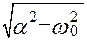
2.7. Покажите на комплексной плоскости расположение корней характеристического уравнения при различных значениях емкости С1, Скр, С2, С3 с указанием соответствующей величины добротности Q.
Задание для экспериментальной работы
3.1. Для экспериментального исследования переходного процесса в последовательном колебательном контуре соберите цепь (рис. 3.2).
 |
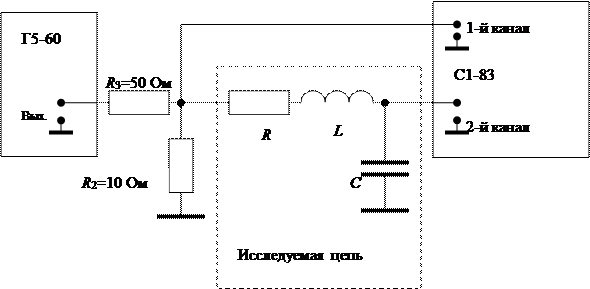Рис. 3.2
3.2. Подготовьте к работе генератор Г5-60 и осциллограф С1-83. Установите на Г5-60
напряжение 1 В, длительность импульсов tи =200 мкс, период их следования Т=660 мкс.
На 1-й канал осциллографа подайте напряжение с сопротивления R2, а на второй канал – с емкости C. Получите на экране осциллографа с 1-го канала изображение одного импульса размером 4 х 4 дел. Получите на экране осциллографа со 2-го канала изображение напряжения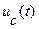 
, соответствующее импульсу 1-го канала. При всех дальнейших измерениях ручки «время/дел» и «V/дел» не трогайте.
3.3. Установите С=С3. Снимите осциллограмму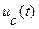 
. Нанесите на осциллограмме точки на оси абсцисс, соответствующие началу импульса, его окончание, измерьте период свободных колебаний Tс, ucсв(t) и ucсв(t + Tc), вычислите их отношение 
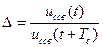, логарифмический декремент затухания αTс=lnΔ, Р1, Р2, результаты эксперимента запишите в табл. 3.2.
3.4. Повторите эксперимент для емкости С=С2. Сделайте вывод о зависимости периода свободных колебаний и логарифмического декремента от величины емкости контура.
3.5. Установите емкость С=С1 и снимите соответствующую осциллограмму.
Таблица 3.2
Результаты расчета и анализа на ПК
|
Предвари- тельный расчет | C, мкс | Q | Tс, мкс |
Δ=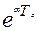 
| αTс |
Р1,2= -α±jωс, 1/с | |
| С2 |
| ||||||
| С3 |
| ||||||
|
Результаты экспери-мента |
| Измеряется по графикам | Вычисляется по данным измерений
| ||||
| Tс |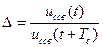
| αTс=ln Δ |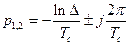 
| ||||
|
С2
|
| ||||||
|
C3 |
| ||||||
Таблица 3.3
Результаты расчета Q, р1 и р2
| C,мкФ | Q |
Р1=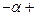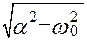 
|
Р2=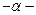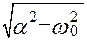 
|
| С1 задано | |||
| Скр |
Указания защите
4.1. Отчет должен содержать:
- схему исследуемой цепи;
-графики напряжений на элементах R, L, C при разных значениях С. На графиках указать, какому режиму колебаний они соответствуют: апериодическому, критическому или колебательному;
-табл. 3.2 и 3.3;
- на комплексной плоскости показать расположение корней характеристического уравнения, рассчитанных по пп.2.5 и 2.6;
- выводы о влиянии величины емкости на добротность контура, период собственных колебаний, декремент затухания и длительность переходного процесса
Контрольные вопросы
1. Какой режим будет в последовательном RLС-контуре при R= 2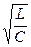 
=Rкр, R > Rкр,
R < Rкр?
2. Что следует понимать под начальными условиями для контура RLC?
3. Какие режимы собственных колебаний возможны в последовательном RLC-контуре?
5. Какие корни характеристического выражения соответствуют каждому из режимов?
6. Какой физический смысл имеют вещественная и мнимая составляющие корней?
7. Как должны измениться потери в цепи, чтобы критический режим перешел в апериодический? в колебательный?
8. Какой вид будет иметь свободная составляющая ucсв(t), если корни характеристического уравнения отрицательные вещественные числа? Комплексно-сопряженные числа? Кратные корни?
8. Может ли частота свободных колебаний ωсв в контуре RLС быть выше (равна, ниже) резонансной частоты ωо этого же контура?
Лабораторная работа 4
ПРЕОБРАЗОВАНИЕ СПЕКТРА КОЛЕБАНИЙ
Дата: 2018-12-21, просмотров: 365.
