1) 
; 
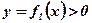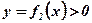при 
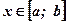(Рис. 1.);
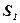- площадь кр. тр., ограниченной функцией 
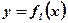при 
: 
;
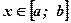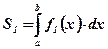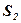- площадь кр. тр., ограниченной функцией 
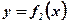при :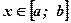 
;
.
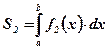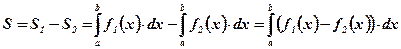2) 
; 
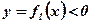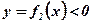при 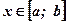(Рис. 2.);
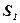- площадь фигуры, ограниченной функцией 
при : 
;
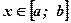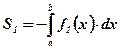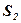- площадь фигуры, ограниченной функцией 
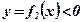при :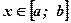 
;
.
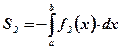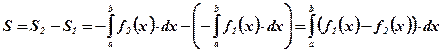3) ; 
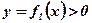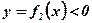при 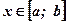(Рис. 3.);
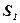- площадь кр. тр., ограниченной функцие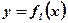й при :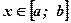 
;
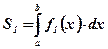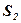- площадь фигуры, ограниченной криво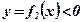й при :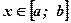 
;
.
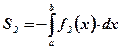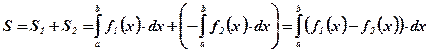Вывод: Площадь фигуры, ограниченной функциям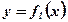и 
и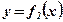 
, удовлетворяющими условию 
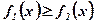при рассматриваемых значениях аргумента 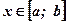, вычисляется по формуле 
.
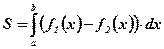Пример: Вычислить площадь фигуры, ограниченной функциям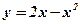и 
и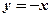 
.
Решение:
; 
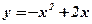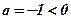- ветви направлены вниз;
; 
; 
; 
;
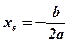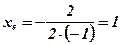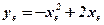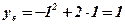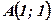- вершина параболы;
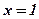- ось симметрии параболы;
| х | 1 | 2 | 3 |
| у | 1 | 0 | -3 |
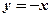
| х | 0 | 3 |
| у | 0 | -3 |
Фигура не является криволинейной трапецией, так как не ограничена осью абсцисс. Площадь фигуры, ограниченной функциям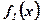и 
и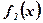 
, удовлетворяющими условию 
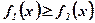при рассматриваемых значениях аргумента 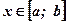, вычисляется по формуле 
, 
; 
.
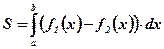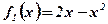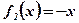Концы интервала, на котором построена данная фигура, являются абсциссами точек пересечения параболы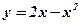 
и прямой .
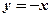Решим способом подстановки систему уравнений:
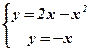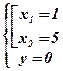Û 
Û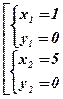 
; 
; 
; 
.
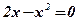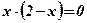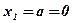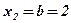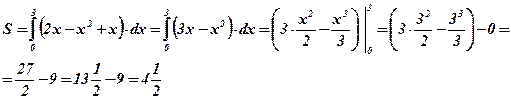
Ответ: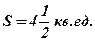 
Замечание:
- Если плоская фигура имеет «сложную» форму, то прямыми, параллельными оси ординат, её следует разбить на части так, чтобы можно было применить уже известные формулы.
- Если фигура расположена симметрично относительно оси ординат или начала координат, то можно упростить вычисления, определив половину площади и затем удвоив результат.
Упражнения:
- Вычислить площадь фигуры, заключённой между параболой
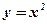и прямой 
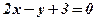. - Вычислить площадь фигуры, ограниченной функциями:
, 
, 
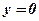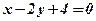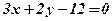. - Вычислить площадь фигуры, ограниченной функциями:
, 
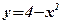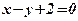. - Вычислить площадь фигуры, ограниченной функциями:
, 
, 
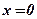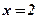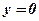, . - Вычислить площадь фигуры, ограниченной функциями:
, 
, 
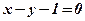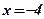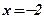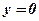, . - Вычислить площадь фигуры, ограниченной функциями:
, , 
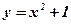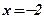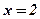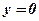, . - Вычислить площадь фигуры, ограниченной функциями:
, 
, 
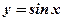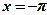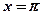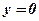, . - Вычислить площадь фигуры, ограниченной функциями:
, 
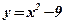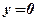. - Вычислить площадь фигуры, ограниченной функциями:
, 
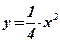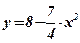. - Вычислить площадь фигуры, ограниченной функциями:
, 
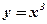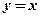. - Вычислить площадь фигуры, ограниченной функциями:
, 
.
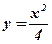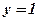10. Контрольные вопросы по теме «Интегральное исчисление функции одной переменной»
1. Дать определение первообразной для заданной функции.
2. Дать определение неопределенного интеграла от заданной функции.
3. Сформулировать свойства неопределенного интеграла от заданной функции.
4. Перечислить основные формулы интегрирования (табличные интегралы).
5. Составить план вычисления неопределенного интеграла от заданной функции способом подстановки.
6. Дать определение определенного интеграла от заданной функции.
7. Сформулировать свойства определенного интеграла от заданной функции.
8. Составить план вычисления определенного интеграла от заданной функции способом подстановки.
9. Дать определение криволинейной трапеции.
- Как вычислить площадь фигуры, не являющейся криволинейной трапецией?
Дата: 2018-12-21, просмотров: 243.
