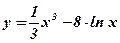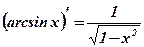 ; ;
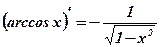 ; ;
| 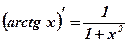 ; ;
 . .
|
Упражнения: Вычислить производные функций:
1. 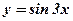 2.
2. 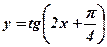 3.
3. 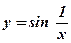 4.
4. 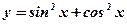
| 5. 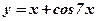 6.
6. 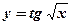 7.
7. 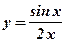 8.
8. 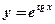 9.
9. 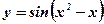
|
10. 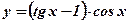 11.
11. 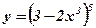 12.
12. 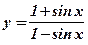 13.
13. 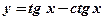
|
11. 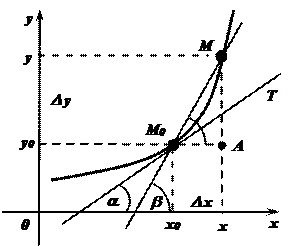 Геометрический смысл производной функции
Геометрический смысл производной функции
Рассмотрим функцию 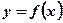 .
.
На графике функции 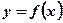 возьмем фиксированную точку
возьмем фиксированную точку  и произвольную точку
и произвольную точку 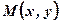 . Проведем секущую
. Проведем секущую 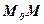 . Если точку М неограниченно приближать к точке М0 по графику функции
. Если точку М неограниченно приближать к точке М0 по графику функции 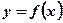 , то секущая М0М будет занимать различные положения и при совпадении точки М с точкой М0 секущая займет предельное положение М0Т, тогда прямая М0Т будет касательной к графику функции в точке М0.
, то секущая М0М будет занимать различные положения и при совпадении точки М с точкой М0 секущая займет предельное положение М0Т, тогда прямая М0Т будет касательной к графику функции в точке М0.
Определение: Касательной к графику функции 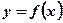 в точке М0 называется предельное положение М0Т секущей
в точке М0 называется предельное положение М0Т секущей 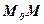 при стремлении точки М по графику к точке М0 .
при стремлении точки М по графику к точке М0 .
b - угол наклона секущей М0М к положительному направлению оси абсцисс.
a - угол наклона касательной М0Т к положительному направлению оси абсцисс.
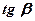 - угловой коэффициент секущей М0М.
- угловой коэффициент секущей М0М.
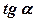 - угловой коэффициент касательной М0Т.
- угловой коэффициент касательной М0Т.
Рассмотрим прямоугольный треугольник М0МА ( 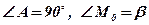 ). Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему:
). Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему: 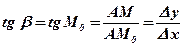
 , то есть
, то есть 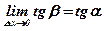 . А, значит,
. А, значит, 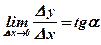 .
.
Определим производную функции 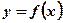 в точке х0:
в точке х0: 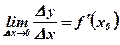 .
.
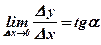 ,
, 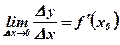 , следовательно,
, следовательно, 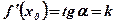 .
.
Вывод: Геометрический смысл производной функции состоит в том, что производная функции 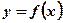 при
при 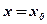 равна угловому коэффициенту касательной, проведенной к графику функции в точке с абсциссой
равна угловому коэффициенту касательной, проведенной к графику функции в точке с абсциссой 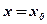 .
.
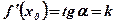
Пример:
1. Найти угловой коэффициент касательной, проведенной к графику функции 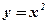 в точках
в точках 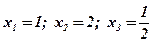 .
.
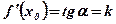 ;
; 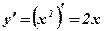 ;
; 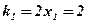 ;
; 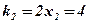 ;
; 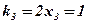 ;
; 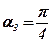 .
.
Ответ: 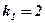 ;
; 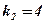 ;
; 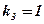 .
.
2. Найти угол наклона касательной, проведенной к графику функции 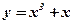 в точке с абсциссой
в точке с абсциссой 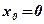 .
.
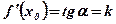 ;
; 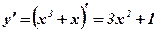 ;
; 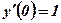 ;
; 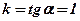 ;
; 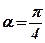 .
.
Ответ: 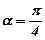 .
.
Упражнения:
1. Какой угол образует с осью Ох касательная к кривой 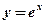 в точке
в точке 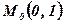 ?
?
2. Найти координаты точки, в которой касательная к параболе 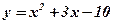 образует угол в 135º с осью Ох.
образует угол в 135º с осью Ох.
3. В какой точке касательная к кривой 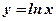 наклонена к оси Ох под углом
наклонена к оси Ох под углом 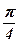 ?
?
4. В какой точке касательная к параболе 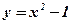 параллельна прямой
параллельна прямой 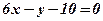 ; перпендикулярна прямой
; перпендикулярна прямой 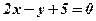 ?
?
5. Определить, в какой точке касательная к параболе 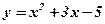 параллельна прямой
параллельна прямой 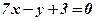 .
.
6. Определить, в какой точке касательная к параболе 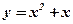 перпендикулярна прямой
перпендикулярна прямой 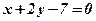 .
.
12. Признаки постоянства, возрастания, убывания функции
Теорема:
1. Если функция 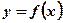 на
на 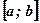 имеет положительную производную, то функция на этом отрезке возрастает.
имеет положительную производную, то функция на этом отрезке возрастает.
2. Если функция 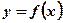 на
на 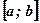 имеет отрицательную производную, то функция на этом отрезке убывает.
имеет отрицательную производную, то функция на этом отрезке убывает.
3. Если функция 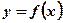 на
на 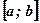 имеет равную нулю производную, то функция на этом отрезке постоянна.
имеет равную нулю производную, то функция на этом отрезке постоянна.
Пример: Определить интервалы возрастания и убывания функции 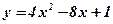 .
.
1. Найдем область определения функции 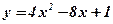 :
: 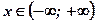 .
.
2. Вычислим производную функции: 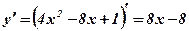 .
.
3. Определим значения аргумента х, при которых производная функции равна нулю: 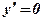 ;
; 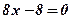 ;
; 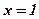 .
.
4. Определим знак производной в интервалах, на которые область определения разбивается значением аргумента 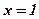 , и характер монотонности функции в этих интервалах:
, и характер монотонности функции в этих интервалах:
| х | 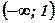
| 1 | 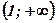
|
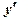
| - | 0 | + |
| у | ↓ | ↑ |
Ответ: 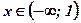 у - убывает;
у - убывает; 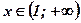 у - возрастает.
у - возрастает.
Пример: Исследовать на монотонность функцию 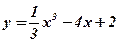 .
.
1. Найдем область определения функции 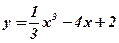 :
: 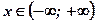 .
.
2. Вычислим производную функции: 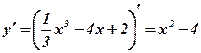 .
.
3. Определим значения аргумента х, при которых производная функции равна нулю: 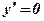 ;
; 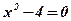 ;
; 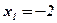 ;
; 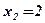 .
.
4. Определим знак производной в интервалах, на которые область определения разбивается значениями аргумента 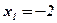 ;
; 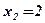 , и характер монотонности функции в этих интервалах:
, и характер монотонности функции в этих интервалах:
| х | 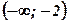
| - 2 | 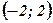
| 2 | 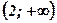
|
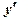
| + | 0 | - | 0 | + |
| у | ↑ | ↓ | ↑ |
Ответ: 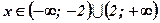 у - возрастает;
у - возрастает; 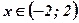 у - убывает.
у - убывает.
Упражнения: Исследовать на монотонность функции:
1. 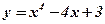 ;
2. ;
2. 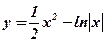 ;
3. ;
3. 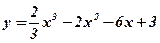
| 4. 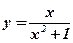 ;
5. ;
5.  ;
6. ;
6. 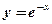 ; ;
| 7. 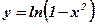 ;
8. ;
8. 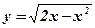 ;
9. ;
9. 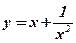 . .
|
13. Экстремумы функции. Исследование функции на экстремум
Рассматривая поведение функции 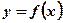 на интервале
на интервале  , обратим внимание на то, что при некоторых значениях аргумента х1, х2, х3 функция принимает либо наибольшее, либо наименьшее значения по сравнению с ее значениями слева и справа от этих значений аргумента. Для пояснения этой особенности функции введем понятия максимума и минимума функции.
, обратим внимание на то, что при некоторых значениях аргумента х1, х2, х3 функция принимает либо наибольшее, либо наименьшее значения по сравнению с ее значениями слева и справа от этих значений аргумента. Для пояснения этой особенности функции введем понятия максимума и минимума функции.

Определение: Значение аргумента х0 называется точкой максимума функции 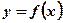 , если для всех значений аргумента х в окрестности х0 выполняется неравенство
, если для всех значений аргумента х в окрестности х0 выполняется неравенство 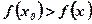 . Рис. 1.
. Рис. 1.
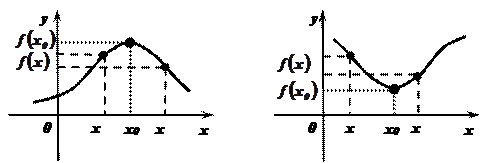 Определение: Значение аргумента х0 называется точкой минимума функции
Определение: Значение аргумента х0 называется точкой минимума функции 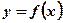 , если для всех значений аргумента х в окрестности х0 выполняется неравенство
, если для всех значений аргумента х в окрестности х0 выполняется неравенство 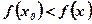 . Рис. 2.
. Рис. 2.
Рис. 1. Рис. 2.
Замечание: Точки максимума и минимума функции называются точками экстремума (extremum – крайний), а значения функции в этих точках – экстремальными (максимальными и минимальными).
Установим необходимое условие существования экстремума.
Теорема Ферма: Если внутренняя точка х0 из области определения непрерывной функции 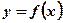 является точкой экстремума и в этой точке существует производная, то она равна нулю.
является точкой экстремума и в этой точке существует производная, то она равна нулю.
Замечание: Однако равенство нулю производной функции в точке х0 еще не дает права утверждать, что х0 – точка экстремума функции.
Пример:
- Функция
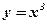 имеет производную
имеет производную 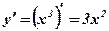 , которая обращается в нуль при х = 0. Но в этой точке функция
, которая обращается в нуль при х = 0. Но в этой точке функция 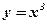 (кубическая парабола) экстремума не имеет.
(кубическая парабола) экстремума не имеет. - Функция
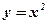 имеет производную
имеет производную 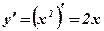 , которая обращается в нуль при х = 0. В этой точке функция
, которая обращается в нуль при х = 0. В этой точке функция 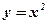 (парабола) имеет минимум.
(парабола) имеет минимум.
Определение: Значения аргумента х, при которых производная функции равна нулю или не существует, называются критическими точками этой функции.
Чтобы определить, имеет ли функция экстремум в данной точке, необходимо воспользоваться достаточными условиями существования экстремума.
Теорема: Значение аргумента х0 является точкой экстремума функции 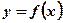 , если производная
, если производная 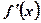 , равная нулю в точке х0, при переходе через х0 меняет знак. При перемене знака с «+» на «–» точка х0 является точкой максимума. При перемене знака с «–» на «+» точка х0 является точкой минимума. Если же производная
, равная нулю в точке х0, при переходе через х0 меняет знак. При перемене знака с «+» на «–» точка х0 является точкой максимума. При перемене знака с «–» на «+» точка х0 является точкой минимума. Если же производная 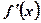 при переходе через х0 не меняет знака, то х0 не является точкой экстремума.
при переходе через х0 не меняет знака, то х0 не является точкой экстремума.
План исследования функции на монотонность и существование точек экстремума
1. Найти область определения функции.
2. Вычислить производную функции.
3. Найти критические точки функции, приравняв производную функции к нулю и решив полученное уравнение.
4. Определить знак производной функции слева и справа от критических точек.
5. Определить характер монотонности функции в полученных интервалах области определения функции и экстремумы функции, если они есть.
6. Вычислить значения функции в точках экстремума.
Пример: Исследовать на экстремум функцию 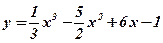 .
.
1. Найдем область определения функции 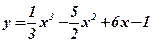 :
: 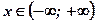 .
.
2. Вычислим производную функции: 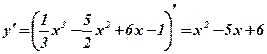 .
.
3. Найдем критические точки функции, то есть значения аргумента х, при которых производная функции равна нулю: 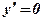 ;
; 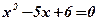 ;
; 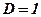 ;
; 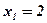 ;
; 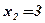 .
.
4. Определим знак производной слева и справа от критических точек 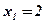 ;
; 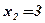 , и характер монотонности функции в полученных интервалах:
, и характер монотонности функции в полученных интервалах:
| х | 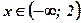
| 2 | 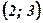
| 3 | 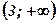
|
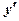
| + | 0 | - | 0 | + |
| у | ↑ | max | ↓ | min | ↑ |
5. Определим точки экстремума функции и экстремальные значения функции:
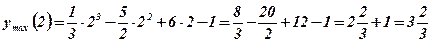 .
.
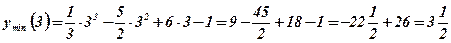 .
.
Ответ: 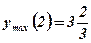 ;
; 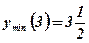 .
.
Упражнения: Исследовать на монотонность и существование точек экстремума функции:
|
|
|
14. Наибольшее и наименьшее значения функции на промежутке
Замечание:
- Точки максимума и минимума функции называют локальными экстремумами функции, так как речь идет об экстремальных значениях функции в окрестностях некоторых точек.
- Наибольшее и наименьшее значения функции на отрезке называют глобальными экстремумами функции.
Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции.
Теорема Вейерштрасса: Непрерывная на отрезке 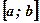 функция
функция  принимает на этом отрезке наибольшее и наименьшее значения.
принимает на этом отрезке наибольшее и наименьшее значения.
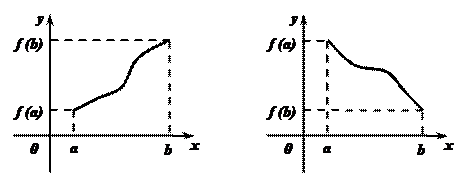 Для случая, когда функция
Для случая, когда функция  не только непрерывна на отрезке
не только непрерывна на отрезке  , но имеет на этом отрезке конечное число критических точек, укажем правило отыскания наибольшего и наименьшего значений функции
, но имеет на этом отрезке конечное число критических точек, укажем правило отыскания наибольшего и наименьшего значений функции 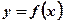 . Предположим, сначала, что
. Предположим, сначала, что 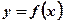 не имеет на отрезке
не имеет на отрезке 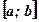 критических точек. Тогда она возрастает (Рис.1.) или убывает (Рис.2.) на этом отрезке, и, значит, наибольшее и наименьшее значения функции
критических точек. Тогда она возрастает (Рис.1.) или убывает (Рис.2.) на этом отрезке, и, значит, наибольшее и наименьшее значения функции  на отрезке
на отрезке 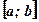 - это значения в концах a и b.
- это значения в концах a и b.
Рис.1. Рис. 2.
Пусть теперь функция 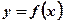 имеет на отрезке
имеет на отрезке 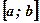 конечное число критических точек. Эти точки разбивают отрезок
конечное число критических точек. Эти точки разбивают отрезок 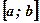 на конечное число отрезков, внутри которых критических точек нет. Поэтому наибольшее и наименьшее значения функции
на конечное число отрезков, внутри которых критических точек нет. Поэтому наибольшее и наименьшее значения функции 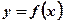 на таких отрезках принимаются в их концах, то есть в критических точках функции или в точках а и b.
на таких отрезках принимаются в их концах, то есть в критических точках функции или в точках а и b.
Вывод: Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Пример: Найти наибольшее и наименьшее значения функции 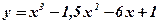 на отрезке
на отрезке 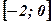 .
.
1) 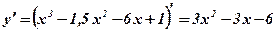 .
.
2) 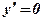 ;
; 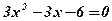 ;
; 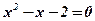 ;
; 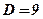 ;
;
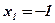 - критическая точка,
- критическая точка, 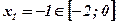 ;
;
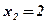 - критическая точка,
- критическая точка, 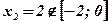 .
.
3) 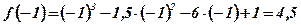 ;
;
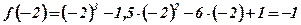 ;
;
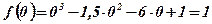 .
.
4) 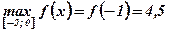 ;
; 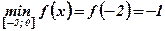 .
.
Ответ: 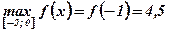 ;
; 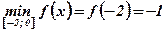 .
.
Упражнения:
- Найти наибольшее и наименьшее значения функции
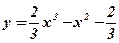 на отрезке
на отрезке 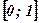 .
.
Изложенный метод поиска наибольшего и наименьшего значений функции применим к решению разнообразных прикладных задач. При этом действуют по следующей схеме:
1. Этап формализации: Задача «переводится» на язык функций. Для этого выбирается удобный параметр х, через который исследуемая величина выражается как функция 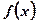 .
.
2. Этап решения математической задачи: Средствами математического анализа находится наибольшее или наименьшее значение функции на некотором промежутке.
3. Этап интерпретации найденного решения: Найденное решение «переводится» с языка математики в терминах первоначальной задачи.
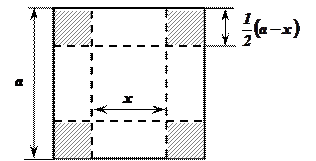
Пример: Из квадратного листа жести со стороной «а» надо изготовить открытую сверху коробку, вырезав по углам квадратики и загнув образовавшиеся кромки. Какой должна быть сторона основания коробки, чтобы ее объем был максимальным?
Решение:
х – длина стороны основания коробки;
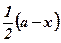 – длина стороны вырезанного квадратика;
– длина стороны вырезанного квадратика;
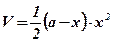 – объем коробки
– объем коробки
По смыслу задачи число х удовлетворяет неравенству 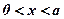 , то есть
, то есть 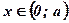 .
.
Таким образом, данная прикладная задача сведена к математической задаче:
найти наибольшее значение функции 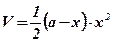 на интервале
на интервале 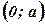 .
.
 | |||
 | |||
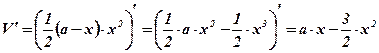 ;
;
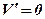 ;
; 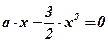 ;
; 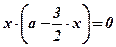 ; х = 0;
; х = 0; 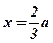 .
.
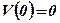 ;
; 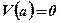 ;
; 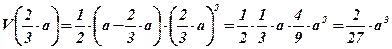 .
.
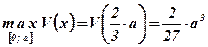 .
.
Функция 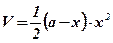 достигает своего наибольшего значения внутри отрезка
достигает своего наибольшего значения внутри отрезка 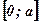 , следовательно, и внутри интервала
, следовательно, и внутри интервала 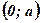 .
.
Так как х – длина стороны основания коробки, имеющей при заданных условиях максимально возможный объем, то максимальный объем, равный 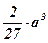 , имеет коробка со стороной основания
, имеет коробка со стороной основания 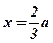 .
.
Ответ: 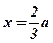 .
.
Пример: Число 36 разделить на такие две части, произведение которых давало бы наибольшее значение.
Решение:
х - первая часть числа 36; 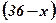 - вторая часть числа 36;
- вторая часть числа 36;
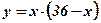 ,
, 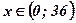 .
.
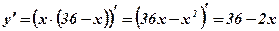 ;
; 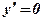 ;
; 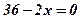 ;
; 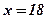 ;
;
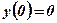 ;
; 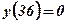 . Функция
. Функция 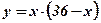 на интервале
на интервале 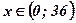 принимает положительные значения, следовательно, наибольшее значение функция принимает при
принимает положительные значения, следовательно, наибольшее значение функция принимает при 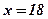 .
.
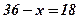 . Число 36 надо разделить на две равные части, произведение которых даст наибольшее значение.
. Число 36 надо разделить на две равные части, произведение которых даст наибольшее значение.
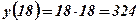 .
.
Ответ: 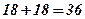 .
.
Упражнения:
Дата: 2018-12-21, просмотров: 380.
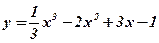 ;
;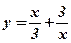 ;
;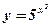 ;
;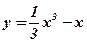 ;
;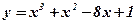 ;
;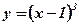 ;
;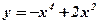 ;
;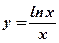 ;
;