
 Рис. 1. Рис. 2. Рис. 3.
Рис. 1. Рис. 2. Рис. 3.
Рис. 4. Рис. 5.
Ответ: Из данных функций непрерывной является функция, изображенная на рис. №3, так как ее график - «неразрывная» (сплошная) линия.
Вопрос: Какими свойствами обладает функция, изображенная на рис. №3, и не обладают другие функции?
Ответ:
1. Функция определена в точке х0. Это свойство не выполняется для функции, изображенной на рис. №1.
2. Существует конечный предел функции в точке х0. Это свойство не выполняется для функций, изображенных на рис. №2, 5.
3. Предел функции в точке х0 равен значению функции в этой точке, то есть 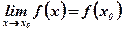 . Это свойство не выполняется для функции, изображенной на рис. №4.
. Это свойство не выполняется для функции, изображенной на рис. №4.
Свойства, которые выполняются для функции, изображенной на рис. №3, и дают возможность дать определение функции непрерывной в точке х0.
Определение: Функция 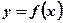 называется непрерывной в точке х0, если
называется непрерывной в точке х0, если 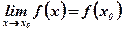 .
.
Замечание: Если функция является непрерывной в точке х0, то точка х0 называется точкой непрерывности функции, если функция не является непрерывной в точке х0, то точка х0 называется точкой разрыва функции.
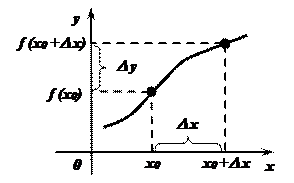 Определение: Функция
Определение: Функция 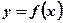 называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
5. Приращение аргумента, приращение функции
Пусть задана функция 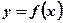 ,
, 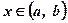 .
.
х0 – начальное значение аргумента, 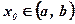 ;
;
х – конечное значение аргумента, 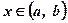 ;
;
f (х0) – начальное значение функции;
f(х0 + D х) – конечное значение функции.
Определение: Разность конечного и начального значений аргумента называется приращением аргумента. D х = х – х0
Определение: Разность конечного и начального значений функции называется приращением функции. D у = f(х0 + D х) – f (х0)
Замечание:
- Геометрически приращение аргумента D х– есть разность абсцисс точек графика функции, соответствующих конечному и начальному значениям аргумента.
- Геометрически приращение функции D у– есть разность ординат точек графика функции, соответствующих конечному и начальному значениям аргумента.
- Приращение аргумента и приращение функции могут быть как положительными, так и отрицательными.
6. Понятие производной функции. Физический смысл производной функции
Рассмотрим задачу о скорости изменения функции 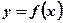 , где х и у могут быть любыми физическими величинами.
, где х и у могут быть любыми физическими величинами.
х0 – начальное значение аргумента; f (х0) – начальное значение функции;
х0 + D х – конечное значение аргумента; f(х0 + D х) – конечное значение функции;
D у = f(х0 + D х) – f (х0) – приращение функции;
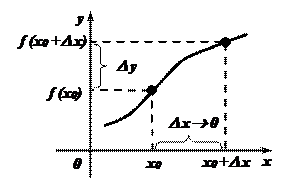
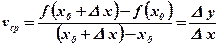
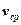 – средняя скорость изменения функции на интервале D х.
– средняя скорость изменения функции на интервале D х.
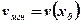 – мгновенная скорость изменения функции, скорость изменения функции в точке х0.
– мгновенная скорость изменения функции, скорость изменения функции в точке х0.
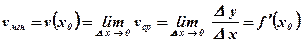
Определение: Производной функции 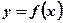 в точке х0 называется предел отношения приращения D у функции в точке х0 к приращению D х аргумента при стремлении приращения аргумента к нулю.
в точке х0 называется предел отношения приращения D у функции в точке х0 к приращению D х аргумента при стремлении приращения аргумента к нулю.
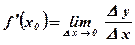
Вывод: Производная функции 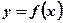 в точке х0 есть скорость изменения функции в точке х0.
в точке х0 есть скорость изменения функции в точке х0.
Теорема: Производная постоянной функции у = с в любой точке 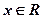 равна нулю.
равна нулю.
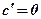
Теорема: Производная функции у = х в любой точке 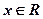 равна единице.
равна единице.
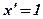 .
.
Замечание: Нахождение производной от данной функции называется дифференцированием.
7. Правила дифференцирования суммы, произведения, частного функций
Рассмотрим функцию 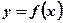 , состоящую из двух других функций
, состоящую из двух других функций 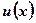 и
и 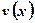 , имеющих производные на отрезке
, имеющих производные на отрезке 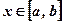 :
:
1) 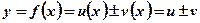 ;
;
2) 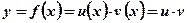 ;
;
3) 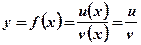 .
.
Теорема №1: Производная суммы (разности) двух функций равна сумме (разности) производных этих функций. 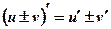
Пример: Вычислить производную функции 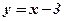
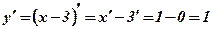 ;
;  .
.
Теорема №2: Производная произведения двух функций определяется по формуле: 
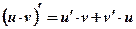
Следствие: Постоянный множитель можно вынести за знак производной: 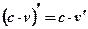 .
.
Доказательство: 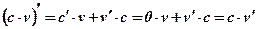 .
.
Пример: Вычислить производные функций:
-
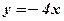 .
. 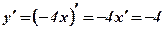 .
. -
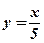 .
. 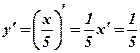 .
. -
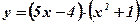 .
.
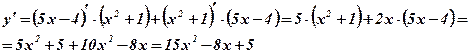
-
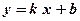 .
. 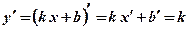 ;
; 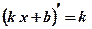 .
.
Упражнения:
1) 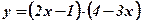 ;
;
2) 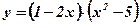 ;
;
3) 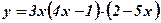 .
.
Производная степенной функции 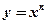 при
при 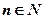 вычисляется по формуле:
вычисляется по формуле:
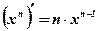
Замечание: Формула 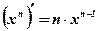 справедлива для степенной функции с любым показателем степени
справедлива для степенной функции с любым показателем степени 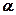 .
. 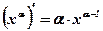 ,
, 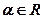
Пример: Вычислить производные функций:
-
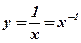 . Решение:
. Решение: 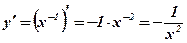 .
. -
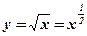 . Решение:
. Решение: 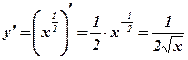 .
. -
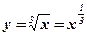 . Решение:
. Решение: 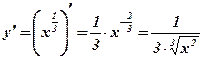 .
. -
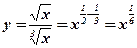 . Решение:
. Решение: 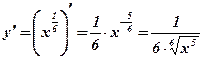 .
.
Вывод: 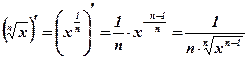 .
.
Упражнения: Вычислить производные функций:
1) 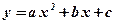 ;
2) ;
2) 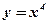 ;
3) ;
3) 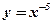 ; ;
| 4) 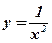 ;
5) ;
5) 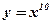 ; ;
| 6) 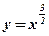 ;
7) ;
7) 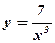 . .
|
Теорема №3: Производная частного двух функций определяется по формуле: 
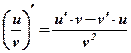
Следствия: 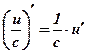 ;
; 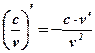
Пример: Вычислить производные функций:
1) 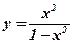 .
.
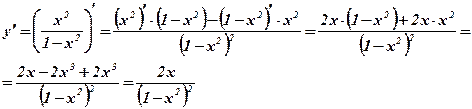
2) 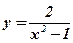 .
. 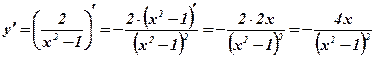 .
.
3) 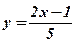 .
. 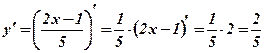 .
.
Упражнения: Вычислить производные функций:
1. 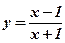 ;
2. ;
2. 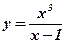 ;
3. ;
3. 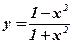 ; ;
|
4. 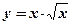 ;
5. ;
5. 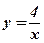 ;
6. ;
6. 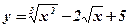 ; ;
|
7. 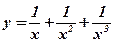 ;
8. ;
8. 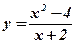 ;
9. ;
9. 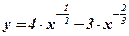 . .
|
8. Понятие сложной функции
Правило дифференцирования сложной функции
Пусть функция 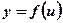 определена на множестве
определена на множестве 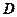 , а функция
, а функция 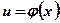 на множестве
на множестве 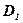 , причем для
, причем для 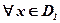 , соответствующее значение
, соответствующее значение 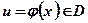 . Тогда на множестве
. Тогда на множестве 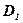 определена функция
определена функция 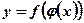 , которая называется сложной функцией от х (функцией от функции).
, которая называется сложной функцией от х (функцией от функции).
Переменную 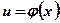 называют промежуточным аргументом сложной функции.
называют промежуточным аргументом сложной функции.
Пример:
-
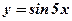 - тригонометрическая, линейная функция;
- тригонометрическая, линейная функция; 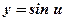 ,
, 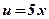 ;
; -
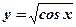 - степенная, тригонометрическая функция;
- степенная, тригонометрическая функция; 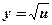 ,
, 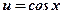 ;
; -
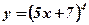 - степенная, линейная функция;
- степенная, линейная функция; 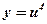 ,
, 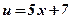 ;
; -
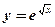 - показательная, степенная функция;
- показательная, степенная функция; 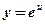 ,
, 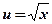 ;
;
Упражнения:
- Из каких элементарных функций состоят данные сложные функции:
1) 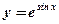 ;
2) ;
2) 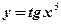 ; ;
| 3) 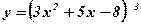 ;
4) ;
4) 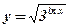 . .
|
- Из данных элементарных функций составить сложные функции:
1) 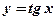 , , 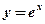 ;
2) ;
2) 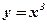 , , 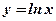 ; ;
| 3) 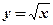 , , 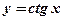 .
4) .
4) 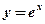 , , 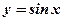 , , 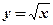 . .
|
Вывод: Производная сложной функции равна произведению производных элементарных функций, ее составляющих.
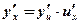
Пример: Вычислить производные функций:
1. 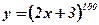 .
.
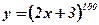 - степенная, линейная;
- степенная, линейная; 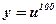 ,
, 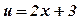 .
.
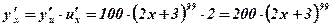 .
.
2. 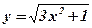 .
.
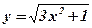 - степенная, квадратичная;
- степенная, квадратичная; 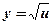 ,
, 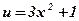 .
.
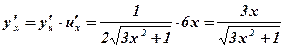 .
.
Упражнения: Вычислить производные функций:
1. 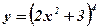 ;
2. ;
2. 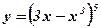 ; ;
|
3. 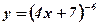 ;
4. ;
4. 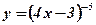 ; ;
| 5. 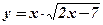 ;
6. ;
6. 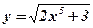 . .
|
9. Производная показательной, логарифмической функций
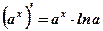
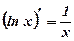
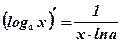
Пример: Вычислить производные функций:
1. 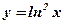 .
. 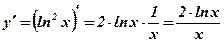 .
.
2. 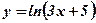 .
. 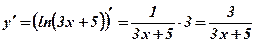 .
.
3. 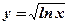 .
. 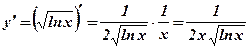 .
.
Пример: Вычислить производные функций:
1. 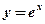 .
. 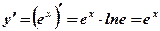 .
.
2. 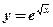 .
. 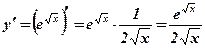 .
.
Упражнения: Вычислить производную функции:
1. 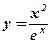 ;
2. ;
2. 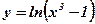 ;
3. ;
3. 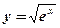 ; ;
| 4. 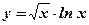 ;
5. ;
5. 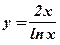 ;
6. ;
6. 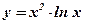 ; ;
| 7. 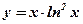 ;
8. ;
8. 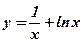 . .
|
10. Производные тригонометрических функций
Производные обратных тригонометрических функций
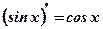 .
.
Пример: Вычислить производные функций:
1. 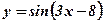 .
. 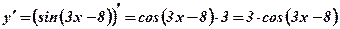 .
.
2. 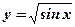 .
. 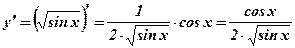 .
.
Задача: Вычислить производную функции 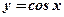 .
.
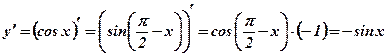 .
. 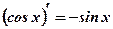 .
.
Задача: Вычислить производную функции 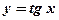 .
.
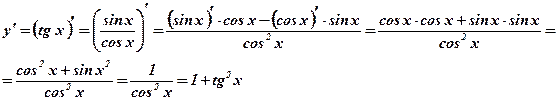
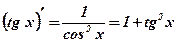 .
.
Упражнение: Вычислить производную функции 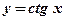 .
.
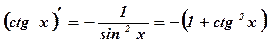 .
.
Дата: 2018-12-21, просмотров: 347.