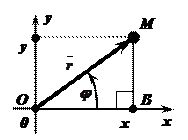 Запись комплексного числа
Запись комплексного числа 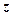 в виде
в виде 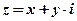 называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.
Рассмотрим 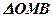 ,
, 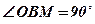 .
.
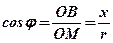 ;
; 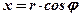
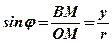 ;
; 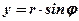
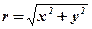 ;
; 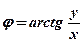
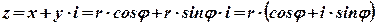
Запись комплексного числа 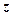 в виде
в виде 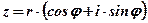 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
Используя формулу Эйлера 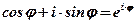 , комплексное число
, комплексное число 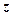 можно записать в так называемой показательной форме:
можно записать в так называемой показательной форме: 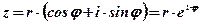 .
.
Запись комплексного числа 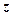 в виде
в виде 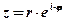 называется показательной формой комплексного числа.
называется показательной формой комплексного числа.
Пример: Представить в тригонометрической и показательной формах комплексные числа:
1. 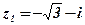 ;
;
Решение: 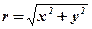 ;
; 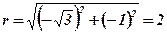 ;
;
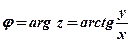 ;
;
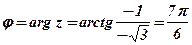 , так как
, так как 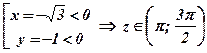 ;
;
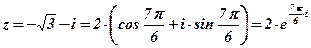 .
.
Ответ: 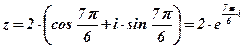 .
.
2. 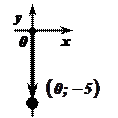
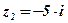 .
.
Решение:
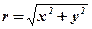 ;
; 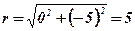 ;
;
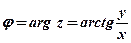 ;
; 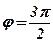 ;
;
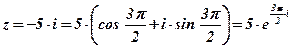 .
.
Ответ: 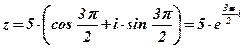 .
.
Вывод:
1) Аргумент действительного числа 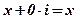 :
: 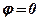 , если
, если 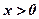 ;
; 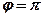 , если
, если 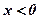 .
.
2) Аргумент мнимого числа 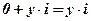 :
: 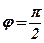 , если
, если  ;
; 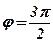 , если
, если 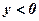 .
.
Упражнения:
- Построить точки, изображающие комплексные числа:
1; – 1; 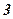 ; i; –5 i;
; i; –5 i; 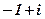 ;
; 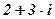 .
.
- Представить в тригонометрической форме комплексные числа:
1; – 1; 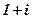 ; i; – i;
; i; – i;  ;
; 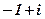 ;
; 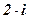 .
.
Действия над комплексными числами
Сложение комплексных чисел, заданных в алгебраической форме
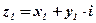 ;
; 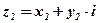 ;
;
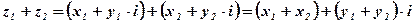
Определение: Суммой двух комплексных чисел 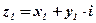 и
и 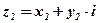 называется комплексное число
называется комплексное число 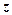 , определяемое равенством
, определяемое равенством
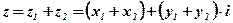 .
.
Частный случай: Сложение сопряжённых комплексных чисел 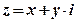 и
и 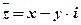 есть число действительное:
есть число действительное:
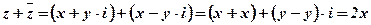
Вычитание комплексных чисел, заданных в алгебраической форме
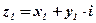 ;
; 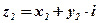 ;
;
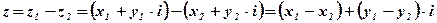
Определение: Разностью двух комплексных чисел 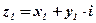 и
и 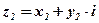 называется такое комплексное число
называется такое комплексное число 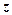 , которое, будучи сложенным с числом
, которое, будучи сложенным с числом 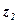 , даёт число
, даёт число 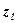 , т. е.
, т. е. 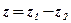 , если
, если 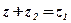 .
.
Частный случай: Вычитание сопряжённых комплексных чисел 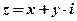 и
и 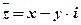 есть число мнимое:
есть число мнимое:
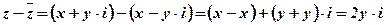
Умножение комплексных чисел, заданных в алгебраической форме
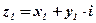 ;
; 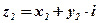 ;
;
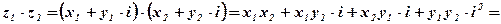
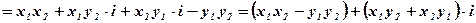
Определение: Произведением двух комплексных чисел 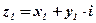 и
и 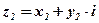 называется комплексное число
называется комплексное число 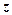 , определяемое равенством
, определяемое равенством
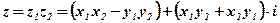
Вывод: 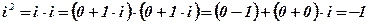 .
.
Пример: 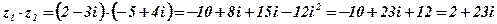 .
.
Частный случай: Произведение сопряжённых комплексных чисел 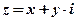 и
и 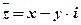 есть число действительное:
есть число действительное:
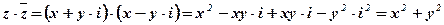
Умножение комплексных чисел, заданных в тригонометрической форме
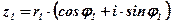 ;
; 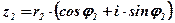
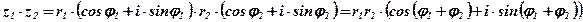
Правило: При умножении комплексных чисел их модули перемножаются, а аргументы складываются.
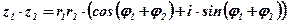
Замечание: Правило умножения комплексных чисел, заданных в тригонометрической форме, распространяется на любое конечное число множителей. В частности, если есть п одинаковых множителей, равных 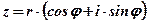 , то
, то
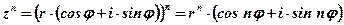 – формула Муавра
– формула Муавра
Правило: При возведении в степень с натуральным показателем комплексного числа его модуль возводится в эту степень, а аргумент умножается на показатель степени.
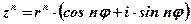
Пример: Найти 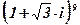 .
.
Решение: Запишем число 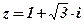 в тригонометрической форме:
в тригонометрической форме:
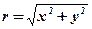 ;
; 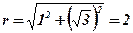 ;
;
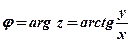 ;
; 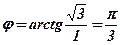 , так как
, так как 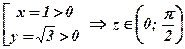 ;
;
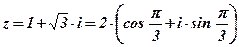 ;
;
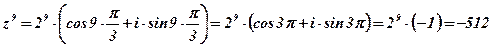 .
.
Ответ: 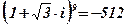 .
.
Рассмотрим степень мнимой единицы 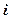 :
:
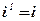 ; ;
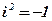 ; ;
|
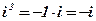 ; ;
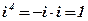
|
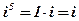 ; ;
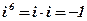 ; ;
|
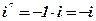 ; ;
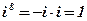
|
Правило: Чтобы возвести мнимую единицу в степень с натуральным показателем, надо возвести её в степень с показателем, равным остатку от деления данного показателя на 4.
Пример: 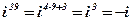 .
.
Дата: 2018-12-21, просмотров: 317.