Расширение понятия числа
Понятие множества является одним из основных неопределяемых понятий математики. Множество, элементами которого являются числа, называется числовым множеством.
Первые представления о числе приобретены людьми в незапамятной древности. Они возникли из счёта людей, животных, предметов.
Определение: Числа, используемые при счёте, называются натуральными.
Обозначение: 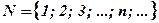 .
.
Расширение понятия числа всегда было связано с необходимостью решения задачи, неразрешимой на известном числовом множестве.
При счёте отдельных предметов единица есть наименьшее число. Но этими числами нельзя обойтись даже в самых простых случаях жизни. Одно натуральное число невозможно в общем случае разделить на другое, если пользоваться только натуральными числами. С введением дробных чисел деление натуральных чисел стало возможным всегда.
Но действие вычитания и после введения дробей остаётся не всегда возможным: нельзя вычесть большее число из меньшего числа. В силу того, что в повседневной жизни нет необходимости выполнять подобное вычитание, оно долгое время считалось не только невозможным, но и совершенно бессмысленным. Развитие алгебры показало, что такое действие необходимо ввести в математику. Исторически отрицательные числа возникли в связи с решением уравнений. До введения отрицательных чисел можно было говорить, что уравнение 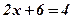 не имеет корней. Однако после введения отрицательных чисел это уравнение стало разрешимым.
не имеет корней. Однако после введения отрицательных чисел это уравнение стало разрешимым.
Если же мы хотим сделать вычитание всегда возможным, мы должны «отсутствие числа» также считать числом. В математику был введён нуль (буквальный смысл латинского слова nullum – «ничто»).
Определение: Натуральные числа, числа противоположные натуральным и нуль образуют множество целых чисел.
Обозначение: 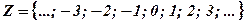
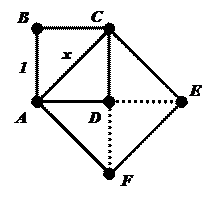 Целых и дробных чисел достаточно для измерительной практики. Однако, для теории измерения этих чисел мало.
Целых и дробных чисел достаточно для измерительной практики. Однако, для теории измерения этих чисел мало.
Пусть требуется точно измерить длину диагонали АС квадрата АВС D, сторона которого равна 1 м. Площадь квадрата А CEF, построенного на диагонали, равна удвоенной площади АВС D.
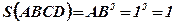
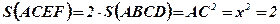
Никакое целое и дробное число не могут удовлетворить уравнению  .
.
Оставалось одно из двух: или отказаться от точного выражения длин числами, или ввести новые числа.
Числа, которые нельзя выразить целым или дробным числом, назвали иррациональными числами. Числа 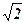 ,
, 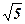 и многие другие выражения, содержащие рациональные числа под знаком радикала, иррациональны. Однако ими не исчерпывается запас иррациональных чисел. Множество иррациональных чисел содержит трансцендентные числа:
и многие другие выражения, содержащие рациональные числа под знаком радикала, иррациональны. Однако ими не исчерпывается запас иррациональных чисел. Множество иррациональных чисел содержит трансцендентные числа: 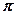 ,
, 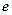 ,
, 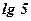 и т. д.
и т. д.
Замечание: В противоположность иррациональным числа целые и дробные получили название рациональных.
Определение: Множество рациональных чисел, это множество чисел, представимых в виде обыкновенной дроби 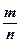 , где т и п - целые числа.
, где т и п - целые числа.
Обозначение: 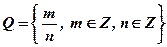 .
.
Определение: Объединение множества рациональных чисел с множеством иррациональных чисел называется множеством действительных чисел.
Обозначение: 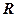 – множество действительных чисел.
– множество действительных чисел.
Введение комплексных чисел также связано с решением уравнений.
Уравнение 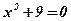 , не имеющее решений на множестве действительных чисел, становится разрешимым после введения новых величин – квадратных корней из отрицательных чисел. Эти величины были впервые введены итальянским математиком Кардано в середине XVI века в связи с решением кубического уравнения. Декарт в 30-х годах XVII века ввёл наименование «мнимые числа».
, не имеющее решений на множестве действительных чисел, становится разрешимым после введения новых величин – квадратных корней из отрицательных чисел. Эти величины были впервые введены итальянским математиком Кардано в середине XVI века в связи с решением кубического уравнения. Декарт в 30-х годах XVII века ввёл наименование «мнимые числа».
Замечание: Именно в противоположность мнимым числам прежде известные числа (положительные и отрицательные, в том числе иррациональные) стали называться действительными или вещественными.
Итальянские математики XVI века Кардано и Бомбелли, решая квадратные уравнения вида 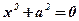 , ввели в рассмотрение символ
, ввели в рассмотрение символ 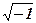 , который в XVIII веке петербургский математик Л. Эйлер (1708-1783) обозначил i.
, который в XVIII веке петербургский математик Л. Эйлер (1708-1783) обозначил i.
Пример: Решить уравнение:
1) 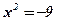 .
.
Решение: 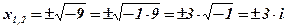 . Ответ:
. Ответ: 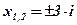
2) 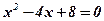 .
.
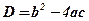 ;
; 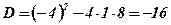 ;
;
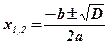 ;
; 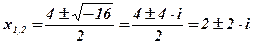 . Ответ:
. Ответ: 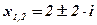 .
.
Основные понятия теории комплексных чисел
Определение: Комплексным числом называется выражение вида 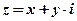 , где х и у – действительные числа, а i – мнимая единица, обладающая свойством
, где х и у – действительные числа, а i – мнимая единица, обладающая свойством 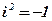 .
.
Вывод:
-
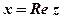 – действительная часть комплексного числа
– действительная часть комплексного числа 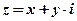 .
. -
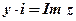 – мнимая часть комплексного числа
– мнимая часть комплексного числа 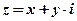 .
. -
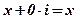 – действительное число.
– действительное число. -
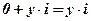 – мнимое число.
– мнимое число. - Множество
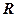 действительных чисел является подмножеством множества
действительных чисел является подмножеством множества 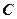 комплексных чисел.
комплексных чисел.
Определение: Два комплексных числа называются равными тогда и только тогда, когда равны их действительные части и равны их мнимые части.
Обозначение: 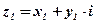 ;
; 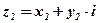 .
. 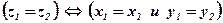
Определение: Комплексное число 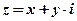 равно нулю тогда и только тогда, когда
равно нулю тогда и только тогда, когда 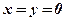 .
.
Обозначение: 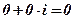 .
.
Определение: Два комплексных числа, отличающиеся лишь знаком мнимой части, называются сопряженными.
Обозначение: 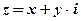 и
и 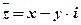 – сопряжённые комплексные числа.
– сопряжённые комплексные числа.
Расширение понятия числа
Понятие множества является одним из основных неопределяемых понятий математики. Множество, элементами которого являются числа, называется числовым множеством.
Первые представления о числе приобретены людьми в незапамятной древности. Они возникли из счёта людей, животных, предметов.
Определение: Числа, используемые при счёте, называются натуральными.
Обозначение: 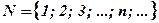 .
.
Расширение понятия числа всегда было связано с необходимостью решения задачи, неразрешимой на известном числовом множестве.
При счёте отдельных предметов единица есть наименьшее число. Но этими числами нельзя обойтись даже в самых простых случаях жизни. Одно натуральное число невозможно в общем случае разделить на другое, если пользоваться только натуральными числами. С введением дробных чисел деление натуральных чисел стало возможным всегда.
Но действие вычитания и после введения дробей остаётся не всегда возможным: нельзя вычесть большее число из меньшего числа. В силу того, что в повседневной жизни нет необходимости выполнять подобное вычитание, оно долгое время считалось не только невозможным, но и совершенно бессмысленным. Развитие алгебры показало, что такое действие необходимо ввести в математику. Исторически отрицательные числа возникли в связи с решением уравнений. До введения отрицательных чисел можно было говорить, что уравнение 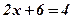 не имеет корней. Однако после введения отрицательных чисел это уравнение стало разрешимым.
не имеет корней. Однако после введения отрицательных чисел это уравнение стало разрешимым.
Если же мы хотим сделать вычитание всегда возможным, мы должны «отсутствие числа» также считать числом. В математику был введён нуль (буквальный смысл латинского слова nullum – «ничто»).
Определение: Натуральные числа, числа противоположные натуральным и нуль образуют множество целых чисел.
Обозначение: 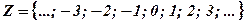
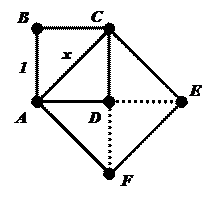 Целых и дробных чисел достаточно для измерительной практики. Однако, для теории измерения этих чисел мало.
Целых и дробных чисел достаточно для измерительной практики. Однако, для теории измерения этих чисел мало.
Пусть требуется точно измерить длину диагонали АС квадрата АВС D, сторона которого равна 1 м. Площадь квадрата А CEF, построенного на диагонали, равна удвоенной площади АВС D.
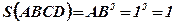
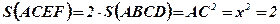
Никакое целое и дробное число не могут удовлетворить уравнению  .
.
Оставалось одно из двух: или отказаться от точного выражения длин числами, или ввести новые числа.
Числа, которые нельзя выразить целым или дробным числом, назвали иррациональными числами. Числа 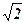 ,
, 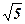 и многие другие выражения, содержащие рациональные числа под знаком радикала, иррациональны. Однако ими не исчерпывается запас иррациональных чисел. Множество иррациональных чисел содержит трансцендентные числа:
и многие другие выражения, содержащие рациональные числа под знаком радикала, иррациональны. Однако ими не исчерпывается запас иррациональных чисел. Множество иррациональных чисел содержит трансцендентные числа: 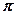 ,
, 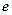 ,
, 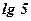 и т. д.
и т. д.
Замечание: В противоположность иррациональным числа целые и дробные получили название рациональных.
Определение: Множество рациональных чисел, это множество чисел, представимых в виде обыкновенной дроби 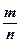 , где т и п - целые числа.
, где т и п - целые числа.
Обозначение: 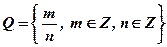 .
.
Определение: Объединение множества рациональных чисел с множеством иррациональных чисел называется множеством действительных чисел.
Обозначение: 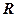 – множество действительных чисел.
– множество действительных чисел.
Введение комплексных чисел также связано с решением уравнений.
Уравнение 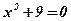 , не имеющее решений на множестве действительных чисел, становится разрешимым после введения новых величин – квадратных корней из отрицательных чисел. Эти величины были впервые введены итальянским математиком Кардано в середине XVI века в связи с решением кубического уравнения. Декарт в 30-х годах XVII века ввёл наименование «мнимые числа».
, не имеющее решений на множестве действительных чисел, становится разрешимым после введения новых величин – квадратных корней из отрицательных чисел. Эти величины были впервые введены итальянским математиком Кардано в середине XVI века в связи с решением кубического уравнения. Декарт в 30-х годах XVII века ввёл наименование «мнимые числа».
Замечание: Именно в противоположность мнимым числам прежде известные числа (положительные и отрицательные, в том числе иррациональные) стали называться действительными или вещественными.
Итальянские математики XVI века Кардано и Бомбелли, решая квадратные уравнения вида 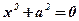 , ввели в рассмотрение символ
, ввели в рассмотрение символ 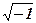 , который в XVIII веке петербургский математик Л. Эйлер (1708-1783) обозначил i.
, который в XVIII веке петербургский математик Л. Эйлер (1708-1783) обозначил i.
Пример: Решить уравнение:
1) 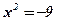 .
.
Решение: 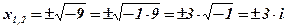 . Ответ:
. Ответ: 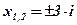
2) 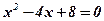 .
.
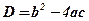 ;
; 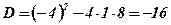 ;
;
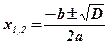 ;
; 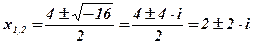 . Ответ:
. Ответ: 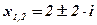 .
.
Основные понятия теории комплексных чисел
Определение: Комплексным числом называется выражение вида 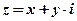 , где х и у – действительные числа, а i – мнимая единица, обладающая свойством
, где х и у – действительные числа, а i – мнимая единица, обладающая свойством 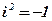 .
.
Вывод:
-
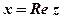 – действительная часть комплексного числа
– действительная часть комплексного числа 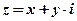 .
. -
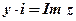 – мнимая часть комплексного числа
– мнимая часть комплексного числа 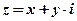 .
. -
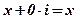 – действительное число.
– действительное число. -
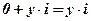 – мнимое число.
– мнимое число. - Множество
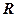 действительных чисел является подмножеством множества
действительных чисел является подмножеством множества 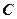 комплексных чисел.
комплексных чисел.
Определение: Два комплексных числа называются равными тогда и только тогда, когда равны их действительные части и равны их мнимые части.
Обозначение: 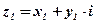 ;
; 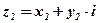 .
. 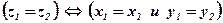
Определение: Комплексное число 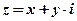 равно нулю тогда и только тогда, когда
равно нулю тогда и только тогда, когда 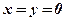 .
.
Обозначение: 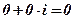 .
.
Определение: Два комплексных числа, отличающиеся лишь знаком мнимой части, называются сопряженными.
Обозначение: 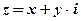 и
и 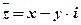 – сопряжённые комплексные числа.
– сопряжённые комплексные числа.
Геометрическое изображение комплексного числа
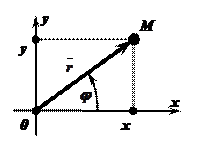 Всякое комплексное число
Всякое комплексное число 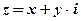 можно изобразить точкой
можно изобразить точкой 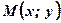 плоскости Оху. И, наоборот, каждую точку
плоскости Оху. И, наоборот, каждую точку 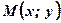 координатной плоскости можно рассматривать как образ комплексного числа
координатной плоскости можно рассматривать как образ комплексного числа 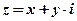 .
.
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью.
Ось абсцисс называется действительной осью, так как на ней лежат действительные числа 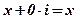 .
.
Ось ординат называется мнимой осью, так как на ней лежат мнимые числа 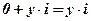 .
.
Комплексное число 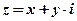 можно задавать с помощью радиус-вектора
можно задавать с помощью радиус-вектора 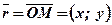 точки
точки 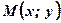 .
.
Определение: Модулем комплексного числа 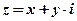 называется длина радиус-вектора
называется длина радиус-вектора 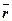 , изображающего это комплексное число.
, изображающего это комплексное число.
Обозначение: 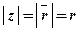 – модуль комплексного числа
– модуль комплексного числа 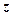 .
.
Определение: Аргументом комплексного числа 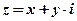 называется наименьший угол между положительным направлением действительной оси и радиус-вектором
называется наименьший угол между положительным направлением действительной оси и радиус-вектором 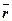 , изображающим это комплексное число.
, изображающим это комплексное число.
Обозначение: 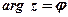 – аргумент комплексного числа
– аргумент комплексного числа 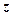 .
.
Вывод:
- Аргумент комплексного числа
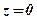 не определён.
не определён. - Аргумент комплексного числа
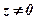
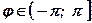 , т. е.
, т. е. 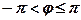 .
.
Упражнения:
- Изобразить на комплексной плоскости числа:
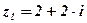 ;
; 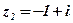 ;
;  ;
; 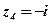 ;
; 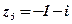 ;
; 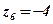 .
. - Найти числа сопряжённые для данных комплексных чисел:
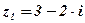 ;
; 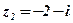 ;
; 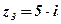 ;
; 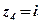 ;
; 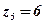 . Построить их на комплексной плоскости.
. Построить их на комплексной плоскости. - Решить уравнения:
1) 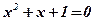 ;
2) ;
2) 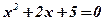 ; ;
| 3) 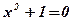 ;
4) ;
4) 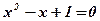
| 5) 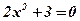 ;
6) ;
6) 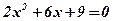 . .
|
Дата: 2018-12-21, просмотров: 310.