Динамика интегрирующего звена описывается дифференциальным уравнением
.
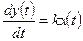1. Переходная характеристика:
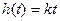
2. Импульсная переходная характеристика (или функция веса) имеет вид:
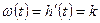
3. Передаточная функция идеального интегрирующего звена:
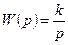
4. АФХ звена:
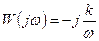
на комплексной плоскости изображается в виде прямой, совпадающей с мнимой осью.
5. АЧХ:
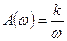
представляет собой гиперболу, которая при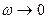 
стремится к бесконечности. При увеличении частоты значения А( w ) стремятся к нулю. Это свойство сближает интегрирующие звенья с инерционными.
6. ФЧХ идеального интегрирующего звена:
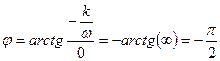
показывает, что сдвиг фаз, создаваемый звеном, на всех частотах одинаков и равен
-900.
7. ЛАЧХ:
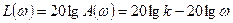
представляет собой прямую с наклоном –20дБ/декаду, проходящую через точку с координатами w=1, L ( w )=20lgk.
 |
Пример:
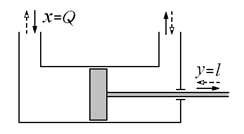Идеальным интегрирующим звеном можно считать (с некоторыми допущениями) гидравлический исполнительный механизм, для которого входной и выходной величиной является количество жидкости Q (м3/с), поступающей в единицу времени в полость цилиндра, а выходной величиной – перемещение l (м) поршня со штоком. Действительно, если масса перемещающихся частей пренебрежимо мала и усилие, создаваемое давлением гидронасоса, существенно больше сил сопротивления, то перемещение поршня определяется уравнением баланса жидкости вида
,
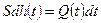где S – площадь поверхности жидкости (м2), а коэффициент k – выражением
.
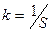Идеальных интегрирующих звеньев в реальных объектах практически не существует.
Реальное интегрирующее звено
Динамика процесса в таком звене описывается следующим уравнением:
,
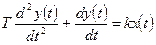где k – коэффициент усиления.
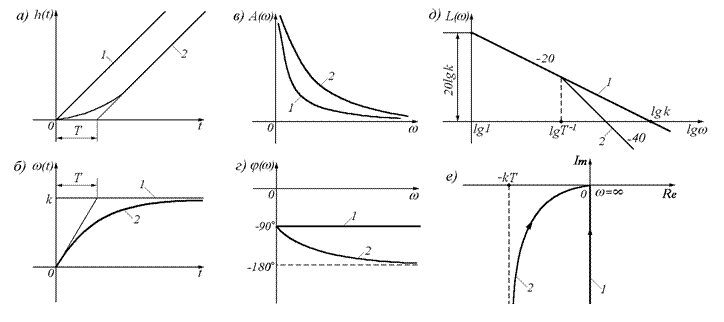
1. Переходная характеристика:
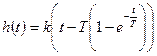
2. Импульсная переходная характеристика:
3. Передаточная функция реального интегрирующего звена:
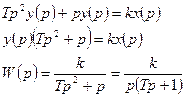
Реальное интегрирующее звено представляет собой последовательное соединение идеального интегрирующего звена и апериодического.
4. АФХ:
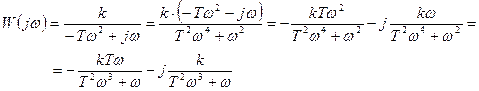
5. АЧХ:
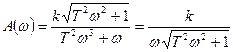
6. ФЧХ:
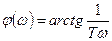
7. ЛАЧХ:
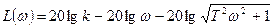
Структурная схема:
Примером может служить электродвигатель постоянного тока, в котором управляемая величина – поворот вала двигателя.
Изодромное интегрирующее звено
Динамика процесса описывается следующим уравнением:
,
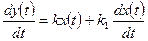здесь k и k 1 – коэффициенты усиления.
1. Переходная характеристика:
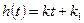
2. Импульсная переходная характеристика:
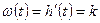
3. Передаточная функция:
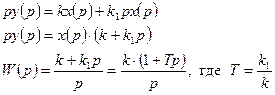
4. АФХ:
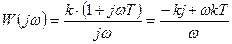
5. АЧХ:
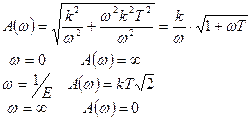
6. ФЧХ:
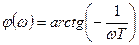
7. ЛАЧХ:
 |
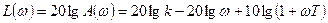
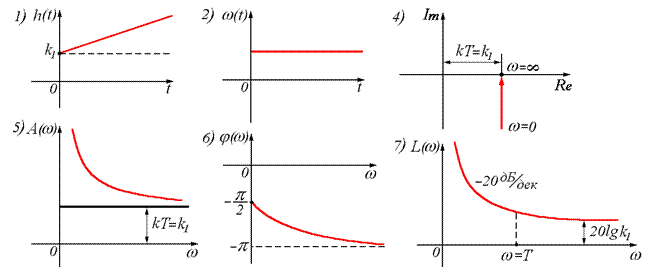Структурная схема:
Примером изодромного интегрирующего звена может служить гидравлический демпфер, к поршню которого присоединена пружина.
Дата: 2018-12-21, просмотров: 633.
