ПРАВИЛА ПО МАТЕМАТИКЕ
ЧИСЛА И ЦИФРЫ.
Числа – это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т.д.).
Для записи чисел используются специальные знаки – цифры.
Цифр – десять:
1 2 3 4 5 6 7 8 9 0
НАТУРАЛЬНЫЕ ЧИСЛА.
Числа, которые используются при счёте, называются натуральными.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …, □
1 – самое маленькое число.
□ – самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль не является натуральным число.
СРАВНЕНИЕ ЧИСЕЛ.
Правило 1.
Из двух натуральных чисел больше то, которое в натуральном ряду расположено правее, а меньше то, которое расположено левее:
…, 10, 11, 12, 13, 14, 15,
14 > 11
Правило 2.
Из двух натуральных чисел с разным количеством разрядов больше то число, в котором разрядов больше.
28 < 145 782 < 1263
Правило 3.Из двух натуральных чисел с одинаковым количеством разрядов больше то, у которого больше цифра старшего разряда.
45 861 < 47 361 47361 > 45 681
СЛОЖЕНИЕ.
Сложение – это математическое действие.
Числа, которые складываются, называются слагаемыми.
Результат сложения называется суммой.
a + b = c
первое слагаемое второе слагаемое сумма
Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое .
Если одно из слагаемых равно 0, сумма равна второму слагаемому:
a + 0 = 0 + a = a
ВЫЧИТАНИЕ.
Вычитание – действие, обратное сложению.
a - b = c
уменьшаемое вычитаемое разность
Правило 1.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Правило 2.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Правило 1.
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое, а из полученного результата (разности) вычесть второе слагаемое.
Например:
126 — (56 + 30) = (126 — 56) — 30 = 40.
а — (Ь + с) = (а — Ь) — с.
Правило 2.
Чтобы вычесть число из суммы, можно вычесть его из одного из слагаемых и к результату прибавить второе слагаемое.
Например:
(71 + 7) — 51 = (71 — 51) + 7 = 20 + 7 = 27, но нельзя (71 + 7) — 51 = (7 — 51) + 71,так как разность (7 — 51) — ненатуральное число.
В общем виде: (а + Ь) — с = (а — с) + Ь.
ЗАКОНЫ СЛОЖЕНИЯ.
Закон 1.
Переместительный закон сложения.
a + b = b + a
От перемены мест слагаемых значение суммы не меняется:
4 + 2 = 2 + 4
Закон 2.
Сочетательный закон сложения.
(a + b) + c = a + (b + c) = (a + c) + b
(2 + 4) + 8 = 2 + (4 + 8) = (2 + 8) + 4
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел или ко второму числу прибавить сумму первого и третьего чисел:
УМНОЖЕНИЕ.
Умножение – это сложение одинаковых слагаемых.
2 + 2 + 2 = 2 х 3 = 6
(по два три раза )
a · х b = c
Первый множитель второй множитель произведение
2 ·х 3 = 6
Чтобы найти неизвестный множитель надо произведение разделить на известный множитель.
6: 2=3 6:3=2
ЗАКОНЫ УМНОЖЕНИЯ.
Закон 1.
Переместительный закон умножения.
От перестановки множителей произведение не меняется:
a х· b = b х· a
4 ·х 2 = 2 ·х 4
8 = 8
Закон 2.
Сочетательный закон умножения.
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел или второе число умножить на произведении первого и третьего чисел:
( a х· b ) х· c = a ·х ( b ·х c ) = ( a ·х c ) ·х b
(2 ·х 4) х· 8 = 2 х· (4 х· 8) = (2 ·х 8) ·х 4
64=64
Закон 3.
Распределительный закон умножения.
Относительно сложения
Произведение суммы на число равно сумме произведений каждого слагаемого на это число.
(a + b + c) ·х d = a х· d + b х· d + c х· d
(2 + 5 + 3) · 2 = 2 ·х 2 + 5 ·х 2 + 3 х· 2 = 20
Относительно вычитания
Чтобы умножить разность на число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение.
(a - b) х· d = a х· d - b ·х d
(15 - 5) х· 4 = 15 х· 4 - 5 х· 4 = 60 - 20 = 40
ОСОБЫЕ СЛУЧАИ УМНОЖЕНИЯ.
a ·х 1 = a
4 х· 1 = 4
1 х· a = a
1 х· 4 = 4
0 ·х a = 0
0 х· 6 = 0
a х· 0 = 0
ДЕЛЕНИЕ.
Деление – это действие, обратное умножению.
a : b = c
Делимое делитель частное
6 : 3 = 2
Чтобы найти делимое, надо частное умножить на делитель.
2 х 3=6
Чтобы найти делитель надо делимое разделить на частное.
6 : 2=3
СВОЙСТВА ДЕЛЕНИЯ.
Правило 1.
Чтобы разделить сумму на число, достаточно разделить каждое слагаемое на это число, а полученные результаты сложить.
(a + b) : c = a : c + b : c
(8+6) :2 = 8 : 2 + 6 : 2
Правило 2.
Единицы измерения длины
1 см = 10 мм1 дм = 10 см
1 м = 10 дм = 100 см = 1000 мм
1 км = 1000 м = 10000 дм = 100000 см
Единицы измерения массы
1 кг = 1000 г
1 ц = 100 кг
1 т = 10 ц = 1000 кг
Единицы измерения времени
1 мин = 60 с
1 ч = 60 мин = 3600 с
1 сутки = 24 часа
1 неделя = 7 дней
1 месяц = 30 или 31 день (в феврале 28 или 29 дней)
1 год = 12 месяцев = 52 недели = 365 или 366 дней
1 век (столетие) = 100 лет
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Периметр треугольника
P. = a + b + c
Периметр прямоугольника
P = (a + b) · 2
Р= (3+6) х2
Р= 18 см
Периметр квадрата
P = a · 4
Р= 5х4
Р= 20 см
Дробь
Дробь – это число, которое состоит из одной или более частей единицы. Дробное число записывается в виде двух чисел, разделенных горизонтальной чертой. При этом верхнее (или первое) называется числителем, а нижнее (второе) - знаменателем. –
Сложение и вычитание дробей.
При сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) .:
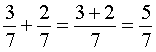
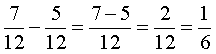
Нахождение части числа.
Чтобы найти часть числа, выраженную дробью, можно это число разделить на знаменатель дроби и полученный результат умножить на ее числитель.
Чтобы найти ¾ числа 24, можно это число разделить на знаменатель дроби 4 и полученный результат умножить на числитель 3.
24: 4 х 3=18
ПРАВИЛА ПО МАТЕМАТИКЕ
ЧИСЛА И ЦИФРЫ.
Числа – это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т.д.).
Для записи чисел используются специальные знаки – цифры.
Цифр – десять:
1 2 3 4 5 6 7 8 9 0
НАТУРАЛЬНЫЕ ЧИСЛА.
Числа, которые используются при счёте, называются натуральными.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …, □
1 – самое маленькое число.
□ – самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль не является натуральным число.
СРАВНЕНИЕ ЧИСЕЛ.
Правило 1.
Из двух натуральных чисел больше то, которое в натуральном ряду расположено правее, а меньше то, которое расположено левее:
…, 10, 11, 12, 13, 14, 15,
14 > 11
Правило 2.
Дата: 2018-12-21, просмотров: 491.