Назначаем предельные отклонения на все размеры составляющих звеньев размерной цепи (кроме специального звена) как на основные валы или отверстия соответственно по h7 и H7:
А1=18+0,1 (задан);
А2=140-0,040;
А3= 18+0,1 (задан);
А4=24+0,021;
А6= А6 сп=?.
Определяем координаты середин полей допусков замыкающего и составляющих звеньев размерной цепи:
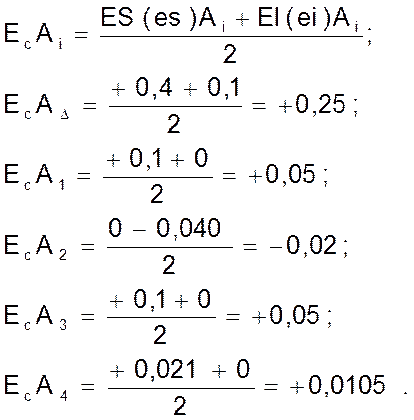
Определяем координату середины поля допуска специального звена:
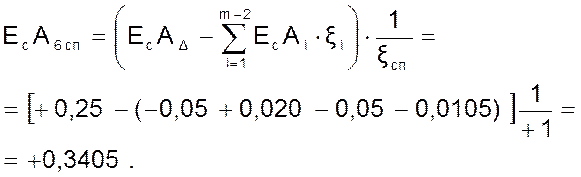
Определяем предельные отклонения специального звена:
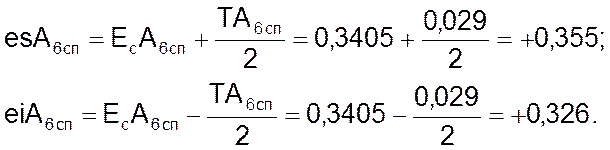
Таким образом, расчетное значение специального звена: 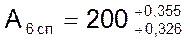 .
.
Подбираем ближайшее стандартное значение основного отклонения специального звена. Расчетное основное отклонение специального звена – нижнее eiА6 сп=+326 мкм. По таблице числовых значений основных отклонений ГОСТ 25346-89 (прил.1, табл. 6) выбираем два стандартных основных отклонения (так как расчетное значение расположено примерно посередине): v (eiА6 сп=+284 мкм) – меньше расчетного и x (eiА6 сп=+350 мкм) – больше расчетного.
Второе предельное отклонение рассчитываем по формуле
esА6 сп=eiА6 сп+ТА6 сп.
Таким же образом далее рассматриваем два варианта стандартных значений специального звена:
Вариант І
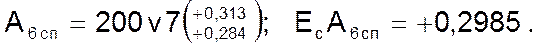
Вариант ІІ 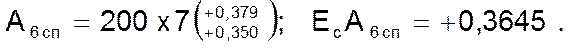
4.2.4. Проверяем правильность решения прямой задачи (обратная задача)
Вариант І

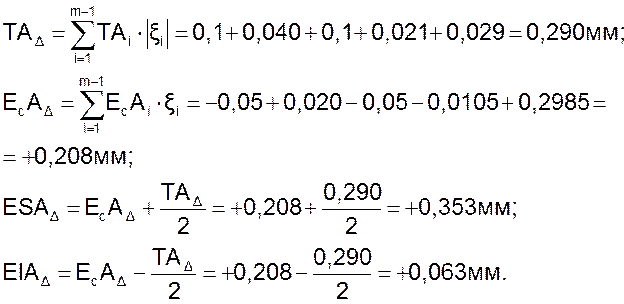
Расчетное значение замыкающего звена по первому варианту: 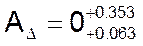 .
.
Вариант ІІ
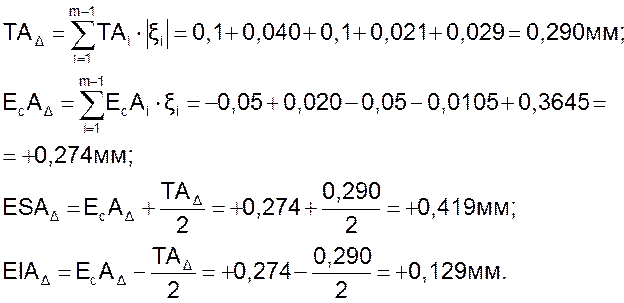
Расчетное значение замыкающего звена по ІІ варианту:
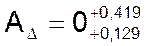 .
.
Сравнивая варианты І и ІІ, можно увидеть, что ни один из вариантов не отвечает требуемым соотношениям (3.19) между рассчитанными и заданными параметрами исходного звена. Для дальнейшей корректировки расчетов выбираем вариант ІI, так как значение 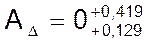 расположено ближе к заданному.
расположено ближе к заданному.
4.2.5. Вводим второе специальное звено, в качестве которого выбираем звено А4 = А4сп. Назначаем для него (вместо H7) поле допуска F7 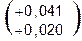 . Координата середины поля допуска звена
. Координата середины поля допуска звена 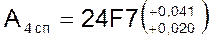 также изменится:
также изменится:
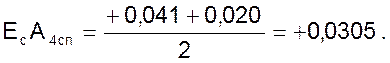
Подставляем новое значение ЕсА4сп в формулу расчета середины поля допуска замыкающего звена:
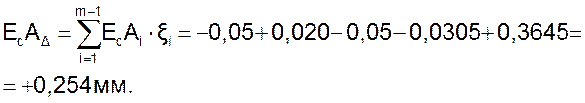
Откуда:
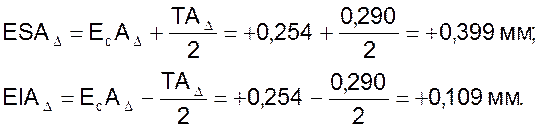
Таким образом, полученное значение 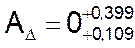 отвечает требованиям, предъявляемым к исходному звену.
отвечает требованиям, предъявляемым к исходному звену.
4.2.6. Вывод: требуемая точность исходного звена при расчетах методом полной взаимозаменяемости достигается при следующих размерах составляющих звеньев:
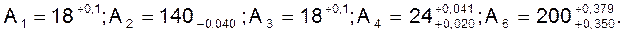
Вместе с тем метод полной взаимозаменяемости в данном случае неприемлем, так как не обеспечивается требование средней экономической точности (составляющие звенья приходится изготавливать по 6 и 7 квалитетам).
Решение прямой задачи методом неполной взаимозаменяемости (расчеты ведутся вероятностным методом)
4.3.1. Решение уравнения номинальных размеров (см 4.2.1):
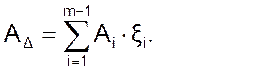
Дата: 2018-12-21, просмотров: 463.