3.2.1. Определение допусков составляющих звеньев размерной цепи

Допуски составляющих звеньев определяются из основного уравнения точности размерной цепи:

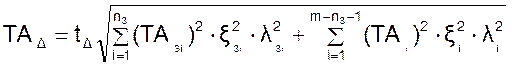(3.20)

1. Если номинальные размеры составляющих звеньев размерной цепи равны или близки по их значениям, то, используя способ равных допусков, из (3.20) определяют среднюю величину допуска составляющих звеньев (T_срA_i):                   

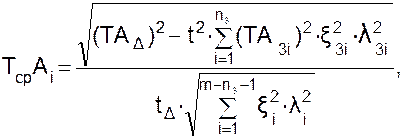     (3.21)

где t_D - коэффициент риска для замыкающего звена;

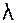_i - относительное среднее квадратическое отклонение i-го составляющего звена размерной цепи;

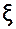_зi и _зi 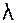- передаточное отношение и относительное среднее квадратическое отклонение составляющего звена размерной цепи с заранее заданными допусками.

Коэффициент риска t_D выбирается в зависимости от риска Р (прил. 1, табл. 2).

Значение относительного среднего квадратического отклонения принимается равным:

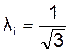, если при расчете неизвестен характер кривой распределения размеров звеньев, что характерно для изделий индивидуального и мелкосерийного производства, или необходимо обеспечить высокую точность изготовления звеньев - выше 5-го квалитета;

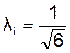, если предполагается, что кривая рассеяния соответствует закону Симпсона (треугольника), что встречается, как правило, при изготовлении звеньев по 6, 7, 8-м квалитетам;

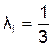, если предполагается, что кривая рассеяния соответствует нормальному закону распределения встречающемуся при точности изготовления звеньев по квалитетам не ниже 8-го (чаще всего для изделий крупносерийного и массового производства).

2. В случае значительного различия в номинальных размерах составляющих звеньев размерной цепи для определения их допусков сначала устанавливают квалитет, одинаковый для всех составляющих звеньев (способ равных квалитетов).

Для этого рассчитывают коэффициент К_ср, определяющий число единиц допуска i в допуске составляющих звеньев TA_i:

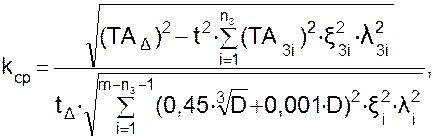    (3.22)

Аналогично п. 3. подбирают квалитеты составляющих звеньев размерной цепи. Далее устанавливают допуски на все звенья размерной цепи, кроме одного – специального, а также назначают предельные отклонения (п.3.1.2.).

Затем определяют допуск и предельные отклонения специального звена.

Допуск на специальное звено рассчитывается по формуле:

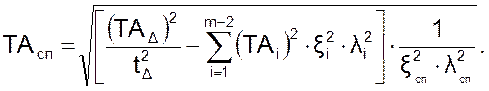(3.23)

Полученная расчетом по (3.23) величина допуска TA_сп должна быть уточнена подбором ближайшего (меньшего) стандартного значения. Таким образом, получаем квалитет, по которому должно изготавливаться специальное звено.

Предельные отклонения специального звена определяют по формулам (3.15).

Координату середины поля допуска специального звена определяют по формуле:

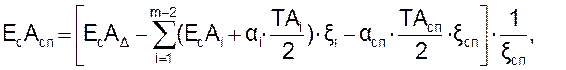(3.24)

где 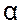_i – коэффициент асимметрии кривой распределения составляющих звеньев размерной цепи:

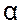       _сп – коэффициент асимметрии кривой распределения специального звена размерной цепи.

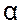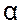Для симметричных законов распределения (равномерного, Симпсона, нормального) установлено: _i= _сп=0.

Тогда координата середины поля допуска специального звена определяется по формуле (3.16).

Далее аналогично п.3.1.2. определяют основное и второе предельное отклонения специального звена.

3.2.3. Проверка правильности решения прямой задачи

Проверка правильности решения прямой задачи методом неполной взаимозаменяемости осуществляется путем решения обратной задачи – по рассчитанным параметрам составляющих звеньев размерной цепи определяют параметры замыкающего звена, решая уравнения:

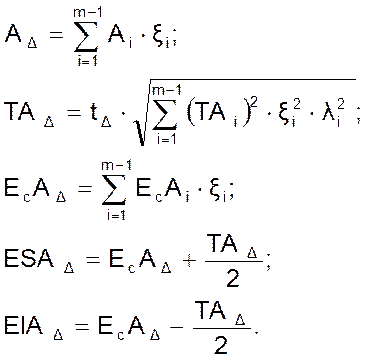                 (3.25)

Прямая задача решена правильно, если выполняются соотношения (3.19) между рассчитанными и заданными параметрами исходного звена.

Если соотношения (3.19) не выполнены, то необходимо добиться их выполнения так же, как и в п.3.1.3.

Вывод о применении метода неполной взаимозаменяемости делается так же, как и в п.3.1.3.