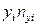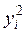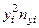Понятие корреляции и корреляционный анализ. Корреляция метрических переменных. Расчет коэффициентов корреляции. Проверка гипотез об отличии корреляции. Сравнение корреляций для зависимых и независимых выборок. Корреляция ранговых переменных. Анализ корреляционных матриц.
Тема 3. Регрессионный анализ.
Эмпирические математические модели. Математико-статистические идеи метода. Классификация многомерных методов по исходным предположениям о структуре данных. Линейная регрессия. Многофакторная линейная регрессия. Оценка уровней значимости коэффициентов регрессионного уравнения. Нелинейная регрессия.
Тема 4. Основы факторного анализа
Основные понятия факторного анализа. Условия применения факторного анализа. Приемы для определения числа факторов. Обращение факторов. Использование факторного анализа в психологии.
ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
1. Измерение в психологии
2. Основные понятия математической статистики. Выборочный метод
3. Числовые характеристики распределения
4. Законы распределения
5. Оценивание и проверка гипотез.
6. Статистические критерии отличий.
7. Непараметрические критерии для связанных выборок.
8. Критерии согласия распределений и многофункциональный критерий "j"
9. Параметрические критерии отличий.
10. Дисперсионный анализ экспериментальных данных
11. Корреляционный анализ.
12. Регрессионный анализ.
13. Основы факторного анализа
РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ТИПОВЫХ ЗАДАЧ
Задание 1
Результаты, полученные в эксперименте по заучиванию ряда из xmax чисел для 100 испытуемых, предоставлены в таблицах (данные условны). Выбрав данные в соответствии со своим вариантом для признака Х выполнить следующее:
1. Выстроить данные в статистический ряд (по возрастанию);
2. Построить статистическое распределение выборки (вариационный ряд), вычислить относительные частоты;
3. Построить полигон частот. Согласно виду полигона частот выдвинуть гипотезу о законе распределения;
4. Найти эмпирическую функцию распределения и построить ее график;
5. Найти числовые характеристики меры рассеяния: вариационный размах; выборочную среднюю, дисперсию, среднее квадратичное отклонение (ошибку); стандартное отклонение; найти коэффициент вариации;
6. Найти моду, медиану; привести психологическую интерпретацию полученных результатов;
7. Отметить на полигоне частот значения выборочной средней, моды, медианы; указать какой при этом получен вид асимметрии; сделать вывод;
8. Найти выравнивающие частоты в предположении нормальности распределения; построить нормальную (теоретическую) кривую на том же рисунке, где был построен полигон частот;
9. С помощью критерия Пирсона (c2-критерия) проверить гипотезу о нормальности распределения.
| 4 | 7 | 10 | 4 | 7 | 10 | 4 | 7 | 10 | 7 | 10 | 7 |
| 7 | 10 | 7 | 13 | 10 | 7 | 10 | 13 | 10 | 7 | 7 | 10 |
| 10 | 10 | 10 | 13 | 10 | 13 | 10 | 7 | 7 | 10 | 13 | 10 |
| 16 | 13 | 10 | 7 | 13 | 10 | 16 | 16 | 7 | 10 | 16 | 19 |
| 7 | 13 | 10 | 19 | 10 | 10 | 10 | 10 | 16 | 10 | 10 | 7 |
| 7 | 7 | 10 | 7 | 10 | 13 | 10 | 13 | 13 | 10 | 13 | 13 |
| 13 | 7 | 7 | 10 | 13 | 13 | 10 | 10 | 7 | 16 | 10 | 16 |
| 10 | 10 | 13 | 10 | 10 | 10 | 10 | 10 | 7 | 10 | 10 | 7 |
| 13 | 10 | 10 | 16 |
Решение
1. Превратим данные в статистический ряд (по возрастанию)
| 4 | 4 | 4 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 10 | 10 | 10 |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| 10 | 10 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 19 | 19 |
2. Построим статистическое распределение выборки.
Статистическим распределением выборки называют перечень вариант хі и соответствующих им частот ni (сумма всех частот равняется объему выборки n) или относительных частот wi (сумма всех относительных частот равняется единице).
Построим статистическое распределение выборки. Для удобства дальнейших расчетов в таблицу добавим строки как с частотами, так и с относительными частотами.
| xi | 4 | 7 | 10 | 13 | 16 | 19 |
| ni | 3 | 24 | 45 | 18 | 8 | 2 |
| wi | 0,03 | 0,24 | 0,45 | 0,18 | 0,08 | 0,02 |
Объем выборки составляет:
n=3+24+45+18+8+2=100.
Относительные частоты рассчитываются по формуле 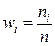
При этом выполняется: 0,03+0,24+0,45+0,18+0,08+0,02=1.
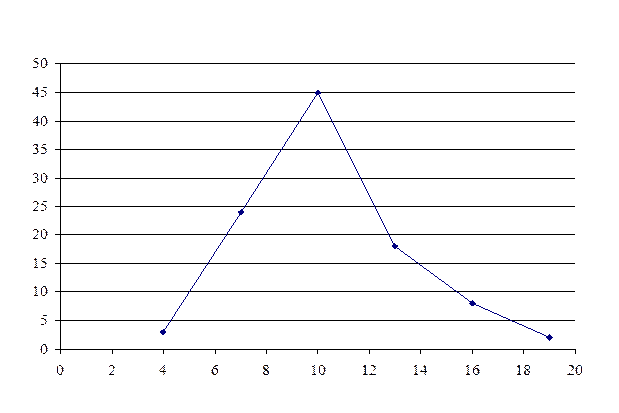
3. Построим полигон частот.
Полигоном частот называется ломаная, отрезки которой соединяют точки с координатами (x1, n1),...,( xm, nm).
|

|
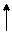
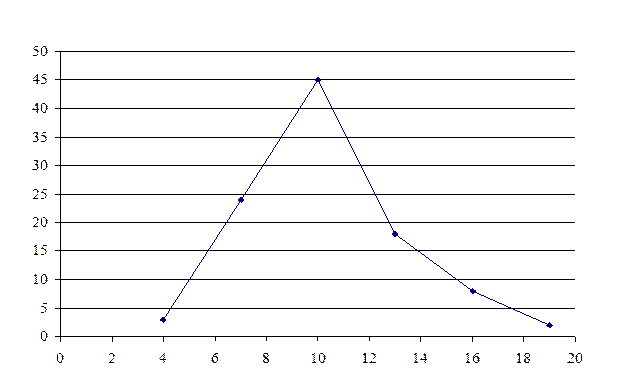
По виду полигона частот выдвинем гипотезу о нормальном законе распределения.
4. Найдем эмпирическую функцию распределения и построим ее график.
Эмпирической функцией распределения называют функцию 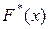 , которая определяет для каждого значения х относительную частоту события Х<х, то есть
, которая определяет для каждого значения х относительную частоту события Х<х, то есть 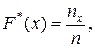 где
где 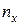 – число вариант, меньших х, n – объем выборки.
– число вариант, меньших х, n – объем выборки.
Наименьшая варианта равняется 4, значит
F*(x)=0 при 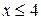 .
.
Значение Х<7, а именно х1=4, наблюдалось 3 раза, значит
F*(x)=3/100=0,03 при 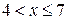 .
.
Значение Х<10, а именно х1=4 та х2=7, наблюдалось 3+24=27 раз, значит
F*(x)=27/100=0,27 при 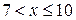 .
.
Продолжив аналогично, получим функцию распределения:
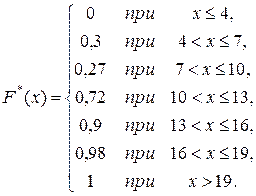
Замечание. Обратите внимание на то, что при правильных расчетах значение функции распределения при х больше самой большой варианты (в нашем случае x>19) равняется единице.
График функции распределения:






|

|

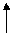
5. Найти числовые характеристики меры рассеивания, вариационный размах; выборочную среднюю, дисперсию, среднее квадратическое отклонение (ошибки); найти коэффициент вариации.
Размах вариации R=xmax-xmin
R = 19 – 4 = 15
 Найдем выборочную среднюю, дисперсию, среднее квадратическое отклонения, для этого составим расчетную таблицу:
Найдем выборочную среднюю, дисперсию, среднее квадратическое отклонения, для этого составим расчетную таблицу:
| x i | n i |
|
|
| 4 | 3 | 12 | 48 |
| 7 | 24 | 168 | 1176 |
| 10 | 45 | 450 | 4500 |
| 13 | 18 | 234 | 3042 |
| 16 | 8 | 128 | 2048 |
| 19 | 2 | 38 | 722 |
|
|
1030 |
11536 |
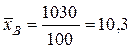
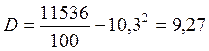
Среднее квадратическое по формуле (5):
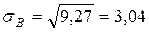
Стандартное отклонение по формуле (6):
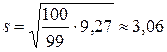
Коэффициент вариации
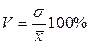
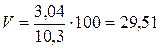
6. Найдем моду, медиану; приведем психологическую интерпретацию полученных результатов.
Мода отвечает варианте с наибольшей частотой:
Мо=10
Таким образом, среднее количество заученных чисел равняется приблизительно 10.
Медианой (Mе) называется такое значение вариационного признака, которое выпадает на середину вариационного ряда. При вычислении медианы дискретного вариационного ряда могут возникнуть два случая:
1) число вариант непарное (n=2m+1),
2) число вариант парное (n =2m).
В первом случае Me=xm+1, медиана равняется центральной (серединной) варианте ряда, это варианта с номером m=(n-1)/2;
В другом случае Me=(xm+xm+1)/2, медиана равняется полусумме, которая находится в середине ряда вариант, где n=k/2.
Основываясь на том, что n=100
m=100/2=50
Таблица 2
| i | xi | ni | Накопленные частоты |
| 1 | 4 | 3 | 3 |
| 2 | 7 | 24 | 27 |
| 3 | 10 | 45 | 72 |
| 4 | 13 | 18 | 90 |
| 5 | 16 | 8 | 98 |
Первый интервал, который превышает 50 – третий, то есть х50= х51=10.
Me=(10+10)/2=10.
Значение медианы имеет следующую интерпретацию: чуть больше двух третьих испытуемых запомнила меньше или ровно 10 слов, а вторая часть – больше 10 слов.
7. Обозначить на полигоне частот значения выборочной средней, моды, медианы; указать, какой вид асимметрии при этом получено; сделать вывод;
|
|


Если график распределения имеет правостороннюю асимметрию ("хвост" вправо), то в этом случае мода размещена левее, а среднее арифметическое – правее медианы (см. рисунок).
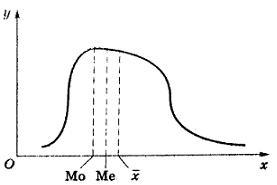
Действительно, левее и правее медианы размещены одинаковые площади, но левой части отвечает меньшая основа, а правой - большая основа. Поэтому левая часть кривой выше правой, и мода будет находиться левее медианы. По этой самой причине медиана не может служить точкой равновесия, поскольку площадь части, соответствующей большей основе, больше площади, размещенной на меньшей основе. Следовательно, среднее арифметическое находится правее медианы.
Таким образом, при правосторонней асимметрии левее расположена мода, дальше медиана и правее – среднее арифметическое. Обратное расположение имеет место при левосторонней асимметрии графика. При этом, чем более асимметричный график, тем больше расстояние между его средними точками.
В нашем случае мода размещена левее, а среднее арифметическое – правее медианы, то есть график распределения имеет правостороннюю асимметрию. Зато, разница между средним арифметическим, модой и медианой незначительна, то есть распределение приближено к нормальному.
8. Найдем выравнивающие частоты, допуская, что распределение является нормальным.
Выравнивающие (теоретические) частоты рассчитывают по формуле:
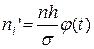 (8)
(8)
Рассчитаем теоретические частоты (смотри следующую таблицу). Для этого определим нормируемые отклонения 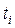 (графа 3) по формулам
(графа 3) по формулам
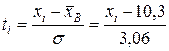 (9)
(9)
По приложению устанавливаем значение функции 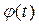 (графа 4), рассчитываем теоретические частоты по формуле (8) (графа 5):
(графа 4), рассчитываем теоретические частоты по формуле (8) (графа 5):
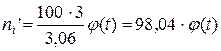
Таблица 3
| 1 | 2 | 3 | 4 | 5 |
| i | xi | ti |
|
|
| 1 | 4 | -2,06 | 0,0478 | 4,7 |
| 2 | 7 | -1,08 | 0,2227 | 21,8 |
| 3 | 10 | -0,10 | 0,397 | 38,9 |
| 4 | 13 | 0,88 | 0,2709 | 26,6 |
| 5 | 16 | 1,86 | 0,0707 | 6,9 |
| 6 | 19 | 2,84 | 0,0071 | 0,7 |
| Σ |
|
|
| 99,6 |
9. Построим на полигоне частот нормальную (теоретическую) кривую:
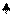
|
10. Проверим при уровне значимости 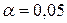 гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона.
гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона.
а) Составим расчетную таблицу (4) по которой найдем наблюдаемое
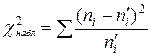 (10)
(10)
Таблица 4
| 1 | 2 | 3 | 4 | 5 | 6 |
| i |
|
|
|
|
|
| 1 | 3 | 4,7 | -1,7 | 2,8 | 0,6 |
| 2 | 24 | 21,8 | 2,2 | 4,7 | 0,2 |
| 3 | 45 | 38,9 | 6,1 | 36,9 | 0,9 |
| 4 | 18 | 26,6 | -8,6 | 73,3 | 2,8 |
| 5 | 8 | 6,9 | 1,1 | 1,1 | 0,2 |
|
| 2 | 0,7 | 1,3 | 1,7 | 2,4 |
| Σ | 100 | 99,6 | 0,4 |
|
|
Из таблицы 4 получаем 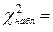 7,1.
7,1.
б) По таблице критических точек (смотри приложение 3), по уровню значимости 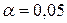 и числу степеней свободы
и числу степеней свободы 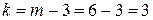 (тут m=6 – количество вариант) находим критическую точку правосторонней критичной области (табл. 3 Приложения).
(тут m=6 – количество вариант) находим критическую точку правосторонней критичной области (табл. 3 Приложения).
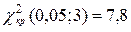
Учитывая, что 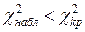 – гипотезу о нормальном распределении генеральной совокупности принимаем. То есть, эмпирические и теоретические частоты отличаются незначительно.
– гипотезу о нормальном распределении генеральной совокупности принимаем. То есть, эмпирические и теоретические частоты отличаются незначительно.
Задание 2
Проведены две серии испытаний по измерению пространственных порогов тактильной чувствительности (в мм). Данные, полученные в первой серии испытаний, представлены в таблицах в соответствии с Вашим вариантом. Данные, полученные во второй серии, представлены в таблице следующего варианта.
Способствовала ли корректирующая работа увеличению порогов тактильной чувствительности?
Решить задание двумя способами:
1) с помощью критерия знаков;
2) с помощью статистического критерия T-Вилкоксона.
Первая серия исследований
| 31 | 30 | 27 | 30 | 32 | 36 | 28 | 27 |
| 36 | 31 | 39 | 35 | 29 | 34 | 38 | 35 |
Вторая серия исследований
| 35 | 32 | 38 | 34 | 28 | 37 | 33 | 31 |
| 31 | 30 | 27 | 30 | 32 | 36 | 28 | 27 |
Решение
Выдвигаем статистические гипотезы:
Н0 – отличия в тактильной чувствительности до и после корректирующей работы несущественны;
Н1 – отличия существенны.
1) Выясним с помощью критерия знаков, способствовала ли корректирующая работа увеличению порогов тактильной чувствительности.
Составим расчетную таблицу:
| № испытуемого | Уровень тактильной чувствительности «до» корректирующей работы (1 серия испытаний) | Уровень тактильной чувствительности «после» корректирующей работы (2 серия испытаний) | Сдвиг |
| 1 | 31 | 35 | + 4 |
| 2 | 30 | 32 | + 2 |
| 3 | 27 | 38 | + 11 |
| 4 | 30 | 34 | + 4 |
| 5 | 32 | 28 | – 4 |
| 6 | 36 | 37 | + 1 |
| 7 | 28 | 33 | + 5 |
| 8 | 27 | 31 | + 4 |
| 9 | 36 | 31 | – 5 |
| 10 | 31 | 30 | – 1 |
| 11 | 39 | 27 | – 12 |
| 12 | 35 | 30 | – 5 |
| 13 | 29 | 32 | + 3 |
| 14 | 34 | 36 | + 2 |
| 15 | 38 | 28 | – 10 |
| 16 | 35 | 27 | – 8 |
Общее количество нулевых сдвигов – 0;
Типичный сдвиг (в этом случае – положительный) 9;
Нетипичный сдвиг (в этом случае – отрицательный) Gэмп=7.
По таблице 4 приложения определяем критические значения G-критерия при уровнях значимости Р=0,05 и Р=0,01 и количество сдвигов (сумма типичных и нетипичных) n=9+7=16. Получаем:
| n | Р | |
| 0,05 | 0,01 | |
| 16 | 4 | 2 |
Ось значимости:
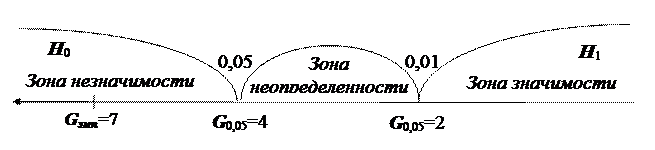
Gэмп попало в зону незначимости, значит принимается гипотеза Н0, то есть корректирующая работа не привела к существенным изменениям в порогах тактильной чувствительности.
2) Выясним с помощью статистического критерия T-Вилкоксона, повлияла ли корректирующая работа на увеличение порогов тактильной чувствительности.
| № п/п | "До" | "После" | Сдвиг | Абсолютный сдвиг | Ранг абсолютного сдвига |
| 1 | 31 | 35 | + 4 | 4 | 7,5 |
| 2 | 30 | 32 | + 2 | 2 | 3,5 |
| 3 | 27 | 38 | + 11 | 11 | 15 |
| 4 | 30 | 34 | + 4 | 4 | 7,5 |
| 5 | 32 | 28 | – 4 | 4 | 7,5 |
| 6 | 36 | 37 | +1 | 1 | 1,5 |
| 7 | 28 | 33 | + 5 | 5 | 11 |
| 8 | 27 | 31 | + 4 | 4 | 7,5 |
| 9 | 36 | 31 | – 5 | 5 | 11 |
| 10 | 31 | 30 | – 1 | 1 | 1,5 |
| 11 | 39 | 27 | – 12 | 12 | 16 |
| 12 | 35 | 30 | – 5 | 5 | 11 |
| 13 | 29 | 32 | + 3 | 3 | 5 |
| 14 | 34 | 36 | + 2 | 2 | 3,5 |
| 15 | 38 | 28 | – 10 | 10 | 14 |
| 16 | 35 | 27 | – 8 | 8 | 13 |
Столбец "Сдвиг" находят как разницу столбца "после" и столбца "до". В столбец "абсолютный сдвиг" переписываем числа из столбца "сдвиг" без знаков. В столбце "ранг абсолютного сдвига" минимальному из элементов (в данном случае это 1) нужно предоставить ранг 1. Однако, в нашем примере таких чисел два, они занимают 1 и 2 порядковые места, им приписывают усредненный ранг (1+2)/2=1,5 Следующий по величине абсолютный сдвиг 2 встречается также дважды, они занимают 3 и 4 порядковые места, им приписывают ранг (3+4) /2=3,5 и так далее.
Тэмп численно равняется сумме рангов нетипичных сдвигов. В нашем случае нетипичных сдвигов семь (это все отрицательные значения сдвигов). Сумма их рангов равняется:
Тэмп =7,5+11+1,5+16+11+14+13=74.
Далее оценка статистической достоверности сдвига по критерию проводиться по таблице 5 (смотри Приложение). Поиск критических величин по таблице проводится по количеству испытуемых. В нашем случае n=16, потому часть таблицы выглядит так:
| n | Р | |
| 0,05 | 0,01 | |
| 16 | 35 | 23 |
Ось значимости: 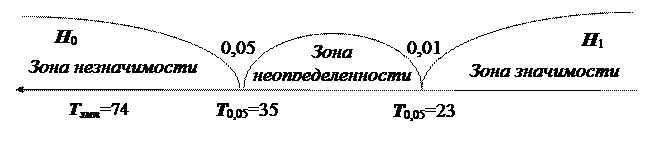
Темп попало в зону незначимости, значит принимается гипотеза Н0, то есть корректирующая работа не повлияла на существенное увеличение порогов тактильной чувствительности.
Задание 3
При измерении пространственных порогов тактильной чувствительности получены следующие величины порогов для женщин (данные представлены в таблице в соответствии с Вашим вариантом) и мужчин (данные представлены в таблице следующего варианта).
Необходимо:
1) статистические данные, полученные в результате эксперимента (отдельно для женщин и мужчин) представить в виде статистического ряда, рассчитать их среднее выборочное, ошибки средних, среднее выборочное квадратичное отклонение;
2) с помощью критерия Стьюдента выяснить, являются ли статистически значимыми отличия между средними значениями двух выборок;
3) с помощью критерия числа инверсий (U-Вилкоксона-Манна-Уитни) выяснить, будут ли статистически достоверными отличия между величинами порогов тактильной чувствительности у женщин и мужчин.
Сделайте выводы о наличии (или отсутствие) существенной разницы между уровнями порогов тактильной чувствительности женщин и мужчин.
Пороги тактильной чувствительности у женщин (мм) (Распределение X)
| 31 | 30 | 27 | 30 | 32 | 36 | 28 | 27 |
| 36 | 31 | 39 | 35 | 29 | 34 | 38 | 35 |
Пороги тактильной чувствительности у мужчин (мм) (Распределение Y)
| 35 | 32 | 38 | 34 | 28 | 37 | 33 | 31 |
| 31 | 30 | 27 | 30 | 32 | 36 | 28 | 27 |
Решение
1) Распределение X (пороги тактильной чувствительности у женщин)
Статистический ряд
| хi | 27 | 28 | 29 | 30 | 31 | 32 | 34 | 35 | 36 | 38 | 39 |
| ni | 2 | 1 | 1 | 2 | 2 | 1 | 1 | 2 | 2 | 1 | 1 |
Объем выборки n=16
Среднее выборочное
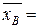 (27×2+28+29+30×2+31×2+32+34+35×2+36×2+38+39)/16=32,38
(27×2+28+29+30×2+31×2+32+34+35×2+36×2+38+39)/16=32,38
Дисперсия
D(X)= (2×272+282+292+302×2+312×2+322+342+352×2+362×2+382+392)/16–32,382=13,9
Среднее выборочное квадратическое отклонение
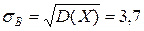
Ошибка средней определяется по формуле: 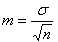 m=3,7/4=0,9
m=3,7/4=0,9
1) Распределение Y (пороги тактильной чувствительности у мужчин)
Статистический ряд
| yj | 27 | 28 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
| nj | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
Объем выборки n=16
Среднее выборочное
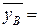 31,81
31,81
Дисперсия
D(Y)=11,4
Среднее выборочное квадратическое отклонение
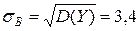
Ошибка средней определяется по формуле: 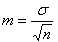 m=3,4/4=0,84
m=3,4/4=0,84
2) С помощью критерия Стьюдента выясним, являются ли статистически значимыми отличия между средними значениями двух выборок.
Вычислим эмпирическое значение критической статистики
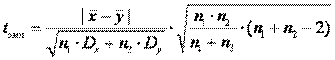
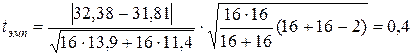
Примем уровень значимости a=0,01.
Определим по таблице критическое значение 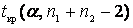 для соответствующего уровня значимости и данного числа степеней свободы
для соответствующего уровня значимости и данного числа степеней свободы 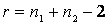 т.е. r=16+16-2=30. То есть,
т.е. r=16+16-2=30. То есть, 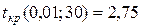 .
.
tэмп=0,4 < 2,75=tкр(0,01;30), то есть, гипотеза о несущественности отличий средних значений пространственных порогов тактильной чувствительности на уровне значимости α=0,01 принимается.
Можно говорить о приблизительно одинаковом уровне чувствительности у женщин и мужчин.
3) С помощью критерия числа инверсий (U- Вилкоксона-Манна-Уитни) выясни, будут ли статистически достоверными отличия между величинами порогов тактильной чувствительности у женщин и мужчин;
Сформулируем статистические гипотезы:
Н0 – отсутствуют статистически достоверные отличия между величинами порогов тактильной чувствительности у женщин и мужчин;
Н1 –имеются статистически достоверные отличия между величинами порогов тактильной чувствительности у женщин и мужчин.
Представим ряд в виде таблицы, в которую прибавлены еще два столбца для подсчета инверсий (табл.5)
Инверсии X/Y подсчитываются таким образом: число 27 первого столбца не имеет перед собой ни одного числа второго столбца, поэтому в третьем столбце напротив 27 пишем ноль; число 28 первого столбца имеют перед собой 2 числа второго столбца (27, 27), потому в третьем столбце напротив 28 ставим 2. И так далее. Таким образом, суммарное число инверсий X/Y третьего столбца равняется 126. То есть U (X/Y) =126.
Аналогичным способом подсчитывают суммарное число инверсий Y/X четвертого столбца, который равняется 108, U (Y/X) =108.
Таблица 5
| X | Y | Инверсия X/Y | Инверсия Y/X |
| 27 | 27 | 0 | 0 |
| 27 | 27 | 0 | 0 |
| 28 | 28 | 2 | 2 |
|
| 28 |
| 2 |
| 29 |
| 4 |
|
| 30 | 30 | 4 | 4 |
| 30 | 30 | 4 | 4 |
| 31 | 31 | 6 | 6 |
| 31 | 31 | 6 | 6 |
| 32 | 32 | 8 | 8 |
|
| 32 |
| 8 |
|
| 33 |
| 9 |
| 34 | 34 | 11 | 9 |
| 35 | 35 | 12 | 10 |
| 35 |
| 12 |
|
| 36 | 36 | 13 | 12 |
| 36 |
| 13 |
|
|
| 37 |
| 14 |
| 38 | 38 | 15 | 14 |
| 39 |
| 16 |
|
| Суммы инверсий | 126 | 108 | |
Считают, что Uэмп минимальная из сумм инверсий. Имеем Uэмп=108.
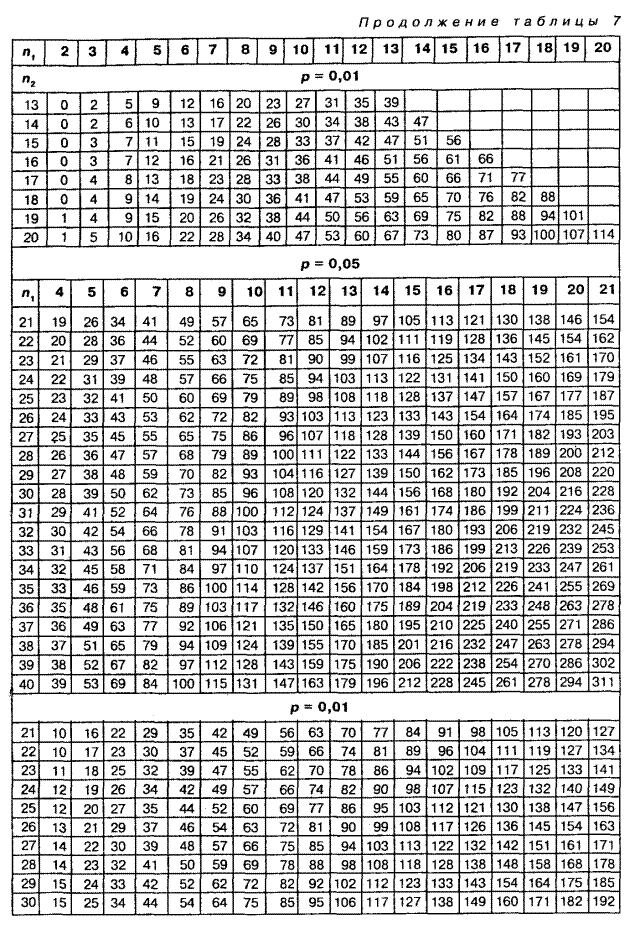
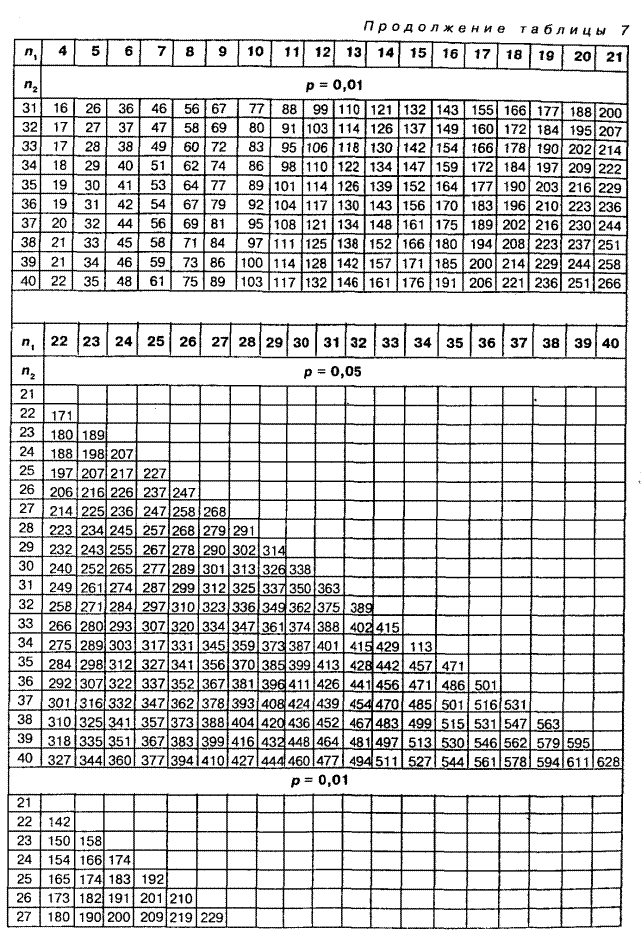
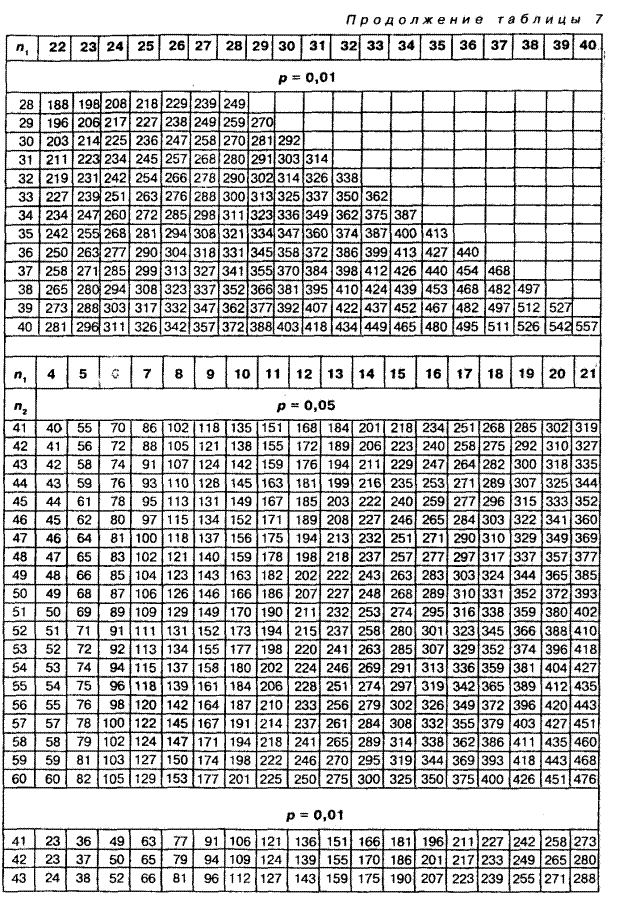
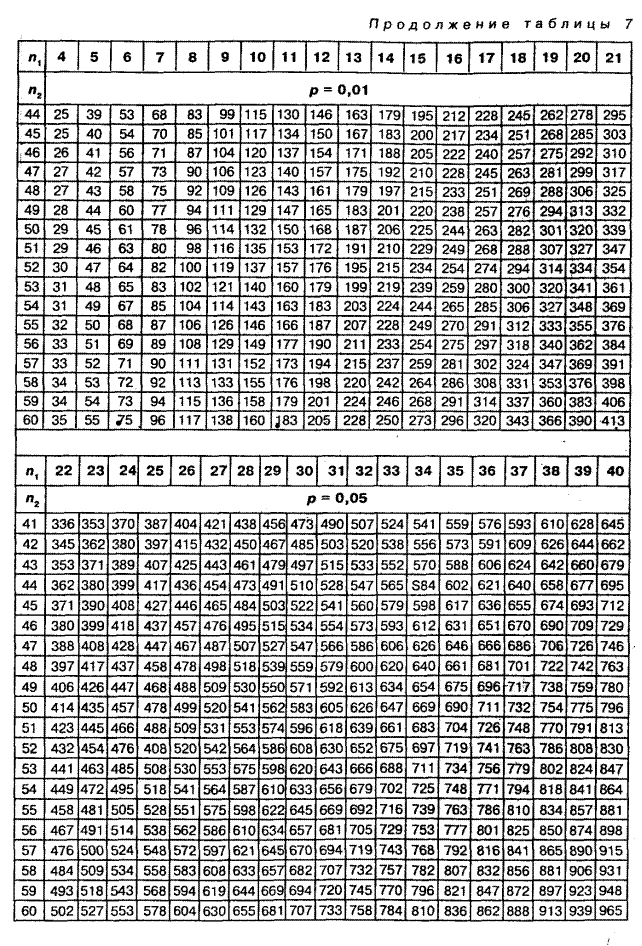
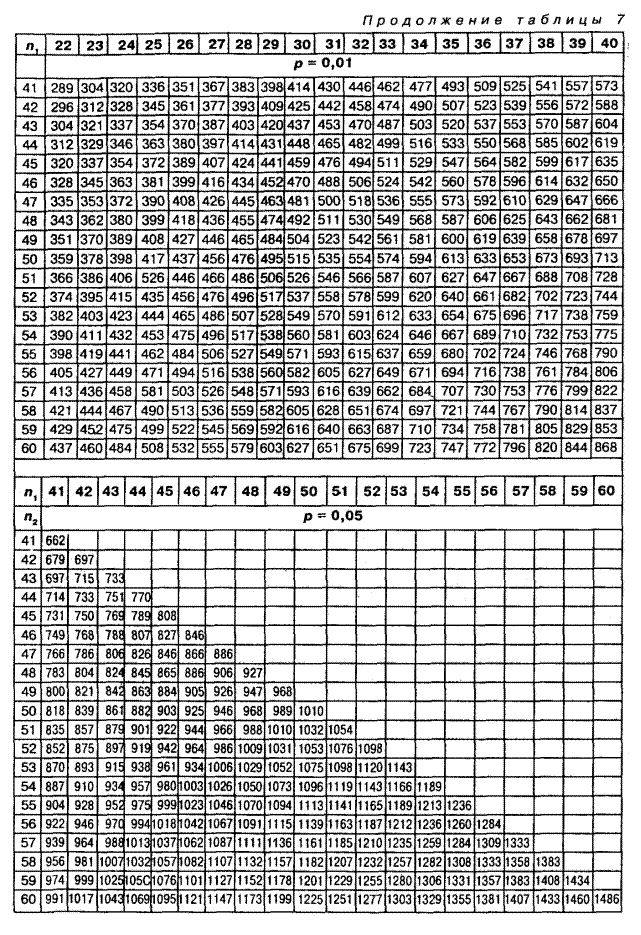
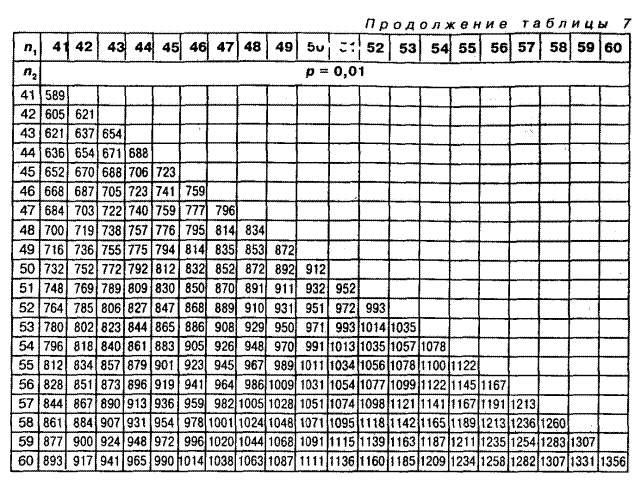
По таблице 7 Приложения определяем критическое значение U-критерия при уровнях значимости Р=0,05 и Р=0,01 и количеством испытуемых n1=16 и n2=16. Получаем:
| n1/ n2 | Р | |
| 0,05 | 0,01 | |
| 16/16 | 83 | 66 |
Ось значимости: 
Uэмп попало в зону незначимости, следовательно принимается гипотеза Н0, то есть отсутствуют статистически достоверные отличия между величинами порогов тактильной чувствительности у женщин и мужчин.
Задание 4
Предоставлены данные, которые характеризуют зависимость признака Y (объем непроизвольного запоминания) от признака Х (объем запоминания после первого предъявления в эксперименте по заучиванию двузначных чисел). На основе этих данных:
- построить корреляционное поле;
- вычислить выборочный коэффициент корреляции;
- найти выборочное уравнение линейной регрессии, которое описывает корреляционную зависимость Y от Х. Нанести полученное уравнение на корреляционное поле.
| Y | Х | |||||
| 2 | 3 | 4 | 5 | 6 | 7 | |
| 4 | 1 | 8 | – | – | – | – |
| 5 | – | 9 | 3 | – | – | – |
| 6 | – | 4 | 5 | 46 | – | – |
| 7 | – | – | – | 6 | 8 | – |
| 8 | – | – | – | – | 4 | 6 |
Решение.
Построим корреляционное поле:
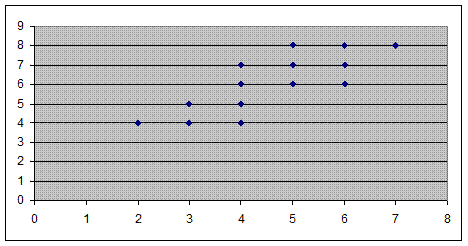
Составим расчетную таблицу:
Таблица 6
| Y | Х | nyі |
|
|
| nxyXY | |||||
| 2 | 3 | 4 | 5 | 6 | 7 | ||||||
| 4 | 1 | 8 | – | – | – | – | 9 | 36 | 16 | 144 | 104 |
| 5 | – | 9 | 3 | – | – | – | 12 | 60 | 25 | 300 | 195 |
| 6 | – | 4 | 5 | 46 | – | – | 55 | 330 | 36 | 1980 | 1572 |
| 7 | – | – | – | 6 | 8 | – | 14 | 98 | 49 | 686 | 546 |
| 8 | – | – | – | – | 4 | 6 | 10 | 80 | 64 | 640 | 528 |
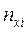
| 1 | 21 | 8 | 52 | 12 | 6 | 100 | 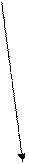 604 604
| 190 | 3750 | 2945 |
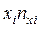
| 2 | 63 |  32 32
| 260 | 72 | 42 | 471 | ||||
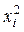
| 4 | 9 | 16 | 25 | 36 | 49 | 139 | ||||
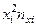
| 4 | 189 | 128 | 1300 | 432 | 294 | 2347 | ||||
| nxyXY | 8 | 303 | 180 | 1590 | 528 | 336 | 2945 | ||||
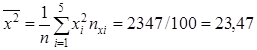
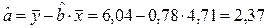
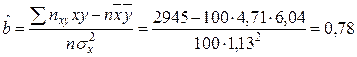
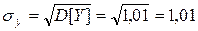
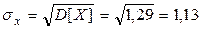
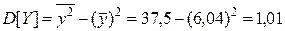
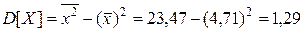
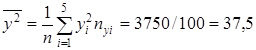
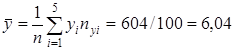
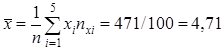
Значит, уравнение линейной регрессии имеет вид:
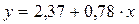
Выборочный коэффициент корреляции:
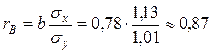 |
То есть, связь между признаком Y (объемом непроизвольного запоминания) и признаком Х (объемом запоминания после первого предъявления в эксперименте по заучиванию двузначных чисел) очень тесна.
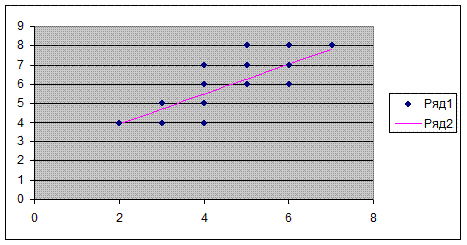
Нанесем полученное уравнение на корреляционное поле:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Задание 1
Результаты, полученные в эксперименте по заучиванию ряда из xmax чисел для 100 испытуемых, предоставлены в таблицах (данные условны). Выбрав данные в соответствии со своим вариантом для признака Х выполнить следующее:
1. Превратить данные в статистический ряд (по возрастанию);
2. Построить статистическое распределение выборки (вариационный ряд), вычислить относительные частоты;
3. Построить полигон частот. Согласно виду полигона частот выдвинуть гипотезу о законе распределения;
4. Найти эмпирическую функцию распределения и построить ее график;
5. Найти числовые характеристики меры рассеяния: вариационный размах; выборочную среднюю, дисперсию, среднее квадратичное отклонение (ошибку); стандартное отклонение; найти коэффициент вариации;
6. Найти моду, медиану; привести психологическую интерпретацию полученных результатов;
7. Отметить на полигоне частот значения выборочной средней, моды, медианы; указать какой при этом получен вид асимметрии; сделать вывод;
8. Построить доверительный интервал с надежностью 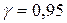 для оценки математической надежды при известном
для оценки математической надежды при известном 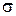 (принятое
(принятое 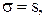 распределение считать нормальным);
распределение считать нормальным);
9. Найти выравнивающие частоты в предположении нормальности распределения; построить нормальную (теоретическую) кривую на том же рисунке, где был построен полигон частот;
10. С помощью критерия Пирсона (c2-критерия) проверить гипотезу о нормальности распределения.
Вариант 1
| 40 | 100 | 30 | 60 | 40 | 70 | 40 | 80 | 20 | 50 | 70 | 30 |
| 60 | 40 | 70 | 50 | 40 | 70 | 60 | 30 | 50 | 60 | 50 | 60 |
| 90 | 30 | 50 | 60 | 40 | 80 | 50 | 60 | 70 | 60 | 20 | 90 |
| 60 | 80 | 60 | 50 | 30 | 40 | 70 | 40 | 50 | 60 | 10 | 50 |
| 60 | 50 | 40 | 60 | 50 | 90 | 60 | 40 | 80 | 50 | 70 | 60 |
| 60 | 70 | 20 | 70 | 40 | 60 | 40 | 80 | 30 | 70 | 60 | 80 |
| 30 | 50 | 60 | 50 | 60 | 80 | 20 | 30 | 30 | 50 | 70 | 40 |
| 30 | 60 | 50 | 60 | 50 | 60 | 20 | 60 | 50 | 70 | 40 | 100 |
| 50 | 60 | 40 | 50 |
Вариант 2
| 14 | 16 | 8 | 18 | 10 | 18 | 20 | 12 | 18 | 22 | 10 | 8 |
| 16 | 14 | 18 | 14 | 20 | 14 | 20 | 10 | 10 | 24 | 12 | 26 |
| 14 | 22 | 10 | 22 | 12 | 16 | 24 | 18 | 20 | 12 | 20 | 26 |
| 16 | 12 | 16 | 14 | 18 | 14 | 18 | 16 | 18 | 14 | 20 | 14 |
| 18 | 20 | 14 | 16 | 10 | 20 | 22 | 14 | 26 | 22 | 20 | 16 |
| 12 | 24 | 14 | 18 | 12 | 18 | 16 | 10 | 16 | 14 | 22 | 18 |
| 22 | 14 | 16 | 24 | 20 | 14 | 20 | 10 | 16 | 10 | 18 | 14 |
| 16 | 22 | 14 | 18 | 12 | 16 | 14 | 10 | 20 | 16 | 22 | 14 |
| 20 | 16 | 14 | 18 |
Вариант 3
| 46 | 52 | 58 | 34 | 52 | 40 | 58 | 22 | 52 | 46 | 40 | 58 |
| 28 | 52 | 40 | 34 | 52 | 40 | 52 | 46 | 40 | 58 | 22 | 64 |
| 40 | 28 | 46 | 46 | 40 | 34 | 52 | 40 | 52 | 34 | 46 | 64 |
| 46 | 58 | 40 | 58 | 28 | 46 | 58 | 46 | 52 | 58 | 40 | 58 |
| 28 | 52 | 70 | 46 | 64 | 46 | 58 | 34 | 70 | 58 | 64 | 34 |
| 40 | 52 | 64 | 34 | 46 | 64 | 52 | 46 | 52 | 70 | 40 | 52 |
| 64 | 46 | 70 | 46 | 70 | 34 | 46 | 28 | 34 | 64 | 46 | 46 |
| 76 | 52 | 70 | 34 | 58 | 40 | 52 | 64 | 46 | 64 | 76 | 46 |
| 76 | 58 | 70 | 40 |
Вариант 4
| 2 | 17 | 8 | 26 | 11 | 11 | 26 | 14 | 11 | 14 | 17 | 8 |
| 23 | 8 | 17 | 14 | 20 | 11 | 20 | 11 | 5 | 14 | 14 | 17 |
| 8 | 17 | 23 | 29 | 5 | 14 | 11 | 11 | 14 | 17 | 20 | 17 |
| 20 | 17 | 20 | 11 | 8 | 14 | 8 | 14 | 5 | 14 | 23 | 14 |
| 11 | 14 | 11 | 5 | 17 | 23 | 29 | 29 | 17 | 11 | 17 | 11 |
| 14 | 11 | 20 | 2 | 20 | 17 | 20 | 8 | 14 | 8 | 8 | 14 |
| 23 | 20 | 17 | 17 | 11 | 17 | 8 | 23 | 14 | 23 | 20 | 26 |
| 14 | 11 | 8 | 14 | 11 | 26 | 14 | 26 | 14 | 20 | 11 | 5 |
| 11 | 8 | 5 | 23 |
Вариант 5
| 65 | 90 | 85 | 75 | 75 | 90 | 75 | 90 | 105 | 80 | 80 | 85 |
| 70 | 80 | 105 | 75 | 95 | 95 | 100 | 75 | 85 | 75 | 80 | 75 |
| 100 | 70 | 85 | 100 | 95 | 75 | 80 | 95 | 75 | 80 | 95 | 85 |
| 75 | 90 | 100 | 75 | 75 | 90 | 75 | 80 | 90 | 85 | 75 | 85 |
| 90 | 70 | 75 | 100 | 80 | 105 | 105 | 95 | 85 | 90 | 75 | 80 |
| 80 | 70 | 95 | 110 | 75 | 75 | 100 | 75 | 75 | 110 | 85 | 80 |
| 105 | 100 | 90 | 75 | 105 | 85 | 80 | 110 | 85 | 75 | 80 | 95 |
| 75 | 75 | 85 | 95 | 110 | 100 | 95 | 100 | 90 | 85 | 80 | 75 |
| 80 | 70 | 90 | 65 |
Вариант 6
| 30 | 55 | 50 | 60 | 50 | 55 | 45 | 75 | 40 | 40 | 45 | 55 |
| 50 | 60 | 50 | 35 | 50 | 45 | 50 | 70 | 50 | 55 | 35 | 65 |
| 45 | 45 | 65 | 45 | 50 | 60 | 40 | 40 | 55 | 55 | 50 | 50 |
| 55 | 50 | 60 | 45 | 30 | 45 | 55 | 35 | 55 | 55 | 40 | 55 |
| 60 | 30 | 50 | 35 | 55 | 50 | 50 | 55 | 60 | 50 | 55 | 65 |
| 45 | 55 | 55 | 45 | 45 | 55 | 50 | 35 | 60 | 50 | 50 | 65 |
| 50 | 70 | 75 | 30 | 45 | 65 | 50 | 35 | 55 | 65 | 40 | 70 |
| 50 | 50 | 45 | 70 | 55 | 70 | 65 | 60 | 50 | 50 | 45 | 40 |
| 55 | 45 | 40 | 50 |
Вариант 7
| 1 | 22 | 36 | 29 | 15 | 36 | 22 | 36 | 8 | 29 | 22 | 29 |
| 29 | 36 | 8 | 36 | 29 | 22 | 29 | 15 | 36 | 50 | 43 | 29 |
| 29 | 43 | 22 | 43 | 29 | 50 | 15 | 36 | 15 | 43 | 22 | 36 |
| 50 | 8 | 29 | 22 | 8 | 22 | 50 | 22 | 29 | 29 | 29 | 36 |
| 15 | 29 | 36 | 22 | 43 | 15 | 50 | 22 | 43 | 29 | 50 | 29 |
| 57 | 22 | 15 | 43 | 36 | 15 | 36 | 43 | 29 | 22 | 50 | 36 |
| 1 | 29 | 43 | 8 | 57 | 22 | 43 | 15 | 22 | 29 | 36 | 22 |
| 15 | 29 | 43 | 22 | 15 | 29 | 29 | 22 | 43 | 15 | 36 | 64 |
| 22 | 36 | 15 | 57 |
Вариант 8
| 13 | 29 | 21 | 29 | 37 | 45 | 37 | 29 | 29 | 21 | 29 | 45 |
| 37 | 29 | 37 | 5 | 45 | 37 | 29 | 13 | 29 | 29 | 45 | 53 |
| 37 | 29 | 69 | 21 | 37 | 5 | 13 | 29 | 61 | 29 | 53 | 29 |
| 61 | 45 | 61 | 37 | 45 | 69 | 29 | 37 | 21 | 61 | 45 | 61 |
| 21 | 37 | 29 | 45 | 37 | 29 | 29 | 29 | 21 | 53 | 29 | 45 |
| 5 | 69 | 21 | 77 | 53 | 45 | 29 | 13 | 37 | 13 | 21 | 29 |
| 45 | 37 | 13 | 37 | 69 | 53 | 21 | 61 | 21 | 29 | 37 | 21 |
| 53 | 29 | 37 | 21 | 13 | 29 | 29 | 21 | 53 | 53 | 37 | 69 |
| 29 | 61 | 21 | 69 |
Вариант 9
| 16 | 22 | 22 | 19 | 16 | 34 | 31 | 28 | 25 | 19 | 25 | 13 |
| 13 | 22 | 19 | 37 | 28 | 28 | 31 | 34 | 25 | 16 | 34 | 19 |
| 22 | 25 | 28 | 22 | 31 | 16 | 22 | 34 | 16 | 31 | 28 | 31 |
| 28 | 25 | 19 | 31 | 22 | 31 | 19 | 25 | 22 | 19 | 22 | 25 |
| 22 | 25 | 16 | 28 | 37 | 28 | 31 | 16 | 16 | 25 | 25 | 25 |
| 22 | 28 | 34 | 34 | 34 | 22 | 19 | 28 | 31 | 13 | 34 | 28 |
| 22 | 28 | 28 | 22 | 13 | 28 | 19 | 25 | 19 | 25 | 25 | 31 |
| 25 | 28 | 22 | 31 | 28 | 37 | 22 | 31 | 19 | 25 | 19 | 10 |
| 31 | 25 | 25 | 10 |
Вариант 10
| 40 | 44 | 32 | 52 | 44 | 36 | 44 | 52 | 32 | 48 | 40 | 44 |
| 40 | 36 | 48 | 40 | 32 | 40 | 44 | 28 | 36 | 56 | 48 | 40 |
| 48 | 40 | 60 | 36 | 52 | 40 | 44 | 52 | 32 | 40 | 52 | 44 |
| 48 | 36 | 56 | 40 | 44 | 56 | 40 | 52 | 28 | 48 | 48 | 40 |
| 44 | 52 | 32 | 48 | 52 | 44 | 56 | 36 | 52 | 40 | 52 | 48 |
| 56 | 32 | 60 | 44 | 56 | 48 | 60 | 36 | 44 | 52 | 40 | 48 |
| 52 | 32 | 60 | 48 | 56 | 44 | 48 | 32 | 40 | 56 | 36 | 60 |
| 40 | 44 | 52 | 44 | 36 | 48 | 44 | 40 | 64 | 48 | 60 | 36 |
| 64 | 44 | 60 | 40 |
Задание 2
Проведены две серии испытаний по измерению пространственных порогов тактильной чувствительности (в мм). Данные, полученные в первой серии испытаний, представлены в таблицах в соответствии с Вашим вариантом. Данные, полученные во второй серии, представлены в таблице следующего варианта.
Способствовала ли корректирующая работа увеличению порогов тактильной чувствительности?
Решить задание двумя способами:
1) с помощью критерия знаков;
2) с помощью статистического критерия T-Вилкоксона.
Вариант 1
| 31 | 30 | 27 | 30 | 32 | 36 | 28 | 27 |
| 36 | 31 | 39 | 35 | 29 | 34 | 38 | 35 |
Вариант 2
| 35 | 32 | 38 | 34 | 28 | 37 | 33 | 31 |
| 31 | 30 | 27 | 30 | 32 | 36 | 28 | 27 |
Вариант 3
| 32 | 28 | 31 | 33 | 31 | 37 | 28 | 29 |
| 29 | 34 | 38 | 35 | 36 | 31 | 39 | 35 |
Вариант 4
| 37 | 27 | 34 | 30 | 33 | 34 | 29 | 31 |
| 38 | 35 | 29 | 34 | 39 | 35 | 36 | 31 |
Вариант 5
| 32 | 36 | 27 | 30 | 31 | 35 | 28 | 27 |
| 33 | 34 | 29 | 31 | 37 | 27 | 34 | 30 |
Вариант 6
| 26 | 27 | 26 | 34 | 29 | 30 | 33 | 28 |
| 29 | 34 | 36 | 26 | 27 | 33 | 30 | 25 |
Вариант 7
| 26 | 27 | 29 | 34 | 36 | 33 | 30 | 25 |
| 26 | 34 | 29 | 26 | 27 | 26 | 33 | 35 |
Вариант 8
| 29 | 26 | 27 | 26 | 33 | 35 | 26 | 34 |
| 27 | 29 | 34 | 36 | 26 | 33 | 27 | 32 |
Вариант 9
| 31 | 30 | 27 | 30 | 32 | 36 | 28 | 27 |
| 27 | 29 | 34 | 36 | 26 | 33 | 27 | 32 |
Вариант 10
| 32 | 36 | 27 | 30 | 31 | 35 | 28 | 27 |
| 29 | 26 | 27 | 26 | 33 | 35 | 26 | 34 |
Задание 3
При измерении пространственных порогов тактильной чувствительности получены следующие величины порогов для женщин (данные представлены в таблице в соответствии с Вашим вариантом) и мужчин (данные представлены в таблице следующего варианта).
Необходимо:
1) статистические данные, полученные в результате эксперимента (отдельно для женщин и мужчин) представить в виде статистического ряда, рассчитать их среднее выборочное, ошибки средних, среднее выборочное квадратичное отклонение;
2) с помощью критерия Стьюдента выяснить, являются ли статистически значимыми отличия между средними значениями двух выборок;
3) с помощью критерия числа инверсий (U- Вилкоксона-Манна-Уитни) выяснить, будут ли статистически достоверными отличия между величинами порогов тактильной чувствительности у женщин и мужчин;
Сделайте выводы о наличии (или отсутствие) существенной разницы между уровнями порогов тактильной чувствительности женщин и мужчин.
Задание 4
Предоставлены данные, которые характеризуют зависимость признака Y (объем непроизвольного запоминания) от признака Х (объем запоминания после первого предъявления в эксперименте по заучиванию двузначных чисел). На основе этих данных:
– построить корреляционное поле;
– вычислить выборочный коэффициент корреляции;
– найти выборочное уравнение линейной регрессии, которое описывает корреляционную зависимость Y от Х. Нанести полученное уравнение на корреляционное поле.
| 1. | 2. | |||||||||||||
| Y | Х | Y | Х | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 4 | 1 | 8 | - | - | - | - | 4 | 8 | 3 | 4 | - | - | - | |
| 5 | - | 9 | 3 | - | - | - | 5 | - | - | 11 | 38 | - | - | |
| 6 | - | 4 | 5 | 46 | - | - | 6 | - | - | 6 | 1 | 4 | - | |
| 7 | - | - | - | 6 | 8 | - | 7 | - | - | - | 7 | 1 | - | |
| 8 | - | - | - | - | 4 | 6 | 8 | - | - | - | - | 9 | 8 | |
| 3. | 4. | |||||||||||||
| Y | Х | Y | Х | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 4 | 3 | 5 | 4 | - | - | - | 4 | 1 | 3 | 6 | - | - | - | |
| 5 | - | 2 | 1 | 3 | - | - | 5 | - | 4 | 7 | - | - | - | |
| 6 | - | 4 | 40 | 8 | - | - | 6 | - | - | 50 | 9 | 1- | - | |
| 7 | - | - | - | 5 | 7 | 5 | 7 | - | - | 2 | 8 | 2 | - | |
| 8 | - | - | - | - | 7 | 10 | 8 | - | - | - | 1 | 3 | 3 | |
| 5. | 6. | |||||||||||||
| Y | Х | Y | Х | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 4 | 4 | 1 | 3 | - | - | - | 4 | 3 | 5 | - | - | - | - | |
| 5 | - | 6 | 11 | - | - | - | 5 | - | 15 | 9 | - | - | - | |
| 6 | - | 2 | 1 | 52 | - | - | 6 | - | - | 23 | 6 | 1 | - | |
| 7 | - | - | - | 5 | 6 | - | 7 | - | - | - | 12 | 7 | - | |
| 8 | - | - | - | - | 3 | 6 | 8 | - | - | - | - | 14 | 5 | |
| 7. | 8. | |||||||||||||
| Y | Х | Y | Х | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 4 | 1 | 4 | - | - | - | - | 4 | 4 | 1 | 3 | - | - | - | |
| 5 | - | 5 | 9 | - | - | - | 5 | - | 5 | 6 | - | - | - | |
| 6 | - | - | 38 | 6 | 9- | - | 6 | - | - | 7 | 40 | 8 | - | |
| 7 | - | - | 4 | 3 | 10 | - | 7 | - | - | - | 9 | 1 | 3 | |
| 8 | - | - | - | - | 1 | 10 | 8 | - | - | - | - | 9 | 4 | |
| 9. | 10. | |||||||||||||
| Y | Х | Y | Х | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 4 | 2 | 2 | 3 | - | - | - | 4 | 7 | 33 | - | - | - | - | |
| 5 | - | 4 | 4 | 5 | - | - | 5 | - | - | 12 | 5 | - | - | |
| 6 | - | - | 40 | 11 | 21 | - | 6 | - | - | - | 7 | 8 | - | |
| 7 | - | - | - | 1 | 2 | 1 | 7 | - | - | - | 9 | 11 | 1 | |
| 8 | - | - | - | - | - | 4 | 8 | - | - | - | - | 2 | 5 | |
ПРИЛОЖЕНИЯ
Таблица 1. Значение функции Лапласа 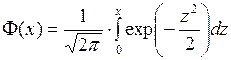
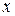
| 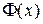
| 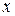
| 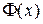
| 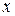
| 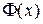
| 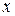
| 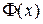
| 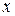
| 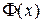
| 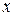
| 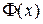
|
| 0,00 01 02 03 04 05 06 07 08 09 0,10 11 12 13 14 15 16 17 18 19 0,20 21 22 23 24 25 26 27 28 29 0,30 31 32 33 34 35 36 37 38 39 | 0,00000 00399 00798 01197 01595 01994 02392 02790 03188 03586 03983 04380 04776 05172 05567 05962 06356 06749 07142 07535 07926 08317 08706 09095 09483 09871 10257 10642 11026 11409 11791 12172 12552 12930 13307 13683 14058 14431 14803 15173 | 0,40 41 42 43 44 45 46 47 48 49 0,50 51 52 53 54 55 56 57 58 59 0,60 61 62 63 64 65 66 67 68 69 0,70 71 72 73 74 75 76 77 78 79 | 0,15542 15910 16276 16640 17003 17364 17724 18082 18439 18793 19146 19497 19847 20194 20540 20884 21226 21566 21904 22240 22575 22907 23237 23565 23891 24215 24537 24857 25175 25490 25804 26115 26424 26730 27035 27337 27637 27935 28230 28524 | 0,80 81 82 83 84 85 86 87 88 89 0,90 91 92 93 94 95 96 97 98 99 1.00 01 02 03 04 05 06 07 08 09 1,10 11 12 13 14 15 16 17 18 19 | 0,28814 29103 29389 29673 29955 30234 30511 30785 31057 31327 31594 31859 32121 32381 32639 32894 33147 33398 33646 33891 34134 34375 34614 34850 35083 35314 35543 35769 35993 36214 36433 36650 36864 37076 37286 37493 37698 37900 38100 38298 | 1,20 21 22 23 24 25 26 27 28 29 1,30 31 32 33 34 35 36 37 38 39 1,40 41 42 43 44 45 46 47 48 49 1,50 51 52 53 54 55 56 57 58 59 | 0,38493 38686 38877 39065 39251 39435 39617 39796 39973 40147 40320 40490 40658 40824 40988 41149 41309 41466 41621 41774 41924 42073 42220 42364 42507 42647 42786 42922 43056 43189 43319 43448 43574 43699 43822 43943 44062 44179 44295 44408 | 1,60 61 62 63 64 65 66 67 68 69 1,70 71 72 73 74 75 76 77 78 79 1,80 81 82 83 84 85 86 87 88 89 1,90 91 92 93 94 95 96 97 98 99 | 0,44520 44630 44738 44845 44950 45053 45154 45254 45352 45449 45543 45637 45728 45818 45907 45994 46080 46164 46246 46327 46407 46485 46562 46638 46712 46784 46856 46926 46995 47062 47128 47193 47257 47320 47381 47441 47500 47558 47615 47670 | 2,00 01 02 03 04 05 06 07 08 09 2,10 11 12 13 14 15 16 17 18 19 2,20 21 22 23 24 25 26 27 28 29 2,30 31 32 33 34 35 36 37 38 39 | 47725 47778 47831 47882 47932 47932 48030 48077 48124 48169 48214 48257 48300 48311 48382 48422 48461 48500 48537 48574 48610 48645 48679 48713 48745 48778 48809 48840 48870 48899 48928 48956 48983 49010 49036 49061 49086 49111 49134 49158 |
Продолжение Значение функции Лапласа 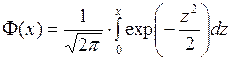
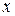
| 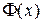
| 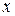
| 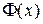
| 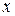
| 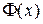
| 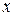
| 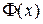
|
| 2,40 41 42 43 44 45 46 47 48 49 2,50 51 52 53 54 55 56 57 58 59 | 0,49180 49202 49224 49245 49266 49286 49305 49124 49343 49361 0,49379 49396 49413 49430 49446 49461 49477 49492 49506 49520 | 2,60 61 62 63 64 65 66 67 68 69 2,70 71 72 73 74 75 76 77 78 79 | 0,49534 49547 49560 49573 49585 49598 49609 49621 49632 49643 0,49653 49664 49674 49683 49693 49702 49711 49720 49728 49736 | 2,80 81 82 83 84 85 86 87 88 89 2,90 91 92 93 94 95 96 97 98 99 | 0,49744 49752 49760 49767 49774 49781 49788 49795 49801 49807 0,49813 49819 49825 49831 49836 49841 49846 49851 49856 49861 | 3,0 1 2 3 4 5 6 7 8 9 4,0 4,5 5,0 | 0,40865 49903 49931 49952 49966 49977 49984 49989 49993 49995 499968 499997 499999 |
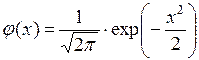
Таблица 2. Значение функции
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 0,0389 | 3989 | 3989 | 3988 | 3986 | 3984 | 3982 | 3980 | 3977 | 3973 |
| 0,1 | 3970 | 3965 | 3961 | 3956 | 3951 | 3945 | 3939 | 3932 | 3925 | 3918 |
| 0,2 | 3910 | 3902 | 3894 | 3885 | 3876 | 3867 | 3857 | 3847 | 3836 | 3825 |
| 0,3 | 3814 | 3802 | 3790 | 3778 | 3765 | 3752 | 3739 | 3726 | 3712 | 3697 |
| 0,4 | 3683 | 3668 | 3653 | 3637 | 3621 | 3605 | 3589 | 3572 | 3555 | 3538 |
| 0,5 | 3521 | 3503 | 3485 | 3467 | 3448 | 3429 | 3410 | 3391 | 3372 | 3352 |
| 0,6 | 3332 | 3312 | 3292 | 3271 | 3251 | 3230 | 3209 | 3187 | 3166 | 3144 |
| 0,7 | 3123 | 3101 | 3079 | 3056 | 3034 | 3011 | 2989 | 2966 | 2943 | 2920 |
| 0,8 | 2897 | 2874 | 2850 | 2827 | 2803 | 2780 | 2756 | 2732 | 2709 | 2685 |
| 0,9 | 2661 | 2637 | 2613 | 2589 | 2565 | 2541 | 2516 | 2492 | 2468 | 2444 |
| 1,0 | 0,2420 | 2396 | 2371 | 2347 | 2323 | 2299 | 2275 | 2251 | 2227 | 2203 |
| 1,1 | 2179 | 2155 | 2131 | 2107 | 2083 | 2059 | 2036 | 2012 | 1989 | 1965 |
| 1,2 | 1942 | 1919 | 1895 | 1872 | 1849 | 1826 | 1804 | 1781 | 1758 | 1736 |
| 1,3 | 1714 | 1691 | 1669 | 1647 | 1626 | 1604 | 1582 | 1561 | 1539 | 1518 |
| 1,4 | 1497 | 1476 | 1456 | 1435 | 1415 | 1394 | 1374 | 1354 | 1334 | 1315 |
| 1,5 | 1295 | 1276 | 1257 | 1238 | 1219 | 1200 | 1182 | 1163 | 1145 | 1127 |
| 1,6 | 1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 1006 | 0989 | 0973 | 0957 |
| 1,7 | 0940 | 0925 | 0909 | 0893 | 0878 | 0863 | 0848 | 0833 | 0818 | 0804 |
| 1,8 | 0790 | 0775 | 0761 | 0748 | 0734 | 0721 | 0707 | 0694 | 0681 | 0669 |
| 1,9 | 0656 | 0644 | 0632 | 0620 | 0608 | 0596 | 0584 | 0573 | 0562 | 0551 |
| 2,0 | 0,0540 | 0529 | 0519 | 0508 | 0498 | 0488 | 0478 | 0468 | 0459 | 0449 |
| 2,1 | 0440 | 0431 | 0422 | 0413 | 0404 | 0396 | 0387 | 0379 | 0371 | 0363 |
| 2,2 | 0355 | 0347 | 0339 | 0332 | 0325 | 0317 | 0310 | 0303 | 0297 | 0290 |
| 2,3 | 0283 | 0277 | 0270 | 0264 | 0258 | 0252 | 0246 | 0241 | 0235 | 0229 |
| 2,4 | 0224 | 0219 | 0213 | 0208 | 0203 | 0198 | 0194 | 0189 | 0184 | 0180 |
| 2,5 | 0175 | 0171 | 0167 | 0163 | 0158 | 0154 | 0151 | 0147 | 0143 | 0139 |
| 2,6 | 0136 | 0132 | 0129 | 0126 | 0122 | 0119 | 0116 | 0113 | 0110 | 0107 |
| 2,7 | 0104 | 0101 | 0099 | 0096 | 0093 | 0091 | 0088 | 0086 | 0084 | 0081 |
| 2,8 | 0079 | 0077 | 0075 | 0073 | 0071 | 0069 | 0067 | 0065 | 0О63 | 0061 |
| 2,9 | 0060 | 0058 | 0056 | 0055 | 0053 | 0051 | 0050 | 0048 | 0047 | 0046 |
| 3,0 | 0,0044 | 0043 | 0042 | 0040 | 0039 | 0038 | 0037 | 0036 | 0035 | 0034 |
| 3,1 | 0033 | 0032 | 0031 | 0030 | 0029 | 0028 | 0027 | 0026 | 0025 | 0025 |
| 3,2 | 0024 | 0023 | 0022 | 0022 | 0021 | 0020 | 0020 | 0019 | 0018 | 0018 |
| 3,3 | 0017 | 0017 | 0016 | 0016 | 0015 | 0015 | 0014 | 0014 | 0013 | 0013 |
| 3,4 | 0012 | 0012 | 0012 | 0011 | 0011 | 0010 | 0010 | 0010 | 0009 | 0009 |
| 3,5 | 0009 | 0008 | 0008 | 0008 | 0008 | 0007 | 0007 | 0007 | 0007 | 0006 |
| 3,6 | 0006 | 0006 | 0006 | 0005 | 0005 | 0005 | 0005 | 0005 | 0005 | 0004 |
| 3,7 | 0004 | 0004 | 0004 | 0004 | 0004 | 0004 | 0003 | 0003 | 0003 | 0003 |
| 3,8 | 0003 | 0003 | 0003 | 0003 | 0003 | 0002 | 0002 | 0002 | 0002 | 0002 |
| 3,9 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0001 | 0001 |
Таблица 3. Критические точки распределения
| Число уровней свободы k | Уровень значимости a | ||||||
| 0,01 | 0,02 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 | |
| 1 | 6,6 | 5,4 | 5,0 | 3,8 | 0,0039 | 0,00098 | 0,00016 |
| 2 | 9,2 | 7,8 | 7,4 | 6,0 | 0,103 | 0,051 | 0,020 |
| 3 | 11,3 | 9,8 | 9,3 | 7,8 | 0,352 | 0,216 | 0,115 |
| 4 | 13,3 | 11,7 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 |
| 5 | 15,1 | 13,4 | 12,8 | 11,1 | 1,15 | 0,831 | 0,554 |
| 6 | 16,8 | 15,0 | 14,4 | 12,6 | 1,64 | 1,24 | 0,872 |
| 7 | 18,5 | 16,6 | 16,0 | 14,1 | 2,17 | 1,69 | 1,24 |
| 8 | 20,1 | 18,2 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 |
| 9 | 21,7 | 19,7 | 19,0 | 16,9 | 3,33 | 2,70 | 2,09 |
| 10 | 23,2 | 21,2 | 20,5 | 18,3 | 3,94 | 3,25 | 2,56 |
| 11 | 24,7 | 22,6 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 |
| 12 | 26,2 | 24,1 | 23,3 | 21,0 | 5,23 | 4,40 | 3,57 |
| 13 | 27,7 | 25,5 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 |
| 14 | 29,1 | 26,9 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 |
| 15 | 30,6 | 28,3 | 27,5 | 25,0 | 7,26 | 6,26 | 5,23 |
| 16 | 32,0 | 29,6 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 |
| 17 | 33,4 | 31,0 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 |
| 18 | 34,8 | 32,3 | 31,5 | 28,9 | 9,39 | 8,23 | 7,01 |
| 19 | 36,2 | 33,7 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 |
| 20 | 37,6 | 35,0 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 |
| 21 | 38,9 | 36,3 | 35,5 | 32,7 | 11,6 | 10,3 | 8,90 |
| 22 | 40,3 | 37,7 | 36,8 | 33,9 | 12,3 | 11,0 | 9,54 |
| 23 | 41,6 | 39,0 | 38,1 | 35,2 | 13,1 | 11,7 | 10,2 |
| 24 | 43,0 | 40,3 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 |
| 25 | 44,3 | 41,6 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 |
| 26 | 45,6 | 42,9 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 |
| 27 | 47,0 | 44,1 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 |
| 28 | 48,3 | 45,4 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 |
| 29 | 49,6 | 46,7 | 45,7 | 42,6 | 17,7 | 16,0 | 14,3 |
| 30 | 50,9 | 48,0 | 47,0 | 43,8 | 18,5 | 16,8 | 15,0 |
Таблица 4. Критические значения критерия знаков G
для уровней статистической значимости
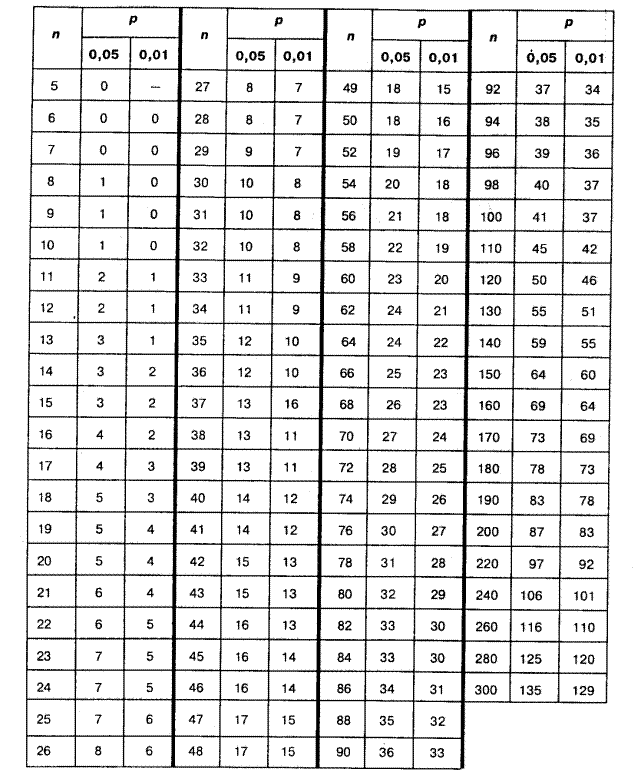
Таблица 5. Критические значения критерия Т-Вилкоксона
для уровней статистической значимости р£0,05 та р£0,01
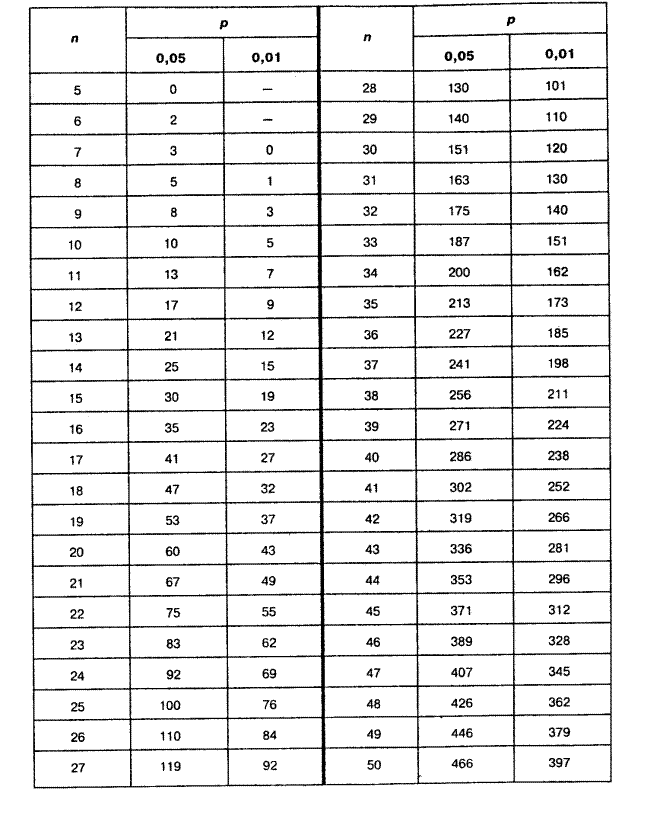
Таблица 6. Критические значения коэффициента Стьюдента (t-критерия)
для разной доверительной вероятности p и числа мер свободы k:
| k | p | |||||||
| 0,80 | 0,90 | 0,95 | 0,98 | 0,99 | 0,995 | 0,998 | 0,999 | |
| 1 | 3,0770 | 6,3130 | 12,7060 | 31,820 | 63,656 | 127,656 | 318,306 | 636,619 |
| 2 | 1,8850 | 2,9200 | 4,3020 | 6,964 | 9,924 | 14,089 | 22,327 | 31,599 |
| 3 | 1,6377 | 2,35340 | 3,182 | 4,540 | 5,840 | 7,458 | 10,214 | 12,924 |
| 4 | 1,5332 | 2,13180 | 2,776 | 3,746 | 4,604 | 5,597 | 7,173 | 8,610 |
| 5 | 1,4759 | 2,01500 | 2,570 | 3,649 | 4,0321 | 4,773 | 5,893 | 6,863 |
| 6 | 1,4390 | 1,943 | 2,4460 | 3,1420 | 3,7070 | 4,316 | 5,2070 | 5,958 |
| 7 | 1,4149 | 1,8946 | 2,3646 | 2,998 | 3,4995 | 4,2293 | 4,785 | 5,4079 |
| 8 | 1,3968 | 1,8596 | 2,3060 | 2,8965 | 3,3554 | 3,832 | 4,5008 | 5,0413 |
| 9 | 1,3830 | 1,8331 | 2,2622 | 2,8214 | 3,2498 | 3,6897 | 4,2968 | 4,780 |
| 10 | 1,3720 | 1,8125 | 2,2281 | 2,7638 | 3,1693 | 3,5814 | 4,1437 | 4,5869 |
| 11 | 1,363 | 1,795 | 2,201 | 2,718 | 3,105 | 3,496 | 4,024 | 4,437 |
| 12 | 1,3562 | 1,7823 | 2,1788 | 2,6810 | 3,0845 | 3,4284 | 3,929 | 4,178 |
| 13 | 1,3502 | 1,7709 | 2,1604 | 2,6503 | 3,1123 | 3,3725 | 3,852 | 4,220 |
| 14 | 1,3450 | 1,7613 | 2,1448 | 2,6245 | 2,976 | 3,3257 | 3,787 | 4,140 |
| 15 | 1,3406 | 1,7530 | 2,1314 | 2,6025 | 2,9467 | 3,2860 | 3,732 | 4,072 |
| 16 | 1,3360 | 1,7450 | 2,1190 | 2,5830 | 2,9200 | 3,2520 | 3,6860 | 4,0150 |
| 17 | 1,3334 | 1,7396 | 2,1098 | 2,5668 | 2,8982 | 3,2224 | 3,6458 | 3,965 |
| 18 | 1,3304 | 1,7341 | 2,1009 | 2,5514 | 2,8784 | 3,1966 | 3,6105 | 3,9216 |
| 19 | 1,3277 | 1,7291 | 2,0930 | 2,5395 | 2,8609 | 3,1737 | 3,5794 | 3,8834 |
| 20 | 1,3253 | 1,7247 | 2,08600 | 2,5280 | 2,8453 | 3,1534 | 3,5518 | 3,8495 |
| 21 | 1,3230 | 1,7200 | 2,2,0790 | 2,5170 | 2,8310 | 3,1350 | 3,5270 | 3,8190 |
| 22 | 1,3212 | 1,7117 | 2,0739 | 2,5083 | 2,8188 | 3,1188 | 3,5050 | 3,7921 |
| 23 | 1,3195 | 1,7139 | 2,0687 | 2,4999 | 2,8073 | 3,1040 | 3,4850 | 3,7676 |
| 24 | 1,3178 | 1,7109 | 2,0639 | 2,4922 | 2,7969 | 3,0905 | 3,4668 | 3,7454 |
| 25 | 1,3163 | 1,7081 | 2,0595 | 2,4851 | 2,7874 | 3,0782 | 3,4502 | 3,7251 |
| 26 | 1,315 | 1,705 | 2,059 | 2,478 | 2,778 | 3,0660 | 3,4360 | 3,7060 |
| 27 | 1,3137 | 1,7033 | 2,0518 | 2,4727 | 2,7707 | 3,0565 | 3,4210 | 3,6896 |
| 28 | 1,3125 | 1,7011 | 2,0484 | 2,4671 | 2,7633 | 3,0469 | 3,4082 | 3,6739 |
| 29 | 1,3114 | 1,6991 | 2,0452 | 2,4620 | 2,7564 | 3,0360 | 3,3962 | 3,8494 |
| 30 | 1,3104 | 1,6973 | 2,0423 | 2,4573 | 2,7500 | 3,0298 | 3,3852 | 3,6460 |
| 32 | 1,3080 | 1,6930 | 2,0360 | 2,4480 | 2,7380 | 3,0140 | 3,3650 | 3,6210 |
| 34 | 1,3070 | 1,6909 | 2,0322 | 2,4411 | 2,7284 | 3,9520 | 3,3479 | 3,6007 |
| 36 | 1,3050 | 1,6883 | 2,0281 | 2,4345 | 2,7195 | 9,490 | 3,3326 | 3,5821 |
Продолжение Таблицы 6. Критические значения коэффициента Стьюдента (t-критерия) для разной доверительной вероятности p и числа мер свободы k:
| k | p | |||||||
| 0,80 | 0,90 | 0,95 | 0,98 | 0,99 | 0,995 | 0,998 | 0,999 | |
| 38 | 1,3042 | 1,6860 | 2,0244 | 2,4286 | 2,7116 | 3,9808 | 3,3190 | 3,5657 |
| 40 | 1,303 | 1,6839 | 2,0211 | 2,4233 | 2,7045 | 3,9712 | 3,3069 | 3,5510 |
| 42 | 1,320 | 1,682 | 2,018 | 2,418 | 2,6980 | 2,6930 | 3,2960 | 3,5370 |
| 44 | 1,301 | 1,6802 | 2,0154 | 2,4141 | 2,6923 | 3,9555 | 3,2861 | 3,5258 |
| 46 | 1,300 | 1,6767 | 2,0129 | 2,4102 | 2,6870 | 3,9488 | 3,2771 | 3,5150 |
| 48 | 1,299 | 1,6772 | 2,0106 | 2,4056 | 2,6822 | 3,9426 | 3,2689 | 3,5051 |
| 50 | 1,298 | 1,6759 | 2,0086 | 2,4033 | 2,6778 | 3,9370 | 3,2614 | 3,4060 |
| 55 | 1,2997 | 1,673 | 2,0040 | 2,3960 | 2,6680 | 2,9240 | 3,2560 | 3,4760 |
| 60 | 1,2958 | 1,6706 | 2,0003 | 2,3901 | 2,6603 | 3,9146 | 3,2317 | 3,4602 |
| 65 | 1,2947 | 1,6686 | 1,997 | 2,3851 | 2,6536 | 3,9060 | 3,2204 | 3,4466 |
| 70 | 1,2938 | 1,6689 | 1,9944 | 2,3808 | 2,6479 | 3,8987 | 3,2108 | 3,4350 |
| 80 | 1,2820 | 1,6640 | 1,9900 | 2,3730 | 2,6380 | 2,8870 | 3,1950 | 3,4160 |
| 90 | 1,2910 | 1,6620 | 1,9867 | 2,3885 | 2,6316 | 2,8779 | 3,1833 | 3,4019 |
| 100 | 1,2901 | 1,6602 | 1,9840 | 2,3642 | 2,6259 | 2,8707 | 3,1737 | 3,3905 |
| 120 | 1,2888 | 1,6577 | 1,9719 | 2,3578 | 2,6174 | 2,8598 | 3,1595 | 3,3735 |
| 150 | 1,2872 | 1,6551 | 1,9759 | 2,3515 | 2,6090 | 2,8482 | 3,1455 | 3,3566 |
| 200 | 1,2858 | 1,6525 | 1,9719 | 2,3451 | 2,6006 | 2,8385 | 3,1315 | 3,3398 |
| 250 | 1,2849 | 1,6510 | 1,9695 | 2,3414 | 2,5966 | 2,8222 | 3,1232 | 3,3299 |
| 300 | 1,2844 | 1,6499 | 1,9679 | 2,3388 | 2,5923 | 2,8279 | 3,1176 | 3,3233 |
| 400 | 1,2837 | 1,6487 | 1,9659 | 2,3357 | 2,5882 | 2,8227 | 3,1107 | 3,3150 |
| 500 | 1,2830 | 1,6470 | 1,9640 | 2,3330 | 2,7850 | 2,8190 | 3,1060 | 3,3100 |
Таблица 7. Критические значения критерия U-Вилкоксона-Манна-Уитни для  уровней статистической значимости р£0,05 и р£0,01
уровней статистической значимости р£0,05 и р£0,01
Дата: 2018-12-21, просмотров: 381.
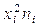
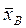
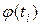
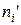
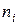
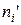
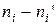
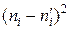
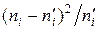
 6
6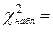 7,1
7,1