МАТЕМАТИКА
Методические указания, рабочая программа и контрольные задания для студентов-заочников I и II курсов на базе
9 классов Челябинского монтажного колледжа
Челябинск 2010

Составитель: Смирнова Л.Л. преподаватель математики Челябинского монтажного колледжа
Пояснительная записка
Данное пособие ставит своей целью оказание помощи студенту-заочнику в организации его самостоятельной работы по овладению системой знаний, умений и навыков в объеме действующей программы.
Прежде чем приступить к выполнению контрольных заданий, необходимо повторить курс математики неполной средней школы, уделить особое внимание правилам действий над дробями, пропорциями, процентами, преобразованиям алгебраических выражений, повторить сведения о функциях и числовых последовательностях в объеме школьной программы. Необходимо познакомиться с принятой математической символикой. Для повторения рекомендуются учебники для школ и техникумов.
В соответствии с учебным планом студенты-заочники по курсу «Математика» выполняют четыре контрольные работы, сдают один зачет (1-й курс, летняя сессия) и один экзамен (2-й курс, летняя сессия).
Каждое контрольное задание имеет 10 вариантов. Вариант контрольной работы выбирается по последней цифре личного дела (шифра) студента-заочника. Номера задач для контрольных работ указаны в таблице.
При выполнении контрольной работы надо соблюдать следующие правила:
1. Каждая работа выполняется в отдельной тетради, на обложке которой указывается название предмета, номер работы, номер варианта, фамилия, имя, отчество и шифр студента-заочника.
2. Контрольная работа должна быть написана чернилами, аккуратно и разборчиво. Для замечаний должны быть оставлены поля 3 - 4 см. Чертежи выполняются с помощью чертежных инструментов. Замечания рецензента исправлять и стирать нельзя.
3. Условие задачи необходимо записывать полностью. К геометрическим задачам нужно также делать краткую запись условия.
4. Решения задач должны сопровождаться краткими, но достаточными объяснениями. Для решения задачи использовать необходимые вычислительные средства (М.К., справочник и т.д.).
5. Проверенные работы сохраняются и представляются на экзамене.
6. Если работа не зачтена, то ее нужно переделать заново и сдать на повторную рецензию.
7. Несмотря на то, что в пособии даются разъяснения и указания, основной материал следует изучать по учебникам.
| Номер варианта | К. р. № 1 | K.р. | № 2 | К. р. № 3 | К. р. № 4 | |
| 1 | 1, | 11, 21 | 1, 11, | 21, 31 | 1, 11, 21 | 1, 11, 21, 31 |
| 2 | 2, | 12, 22 | 2, 12, | 22, 32 | 2, 12, 22 | 2, 12, 22, 32 |
| 3 | 3, | 13, 23 | 3, 13, | 23, 33 | 3, 13, 23 | 3, 13, 23, 33 |
| 4 | 4, | 14, 24 | 4, 14, | 24, 34 | 4, 14, 24 | 4, 14, 24, 34 |
| 5 | 5, | 15, 25 | 5, 15, | 25, 35 | 5, 15, 25 | 5, 15, 25, 35 |
| 6 | 6, | 16, 26 | 6, 16, | 26, 36 | 6, 16, 26 | 6, 16, 26, 36 |
| 7 | 7, | 17, 27 | 7, 17, | 27, 37 | 7, 17, 27 | 7, 17, 27, 37 |
| 8 | 8, | 18, 28 | 8, 18, | 28, 38 | 8, 18, 28 | 8, 18, 28, 38 |
| 9 | 9, | 19, 29 | 9, 19, | 29, 39 | 9, 19, 29 | 9, 19, 29, 39 |
| 0 | 10 | 10, 20, 30 | 10, 20, 30, 40 | 10, 20, 30 | 10, 20, 30, 40 | |
Литература
1. Зайцев И.Л. Элементы высшей математики - М.: Наука, 1994.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Т. 1,2, - М.: Наука, 1993.
3. Андреев П.П. и др. Геометрия. - М.: Наука, 1998.
4. Данко П.Е. и др. Высшая математика в упражнениях и задачах. -М.: Высшая школа, 2005. - .
5. Клопский В.М. и др. Геометрия. - М.: Просвещение, 1999.
Тематический план курса «Математика»
| № |
Темы
Разделы и темы
Максимальная нагрузка
студента
Количество аудиторных часов при заочной форме обучения
Самостоя-тельная работа студента
Всего
В том числе
|
№ Темы |
Разделы и темы |
Макси- Мальная нагрузка студента |
Всего |
В том числе | |||
| Лабора-торные работы | Практи- ческие занятия | ||||||
| Раздел 6: Прямые и плоскости в пространстве. | 16 | - | - | - | 16 | ||
| 6.1 | Начальные понятия стереометрии и взаимное расположение прямых и плоскостей в пространстве. | 10 | - | - | - | 10 | |
| 6.2 | Двугранные углы. | 6 | - | - | - | 6 | |
| Итого: | 16 | - | - | - | 16 | ||
| Раздел 7: Геометрические тела и поверхности. | 12 | - | - | - | 12 | ||
| 7.1 | Многогранники. | 6 | - | - | - | 6 | |
| 7.2 | Тела вращения. | 6 | - | - | - | 6 | |
| Итого: | 12 | - | - | - | 12 | ||
| Раздел 8: Объемы и площади поверхностей геометрических тел. | 18 | - | - | - | 18 | ||
| 8.1 | Объемы геометрических тел. | 10 | - | - | - | 10 | |
| 8.2 | Площади поверхностей. | 8 | - | - | - | 8 | |
| Итого: | 18 | - | - | - | 18 | ||
| Раздел 9: Дифференциальное исчисление. | 25 | 14 | - | 14 | 11 | ||
| 9.1 | Производная функции. | 14 | 10 | - | 10 | 4 | |
| 9.2 | Исследование функции с помощью производной. | 11 | 4 | - | 4 | 7 | |
| Итого: | 25 | 14 | - | 14 | 11 | ||
| Раздел 10: Интегральное исчисление. | 26 | 12 | - | 12 | 14 | ||
| 10.1 | Неопределенный интеграл. | 10 | 6 | - | 6 | 4 | |
| 10.2 | Определенный интеграл. | 16 | 6 | - | 6 | 10 | |
| Итого: | 26 | 12 | - | 12 | 14 | ||
| Всего: | 202 | 54 | - | 54 | 148 | ||
III . Векторная алгебра .
3.1. Разложение вектора по векторам базиса. Линейные операции над векторами в координатной форме. Определение длины и направления векторов.
3.2. Скалярное произведение двух векторов. Координатная форма скалярного произведения. Угол между векторами. Условие параллельности и перпендикулярности векторов. Определение проекции одного вектора на другой.
3.3. Векторное произведение двух векторов. Векторное произведение в координатной форме. Площадь треугольника и параллелограмма. Понятие о смешанном скалярном векторном произведении. Объем параллелепипеда.
Переменной .
8.1. Первообразная и ее свойства. Неопределенный интеграл и его свойства. Таблица основных интегралов.
8.2. Основные методы интегрирования, непосредственное интегрирование, метод подстановки, интегрирование по частям.
8.3. Определенный интеграл и его свойства. Основные методы интегрирования. Вычисление площадей криволинейных трапеций.
Геометрических тел .
10.1. Площади поверхностей призмы, параллелепипеда, пирамиды, усеченной пирамиды.
10.2 Площади поверхностей цилиндра, конуса, шара и его частей.
10.3 Объем призмы, параллелепипеда, пирамиды, усеченной пирамиды.
10. 4. Объемы тел вращения: цилиндр, конус, шар.
ЗАДАНИЯ НА КОНТРОЛЬНЫЕ РАБОТЫ
Тема I. Элементы линейной алгебры
Знакомство с использованием определителей начните с простейшего случая решения и исследования системы двух линейных уравнений с двумя неизвестными. Изучите свойства определителя второго, а затем третьего порядка.
Особое внимание обратите на то, что вычисление определителей упрощается, если умело пользоваться свойствами определителей.
При изучении вопросов, связанных с исследованием систем линейных уравнений, не упустите из виду случай, когда главный определитель системы равен нулю. В этой ситуации формулы Крамера теряют смысл и соответствующие системы уравнений либо несовместны, либо имеют бесчисленное множество решений.
Пример : Используя формулы Крамера, решить систему и сделать проверку.
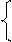 x – 2y + z = 4,
x – 2y + z = 4,
2x + y + 3z = 5
3x + 4y + z = –2.
Подсчитаем главный определитель системы D, используя правило вычисления определителей третьего порядка:







 a11 a12 a13
a11 a12 a13
D = b21 b22 b23 =a11 * b22 b23 – a12 * b21b23 + a13 b21b22
c31 c32 c33 c32 c33 c31 c33 c31c32
Имеем:

 1 –2 1
1 –2 1
D = 2 1 3 = 1* (1–12) + 2 * (2 – 9) +1 * (8 – 3) = – 20.
3 4 1
Так как D ≠ 0, то система имеет единственное решение. Для его отыскания вычислим вспомогательные определители: Dх, Dу, Dz.

 4 –2 1
4 –2 1
Dx = 5 1 3 = 4 * (1 -12) – (–2) * (5+6) +1 * (20+2) = 0;
–2 4 1

 1 4 1
1 4 1
Dy= 2 5 3 = 1*(5 + б) – 4*(2 – 9) + 1*(– 4 – 15) = 20;
3 -2 1

 1 -2 4
1 -2 4
Dz = 2 1 5 = 1*(−2 – 20) – (– 2) *(–4 –15) + 4*(8 – 3) = – 40.
3 4 –2
Найдем неизвестные по формуле Крамера:
x = 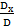 = 0; y =
= 0; y = 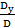 = – 1; z =
= – 1; z = 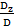 = 2.
= 2.
Проверка осуществляется путем подставления полученного решения в каждое уравнение системы:
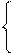 0 – 2 *(–1) + 2 = 4
0 – 2 *(–1) + 2 = 4
2*0 + (–1) + 3*2 = 5
3*0 + 4*(–1) +2 = -2
Все три равенства верные, следовательно, ответ имеет вид (0; –1; 2).
Тема II. Элементы аналитической геометрии
При изучении этой темы, прежде всего, следует усвоить понятие уравнения линии. Подобно тому, как точка в аналитической геометрии определяется координатами, линия определяется уравнением, связывающим координаты любой точки этой линии. Прямая линия является простейшей из линий на плоскости. Изучите различные способы нахождения уравнения прямой, а также плоскости.
Успех решения задач во многом зависит от умелого выбора соответствующего вида уравнения прямой и плоскости.
Пример: Даны координаты вершин треугольника ABC A(-1;2), В(5;-1), С(-4;-5).
 1) Расстояние l между точками M1 (х1;у1) и М2 ('х2;у2) находим по формуле: l = |М4 М2| =
1) Расстояние l между точками M1 (х1;у1) и М2 ('х2;у2) находим по формуле: l = |М4 М2| = 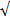 ( x2 – х1)2 + ( у2 – у1)2.
( x2 – х1)2 + ( у2 – у1)2.
По этой формуле находим длину стороны АВ:
AB| = 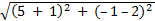 =
= 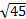 = 3
= 3 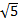 .
.
2) Уравнение прямой, проходящей через две точки плоскости M1 (x1; y1) и М2 (х2; у2) имеет вид
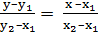 (1)
(1)
Подставляя в это уравнение координаты точек А и В, получаем уравнение стороны АВ:
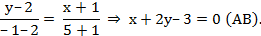
Угловой коэффициент k А B прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом у = kx + b.
У нас 2у = -х+3 => y= – 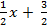 .
.
Следовательно, kAB = –  .
.
Аналогично находим kBC =  .
.
3) Для нахождения внутреннего угла треугольника ABC воспользуемся формулой
tgB = 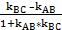 .
.
Отметим, что порядок разности угловых коэффициентов, стоящей в числителе дроби, зависит от взаимного расположения прямых АВ и ВС. Подумайте, как бы вы стали искать внутренние углы А и С треугольника ABC?
Подставим значения kАВ и kвс в формулу. Находим
tgB = 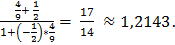
По таблицам В.М. Брадиса или на инженерном микрокалькуляторе получаем 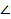 B
B 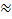 50°.
50°.
|
XM = 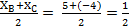
yM = 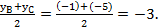
Теперь подставим в (1) координаты точек А и М, получаем уравнение медианы:
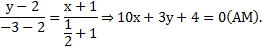
5) Для составления уравнения высоты CD, воспользуемся уравнением прямой, проходящей через точку M0 (x0; y0) с заданным угловым коэффициентом k, которое имеет вид
y − yo= k*(x - xo) (2)
и условием перпендикулярности АВ и CD, которое выражается соотношением
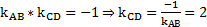 .
.
Подставим в (2) 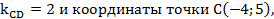 получим уравнение высоты СD:
получим уравнение высоты СD:
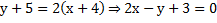 (CD).
(CD).
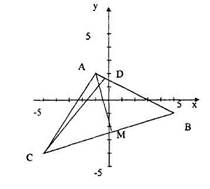 |
6)
Тема III. Векторная алгебра
В основе этой темы лежит понятие вектора и его координат на плоскости и в пространстве. Узловыми моментами являются действия с векторами: сложение и вычитание векторов, умножение вектора на число, скалярное и векторное произведение двух векторов, смешанное произведение трех векторов. Особое внимание следует обратить на область применения каждого вида произведений векторов при решении задач геометрии (вычислении углов, площадей, объемов)
После подробного изучения элементов векторной алгебры следует перейти к вопросам, связанным с составлением уравнений плоскости и прямой в пространстве.
Пример: Даны координаты вершин пирамиды А(0;0;1), В(2; 3;5), С(6;2;3), D(3;7;2).
1) Известно, что произвольный вектор 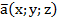 раскладывается по векторам базиса
раскладывается по векторам базиса 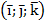 по формуле:
по формуле:
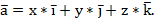
Если заданы точки M1 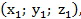 M2
M2 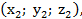
то 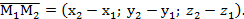
Значит, 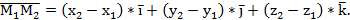
Подставим
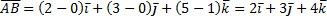
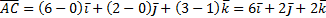
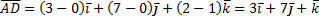
Если 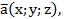 то
то 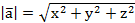
Подставим
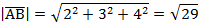
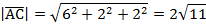
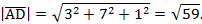
2) Известна формула
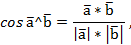
где 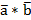 – скалярное произведение векторов
– скалярное произведение векторов 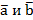 , которое вычисляется по формуле
, которое вычисляется по формуле
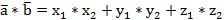 ,
,
где 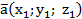 ,
, 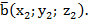
Подставим
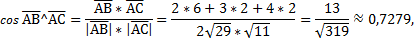
то есть 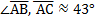 .
.

 3) Известно, что
3) Известно, что 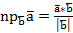 .
.
Следовательно, у нас 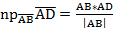 .
.


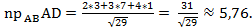
4) По формуле нахождения площади треугольника, построенного на векторах 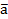 и
и 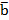 ,
,
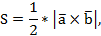
где 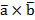 – векторное произведение векторов, которое вычисляется следующим образом:
– векторное произведение векторов, которое вычисляется следующим образом:
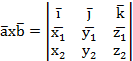 .
.
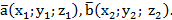
У нас 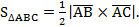
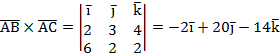 .
.
Следовательно, 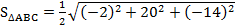 = 5
= 5 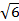
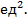
5) Объем пирамиды, построенной на трех векторах
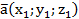 ,
,
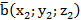 ,
,
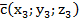 .
.
находится по формуле 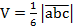 , где
, где 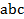 – смешанное произведение векторов, которое вычисляется следующим образом:
– смешанное произведение векторов, которое вычисляется следующим образом:
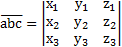 .
.
У нас 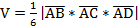 ,
,
где
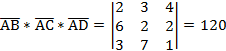 ,
,
то есть 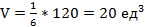 .
.
6) Известно, что уравнение прямой, проходящей через две точки
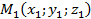
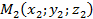
имеет вид: 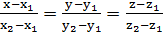 .
.
Подставим координаты точек A и C, получим
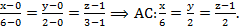
7) Известно, что уравнение плоскости, проходящей через три точки
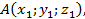
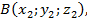
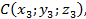
имеет вид 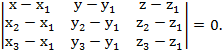
Подставим координаты точек A, B, C, получим
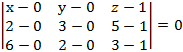
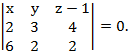
пл.(ABC): x −10y+7z −7 = 0.
Контрольная работа № 1
I. Решить заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.
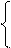
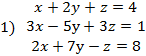
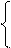
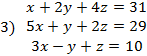
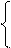
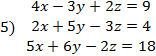
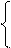
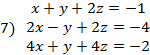
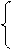
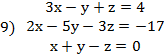
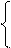
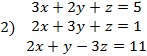
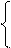
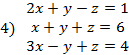
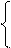
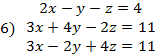
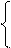
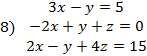
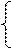
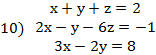
II. Даны координаты вершин треугольника АВС. Найти:
1) длину стороны АВ;
2) уравнение сторон АВ и ВС и их угловые коэффициенты;
3) внутренний угол В;
4) уравнение медианы АЕ;
5) уравнение высоты CD;
6) построить 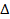 АВС.
АВС.
11) А(1;-1) В(4;3) С(5;1) 12) А(0;1) В(3;5) С(4;3)
13) А(0;-1) В(3;3) С(4;1)
15) А(1;-2) В(4;2) С(5;0)
17) А(2;-2) В(5;2) С(6;0)
19) А(0;0) В(3;4) С(4;2)
14) А (3;-2) В(6;2) С(7;0)
16) А(3;-3) В(6;1) С(7;-1)
18) А(-1;1) В(2;5) С(3;3)
20) А(4;0) В(7;4) С(8;2)
III. Даны координаты вершин пирамиды ABCD. Требуется:
1) разложить векторы 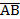 ,
, 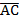 ,
, 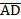 по векторам базиса и найти их модули;
по векторам базиса и найти их модули;
2) найти угол между векторами 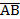 ,
, 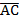 ;
;
3) найти проекцию вектора 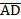 на вектор
на вектор 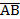 ;
;
4) найти площадь грани ABC;
5) найти объем пирамиды ABCD;
6) составить уравнение ребра АС;
7) составить уравнение грани ABC.
21) А(1;2;1), В(-1;5;1), С(-1;2;7), D(1;5;9)
22) А(2;3;2), В(0;6;2), С(0;3;8), D(2;6;10)
23) А(0;3;2), В(-2;6;2), С(-2;3;8), D(0;6;10)
24) А(2;1;2), В(0;4;2), С(0;1;8), D(2;4;10)
25) А(2;3;0), В(0;6;0), С(0;3;6), D(2;6;8)
26) А(2;2;1), В(0;5;1), С(0;2;7), D(2;5;9)
27) А(1;3;1), В(-1;6;1), С(-1;3;7), D(1;6;9)
28) А(1;2;2), В(-1;5;2), С(-1;2;8), D(1;5;10)
29) А(2;3;1), В(0;6;1), С(0;3;7), D(2;6;9)
30) А(2;2;2), В(0;5;2), С(0;2;8), D(2;5;10)
Вопросы для самоконтроля
1. Перечислите свойства определителей.
2. Какие способы вычисления определителей вы знаете?
3. Какой вид имеют формулы Крамера? В каком случае их можно применять?
4. Сформулируйте условие, при котором система линейных уравнений имеет единственное решение.
5. При каком условии система линейных однородных уравнений имеет ненулевое решение?
6. Как определяются декартовые координаты точки на плоскости?
7. Как вычислить расстояние между двумя точками?
8. Напишите формулы для координат середины отрезка через координаты его концов.
9. Дайте определение линии на плоскости.
10. Как найти координаты точек пересечения двух линий на плоскости, заданных своими уравнениями?
11. Чем отличается уравнение прямой в декартовых координатах от уравнений других линий?
12. Напишите формулу для вычисления угла между двумя прямыми.
13. Как выглядит условие параллельности и перпендикулярности двух прямых?
14. Напишите уравнение прямой, проходящей: а) через заданную точку в заданном направлении; б) через две заданные точки.
15. Как написать уравнение медианы, высоты в прямоугольнике, если известны координаты его вершин?
16. Как определяется сумма и разность двух векторов?
17. Дайте определение коллинеарных и компланарных векторов.
18. Дайте определение проекции вектора на ось.
19. Как выглядит разложение вектора по векторам базиса? Что такое координаты вектора?
20. Как найти угол между векторами?
Как найти длину вектора по его координатам?
21. Каково условие перпендикулярности двух векторов?
22. Как найти вектор перпендикулярный двум данным векторам?
23. Как найти площадь треугольника, построенного на двух векторах?
24. Как найти объем пирамиды с вершинами в заданных точках?
25. Как выглядит уравнение плоскости: а) через заданную точку с заданным нормальным вектором; б) через три заданные точки?
26. Какие вы знаете виды уравнений прямой в пространстве?
27. Как найти расстояние от данной точки до данной плоскости?
Тема IV . Введение в математический анализ
При изучении этой темы следует обратить внимание на понятие функции и изучить ее свойства. Познакомиться со всеми элементарными функциями (линейными, степенными, показательными, логарифмическими, тригонометрическими).
Особое внимание уделить пределу функции в точке и на бесконечность и понятию непрерывной функции.
После подробного изучения свойств пределов, I и II замечательных пределов, следует приступить к непосредственному вычислению пределов элементарных функций и их композиций, учитывая, что под знаком предела можно производить тождественные преобразования выражения.
Примеры :
1) 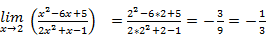
2) 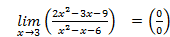
т.к.
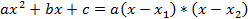
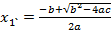 ,
, 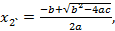
то
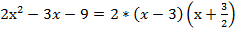
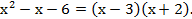
Следовательно, 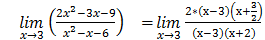 =
=
= 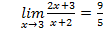 .
.
3) 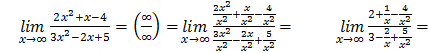 =
= 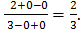
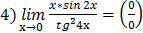 т.к.
т.к. 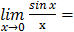 и
и 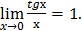
Следовательно, 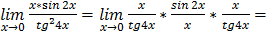
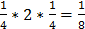 .
.
Тема V . Дифференциальное исчисление
функций одной переменной
В основе этой темы лежит понятие производной. Особое внимание следует обратить на геометрическое и механическое истолкование производной. Особую роль при решении задач играет правило вычисления производной сложной функции.
При дифференцировании некоторых функций нередко значительно упрощает вычисление прием, состоящий в том, что перед вычислением производной функцию предварительно логарифмируют
При решении всех последующих примеров кроме таблицы производных используются правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции:
a) 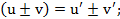
б) 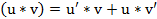 ;
;
в) 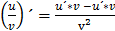 ;
;
г) 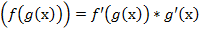
1) y = 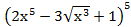
y´= 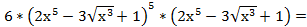
= 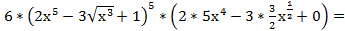
= 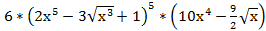 .
.
2) 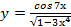
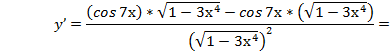
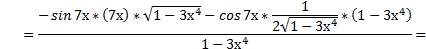
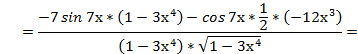
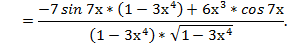
3) 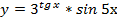
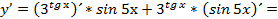
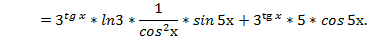
4) 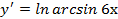
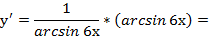
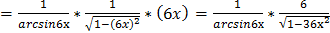 .
.
5) Пусть S(t) =3 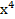 − 2
− 2 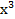 + х – 1
+ х – 1 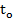 = 2.
= 2.
По формулам имеем
V (t) = S  (t)
(t)
a(t) = S´(t)
У нас
S´(t) = 3∗4∗ 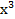 −2∗3 ∗ х2 +1 −0 =12
−2∗3 ∗ х2 +1 −0 =12 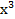 −6
−6 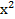 +1.
+1.
S´( 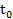 ) = S´(2) =12∗23 − 6∗22 +1 =73
) = S´(2) =12∗23 − 6∗22 +1 =73
V =73 ед.
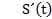 = 12 * 3 *
= 12 * 3 * 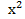 – 6 * 2 *
– 6 * 2 * 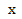 + 0 = 36
+ 0 = 36 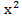 − 12
− 12 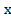
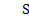 ´
´ 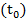 =
= 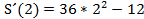 * 2 = 120
* 2 = 120
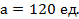
Тема VII Исследование функций одной
переменной
Изучение этой темы следует начать с усвоения понятий возрастания и убывания функции, максимума и минимума функции, выпуклости и вогнутости кривой.
Обратите внимание на следующие обстоятельства:
1. функция, определенная на отрезке, может достигать максимума и минимума только при значениях X, заключенных внутри рассматриваемого отрезка;
2. не следует считать, что максимум и минимум функции являются, соответственно, её наибольшим и наименьшим значениями на рассматриваемом отрезке (например, в точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума).
Целесообразно намечать элементы графика параллельно с исследованием функции.
Пример:
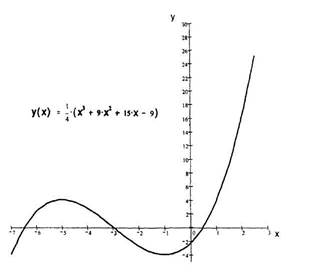
1) Исследуем функцию у =  (х3 + 9х2 +15х - 9).
(х3 + 9х2 +15х - 9).
1. D (x) = (-∞;+∞), т.е. функция непрерывна на всей числовой прямой.
2. Для исследования функции на экстремумы и монотонность необходимо найти производную и приравнять ее к нулю.
Имеем y´ = 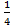 (3x2+9*2x + 15 − 0)
(3x2+9*2x + 15 − 0)
у' = 0 => 3х2+18х + 15= 0
х2+6х + 5 = 0
х1 = -5; х2 = -1
| х | (-∞,-5) | -5 | (-5;-1) | -1 | (-1;+∞) |
| f´(х) | + | 0 | − | 0 | + |
| f (x) | ↗

| max | ↘ | min | ↗ |
уmax (-5)=  ((-5)3+9*(-5)2 +15*(-5) − 9) =4
((-5)3+9*(-5)2 +15*(-5) − 9) =4
уmin (-1) = 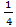 ((-1)3 +9*(-1)2+15*(−1)−9) =−4
((-1)3 +9*(-1)2+15*(−1)−9) =−4
3. Для определения точек перегиба и интервалов вогнутости и выпуклости найдем вторую производную и приравняем ее к нулю
Имеем y´´ = 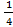 (3 * 2 *x + 18+0)
(3 * 2 *x + 18+0)
6х + 18 = 0
х + 3 = 0
х = -3
| х | (-∞; -3) | -3 | (-3;+∞) |
| f ´(х) | - | 0 | + |
| f (x) | ∩ | т. п | ∪ |
у(-3) =  ((-3)3 + 9(-3)2 + 15(−3) − 9) = 0.
((-3)3 + 9(-3)2 + 15(−3) − 9) = 0.
Точка (-3,0) - точка перегиба.
Контрольная работа №2
I. Вычислить пределы:
1) а) 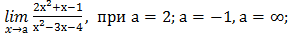
б) 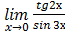 .
.
2) 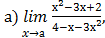 при а= -1; а = 1,а = ∞;
при а= -1; а = 1,а = ∞;
б) 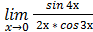 .
.
3) а) 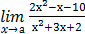 , при а = 2; а = -2; а = ∞;
, при а = 2; а = -2; а = ∞;
б) 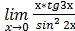 .
.
4) а) 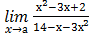 , при а = 1; а = 2; а = ∞;
, при а = 1; а = 2; а = ∞;
б) 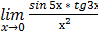 .
.
5) а) 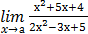 , при а= -2; а = -1; а = ∞;
, при а= -2; а = -1; а = ∞;
б) 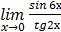 .
.
6) 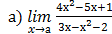 , при а = -1; а = 1; а = ∞;
, при а = -1; а = 1; а = ∞;
б) 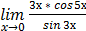
7) а) 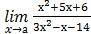 , при а = 2; а = -2; а = ∞;
, при а = 2; а = -2; а = ∞;
б) 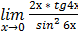 .
.

8) а) 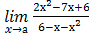 , при а = 1; а = 2; а = ∞;
, при а = 1; а = 2; а = ∞;
б) 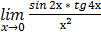 .
.
9) а) 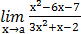 , при а= -2; а= -1; а = ∞;
, при а= -2; а= -1; а = ∞;
б) 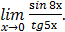
10) а) 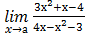 , при а= -1; а = 1; а = ∞;
, при а= -1; а = 1; а = ∞;
б) 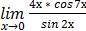 .
.
II. Найти производные функций, пользуясь правилами и формулами дифференцирования:
11) а) у = (3х − 4 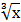 +2)4 б) у =
+2)4 б) у = 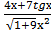
в) у = 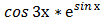 г) у =
г) у = 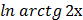
12) а) у = (3 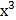 −2
−2 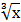 2 −1)2 б) у =
2 −1)2 б) у = 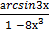
в) у = 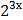 * tg2х г) у = со s
* tg2х г) у = со s 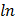 5х
5х
13) а) у = (х2 − 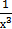 +5
+5 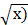 4 б) у =
4 б) у = 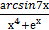
в) у = 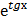 *
* 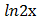 г) у = со s
г) у = со s 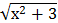
14) а) у = (4 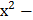 −
− 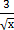 +4)3 б) у =
+4)3 б) у = 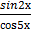
в) у = 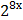 * tg3х г) у =
* tg3х г) у = 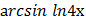
15) а) у = ( 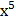 −
− 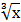 +1)5 б) у =
+1)5 б) у = 
в) у = 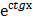 *sin4х г) у = sin
*sin4х г) у = sin 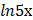
16) а) у = (6 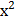 −
− 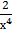 + 5)2 б) у =
+ 5)2 б) у = 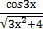
в) у = 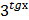 * а rcsinх2 г) у =
* а rcsinх2 г) у = 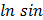 6х
6х
17) а) у = ( 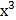 − 4
− 4 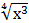 + 2)3 б) у =
+ 2)3 б) у = 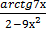
в) у = 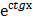 *cos6х г) у =
*cos6х г) у = 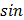
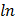 2х
2х
18) а) у = 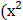 − 2
− 2 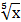 + 4)4 б) у =
+ 4)4 б) у = 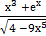
в) у = 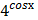 *
* 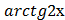 г) у =
г) у = 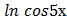
19) а) у = (3 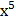 −
− 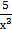 −2)5 б) у =
−2)5 б) у = 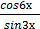
в) у = 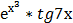 г) у = а rcsin
г) у = а rcsin 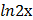
20) а) у = 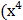 − 2
− 2 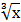 + 1)2 б) у =
+ 1)2 б) у = 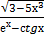
в) у = 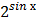 * а rcsin 2х г) у =
* а rcsin 2х г) у = 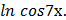
III. Дан закон S(t) изменения пути движения материальной точки. Требуется найти значения скорости и ускорения этой точки в момент времени t0.
21) S (t) = 2x4 −3x2 + x − 2, to= 2
22) S (t) = 3x4 − 2x2 − x + 1, to = 1
23) S(t) = 4x4 − 3x2 −2x −1, to = 2
24) S(t) = x4+x2 −3x + 1, to = 1
25) S(t) = 2x4 −2x2 + x −2, to = 2
26) S(t) = 3x4 − x2 + 2x+1, to= 1
27) S(t) = 4x4 −3x2 − x + 2, to = 2
28) S(t) = 2x4 + 4x2 −5x − 1, to = 1
29) S(t) = 3x4 + x2 − 2x + 1, to = 2
30) S(t) = 4x4 + 2x2 −7x −3, to= 1.
IV. Исследовать данные функции с помощью производной и начертить и графики. Исследования проводить по схеме:
1) найти область определения функции;
2) найти точки экстремума функции и определить интервалы ее монотонности;
3) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика;
4) построить график, используя результаты предыдущих исследований.
31) у = 2х3 − 9х2 + 12х − 5 32) у = х3 − 6х2 + 9х + 1
33) у = х3 − 3х2 − 9х + 10 34) у = х3 + 3х2 − 9х − 10
35) у = х3 + 6х2 + 9х + 2 36) у = 2х3 − 3х2 −12х + 5
37) у = 2х3 + 3х2 −12х − 8 38) у = 2х3 + 9х2 + 12х + 7
39) у = 2х3 − 15х2 + 36х − 32 40) у = 2х3 −3х2 − 36х + 20
Вопросы для самоконтроля
1. Что такое переменная величина?
2. Сформулируйте определение функции. Что называется областью определения функции?
3. Какие способы задания функции вы знаете?
4. Какие функции называются элементарными?
5. Сформулируйте понятие предела переменной величины.
6. Дайте определение предела функции.
7. Какая функция называется ограниченной?
8. В каком случае функция называется бесконечно малой?
9. Сформулируйте основные теоремы о пределах.
10. Дайте определение непрерывности функции в точке.
11. Укажите основные свойства непрерывных функций.
12. Сформулируйте определение производной.
13. Каков геометрический смысл производной?
14. Что называется касательной к кривой? Напишите уравнение касательной к графику функции y = f (x).
15. Каков механический смысл первой и второй производной?
16. Каковы правила вычисления производных суммы, произведения и частного двух функций?
17. Сформулируйте правило вычисления производной сложной функции.
18. Что называется дифференциалом функции?
19. Каковы признаки возрастания и убывания функций?
20. Сформулируйте правила нахождения экстремумов функции.
21. Приведите пример, показывающий, что обращение в нуль производной не является достаточным условием экстремума функции.
22. Как найти интервалы выпуклости, вогнутости, точки перегиба кривой?
23. Дайте определение асимптоты кривой. Как найти вертикальные и наклонные асимптоты графика функции?
Тема VIII. Интегральное исчисление функции
одной переменной
Прежде чем приступить к интегрированию функций, тщательно изучите таблицу интегралов, свойства определенного интеграла и два простейших метода интегрирования: метод замены переменной и способ подстановки. Успех интегрирования в значительной степени зависит от того, сумеем ли мы подобрать удачную замену переменной, упрощающую данный интеграл.
При использовании метода интегрирования по частям очень важно правильно выбрать множители U и dv. Хотя общих правил разбиения нет, тем не менее можно руководствоваться некоторыми частными правилами. Например, если подынтегральная функция представляет собой произведение показательной или тригонометрической функции и многочлена, то в качестве множителя U следует выбирать многочлен. Если же подынтегральная функция является произведением логарифмической или обратной тригонометрической функций и многочлена, то в качестве множителя U следует выбрать логарифмическую или обратную тригонометрическую функцию.
При интегрировании выражения, содержащего в знаменателе квадратный трехчлен, целесообразно привести этот трехчлен к виду с выделенным полным квадратом.
При решении задач на вычисление площадей фигур, ограниченных линиями у = f( x ), у = g ( x ) (f(x) ≥g(x)) и прямыми х = а, х = b, следует пользоваться формулой
S = 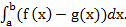
При этом данная формула остается верной при любых знаках значений функций 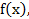 g(х).
g(х).
Пример:
1) Найти интеграл ∫(5 − 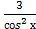 +2
+2 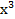 )dх.
)dх.
Воспользуемся таблицей интегралов и основными свойствами первообразной
∫(5 − 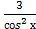 +2
+2 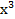 )dх = 5∫dх − 3∫
)dх = 5∫dх − 3∫ 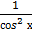 dх+2∫
dх+2∫ 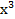 dх =
dх =
= 5х − 3tgх + 2 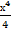 +с = 5х −3tgх +
+с = 5х −3tgх + 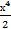 +с.
+с.
2) Найти интеграл ∫ 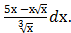
Воспользуемся определением степени с дробным показателем ( 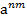 =
= 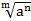 , а > 0), правилами действий со степенями с одинаковыми основаниями (аn am = an+m,
, а > 0), правилами действий со степенями с одинаковыми основаниями (аn am = an+m, 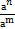 =
= 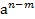 ), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно.
), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно.
∫ 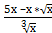 dх = ∫
dх = ∫ 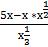 dх= ∫
dх= ∫ 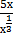 dх − ∫
dх − ∫ 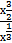 dх =
dх =
= 5∫х  dх − ∫х
dх − ∫х  dх = 5
dх = 5  −
− 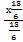 +с = 3
+с = 3 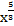 −
− 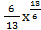 +с =
+с =
= 3* 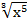 −
− 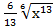 +с.
+с.
3) Найти интеграл
∫ 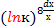 .
.
Применим подстановку t = 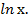
Тогда dt = 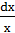 .
.
Имеем ∫ ( 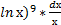 = ∫
= ∫ 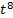 dt =
dt = 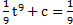 (
( 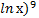 + c.
+ c.
4) Найти интеграл
∫ 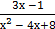 dх.
dх.
Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:
х2 − 4х + 8 = х2 + 4 +7 = (х − 2)2 + 22.
Тогда после подстановки t = х − 2 получаем:
∫ 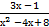 dх = ∫
dх = ∫ 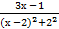 dх =∫
dх =∫ 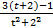 dt = ∫
dt = ∫ 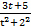 dt =
dt =
= ∫ 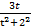 dt +∫
dt +∫ 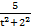 dt =
dt = 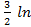 (t2+4) +
(t2+4) +  actg
actg  +c =
+c =
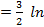 (х − 2
(х − 2 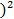 +4) +
+4) + 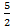 actg
actg 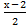 +c =
+c =
= 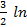 (х2 − 4х +8) +
(х2 − 4х +8) +  actg
actg 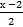 + с.
+ с.
При этом при вычислении интеграла ∫ 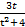 dt мы воспользовались заменой переменной z = t2 +4.
dt мы воспользовались заменой переменной z = t2 +4.
Тогда dz = 2tdt, откуда
∫ 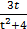 dt =
dt = 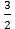 ∫
∫ 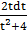 =
= 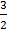 ∫
∫  =
= 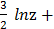 c =
c = 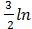 (
( 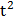 +4) +c.
+4) +c.
5) Найти интеграл
∫(2х + 8)* 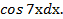
Применим формулу интегрирования по частям
∫udv = uv − ∫vdu.
Положим u = 2х +8, dv = 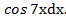
Тогда du = 2dх, v = ∫ 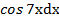 =
= 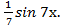
Следовательно,
∫(2х + 8) 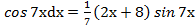 −
− 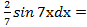
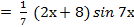 +
+ 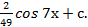
6) Найти интеграл
∫actg3х*dх.
Положим u = actg3х, dv = dх,
тогда du = 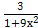 , v = х.
, v = х.
Отсюда
∫actg3хdх = х* actg3х −3∫ 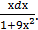
Применим в последнем интеграле подстановку t = 1+9 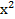 , получим dt = 18хdх, следовательно,
, получим dt = 18хdх, следовательно,
3∫ 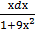 =
= 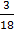 ∫
∫ 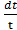 =
= 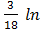 (1+9
(1+9 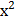 )+с.
)+с.
Отсюда
∫actg3хdх = х* actg3х − 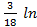 (1+9
(1+9 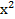 )+с.
)+с.
7) Вычислить площадь фигуры ограниченной параболами
y = 2х2 – х – 2;
y = -х2 + х −1.
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части:
2х2 – х − 2 = -х2 + х − 1
3х2 – 2х −1= 0
Д = 4 + 4*3 = 16
х1 = 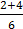 =1; х2 =
=1; х2 = 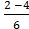 = -
= -  .
.
Вычисление площади осуществляем по формуле
S = 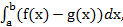
где f(х), g(х) – 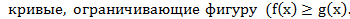
В нашем случае
S = 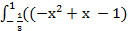 − (2х2 − х – 2))
− (2х2 − х – 2)) 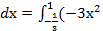 + 2х + 1)
+ 2х + 1)
dх = (-3  + 2
+ 2 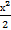 + х)
+ х) 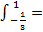
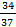 (ед2).
(ед2).
у = 2х2 – х −2
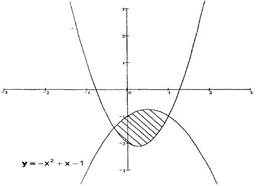
Ответ: S = 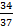 ед2.
ед2.
Контрольная работа №3
I. Найдите интегралы:
1) a) ∫(2 − 3 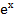 + х)dх б) ∫
+ х)dх б) ∫ 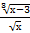 dх
dх
2) а) ∫(3 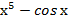 −1)dх б) ∫
−1)dх б) ∫ 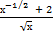 dх
dх
3) а)∫(7 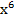 −
− 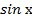 + 3)dх б) ∫
+ 3)dх б) ∫ 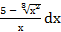
4) а) ∫(7 − 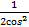 –
– 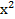 )dх б) ∫
)dх б) ∫ 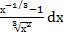
5) а)∫( 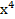 −
− 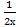 −4)dх б)∫
−4)dх б)∫ 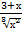 dх
dх
6) а)∫(3 − 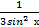 +2)dх б) ∫
+2)dх б) ∫ 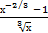 dх
dх
7) а)∫(3 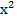 −
− 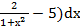 б) ∫
б) ∫ 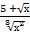 dх
dх
8) а)∫(х − 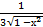 +2)dх б) ∫
+2)dх б) ∫ 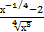 dх
dх
9) а)∫(2 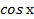 −5
−5 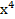 +3)dх б) ∫
+3)dх б) ∫ 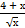 dх
dх
10) а)∫(5 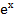 −
− 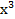 −4)dх б) ∫
−4)dх б) ∫ 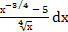
11) а)∫ 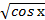 ∗
∗ 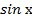 dх б) ∫
dх б) ∫ 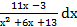
в) ∫ 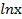 dх
dх
12) а) ∫ 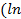 х)3
х)3 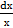 б) ∫
б) ∫ 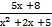
в) ∫(2х +1)∗ 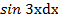
13) а) ∫ 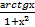 dх б) ∫
dх б) ∫ 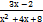
в)∫(х −1)∗ 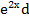 х
х
14) а) ∫ 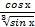 dх б) ∫
dх б) ∫ 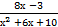
в)∫х ∗ 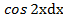
15) а) ∫ 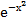 хdх б)∫
хdх б)∫ 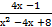
в) ∫ 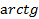 2хdх
2хdх
16) а) ∫ 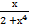 dх б)∫
dх б)∫ 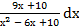
в) ∫(5х +1)∗ 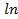 хdх
хdх
17) а) ∫ 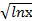 ∗
∗ 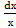 б) ∫
б) ∫ 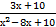 dх
dх
в)∫(8х −2)∗ 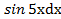
18) а) ∫ 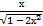 dх б)∫
dх б)∫  dх
dх
в) ∫(х −3)∗ 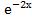 dх
dх
19) а)∫ 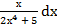 б) ∫
б) ∫ 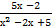 dх
dх
в) 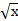 ∗
∗ 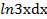
20) а)∫ 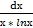 б)∫
б)∫ 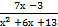 dх
dх
в) ∫(2х +8)∗ 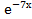 dх.
dх.
II. Вычислите площадь фигуры, ограниченной заданными параболами:
21) у = 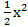 –х + 1; 22) у =
–х + 1; 22) у = 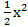 + х +2;
+ х +2;
у = 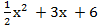 у =
у = 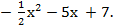
23) у = 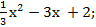 24) у = 2х2 +6х −3
24) у = 2х2 +6х −3
у = 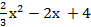 у =
у = 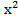 +х+5
+х+5
25) у = 3 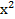 −5х −1; 26) у =
−5х −1; 26) у = 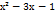
27) у = 2 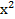 – 6х + 1 28) у =
– 6х + 1 28) у = 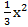 −2х + 4
−2х + 4
у =- 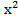 + х −1 у = −-
+ х −1 у = −- 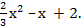
29) у = 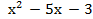 30) у =
30) у = 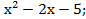
у =-3 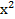 +2х −1. у =-
+2х −1. у =- 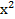 – х +1.
– х +1.
Вопросы для самоконтроля
1. Сформулируйте определение первообразной.
2. Каковы основные свойства неопределенного интеграла?
3. Выведите формулу интегрирования по частям.
4. Что называется интегральной суммой данной функции y= f(x) на данном отрезке 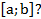
5. Дайте определение определенного интеграла.
6. Каков геометрический смысл определенного интеграла от заданной функции?
7. Перечислите основные свойства определенного интеграла.
8. Напишите формулу Ньютона-Лейбница.
9. В чем состоит способ подстановки для вычисления определенного интеграла?
10. Как выглядит формула интегрирования по частям для определенного интеграла?
Тема IX . Геометрические тела и их поверхности
В этой теме изучаются геометрические тела: призма, параллелепипед, пирамида −полная и усеченная, цилиндр, конус − полный и усеченный, шар и его части.
Особое внимание следует обратить на различия между прямой, наклонной и правильной призмами; между наклонным, прямым и прямоугольным параллелепипедами. При изучении пирамиды и ее свойств помните, что если ребра пирамиды равнонаклонны, то ее вершина проектируется в центр окружности, описанной около основания; если же грани пирамиды равнонаклонны, то ее вершина проектируется в центр окружности, вписанной в основание пирамиды. Обратите внимание на свойства, присущие только правильной пирамиде.
Необходимо учесть, что цилиндр, конус и шар являются телами вращения.
Если осевое сечение цилиндра квадрат, то цилиндр является равносторонним. Если осевое сечение конуса равносторонний треугольник, то конус является равносторонним. Необходимо знать, что все сечения шара круги, а сферы - окружности.
В задачах обязательно сделать рисунок с кратким условием. Следует учесть, что решение задач по стереометрии сводится к решению планиметрических задач.
Примеры:
1) В прямом параллелепипеде стороны основания равны 3 и 5 см, а одна из диагоналей основания 4 см. Меньшая диагональ параллелепипеда составляет с плоскостью основания угол 60°.
Определить диагонали параллелепипеда.
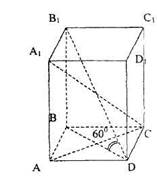
Дано: А…D1 – прямой параллелепипед
АВ=5 см
ВС=3 см
ВD=4 см
∠ВDВ1 =60◦
Найти: А1С.
В1D
Решение
Так как 42 < 52 + З2, то BD − меньшая диагональ основания.
Из ∆DBB следует, что
В1D = 4*2 = 8 см
ВВ1 =DD1 = 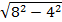 =
= 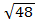 = 4
= 4 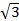 см.
см.
Из параллелограмма ABCD имеем
AC2 + BD2 =2AB2 + 2BC2 = 50 + 18 = 68
АС2 = 68 − ВD2 = 68−16 = 52 см2 .
Из ∆AA1C no теореме Пифагора
A1C = 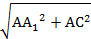 =
= 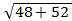 =
= 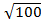 = 10 см.
= 10 см.
Ответ: В1D = 8 см; А1С = 10 см.
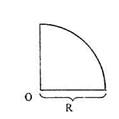
2) Четвертая часть круга, имеющего радиус 12 см, свернута в коническую поверхность. Найти радиус основания конуса
|
|
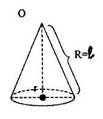
Дано О - центр четверти круга
R=12 см.
Найти г.
Решение: 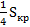 =
= 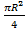 =
= 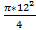 = 36
= 36 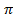 cм2.
cм2.
S бок. конуса =  Sкруга =36
Sкруга =36 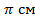 2.
2.
Образующая конуса 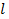 = R = 12 cм.
= R = 12 cм.
S бок. конуса = 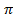 ∗r∗
∗r∗ 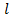 = 36 см2.
= 36 см2.
r 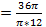 = 3 cм.
= 3 cм.
Ответ: r = 3 cм.
Тема x. Объемы и площади поверхностей
геометрических тел
Вычисляя площади поверхностей геометрических тел по стандартным формулам, необходимо помнить, что для многогранников площадь боковой поверхности можно вычислить как сумму площадей всех боковых граней
При вычислении объемов геометрических тел следует знать, что отношение объемов подобных тел равно отношению кубов их линейных размеров. Геометрические тела, объемы которых равны, называются равновеликими.
К задачам необходимо делать рисунок с кратким условием. При верном изображении данного геометрического тела любая задача стереометрии сводится к решению планиметрической задачи. Примеры:
1. Сторона основания правильной шестиугольной призмы равна 3 см, а ее боковая поверхность 54 см2. Вычислить объем призмы.
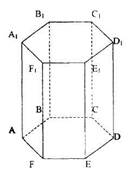
Дано: А…F1 – правильная шестиугольная призма
АB = 3 см
Sбок = 54 см2
Найти Vпризмы.
Решение:
V призмы = Sосн ∗H
Sбок = Росн ∗Н 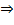 Н=
Н= 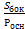
Н = 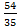 =3 см.
=3 см.
Sосн =  AB2 ∗
AB2 ∗ 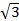 =
= 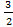 ∗9 ∗
∗9 ∗ 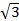 =
= 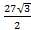 см2
см2
Vпризмы = 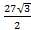 ∗3 = 40,5 ∗
∗3 = 40,5 ∗ 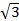 см2.
см2.
2. Основанием прямой призмы служит треугольник со сторонами 6, 8 и 10 см. Высота призмы 24 см. Найти поверхность и объем описанного шара
|
|
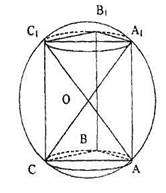 Дано: О - центр описанного шара
Дано: О - центр описанного шара
А. .. С1 − прямая призма
АВ = 6 см.
ВС = 8 см.
АС =10 см
AA1= 24 см
Найти: Sшара, Vшара
Решение
Так как 102 = 82 + 62, следовательно, ∆АВС - прямоугольный. Точка О − середина диагонали прямоугольника AA1C1С.
A1C = 2R = 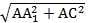
2R= 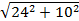 =
= 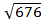 = 26 см.
= 26 см.
К = 13 см.
Sшapa = 4𝜋R2 = 4𝜋 * 169 = 626𝜋 cм2
Vшapa = 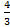 𝜋R3 =
𝜋R3 = 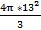 =4262 ∗
=4262 ∗ 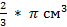
Ответ: 8шара = 626𝜋 см2; Vшара = 4262 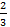 * 𝜋 см3.
* 𝜋 см3.
Контрольная работа № 4
1. Найти диагональ прямоугольного параллелепипеда, стороны основания которого равны 3 и 4 см, если она образует с плоскостью основания угол 600.
2. В прямом параллелепипеде ребра, выходящие из одной вершины, равны 1, 2 и 3 см, причем два меньших образуют угол в 60°. Вычислить диагонали параллелепипеда.
3. В правильной треугольной призме каждое ребро равно 4 см. Через боковое ребро и ось призмы проведена плоскость. Вычислить площадь сечения.
4. В правильной треугольной призме, каждое ребро которой равно 6 см, через сторону основания и середину оси про ведена плоскость. Вычислить площадь сечения.
5. Сторона основания правильной треугольной пирамиды 9 см, а боковое ребро 6 см. Найти высоту пирамиды.
6. Боковое ребро правильной треугольной пирамиды 4 см и образует с плоскостью основания угол 30°. Найти площадь основания пирамиды.
7. Высота правильной четырехугольной пирамиды 7 см, а сторона основания 8 см. Найти боковое ребро.
8. В правильной треугольной призме через сторону основания проведено сечение под углом 30° к плоскости основания. Получился треугольник, площадь которого 8см2. Найти сторону основания призмы.
9. Найти длину бокового ребра правильной четырехугольной призмы, если ее диагональ равна 7  см и составляет с боковой гранью угол 30°.
см и составляет с боковой гранью угол 30°.
10. В правильной четырехугольной пирамиде плоскость сечения, параллельного основанию, разделила высоту по полам. Найти сторону основания пирамиды, если площадь сечения равна 36 см2.
11. Высота конуса 8 см, образующая 10 см. Найти радиус вписанного шара.
12. Высота конуса 4 см, образующая 5 см. Найти радиус вписанного шара.
13. Высота конуса 2 см, образующая 4 см. Найти радиус описанного шара.
14. Высота конуса 3 см, образующая 6 см. Найти радиус описанного шара.
15. В шар вписан конус. Найти высоту конуса, если радиус шара 5 см, а радиус основания конуса 4 см.
16. В шар вписан конус. Найти высоту конуса, если радиус шара 10 см, а радиус основания конуса 8 см.
17. Конус вписан в шар, радиус которого 17 см. Найти радиус основания конуса, если угол при вершине его осевого сечения равен 30°.
18. Высота конуса 20 см, образующая 25 см. Найти радиус вписанного полушара, основание которого лежит на основании конуса.
19. Высота конуса 10 см, образующая 26 см. Найти радиус вписанного полушара, основание которого лежит на основании конуса.
20. Шар, диаметр которого 34 см, описан около конуса. Угол при вершине осевого сечения конуса равен 30°. Найти диаметр основания конуса.
21. а) В усеченном конусе высота равна 12 см. Образующая конуса перпендикулярна диагонали осевого сечения конуса и образует с плоскостью большего основания угол в 60°. Вычислить его боковую поверхность.
б) Измерения прямоугольного параллелепипеда равны 12, 15 и 16 см. Вычислить объем куба, полная поверхность которого равна боковой поверхности данного параллелепипеда.
22. а) В прямом параллелепипеде стороны оснований равны 10 и 17 см. Одна из диагоналей основания равна 21 см. большая диагональ параллелепипеда равна 29 см. Вычислить боковую поверхность параллелепипеда.
б) Объем усеченного конуса равен 248𝜋 см3, высота равна 8 см., а радиус верхнего основания − 4 см. Вычислить радиус другого основания конуса.
23. а) В наклонной треугольной призме расстояние между боковыми ребрами равны 7, 8 и 12 см. Боковое ребро равно 14 см. Вычислить боковую поверхность призмы.
б) Осевое сечение цилиндра - квадрат, диагональ которого равна 8  см. Вычислить объем и боковую поверхность цилиндра.
см. Вычислить объем и боковую поверхность цилиндра.
24. а) В основании наклонной призмы лежит параллелограмм со сторонами 6 и 12 см и острым углом 60°. Боковое ребро призмы равно 14 см и составляет с плоскостью основания угол 30°. Вычислить объем призмы.
б) высота конуса равна 12 см и составляет с его образующей угол 45°. Вычислить объем конуса.
25.а) В наклонной призме стороны основания равны 4, 13 и 15 см. Боковое ребро равно 10 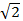 см и наклонено к плоскости основания под углом 45°. Вычислить объем призмы.
см и наклонено к плоскости основания под углом 45°. Вычислить объем призмы.
б) В полном конусе площадь основания равна 16𝜋 см2, площадь осевого сечения 8 см2. Вычислить объем конуса.
26.а) Вычислить объем правильной шестиугольной пирамиды, сторона основания и боковое ребро которой соответственно равны 9 и 15 см.
б) Поверхность шара равна 113,04 дм. Вычислить его объем.
27.а) Основанием пирамиды служит прямоугольник со сторонами 6 и 15 см. Высота пирамиды проходит через точку пересечения диагоналей основания, боковая поверхность пирамиды равна 126 см2. Вычислить её объем.
б) Через середину радиуса шара перпендикулярно к нему проведена плоскость. Площадь сечения равна 18, 84 см2. Вычислить поверхность шара.
28.а) Ребро куба равно 6 см. Определить высоту равновеликой ему призмы, площадь основания которой 56 см2.
б) Радиус оснований усеченного конуса и его высота относятся как 3:6:4. Вычислить боковую поверхность конуса, если его образующая равна 25 см.
29. а) Вычислить объем треугольной призмы, основанием которой является прямоугольный треугольник с катетами 12 и 16 см, а боковое ребро равно гипотенузе треугольника основания.
б) Образующая полного конуса равна 18 см и составляет с его осью угол 45°. Вычислить объем конуса.
30.а) В правильной четырехугольной пирамиде сторона основания равна 30 см, а высота 20 см. Найти объем усеченной пирамиды, отсекаемой от данной плоскостью, параллельной её основанию и отстоящей от него на 5 см.
б) Высота цилиндра на 10 см больше его радиуса основания. Вычислить объем цилиндра, если его полная поверхность равна 144𝜋 см2.
31. Треугольник со сторонами 6, 8 и 10 см вращается вокруг средней стороны. Вычислить поверхность и объем тела вращения.
32. Прямоугольная трапеция вращается вокруг оси, перпендикулярной основанию трапеции и проходящей через вершину её острого угла. Вычислить объем тела вращения, если основания трапеции равны 4 и 7 см, а большая боковая сторона 5 см.
33. Треугольник со сторонами 8, 6 и 10 см вращается вокруг большей стороны. Вычислить объем тела вращения.
34. Равнобедренная трапеция с острым углом в 30° вращается вокруг оси, проходящей через её боковую сторону. Вычислить поверхность тела вращения, если основания и боковая сторона трапеции соответственно равны 6, 20 и 14 см.
35. Равносторонний треугольник со стороной 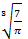 вращается вокруг одной из сторон. Найти объем полученного тела вращения.
вращается вокруг одной из сторон. Найти объем полученного тела вращения.
36. Правильный треугольник со стороной 4 см вращается вокруг стороны. Найти объем тела вращения.
37. Ромб с диагоналями 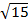 и
и 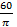 см вращается вокруг большей
см вращается вокруг большей
диагонали. Найти объем тела вращения.
38. Равносторонний треугольник вращается вокруг своей стороны равной 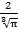 см. Найти объем тела вращения.
см. Найти объем тела вращения.
39. Квадрат со стороной 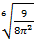 см вращается вокруг диагонали. Найти объём тела вращения.
см вращается вокруг диагонали. Найти объём тела вращения.
40. Равнобедренная трапеция с острым углом 60° вращается вокруг оси, проходящей через середины её оснований. Вычислить поверхность тела вращения, если основания трапеции 6 и 2 см.
Вопросы для самоконтроля
1. Дайте определения многогранника.
2. Перечислите виды многогранников.
3. Какими свойствами обладают грани и диагонали параллелепипеда?
4. Всегда ли четырехугольная призма будет параллелепипедом?
5. Сформулируйте свойство сечений пирамиды плоскостью, параллельной её основанию.
6. Дайте определения цилиндрической и конической поверхностям.
7. Дайте определения цилиндра, конуса, усеченного конуса, шара.
8. Выпишите формулы боковых и полных поверхностей многогранников и тел вращения.
Математика
Методические указания, рабочая программа и контрольные задания для студентов-заочников I и II курсов на базе
9 классов Челябинского монтажного колледжа
МАТЕМАТИКА
Методические указания, рабочая программа и контрольные задания для студентов-заочников I и II курсов на базе
9 классов Челябинского монтажного колледжа
Челябинск 2010

Составитель: Смирнова Л.Л. преподаватель математики Челябинского монтажного колледжа
Пояснительная записка
Данное пособие ставит своей целью оказание помощи студенту-заочнику в организации его самостоятельной работы по овладению системой знаний, умений и навыков в объеме действующей программы.
Прежде чем приступить к выполнению контрольных заданий, необходимо повторить курс математики неполной средней школы, уделить особое внимание правилам действий над дробями, пропорциями, процентами, преобразованиям алгебраических выражений, повторить сведения о функциях и числовых последовательностях в объеме школьной программы. Необходимо познакомиться с принятой математической символикой. Для повторения рекомендуются учебники для школ и техникумов.
В соответствии с учебным планом студенты-заочники по курсу «Математика» выполняют четыре контрольные работы, сдают один зачет (1-й курс, летняя сессия) и один экзамен (2-й курс, летняя сессия).
Каждое контрольное задание имеет 10 вариантов. Вариант контрольной работы выбирается по последней цифре личного дела (шифра) студента-заочника. Номера задач для контрольных работ указаны в таблице.
При выполнении контрольной работы надо соблюдать следующие правила:
1. Каждая работа выполняется в отдельной тетради, на обложке которой указывается название предмета, номер работы, номер варианта, фамилия, имя, отчество и шифр студента-заочника.
2. Контрольная работа должна быть написана чернилами, аккуратно и разборчиво. Для замечаний должны быть оставлены поля 3 - 4 см. Чертежи выполняются с помощью чертежных инструментов. Замечания рецензента исправлять и стирать нельзя.
3. Условие задачи необходимо записывать полностью. К геометрическим задачам нужно также делать краткую запись условия.
4. Решения задач должны сопровождаться краткими, но достаточными объяснениями. Для решения задачи использовать необходимые вычислительные средства (М.К., справочник и т.д.).
5. Проверенные работы сохраняются и представляются на экзамене.
6. Если работа не зачтена, то ее нужно переделать заново и сдать на повторную рецензию.
7. Несмотря на то, что в пособии даются разъяснения и указания, основной материал следует изучать по учебникам.
| Номер варианта | К. р. № 1 | K.р. | № 2 | К. р. № 3 | К. р. № 4 | |
| 1 | 1, | 11, 21 | 1, 11, | 21, 31 | 1, 11, 21 | 1, 11, 21, 31 |
| 2 | 2, | 12, 22 | 2, 12, | 22, 32 | 2, 12, 22 | 2, 12, 22, 32 |
| 3 | 3, | 13, 23 | 3, 13, | 23, 33 | 3, 13, 23 | 3, 13, 23, 33 |
| 4 | 4, | 14, 24 | 4, 14, | 24, 34 | 4, 14, 24 | 4, 14, 24, 34 |
| 5 | 5, | 15, 25 | 5, 15, | 25, 35 | 5, 15, 25 | 5, 15, 25, 35 |
| 6 | 6, | 16, 26 | 6, 16, | 26, 36 | 6, 16, 26 | 6, 16, 26, 36 |
| 7 | 7, | 17, 27 | 7, 17, | 27, 37 | 7, 17, 27 | 7, 17, 27, 37 |
| 8 | 8, | 18, 28 | 8, 18, | 28, 38 | 8, 18, 28 | 8, 18, 28, 38 |
| 9 | 9, | 19, 29 | 9, 19, | 29, 39 | 9, 19, 29 | 9, 19, 29, 39 |
| 0 | 10 | 10, 20, 30 | 10, 20, 30, 40 | 10, 20, 30 | 10, 20, 30, 40 | |
Литература
1. Зайцев И.Л. Элементы высшей математики - М.: Наука, 1994.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Т. 1,2, - М.: Наука, 1993.
3. Андреев П.П. и др. Геометрия. - М.: Наука, 1998.
4. Данко П.Е. и др. Высшая математика в упражнениях и задачах. -М.: Высшая школа, 2005. - .
5. Клопский В.М. и др. Геометрия. - М.: Просвещение, 1999.
Тематический план курса «Математика»
| № |
Темы
Разделы и темы
Максимальная нагрузка
студента
Количество аудиторных часов при заочной форме обучения
Самостоя-тельная работа студента
Всего
В том числе
|
№ Темы |
Разделы и темы |
Макси- Мальная нагрузка студента | Дата: 2018-12-21, просмотров: 459. | ||