1. Размещением из n различных элементов по m элементов (m<n) называется соединение, которое отличается либо составом, либо порядком своих элементов.
Например, выпишем все размещения из элементов a, b, c, d по два элемента: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.
Для любого натурального числа n произведение 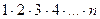 обозначается n!
обозначается n!
читается n-факториал.
Формула для подсчета числа размещений: 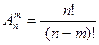
Задача: Найти количество всех двузначных чисел, состоящих из чисел 1,2,3,...,9.
Решение: Это задача о размещении из 9 элементов по 2 элемента, т.к. любые двузначные числа отличаются либо составом цифр, либо их порядком.
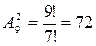
2. Сочетанием из n различных элементов по m элементов (m<n) называется соединение, которое отличается только составом своих элементов.
Например, выпишем вес сочетания из элементов a,b,c,d,e по три элемента: abe, abd, abe, acd, ace, ade, bcd, bce, bde, cde.
Формула для подсчета числа сочетаний: 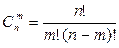
Задача: Дано 5 различных чисел a, b, c, d, e. Сколько можно составить всевозможных произведений из этих чисел, состоящих из двух различных множителей?
Решение: Это задача о числе сочетаний из 5 элементов по 2 элемента, т.к. произведения отличаются только составом множителей 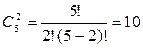
3. Перестановками из n различных элементов называются всевозможные соединения из этих n элементов, т.е. соединения, каждое из которых содержит n различных элементов, взятых в определённом порядке.
Например, все перестановки из элементов a,b,c: abc, acb, bac, bca, cab, cba.
Формула для подсчета числа перестановок: Рп = n!
Задача: На столе находятся 5 различных геометрических фигур, (круг, треугольник, квадрат, ромб, прямоугольник). Сколькими способами можно разложить эти фигуры в один ряд?
Решение: Это задача о числе перестановок из 5 элементов. Р5 = 5!= 120.
К основным понятиям теории вероятности относятся: испытание, событие, вероятность. Испытание – реализация комплекса условий, в результате которого непременно произойдет какое-либо событие. Например, бросание монеты – испытание; появление герба или цифры – события.
Случайным событием называется событие, которое при осуществлении испытания может произойти, а может и не произойти. Например, выстрел по цели — это опыт, случайные события в этом опыте – попадание в цель или промах.
Событие называется достоверным, если в результате опыта оно непременно должно произойти, и невозможным, если оно заведомо не произойдет. События называются несовместными, если ни какие два из них не могут появиться вместе. Например, попадание и промах при одном выстреле – это несовместные события.
Несколько событий образуют полную систему событий, если в результате опыта непременно должно произойти хотя бы одно из них. Например, при бросании игральной кости события, состоящие в выпадении одного, двух, трех, четырех, пяти и шести очков, образуют полную систему событий.
События называются равновозможными, если ни одно из них не является более возможным, чем другие. Например, при бросании монеты выпадение герба или числа - события равновозможные.
Каждое событие обладает какой-то степенью возможности. Числовая мера степени объективной возможности события - это вероятность события. Вероятность события А обозначается Р(А).
Пусть из системы n несовместных равновозможных исходов испытания m исходов благоприятствуют событию А. Тогда вероятностью события А называют отношение m числа исходов, благоприятствующих событию А, к числу n всех исходов данного испытания: P(A)=m/n.
Если В – достоверное событие, то Р(В)=1; если С – невозможное событие, то Р(С)=0, если А – случайное событие, то 0<Р(А)<1.
Задача. Игральную кость подбрасывают один раз. Найти вероятность появления четного числа очков.
Решение. Опыт имеет шесть равновозможных независимых исходов (появление одного, двух, трех, четырех, пяти и шести очков), образующих полную систему. Событию благоприятствуют три исхода (появление двух, четырех и шести очков), поэтому Р(А)=3/6=1/2
При вычислении вероятности часто приходится использовать формулы комбинаторики.
Случайной называется величина, которая в результате опыта может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Пример 1. Число выпавших «гербов» при пятикратном бросании монеты.
Пример 2. Дальность полета артиллерийского снаряда.
Пример 3. Число мальчиков, родившихся в течении суток
Пример 4. Прирост веса домашнего животного за месяц.
Случайные величины будем обозначать заглавными буквами латинского алфавита X, Y, Z, а их возможные значения – малыми буквами x, y, z.
Пример 5. Х – число шахматных партий, окончившихся ничейным результатом, из трех сыгранных. В этом случае величина Х может принять следующие значения: х1=0, х2=1, х3=2, х4=3.
Дискретной случайной величиной (ДСВ) называют такую случайную величину, множество возможных значений которой либо конечное, либо бесконечное, но счетное.
Например, ДСВ – число учащихся, опрошенных на уроке; число солнечных дней в году и т.д.
Непрерывной случайной величиной (НСВ) называют такую случайную величину, которая может принять любое значение из некоторого конечного или бесконечного интервала.
Например, время безаварийной работы станка; расход ГСМ на единицу расстояния; выпадение осадков в сутки и т.д.
Законом распределения ДСВ Х называется всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими вероятностями.
Способы задания закона распределения:
1) для ДСВ – табличный и графический;
например,
| X | x1 | x2 | … | xi | … | xn |
| P | p1 | p2 | … | pi | … | pn |
Табличный ряд распределения, где x1; x2; …; xi; …; xn образуют полную группу, а
p1+p2+…+pi+…+pn=1
2) для НСВ – можно задать так же, как функцию одной переменной, используя табличный, графический или аналитический способ задания.
В тех случаях, когда закон распределения СВ неизвестен, СВ изучают по ее числовым характеристикам. Их назначение – в сжатой форме выразить наиболее важные черты распределения. К числовым характеристикам относится математическое ожидание, дисперсия и т.д.
Математическим ожиданием ДСВ называют сумму произведений всех ее возможных значений на их вероятности и обозначается
М(Х)=x1p1+x2p2+…+xnpn
Математическим ожиданием НСВ Х, возможные значения которой принадлежат отрезку 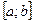 , называется определенный интеграл
, называется определенный интеграл 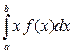 , т.е.
, т.е. 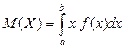
Дисперсией (распределением) ДСВ называют математическое ожидание квадрата отклонения СВ от ее математического ожидания, т.е.
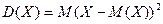 или
или 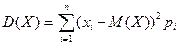
Для НСВ 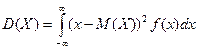
Раздел 4.
Основные численные методы
Приближенное вычисление интеграла.
На практике часто встречаются интегралы, которые не выражаются через элементарные функции или выражаются очень сложно. Нередко подынтегральная функция задается таблицей или графиком. В этих случаях интегралы находят приближенными методами: формулами прямоугольников, формулами трапеций.
Формулы прямоугольников: промежуток интегрирования (а, b ) делим точками
х1,х2,…,х n -1 на n равных частей; длина каждой 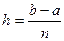 .
.
Формулами прямоугольников называются следующие приближенные равенства:
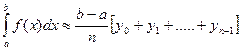 , (1)
, (1)
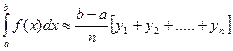 , (2)
, (2)
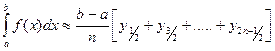 . (3)
. (3)
В большинстве случаев при данном n формула (3) точнее, чем (1) и (2). С увеличением n точность формул (1), (2), (3) неограниченно возрастает.
Предельная погрешность формулы (3) составляет:
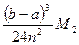 , где М2 - наибольшее значение
, где М2 - наибольшее значение 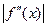 в промежутке (а , b ). Для эмпирических функций М2 берут наибольшее значение величины
в промежутке (а , b ). Для эмпирических функций М2 берут наибольшее значение величины 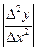 .
.
Пример: Вычислить по формуле (3)на 10 ординат (п=10) приближенное значение интеграла: 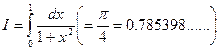 .
.
Решение: 
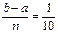 ;
;
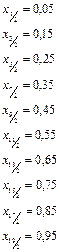
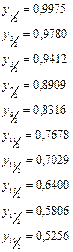
Сумма 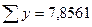
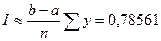 .
.
Погрешность составляет примерно 0,0002.
4. Список вопросов к зачету
- Функция. Предел функции. Замечательные пределы.
2. Производные и дифференциалы функций, заданных различными способами. Правило Лопиталя.
3. Функции нескольких переменных. Область определения.
4. Частные производные функции двух переменных.
5. Неопределенный интеграл. Свойства. Основные методы интегрирования.
6. Определенный интеграл, его свойства.
7. Приложения определенного интеграла для решения геометрических задач.
- Задачи, приводящие к понятию дифференциального уравнения первого порядка.
- Основные понятия и определения теории дифференциального уравнения первого порядка.
- Дифференциальное уравнение с разделёнными переменными, алгоритм решения.
- Дифференциальное уравнение с разделяющимися переменными, алгоритм решения.
- Линейное дифференциальное уравнение первого порядка, алгоритм решения, метод Бернулли.
- Линейное дифференциальное уравнение первого порядка, алгоритм решения, метод Лагранжа.
- Линейное дифференциальное уравнение первого порядка с постоянными коэффициентами, алгоритм решения.
- Задачи, приводящие к понятию дифференциального уравнения второго порядка: различные случаи движения материальной точки.
- Дифференциальные уравнения второго порядка, основные понятия.
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами, алгоритм решения при D>0.
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами, алгоритм решения при D=0.
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами, алгоритм решения при D<0.
- Однородное дифференциальное уравнение первого порядка, алгоритм решения.
21. Что называется множеством? Перечислите способы задания множеств.
- Что называется пересечением множеств? Приведите примеры.
- Что называется объединением множеств? Приведите примеры.
- Что называется разностью множеств? Приведите примеры.
- С помощью кругов Эйлера изобразите отношения между множествами.
- Что называется декартовым произведением множеств?
- Перечислите виды отношений на множестве, их свойства и постройте их графы.
- Каким образом определяется граф?
- Что является путем в графе?
- Как определяется такой вид графа, как дерево?
- Какими способами можно задать граф?
32. Основные понятия комбинаторики. Комбинации перестановки, размещения, сочетания.
33. Бином Ньютона. Свойства биноминальных коэффициентов.
34. События. Виды событий. Определения вероятностей.
35. Теоремы сложения теории вероятностей.
36. Теоремы умножения теории вероятностей.
- Формулы полной вероятности и Баейса..
38. Дискретная случайная величина и её числовые характеристики.
39. Функция распределения дискретной случайной величины.
40. Непрерывные случайные величины. Математическое ожидание и дисперсия непрерывной СВ.
41. Численное интегрирование. Формула прямоугольников.
42. Численное интегрирование. Формула трапеций.
5. Примерные практические задания к зачету
- Найти производную функций: у =
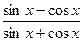 .
. - Найти производную сложной функции: у = ln ctg3x.
- Исследовать функцию на монотонность, экстремумы у =
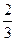 x3-x2 + 4 и построить схематичный график.
x3-x2 + 4 и построить схематичный график.
4. Найти частною производную 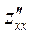 функции z=x2y3+2xy-5ln(x)y
функции z=x2y3+2xy-5ln(x)y
- Найти частные производные функции двух переменных
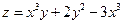
- Скорость прямолинейного движения тела
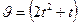 см/с. Найти путь тела, пройденного за 6 с, считая
см/с. Найти путь тела, пройденного за 6 с, считая 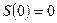 см.
см. - Вычислить интегралы способом замены переменной
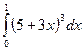
8. Вычислить интегралы способом замены переменной 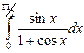
- Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у2=х+2, х=0, х=9 и у=0.
- Имеется два набора деталей. Вероятность того, что деталь первого набора стардартна0,8, второго – 0,9. найти вероятность того, что взятая наугад деталь окажется стандартной.
- В урне имеется 4 шара с номерами от 1 до 4. Вынули два шара. Случайная величина
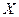 - сумма номеров шаров. Построить ряд распределения случайной величины
- сумма номеров шаров. Построить ряд распределения случайной величины 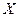 .
. - Бросают три игральные кости. Какова вероятность того, что выпавшие цифры будут попарно различными?
- Решить уравнение:
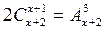
- ДСВ задана рядом распределения. Закончить ряд распределения, найти числовые характеристики:
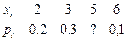
- Построить многоугольник распределения и найти числовые характеристики ДСВ по ряду распределения ..
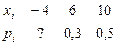
Рекомендуемая литературу
Основные источники:
1. Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А.А. Дадаян. – М.Форум, 2013. - 544 с. - (Профессиональное образование).
2. Математика: Учебное пособие для студентов образовательных учреждений сред. проф. образования/ В.П. Омельченко, Э.В. Курбатова. – 3-е изд., испр. – Ростов н/Д: Феникс, 2013. – 380 с. - (Среднее профессиональное образование).
3. Математика [Текст] : учебник для студентов образоват. учреждений сред. проф. образования / С.Г. Григорьев, С.В.Иволгина; под ред. В.А. Гусева. - 9-е изд., стереотип. - М. : Издательский центр ""Академия"", 2013 . - 416 с. - (Среднее профессиональное образование.) .
4. Математика: учебное пособие для студентов средних специальных учебных заведений/ Н.А. Березина, Е.Л. Максина. – М.: РИОР, 2014. – 175 с. – (Профессиональное образование).
5. Математика [Текст] : учебник для СПО / Н.В. Богомолов, П.И. Самойленко. - 5-е изд., перераб. и доп. - М. : Издательство Юрайт, 2016 . - 396 с. - (Профессиональное образование)
Дополнительные источники:
6. Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А.А. Дадаян. – 2-е изд. – М.: ФОРУМ: ИНФРА-М, 2013. – 552 с. - (Профессиональное образование).
7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. 1: Учеб. Пособие для втузов. – 7-ое изд., испр. – М.: Высш.шк., 2014 – 448 с.: ил.
8. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. 2: Учеб. Пособие для втузов. – 7-ое изд., испр. – М.: Высш.шк., 2014. – 416 с.: ил.
9. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. – 3-е изд. – М.: Айрис –пресс, 2013. – 288 с.: ил.
10. Богомолов Н.В. Практические занятия по математике: Учеб.пособие для техникумов. – М.: Высш. школа, 2013. -495 с., ил.
Интернет-ресурсы:
1. Электронный учебник по математике http://www.dvoika.net
2. Дидактические материалы по математике и информатике. Учителям математики и информатики http://comp-science.narod.ru
3. Лаборатория математики МИОО http://www.metodist.ru
4. Каталог образовательных Интернет-ресурсов http://www.edu.ru
Дата: 2018-12-21, просмотров: 414.