II . Выполнив действия над матрицами, найти матрицу К.
Данные к условию задачи, соответствующие вариантам:
1) 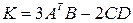 ,
,
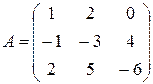 ,
, 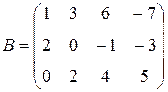 ,
, 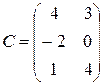 ,
, 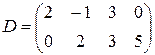 ;
;
2) 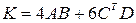 ,
,
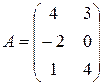 ,
, 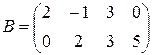 ,
, 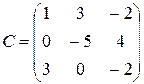 ,
, 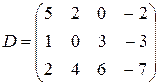 ;
;
3) 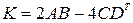 ,
,
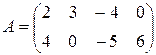 ,
, 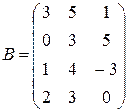 ,
, 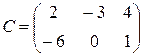 ,
, 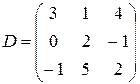 ;
;
4) 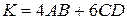 ,
,
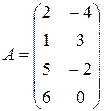 ,
, 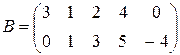 ,
, 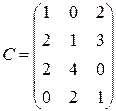 ,
, 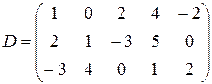 ;
;
5) 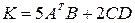 ,
,
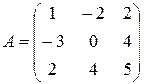 ,
, 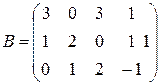 ,
, 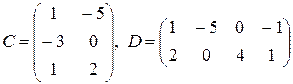 ;
;
6) 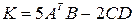 ,
,
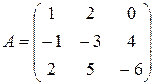 ,
, 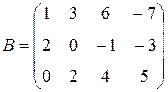 ,
, 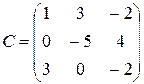 ,
, 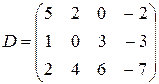 ;
;
7) 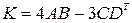 ,
,
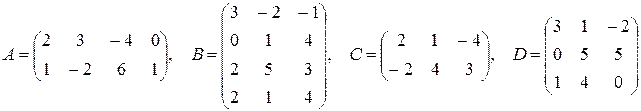 ;
;
8) 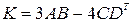 ,
,
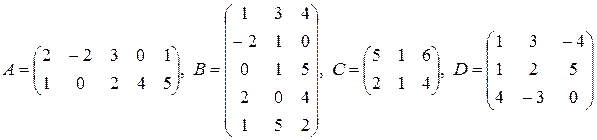 ;
;
9) 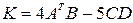 ,
,
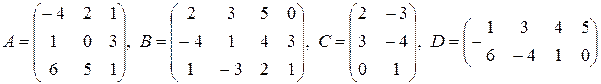 ;
;
0) 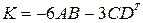 ,
,
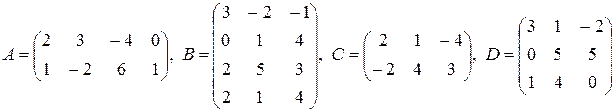 .
.
III . Решить систему:
а) матричным методом (методом обратной матрицы);
б) по формулам Крамера.
Данные к условию задачи, соответствующие вариантам:
1) 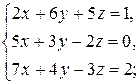
2) 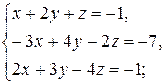
3) 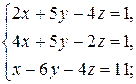
4) 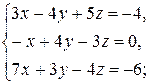
5) 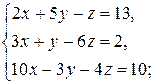
6) 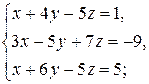
7) 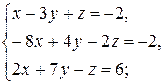
8) 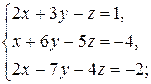
9) 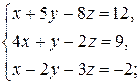
0) 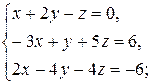
IV . Решить систему линейных уравнений методом Гаусса, найти общее и частное решения, выполнить проверку.
Данные к условию задачи, соответствующие вариантам:
1) 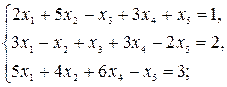
2) 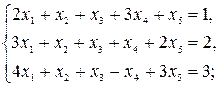
3) 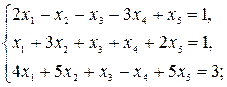
4) 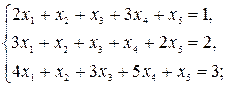
5) 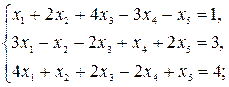
6) 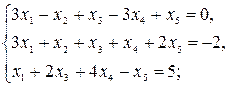
7) 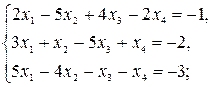
8) 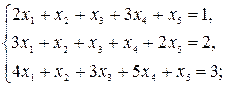
9) 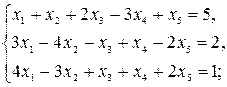
0) 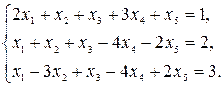
V . Задача. Предприятие выпускает три вида изделий с использованием четырех типов сырья. Нормы затрат сырья на каждое изделие определены матрицей затрат А, себестоимость единицы сырья отражена в матрице С, стоимость доставки единицы сырья каждого типа отражена в матрице D . Найти общие затраты на сырье и общие затраты на транспортировку сырья при плане выпуска продукции, указанном в матрице В
Данные к условию задачи, соответствующие вариантам:
1) 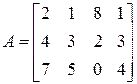 ;
; 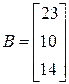 ;
; 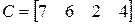 ;
; 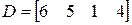 ;
;
2) 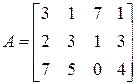 ;
; 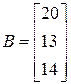 ;
; 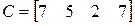 ;
; 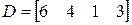 ;
;
3) 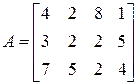 ;
; 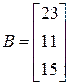 ;
; 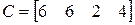 ;
; 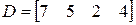 ;
;
4) 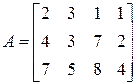 ;
; 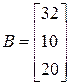 ;
; 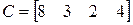 ;
; 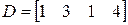 ;
;
5) 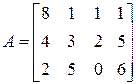 ;
; 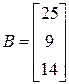 ;
; 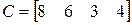 ;
; 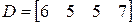 ;
;
6) 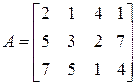 ;
; 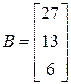 ;
; 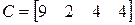 ;
; 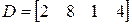 ;
;
7) 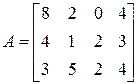 ;
; 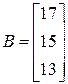 ;
; 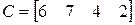 ;
; 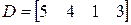 ;
;
8) 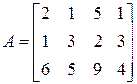 ;
; 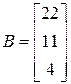 ;
; 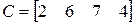 ;
; 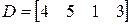 ;
;
9) 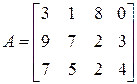 ;
; 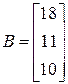 ;
; 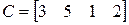 ;
; 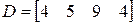 ;
;
0) 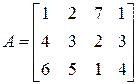 ;
; 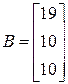 ;
; 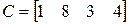 ;
; 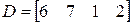 .
.
VI . Задача. Предприятие выпускает три вида продукции, используя сырье трех типов. Расходы каждого типа сырья по видам продукции и запасы сырья на предприятии даны в таблице. Определить объем выпуска продукции каждого вида при заданных запасах сырья.
Данные к условию задачи, соответствующие вариантам:
1)
Тип сырья
Расход сырья по видам продукции, вес.ед./изд.
Запас сырья, вес.ед.
2)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 2 | 4 | 1 | 410 |
| II | 4 | 3 | 4 | 850 |
| III | 1 | 2 | 3 | 390 |
3)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 1 | 4 | 2 | 890 |
| II | 3 | 2 | 3 | 830 |
| III | 2 | 1 | 2 | 510 |
4)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 3 | 1 | 3 | 820 |
| II | 2 | 2 | 3 | 730 |
| III | 3 | 1 | 2 | 610 |
5)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 1 | 5 | 2 | 410 |
| II | 3 | 2 | 3 | 630 |
| III | 2 | 1 | 4 | 550 |
6)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 4 | 2 | 1 | 780 |
| II | 1 | 2 | 2 | 550 |
| III | 3 | 3 | 4 | 1090 |
7)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 1 | 4 | 2 | 380 |
| II | 3 | 2 | 3 | 630 |
| III | 2 | 1 | 2 | 410 |
8)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 2 | 3 | 5 | 1040 |
| II | 3 | 2 | 1 | 650 |
| III | 1 | 1 | 3 | 500 |
9)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 4 | 1 | 5 | 980 |
| II | 2 | 4 | 3 | 990 |
| III | 3 | 5 | 2 | 1130 |
0)
|
Тип сырья |
Расход сырья по видам продукции, вес.ед./изд. |
Запас сырья, вес.ед. | ||
| 1 | 2 | 3 | ||
| I | 4 | 2 | 1 | 610 |
| II | 1 | 2 | 2 | 320 |
| III | 3 | 3 | 4 | 730 |
VII . Даны векторы 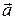 ,
, 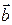 и
и 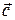 . Необходимо:
. Необходимо:
а) найти модуль векторов 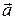 и
и 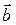 ;
;
б) вычислить угол между векторами 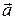 и
и 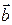 ;
;
в) проверить, будут ли вектора 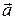 и
и 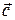 коллинеарны, вектора
коллинеарны, вектора 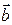 и
и 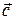 ортогональны;
ортогональны;
г) найти вектор 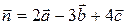 .
.
Данные к условию задачи, соответствующие вариантам:
1) 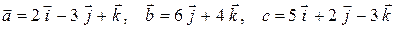 ;
;
2) 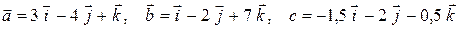 ;
;
3) 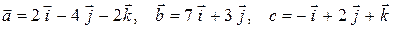 ;
;
4) 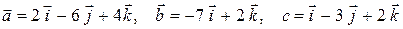 ;
;
5) 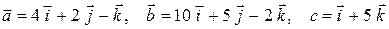 ;
;
6) 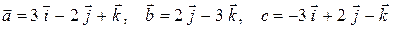 ;
;
7) 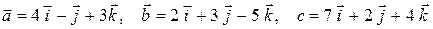 ;
;
8) 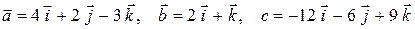 ;
;
9) 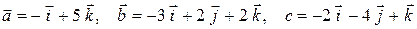 ;
;
0) 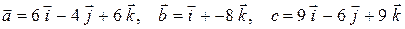 .
.
VIII . Задача. Фиксированные издержки на предприятии при выпуске некоторой продукции составляют F руб. в месяц, переменные издержки – V 0 руб. за единицу продукции, при этом выручка составляет R 0 руб. за единицу изготовленной продукции. Составить функцию прибыли P ( x ) ( x – количество произведенной продукции); построить ее график и определить точку безубыточности.
Данные к условию задачи, соответствующие вариантам:
1) 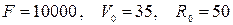 ;
;
2) 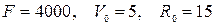 ;
;
3) 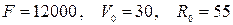 ;
;
4) 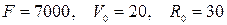 ;
;
5) 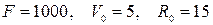 ;
;
6) 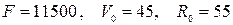 ;
;
7) 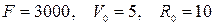 ;
;
8) 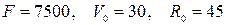 ;
;
9) 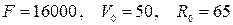 ;
;
0) 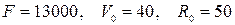 .
.
IX . Частное предприятие планирует выпускать продукцию двух видов  и
и  , для производства которой необходимо сырье трех типов. Предприятие обеспечено сырьем каждого типа соответственно в количестве:
, для производства которой необходимо сырье трех типов. Предприятие обеспечено сырьем каждого типа соответственно в количестве:  ,
, 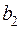 ,
, 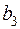 кг. На изготовление единицы изделия первого вида требуется израсходовать сырья каждого типа соответственно в количестве:
кг. На изготовление единицы изделия первого вида требуется израсходовать сырья каждого типа соответственно в количестве: 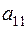 ,
, 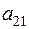 ,
, 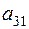 кг., на единицу изделия второго вида –
кг., на единицу изделия второго вида – 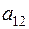 ,
, 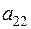 ,
, 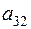 кг. Прибыль от реализации единицы изделия первого вида составляет
кг. Прибыль от реализации единицы изделия первого вида составляет 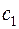 ден.ед, от реализации единицы изделия второго вида –
ден.ед, от реализации единицы изделия второго вида – 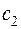 ден.ед.
ден.ед.
|
Тип сырья |
Запас сырья, кг | ||
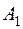
| 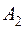
| ||
| 1-й | 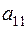
| 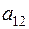
| 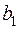
|
| 2-й | 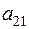
| 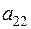
| 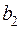
|
| 3-й | 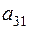
| 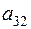
| 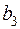
|
| Прибыль, ден.ед. | 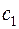
| 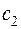
| |
Требуется составить план производства изделий, обеспечивающий максимальную прибыль частного предприятия от реализации продукции, решив задачу геометрическим методом.
Данные к условию задачи, соответствующие вариантам:
1)
|
Тип сырья |
Запас сырья, кг | ||
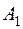
| 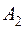
| ||
| 1-й | 4 | 1 | 240 |
| 2-й | 2 | 3 | 180 |
| 3-й | 1 | 5 | 251 |
| Прибыль, ден.ед. | 40 | 30 | |
2)
|
Тип сырья |
Запас сырья, кг | ||
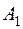
| 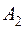
| ||
| 1-й | 1 | 3 | 300 |
| 2-й | 3 | 4 | 477 |
| 3-й | 4 | 1 | 441 |
| Прибыль, ден.ед. | 52 | 39 | |
3)
|
Тип сырья |
Запас сырья, кг | ||
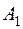
| 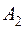
| ||
| 1-й | 3 | 1 | 330 |
| 2-й | 2 | 8 | 800 |
| 3-й | 5 | 6 | 745 |
| Прибыль, ден.ед. | 33 | 24 | |
4)
|
Тип сырья |
Запас сырья, кг | ||
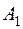
| 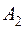
| ||
| 1-й | 5 | 4 | 810 |
| 2-й | 4 | 2 | 630 |
| 3-й | 2 | 6 | 786 |
| Прибыль, ден.ед. | 34 | 36 | |
5)
|
Тип сырья |
Запас сырья, кг | ||
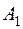
| 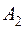
| ||
| 1-й | 5 | 2 | 750 |
| 2-й | 4 | 5 | 807 |
| 3-й | 1 | 7 | 840 |
| Прибыль, ден.ед. | 30 | 49 | |
6)
|
Тип сырья |
Запас сырья, кг | ||
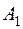
| 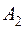
| ||
| 1-й | 2 | 6 | 714 |
| 2-й | 5 | 1 | 600 |
| 3-й | 4 | 3 | 600 |
| Прибыль, ден.ед. | 13 | 21 | |
7)
|
Тип сырья |
Запас сырья, кг | ||
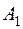
| 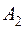
| ||
| 1-й | 1 | 1 | 170 |
| 2-й | 2 | 3 | 438 |
| 3-й | 2 | 1 | 290 |
| Прибыль, ден.ед. | 22 | 15 | |
8)
|
Тип сырья |
Запас сырья, кг | ||
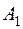
| 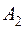
| ||
| 1-й | 5 | 4 | 807 |
| 2-й | 7 | 1 | 840 |
| 3-й | 2 | 5 | 750 |
| Прибыль, ден.ед. | 49 | 30 | |
9)
|
Тип сырья |
Запас сырья, кг | ||
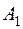
| 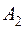
| ||
| 1-й | 4 | 6 | 480 |
| 2-й | 1 | 8 | 445 |
| 3-й | 3 | 2 | 300 |
| Прибыль, ден.ед. | 21 | 56 | |
0)
|
Тип сырья |
Запас сырья, кг | ||
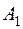
| 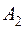
| ||
| 1-й | 2 | 6 | 600 |
| 2-й | 5 | 1 | 401 |
| 3-й | 6 | 4 | 596 |
| Прибыль, ден.ед. | 20 | 11 | |
X . На три базы 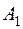 ,
, 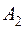 ,
, 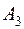 поступил однородный товар соответственно в количестве:
поступил однородный товар соответственно в количестве: 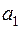 ,
, 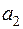 ,
, 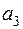 . Товар требуется перевезти в количестве
. Товар требуется перевезти в количестве 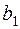 единиц в магазин
единиц в магазин 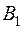 , в количестве
, в количестве 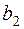 единиц в магазин
единиц в магазин 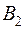 ,
, 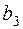 ед. в магазин
ед. в магазин 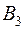 ,
, 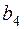 ед. в магазин
ед. в магазин 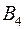 ,
, 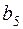 ед. в магазин
ед. в магазин 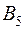 . Матрица тарифов перевозок
. Матрица тарифов перевозок 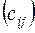 между базами и магазинами, запасы товаров на базах и потребности в товарах для магазинов заданы таблицей:
между базами и магазинами, запасы товаров на базах и потребности в товарах для магазинов заданы таблицей:
| Базы Магазины | 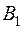
| 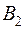
| 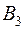
| 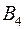
| 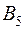
| Запасы 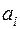
|
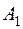
| 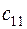
| 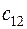
| 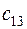
| 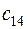
| 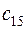
| 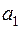
|
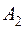
| 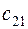
| 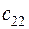
| 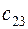
| 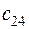
| 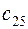
| 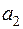
|
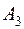
| 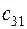
| 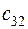
| 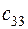
| 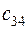
| 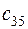
| 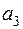
|
Потребности 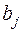
| 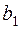
| 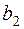
| 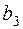
| 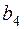
| 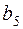
|
Спланировать план перевозок таким образом, чтобы общая их стоимость была минимальной.
Данные к условию задачи, соответствующие вариантам:
1)
| Базы Магазины | 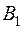
| 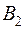
| 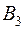
| 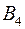
| 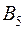
| Запасы 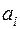
|
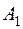
| 14 | 8 | 17 | 5 | 3 | 120 |
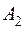
| 21 | 10 | 7 | 11 | 6 | 180 |
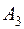
| 3 | 5 | 8 | 4 | 9 | 200 |
Потребности 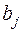
| 70 | 120 | 105 | 125 | 110 |
2)
| Базы Магазины | 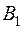
| 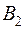
| 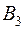
| 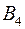
| 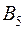
| Запасы 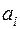
|
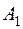
| 21 | 18 | 14 | 3 | 6 | 400 |
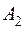
| 7 | 11 | 10 | 5 | 12 | 370 |
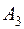
| 4 | 8 | 16 | 9 | 13 | 380 |
Потребности 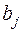
| 250 | 200 | 290 | 260 | 100 |
3)
| Базы Магазины | 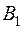
| 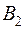
| 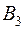
| 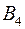
| 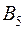
| Запасы 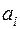
|
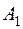
| 14 | 8 | 17 | 5 | 3 | 530 |
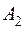
| 21 | 10 | 7 | 11 | 6 | 570 |
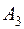
| 3 | 5 | 8 | 4 | 9 | 600 |
Потребности 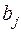
| 300 | 380 | 450 | 370 | 250 |
4)
| Базы Магазины | 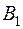
| 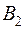
| 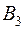
| 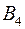
| 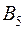
| Запасы 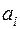
|
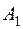
| 2 | 10 | 15 | 14 | 4 | 350 |
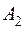
| 3 | 7 | 12 | 5 | 8 | 350 |
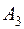
| 21 | 18 | 6 | 13 | 16 | 300 |
Потребности 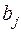
| 180 | 220 | 230 | 270 | 100 |
5)
| Базы Магазины | 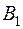
| 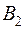
| 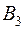
| 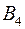
| 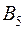
| Запасы 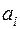
|
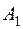
| 12 | 9 | 7 | 11 | 6 | 350 |
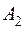
| 4 | 3 | 12 | 2 | 8 | 300 |
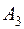
| 5 | 17 | 9 | 4 | 11 | 300 |
Потребности 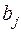
| 180 | 220 | 230 | 270 | 100 |
6)
| Базы Магазины | 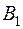
| 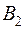
| 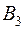
| 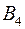
| 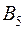
| Запасы 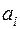
|
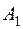
| 2 | 4 | 11 | 5 | 3 | 400 |
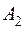
| 8 | 17 | 13 | 7 | 6 | 370 |
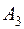
| 14 | 10 | 5 | 8 | 9 | 380 |
Потребности 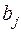
| 250 | 200 | 290 | 210 | 150 |
7)
| Базы Магазины | 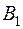
| 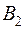
| 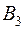
| 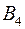
| 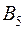
| Запасы 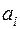
|
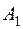
| 2 | 4 | 5 | 11 | 3 | 120 |
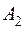
| 12 | 8 | 6 | 14 | 11 | 150 |
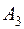
| 10 | 15 | 7 | 9 | 18 | 100 |
Потребности 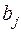
| 85 | 65 | 90 | 60 | 70 |
8)
| Базы Магазины | 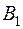
| 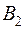
| 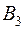
| 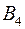
| 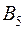
| Запасы 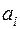
|
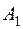
| 3 | 8 | 7 | 11 | 15 | 120 |
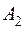
| 14 | 3 | 1 | 8 | 6 | 180 |
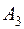
| 9 | 5 | 16 | 7 | 12 | 200 |
Потребности 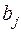
| 70 | 120 | 105 | 125 | 110 |
9)
| Базы Магазины | 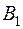
| 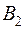
| 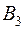
| 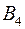
| 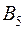
| Запасы 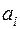
|
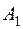
| 11 | 4 | 15 | 7 | 2 | 260 |
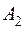
| 20 | 9 | 7 | 14 | 5 | 400 |
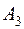
| 18 | 10 | 3 | 8 | 6 | 240 |
Потребности 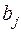
| 180 | 200 | 190 | 230 | 100 |
0)
| Базы Магазины | 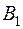
| 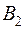
| 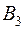
| 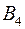
| 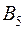
| Запасы 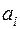
|
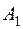
| 12 | 9 | 7 | 11 | 6 | 150 |
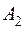
| 4 | 3 | 12 | 2 | 8 | 170 |
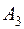
| 5 | 17 | 9 | 4 | 11 | 260 |
Потребности 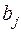
| 100 | 70 | 150 | 150 | 80 |
XI. Даны координаты вершин треугольника АВС. Необходимо
а) написать уравнения сторон треугольника;
б) написать уравнение высоты треугольника проведенной из вершины С к стороне АВ;
в) написать уравнение медианы треугольника, проведенной из вершины В к стороне АС;
г) найти углы треугольника и установить его вид (прямоугольный, остроугольный, тупоугольный);
д) найти длины сторон треугольника и определить его тип (разносторонний, равнобедренный, равносторонний);
К пунктам а) – в) решения сделать рисунки в системе координат. На рисунках обозначить соответствующие пунктам задачи линии и точки.
Данные к условию задачи, соответствующие вариантам:
1) 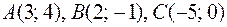 ;
2) ;
2) 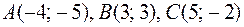 ;
3) ;
3) 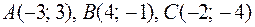 ;
4) ;
4) 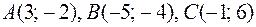 ;
5) ;
5) 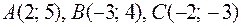 ; ;
| 6) 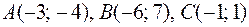 ;
7) ;
7) 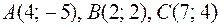 ;
8) ;
8) 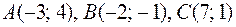 ;
9) ;
9) 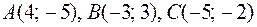 ;
0) ;
0) 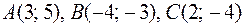 . .
|
II . Выполнив действия над матрицами, найти матрицу К.
Данные к условию задачи, соответствующие вариантам:
1) 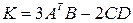 ,
,
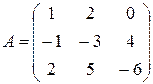 ,
, 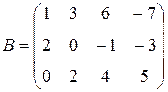 ,
, 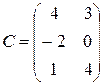 ,
, 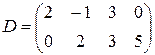 ;
;
2) 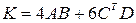 ,
,
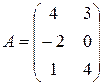 ,
, 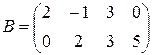 ,
, 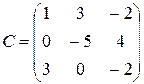 ,
, 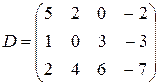 ;
;
3) 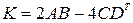 ,
,
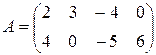 ,
, 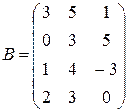 ,
, 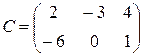 ,
, 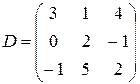 ;
;
4) 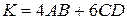 ,
,
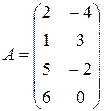 ,
, 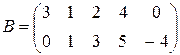 ,
, 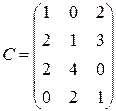 ,
, 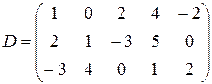 ;
;
5) 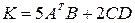 ,
,
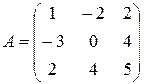 ,
, 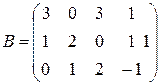 ,
, 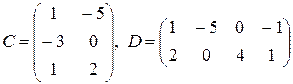 ;
;
6) 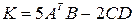 ,
,
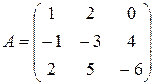 ,
, 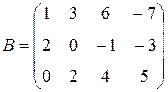 ,
, 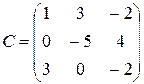 ,
, 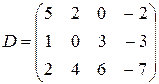 ;
;
7) 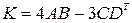 ,
,
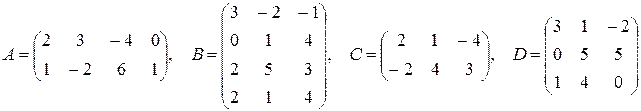 ;
;
8) 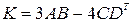 ,
,
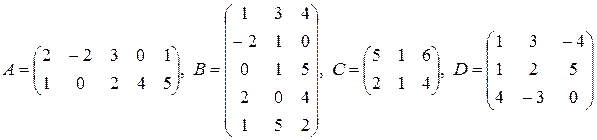 ;
;
9) 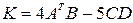 ,
,
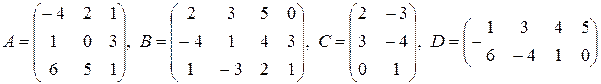 ;
;
0) 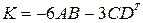 ,
,
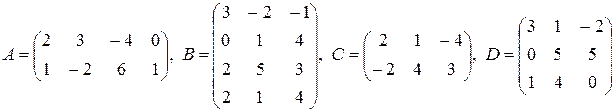 .
.
III . Решить систему:
а) матричным методом (методом обратной матрицы);
б) по формулам Крамера.
Данные к условию задачи, соответствующие вариантам:
1) 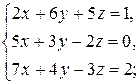
2) 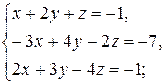
3) 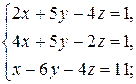
4) 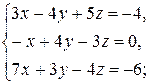
5) 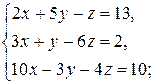
6) 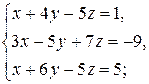
7) 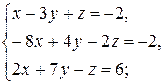
8) 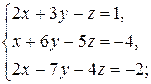
9) 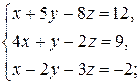
0) 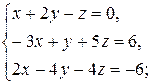
Дата: 2018-12-21, просмотров: 487.