1o. Интегралы вида
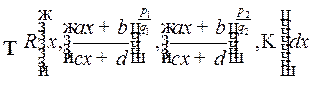, (1)
где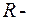 
рациональная функция и 
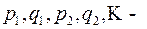целые числа.
Интегралы вида (1) находятся с помощью подстановки
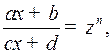
где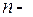 
наименьшее общее кратное чисел 
.
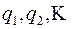Пример 1. Найти
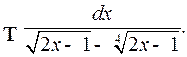
Решение. Подстановка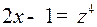 
приводит интеграл к виду
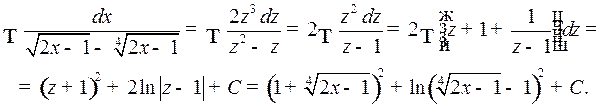
Пример 2. Найти интеграл
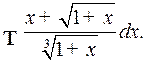
Решение. Наименьшее общее кратное показателей корней в подынтегральном выражении равно 6, поэтому делаем подстановку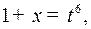 
откуда 
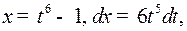то есть
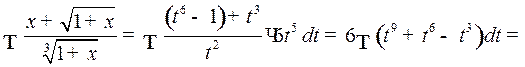
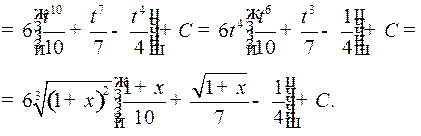
Пример 3. Найти интеграл
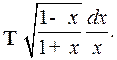
Решение. Сделаем подстановку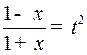 
.
Отсюда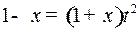 
т.е.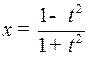 
,
и значит,
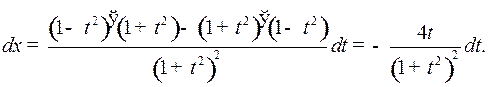
Таким образом,
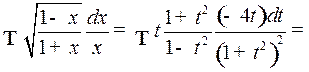
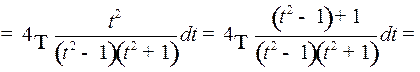
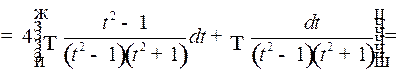
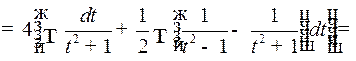
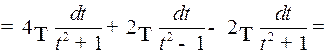
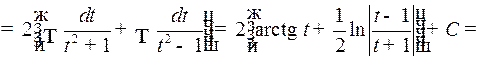
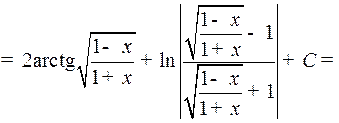
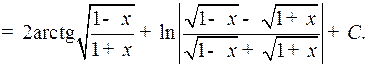
2o. Интегралы вида
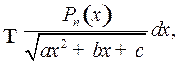
где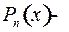 
многочлен степени 
.
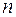Полагают,
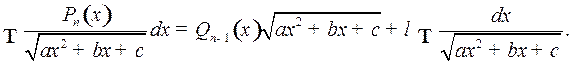(3)
где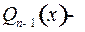 
многочлен степени 
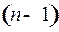с неопределенными коэффициентами и 
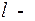число.
Коэффициенты многочлена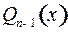 
и число 
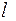находятся при помощи дифференцирования тождества (3).
Пример 4.
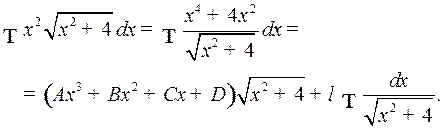
Отсюда
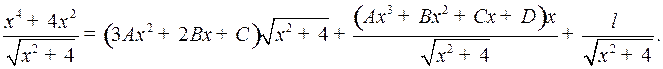
Умножая на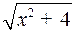 
и приравнивая коэффициенты при одинаковых степенях 
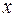, получим:
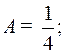
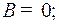
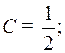
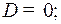
Следовательно,
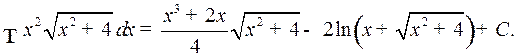
3o . Интегралы вида
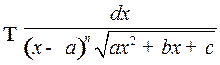(4)
приводится к интегралам вида (2) с помощью подстановки
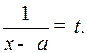
4o . Интегралы от дифференциальных биномов
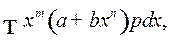(5)
где 
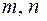и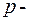 
рациональные числа.
Условия Чебышева. Интеграл (5) выражается через конечную комбинацию элементарных функций лишь в следующих трех случаях:
1) если 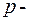целое число;
2) если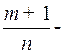 
целое число. Здесь применяется подстановка 
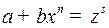, где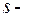 
знаменатель дроби 
;
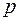3) если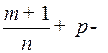 
целое число. В этом случае используется подстановка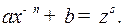 
Пример 3. Найти
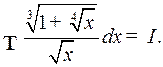
Решение. Здесь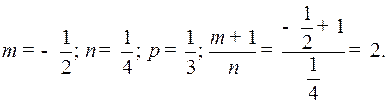 
Следовательно, имеет место случай 2) интегрируемости.
Подстановка
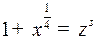
дает: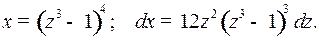 
Поэтому
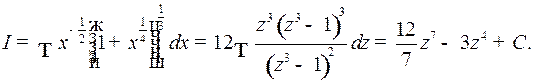
где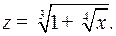 
Интегрирование тригонометрических функций
1o. Интегралы вида
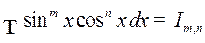(1)
где 
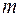и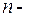 
целые числа.
1) Если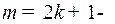 
нечетное положительное число, то полагают
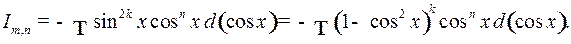
Аналогично поступают, если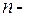 
нечетное положительное число.
Пример 1.
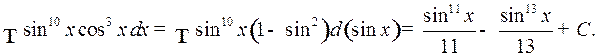
2) Есл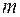и 
и 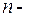четные положительные числа, то подынтегральное выражение (1) преобразуют с помощью формул:
.
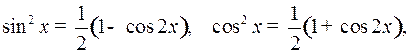
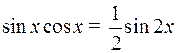Пример 2.
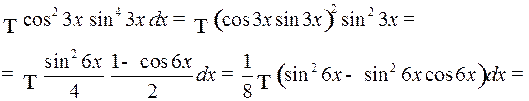
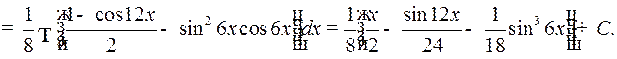
3) Есл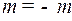и 
и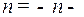 
целые отрицательные числа одинаковой четности, то
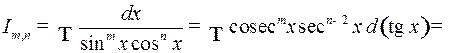
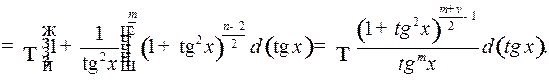
В частности, к этому случаю сводятся интегралы
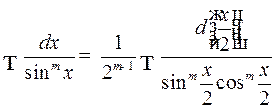и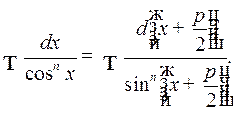 
Пример 3.
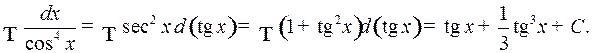
Пример 4.
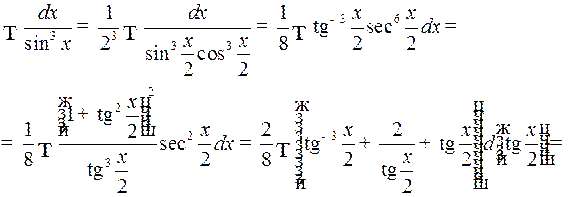
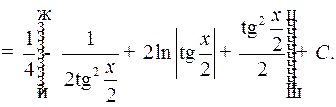
4) Интегралы вида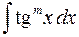 
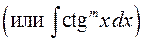, где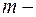 
целое положительное число, вычисляются с помощью формулы
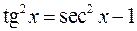
(или соответственно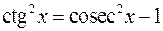 
).
Пример 5.
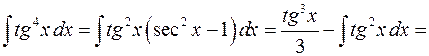
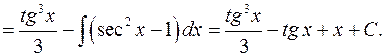
5) В общем случае интегралы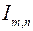 
вида (1) вычисляются с помощью формул приведения (рекуррентных формул), выводимых обычно интегрированием по частям.
Пример 6.
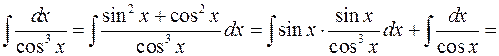
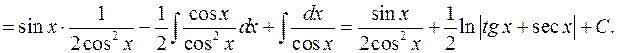
2o. Интегралы вида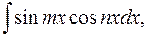 
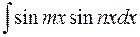и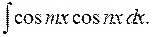 
В этих случаях применяются формулы:
1) 
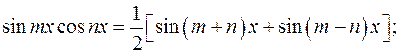
2) 
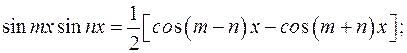
3) 
.
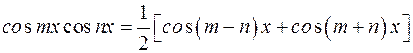Пример 7.
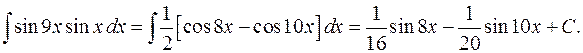
3o. Интегралы вида
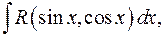(2)
где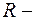 
рациональная функция.
1) С помощью подстановки
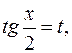
откуда
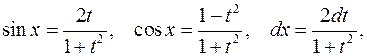
интегралы вида (2) приводятся к интегралам от рациональных функций новой переменной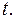 
Пример 8. Найти
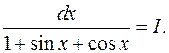
Решение. Полагая 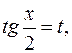будем иметь:
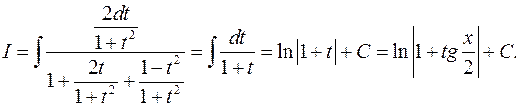
2) Если имеет место тождество
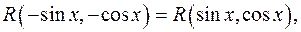
то для приведения интеграла (2) к рациональному виду можно применить подставку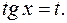 
Здесь
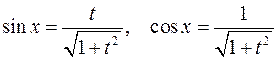
и
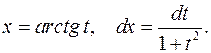
Пример 9. Найти
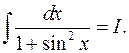(3)
Решение. Полагая
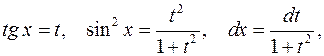
будем иметь:
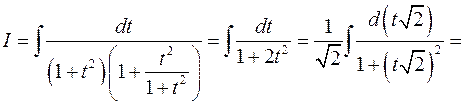
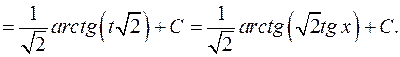
Заметим, что интеграл (3) вычисляется более быстро, если предварительно числитель и знаменатель дроби разделить на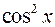 
.
Дата: 2018-12-21, просмотров: 552.
