ВВЕДЕНИЕ
Настоящие методические указания предназначены для студентов всех специальностей и направлений бакалаврской подготовки заочной формы обучения, выполняющих расчетно-графическую работу по интегральному исчислению. Методические указания состоят из трех частей. В первой главе рассматриваются основные классы интегрируемых в конечном виде функций. Во второй главе рассматриваются определенные интегралы и их приложения. Третья глава содержит варианты расчетной работы. Приведены краткие теоретические сведения типовые задачи и примеры, позволяющие успешно справиться с аналогичными заданиями самостоятельно.
ГЛАВА I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Неопределенное интегрирование
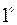. Основные правила интегрирования.
1) Если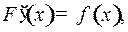 
то
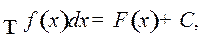
где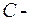 
произвольная постоянная.
2) 
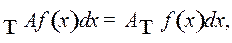где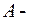 
постоянная величина.
3) 
4) Если 
и 
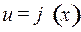, то
.
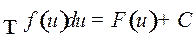В частности,
.
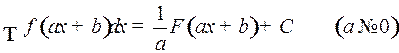. Таблица простейших интегралов.
1. 
, 
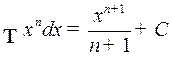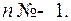
2. 
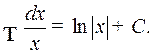
3. 
, 
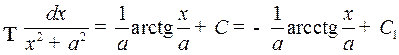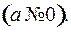
4. 
,
,
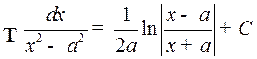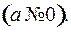
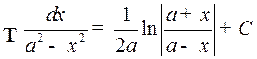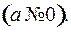
5. 
,
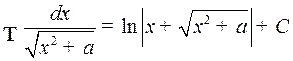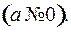
6. 
, 
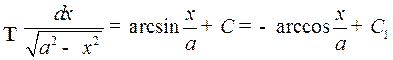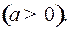
7. 
, 
.
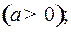
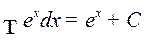8. 
.
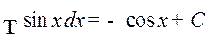9. 
.
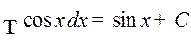10. 
.
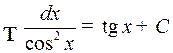11. 
.
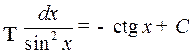12. 
.
13. 
.
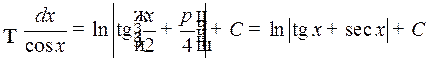14. 
.
15. 
.
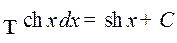16. 
.
17. 
.
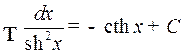Пример 1.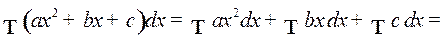 
.
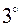. Интегрирование путем подведения под знак дифференциала.
Правило 4) значительно расширяет таблицу простейших интегралов. А именно, в силу этого правила таблица интегралов оказывается справедливой независимо то того, является переменная интегрирования независимой переменной или дифференцируемой функцией.
Пример 2.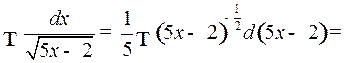 
,
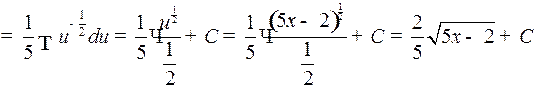где было положено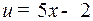 
. Использовалось правило 4) и табличный интеграл 1.
Пример 3.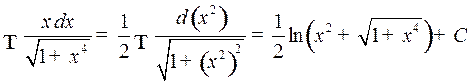 
.
Неявно подразумевалось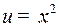 
, причем применялось правило 4) и табличный интеграл 5.
Пример 4.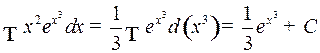 
в силу правила 4) и табличного интеграла 7.
В примерах 2, 3, 4, прежде чем использовать тот или иной табличный интеграл, мы приводили данный интеграл к виду
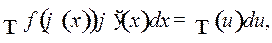где .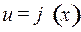
Такого рода преобразование называется подведением под знак дифференциала.
Полезно отметить часто применяемые преобразования дифференциалов, которые, в частности, использовались в примерах 2 и 3:
а)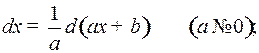 
б)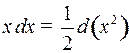 
и т.п.
Метод подстановки
1o. Замена переменной в неопределенном интеграле.
Полагая
,
где 
новая переменная и 
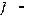непрерывно дифференцируемая функция, будем иметь:
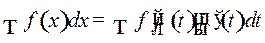. (1)
Функцию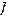 
стараются выбирать таким образом, чтобы правая часть формулы (1) приобрела удобный для интегрирования вид.
Пример 1. Найти
.
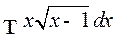Решение. Естественно положить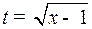 
, отсюда 
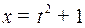, и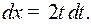 
Следовательно,
.
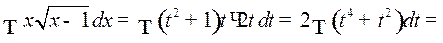
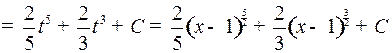Иногда применяются подстановки вида
Допустим, что нам удалось подынтегральное выражение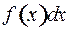 
преобразовать к такому виду:
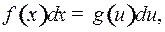где
Если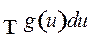 
известен, т.е.
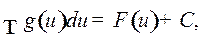
то
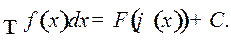
Этим способом мы уже, собственно говоря, пользовались в § 1. 
.
Примеры 2, 3, 4 (§ 1) можно было решить следующим образом
Пример 2.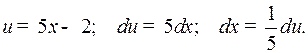 
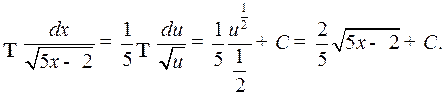
Пример 3.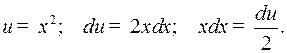 
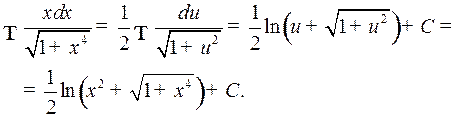
Пример 4.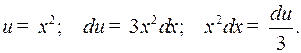 
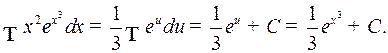
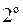. Тригонометрические подставки. Пусть 
тогда:
1) Если интеграл содержит радикал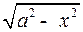 
, то обычно полагают 
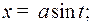отсюда
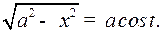
2) Если интеграл содержит радикал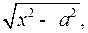 
то полагают 
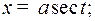отсюда
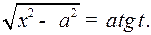
3) Если интеграл содержит радикал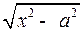 
, то полагают 
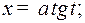отсюда
Заметим, что тригонометрические подстановки не всегда оказываются выгодными.
Иногда вместо тригонометрических подстановок удобнее пользоваться гиперболическими подстановками, которые имеют аналогичный характер.
Пример 5. Найти
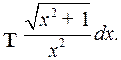
Решение. Полагаем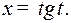 
Следовательно,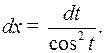 
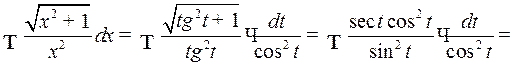
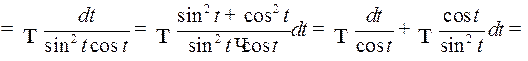
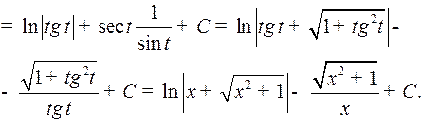
Пример 6. Найти
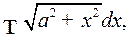
применяя гиперболическую подстановку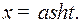 
Решение. Имеем 
и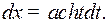 
Отсюда
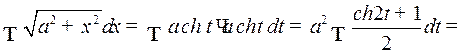
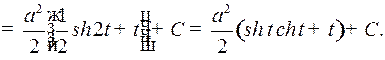
Так как
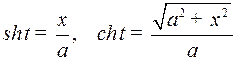
и
то окончательно получаем:
где 
новая произвольная постоянная.
Интегрирование по частям
Метод интегрирования по частям основан на формуле:
,
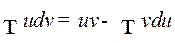где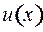 
и 
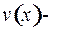непрерывно дифференцируемые функции.
Эту формулу иногда записывают в эквивалентной форме:
.
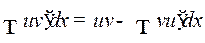Если внимательно посмотреть на эти формулы, то можно заметить, что исходный интеграл 
выразился через интеграл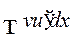 
, в котором производная «перебросилась» с одного сомножителя на другой. В ряде случаев интеграл при этом получается проще. В этом весь смысл метода интегрирования по частям. Не следует думать, что этот прием будет хорошо работать всегда – применение формулы интегрирования по частям не к месту может сделать исходный интеграл еще сложнее. Но есть по крайней мере два стандартных случая, в которых этот метод всегда приводит к цели:
1. Интеграл вида
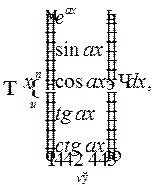где 
2. Интеграл вида
.
В общих случаях одним из сомножителей является целая степень переменной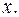 
Вторым сомножителем в первом случае является показательная или одна из тригонометрических функций, а во втором случае – одна из обратных.
При использовании формулы интегрирования по частям нужно определиться, какой из сомножителей взять в качестве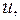 
а в какой в качестве 
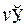В случае 1 производную надо перебрасывать на 
. При этом в интеграле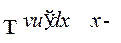 
степень станет не единицу меньше. Применяя формулу интегрирования по частям 
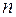раз, можно избавиться от сомножителя 
.
В случае 2 нужно, наоборот, производную перебросить на второй сомножитель.
Пример 1. Найти интеграл
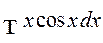
Полагаем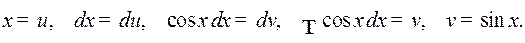 
Тогда
Пример 2. Найти интеграл
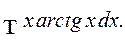
Это интеграл вида 2. Полагаем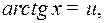 
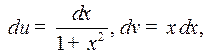
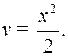
Тогда получим
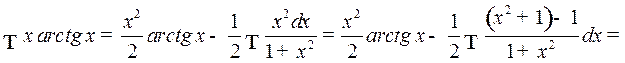
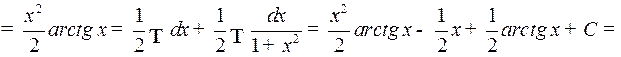
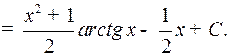
Заметим, что для использования формулы интегрирования по частям нам необходимо по функции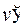 
найти функцию 
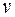, т.е. проинтегрировать 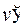. Поэтому в качестве 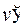нужно брать по крайней мере легко интегрируемую функцию.
Есть еще один стандартный тип интегралов, применение к которым формулы интегрирования по частям приводит к цели. Это интегралы вида
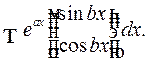
Пример 3. Найти
Решение. Имеем:
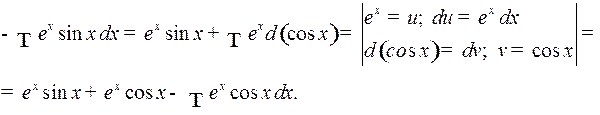
Следовательно,
откуда
Пример 3.
.
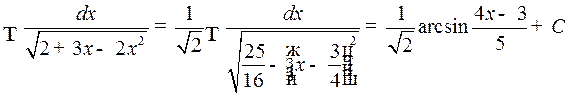Пример 4.
.
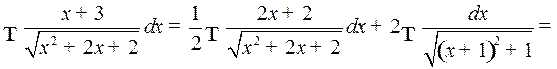
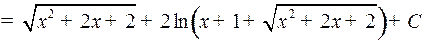. Интегралы вида 
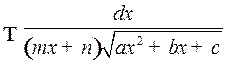. С помощью обратной подстановки
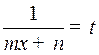
эти интегралы приводятся к интегралам вида 
.
Пример 5. Найти
.
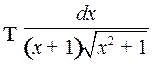Решение. Полагаем
,
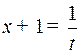отсюда
.
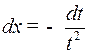Имеем: 
.
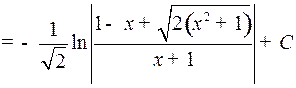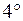. Интегралы вида 
. Путем выделения из квадратного трехчлена полного квадрата данный интеграл сводится к одному из следующих основных интегралов:
1) 
,
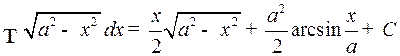2) 
.
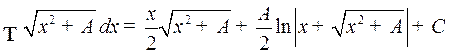Пример 6.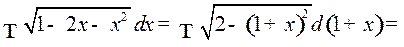 
.
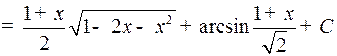Пример 1.
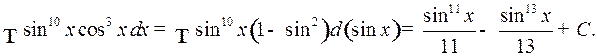
2) Если 
и 
четные положительные числа, то подынтегральное выражение (1) преобразуют с помощью формул:
.
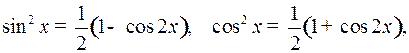
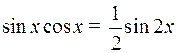Пример 2.
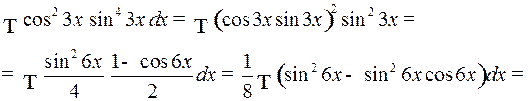
3) Есл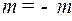и 
и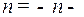 
целые отрицательные числа одинаковой четности, то
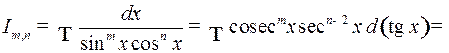
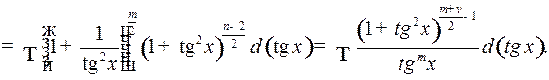
В частности, к этому случаю сводятся интегралы
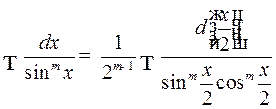и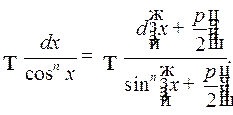 
Пример 3.
Пример 4.
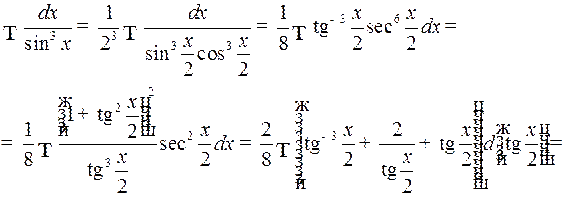
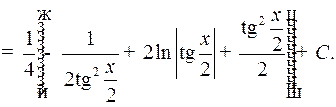
4) Интегралы вида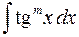 
, где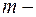 
целое положительное число, вычисляются с помощью формулы
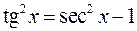
(или соответственно 
).
Пример 5.
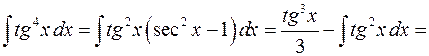
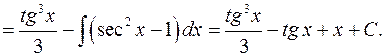
5) В общем случае интегралы 
вида (1) вычисляются с помощью формул приведения (рекуррентных формул), выводимых обычно интегрированием по частям.
Пример 6.
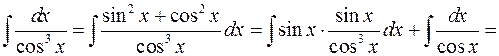
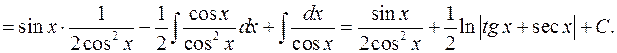
2o. Интегралы вида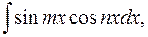 
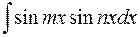и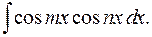 
В этих случаях применяются формулы:
1) 
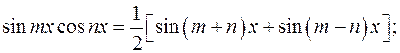
2) 
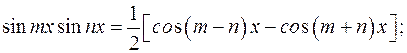
3) 
.
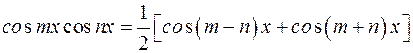Пример 7.
3o. Интегралы вида
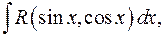(2)
где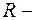 
рациональная функция.
1) С помощью подстановки
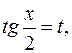
откуда
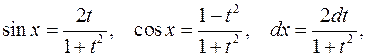
интегралы вида (2) приводятся к интегралам от рациональных функций новой переменной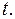 
Пример 8. Найти
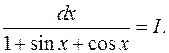
Решение. Полагая 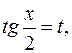будем иметь:
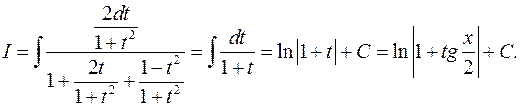
2) Если имеет место тождество
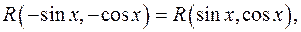
то для приведения интеграла (2) к рациональному виду можно применить подставку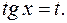 
Здесь
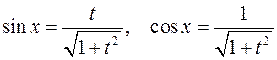
и
Пример 9. Найти
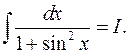(3)
Решение. Полагая
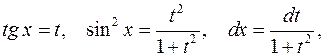
будем иметь:
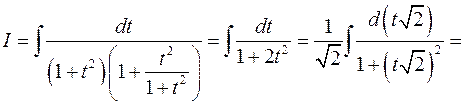
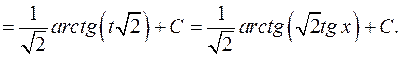
Заметим, что интеграл (3) вычисляется более быстро, если предварительно числитель и знаменатель дроби разделить на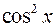 
.
ВВЕДЕНИЕ
Настоящие методические указания предназначены для студентов всех специальностей и направлений бакалаврской подготовки заочной формы обучения, выполняющих расчетно-графическую работу по интегральному исчислению. Методические указания состоят из трех частей. В первой главе рассматриваются основные классы интегрируемых в конечном виде функций. Во второй главе рассматриваются определенные интегралы и их приложения. Третья глава содержит варианты расчетной работы. Приведены краткие теоретические сведения типовые задачи и примеры, позволяющие успешно справиться с аналогичными заданиями самостоятельно.
ГЛАВА I
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Неопределенное интегрирование
. Основные правила интегрирования.
1) Если 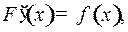то
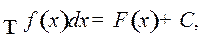
где 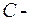произвольная постоянная.
2) 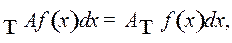где 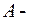постоянная величина.
3)
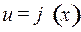4) Если и , то
.
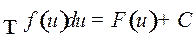В частности,
.
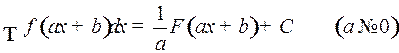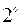. Таблица простейших интегралов.
1. ,
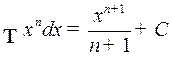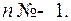
2.
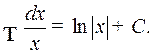
3. ,
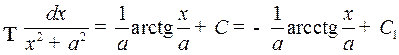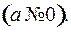
4. ,
,
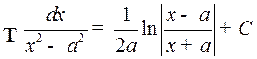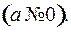
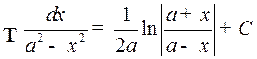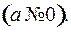
5. ,
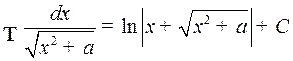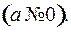
6. ,
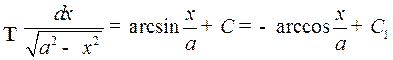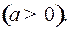
7. , .
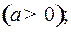
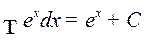8. .
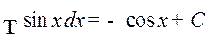9. .
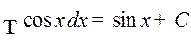10. .
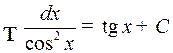11. .
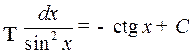12. .
13. .
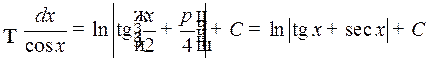14. .
15. .
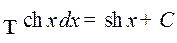16. .
17. .
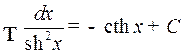Пример 1.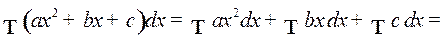
.
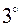. Интегрирование путем подведения под знак дифференциала.
Правило 4) значительно расширяет таблицу простейших интегралов. А именно, в силу этого правила таблица интегралов оказывается справедливой независимо то того, является переменная интегрирования независимой переменной или дифференцируемой функцией.
Пример 2.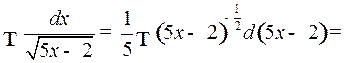
,
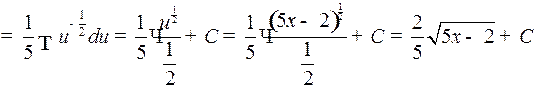где было положено 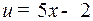. Использовалось правило 4) и табличный интеграл 1.
Пример 3. .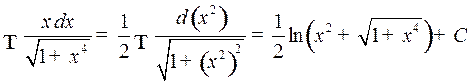
Неявно подразумевалось 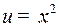, причем применялось правило 4) и табличный интеграл 5.
Пример 4. 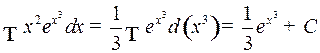в силу правила 4) и табличного интеграла 7.
В примерах 2, 3, 4, прежде чем использовать тот или иной табличный интеграл, мы приводили данный интеграл к виду
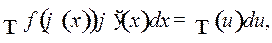где .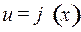
Такого рода преобразование называется подведением под знак дифференциала.
Полезно отметить часто применяемые преобразования дифференциалов, которые, в частности, использовались в примерах 2 и 3:
а)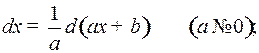
б) 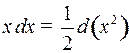и т.п.
Метод подстановки
1o. Замена переменной в неопределенном интеграле.
Полагая
,
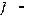где новая переменная и непрерывно дифференцируемая функция, будем иметь:
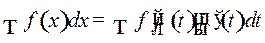. (1)
Функцию 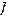стараются выбирать таким образом, чтобы правая часть формулы (1) приобрела удобный для интегрирования вид.
Пример 1. Найти
.
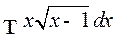Решение. Естественно положить 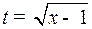, отсюда 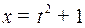, и 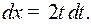Следовательно,
.
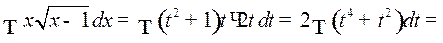
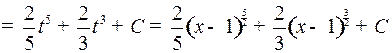Иногда применяются подстановки вида
Допустим, что нам удалось подынтегральное выражение 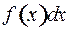преобразовать к такому виду:
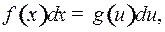где
Если 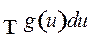известен, т.е.
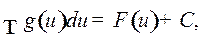
то
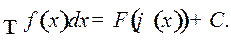
Этим способом мы уже, собственно говоря, пользовались в § 1. .
Примеры 2, 3, 4 (§ 1) можно было решить следующим образом
Пример 2.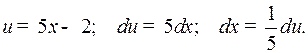
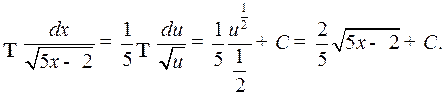
Пример 3.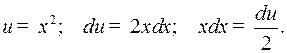
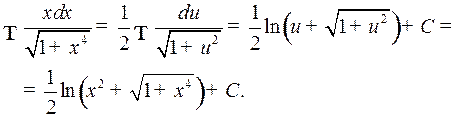
Пример 4.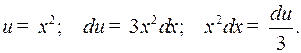
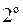. Тригонометрические подставки. Пусть тогда:
1) Если интеграл содержит радикал 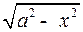, то обычно полагают 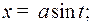отсюда
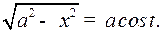
2) Если интеграл содержит радикал 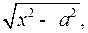то полагают 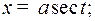отсюда
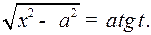
3) Если интеграл содержит радикал 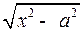, то полагают 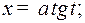отсюда
Заметим, что тригонометрические подстановки не всегда оказываются выгодными.
Иногда вместо тригонометрических подстановок удобнее пользоваться гиперболическими подстановками, которые имеют аналогичный характер.
Пример 5. Найти
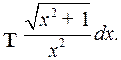
Решение. Полагаем 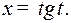Следовательно,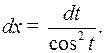
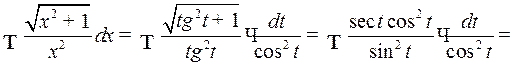
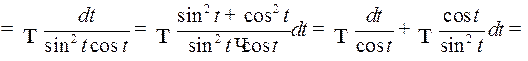
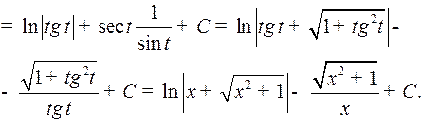
Пример 6. Найти
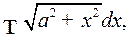
применяя гиперболическую подстановку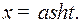
Решение. Имеем и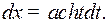
Отсюда
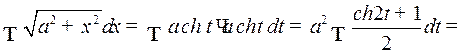
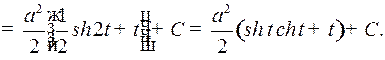
Так как
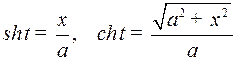
и
то окончательно получаем:
где новая произвольная постоянная.
Интегрирование по частям
Метод интегрирования по частям основан на формуле:
,
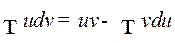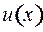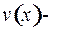где и непрерывно дифференцируемые функции.
Эту формулу иногда записывают в эквивалентной форме:
.
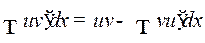Если внимательно посмотреть на эти формулы, то можно заметить, что исходный интеграл выразился через интеграл 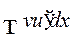, в котором производная «перебросилась» с одного сомножителя на другой. В ряде случаев интеграл при этом получается проще. В этом весь смысл метода интегрирования по частям. Не следует думать, что этот прием будет хорошо работать всегда – применение формулы интегрирования по частям не к месту может сделать исходный интеграл еще сложнее. Но есть по крайней мере два стандартных случая, в которых этот метод всегда приводит к цели:
1. Интеграл вида
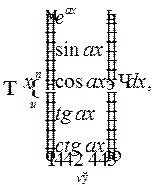где
2. Интеграл вида
.
В общих случаях одним из сомножителей является целая степень переменной 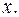Вторым сомножителем в первом случае является показательная или одна из тригонометрических функций, а во втором случае – одна из обратных.
При использовании формулы интегрирования по частям нужно определиться, какой из сомножителей взять в качестве 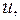а в какой в качестве 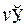В случае 1 производную надо перебрасывать на . При этом в интеграле 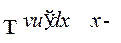степень станет не единицу меньше. Применяя формулу интегрирования по частям 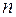раз, можно избавиться от сомножителя .
В случае 2 нужно, наоборот, производную перебросить на второй сомножитель.
Пример 1. Найти интеграл
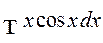
Полагаем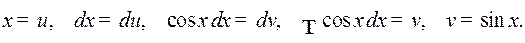
Тогда
Пример 2. Найти интеграл
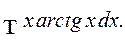
Это интеграл вида 2. Полагаем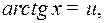
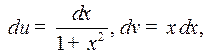
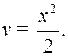
Тогда получим
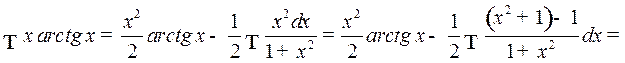
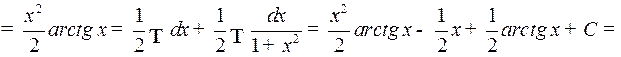
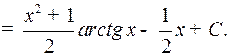
Заметим, что для использования формулы интегрирования по частям нам необходимо по функции 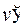найти функцию 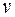, т.е. проинтегрировать 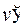. Поэтому в качестве 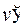нужно брать по крайней мере легко интегрируемую функцию.
Есть еще один стандартный тип интегралов, применение к которым формулы интегрирования по частям приводит к цели. Это интегралы вида
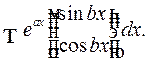
Пример 3. Найти
Решение. Имеем:
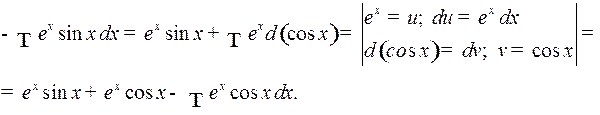
Следовательно,
откуда
Дата: 2018-12-21, просмотров: 367.
