В.Г.Николаев,
ведущий научный сотрудник Учреждения Российской академии наук Института химии и технологии редких элементов и минерального сырья
им. И.В. Тананаева Кольского научного центра РАН,
доктор технических наук, старший научный сотрудник
А.Е. Иванов,
доцент кафедры химических технологий и строительного материаловедения
Апатитского филиала Мурманского государственного технического университета, кандидат химических наук, доцент
Шейко Е.М., Енбаева Е.С.
Электроника. Часть II: Цифровая электроника: учеб. пособие. – Апатиты: Изд. Кольского филиала ПетрГУ, 2010. – 103 с.
Учебное пособие содержит курс лекций по дисциплине «Электроника», читаемый студентам Кольского филиала Петрозаводского государственного университета. В части II пособия изложены основы цифровой электроники, основные понятия об устройствах на ее основе. В доступной форме излагаются физические основы работы и технические показатели наиболее типичных и распространенных электронных приборов, а также принципы построения простейших электронных схем.
Издание подготовлено в соответствии с государственными образовательными стандартами и предназначено для студентов очной и заочной форм обучения техническим специальностям: 140402 «Теплофизика», 210301 «Радиофизика и электроника», 140201 «Высоковольтные электроэнергетика и электротехника», 140604 «Электропривод и автоматика промышленных установок и технологических комплексов», 130401 «Физические процессы (горного или нефтегазового) производств, 130403 «Открытые горные работы», 130404 «Подземная разработка месторождений полезных ископаемых», 130405 «Обогащение полезных ископаемых», 020302 «Геофизика». Учебное пособие может быть полезно аспирантам и инженерам.
Табл.− 6, ил. − 69, библиогр. − 15 назв.
УДК 622:620.2
ББК 30.3
Е.М. Войтышина, Е.С. Енбаева, 2010
Кольский филиал Петрозаводского
государственного университета, 2010
• Алгебра логики.
В устройствах цифровой электроник используются элементы входные выходные сигналы которых могут принимать лишь 2 значения: логический нуль и логическая единица. Для описания алгоритмов работы и структуры логических схем используют алгебру логики. Алгебра логики также называется булевой алгеброй. В алгебре логики определены отношение эквивалентности (=) и три операции : логическое отрицание (НЕ); логическое сложение (ИЛИ); логическое умножение (И).
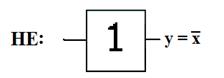
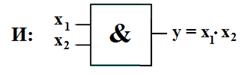
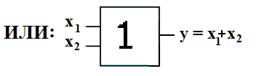
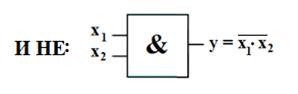
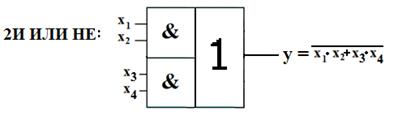
Рис. Условное обозначение основных логических операций.
В булевой алгебре широко применяются таблицы истинности. Таблица истинности – это таблица, содержащая все возможные комбинации значений входных переменных и соответствующие им значение функции. Она состоит из n переменных; 2n строк; n+1 столбцов.
Приведём таблицы истинности основных логических операций.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим пример:
.
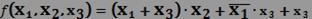
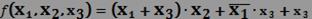| x1 | x2 | x3 | x1+x3 |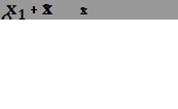 
| 
| 
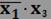
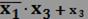
| y |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
• Преобразователи кодов.
Семисегментный индикатор.
Операция изменения кода числа называется его перекодированием. Интегральные микросхемы, выполняющие эти операции, называются преобразователями кодов.
Преобразователи кодов бывают простые и сложные. К простым относятся преобразователи, которые выполняют стандартные операции изменения кода чисел, например, преобразований двоичного кода в одинарный или обратную операцию. Сложные преобразователи кодов выполняют нестандартные преобразования кодов и их схемы приходится разрабатывать каждый раз с помощью алгебры логики.
Будем считать, что преобразователи кодов имеют п входов и к выходов. Соотношения между п и к могут быть любыми: п=к, п<к и п>к. При преобразовании кода чисел с ними могут выполняться различные дополнительные операции, например, умножение на весовые коэффициенты. Примером невесового преобразования является преобразование двоично-десятичного кода в двоичный. Весовые преобразователи кодов используются при преобразовании числовой информации.
В качестве примера рассмотрим преобразователь двоичного кода в код управления семисегментным цифровым индикатором. Сам индикатор представляет собой полупроводниковый прибор, в котором имеются семь сегментов, выполненных из светодиодов. Включением и выключением отдельных сегментов можно получить светящееся изображение отдельных цифр или знаков.
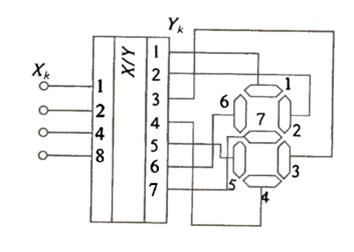
Рис.1 Схема семисегментного индикатора.
Каждой цифре соответствует свой набор включения определенных сегментов индикатора. В таблице также приведены двоичные коды соответствующих цифр. Такие индикаторы позволяют получить светящееся изображение не только цифр от 0 до 9, но других знаков, используемых в 8- и 16-ричной системах счисления.
| n | Сегменты Yk | Код Xk | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 4 | 2 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 3 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 6 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
Таблица соответствия кодов семисегментного индикатора.
Шкальные индикаторы представляют собой линейку светодиодов с одним общим анодом или катодом. Преобразователи двоичного кода в код управления шкальным индикатором обеспечивают перемещение светящегося пятна, определяемое двоичным кодом на адресном входе.
Матричные индикаторы представляют собой наборы светодиодов, расположенных по строкам и столбцам. Наиболее распространенными матричними индикаторами являются индикаторы, имеющие 5 столбцов и 7 строк (формат 5x7). Количество светодиодов в таких матричных индикаторах равно 35. Управление такими индикаторами производится путем выбора номера строки и номера столбца, на пересечении которых находится нужный светодиод.
Для управления матричными индикаторами выпускаются микросхемы, в которых положение светодиода задается номерами столбца i и строки j, причем не все комбинации i и j используются. Такие преобразователи кодов называются неполными.
Примерами простейших преобразователей кодов, которые широко применяются в цифровых устройствах, являются шифраторы и дешифраторы.
Шифратор и Дешифратор.
Шифратором называют кодовый преобразователь, который имеет п входов и k выходов, и при подаче сигнала на один из входов (обязательно только на один) на выходах появляется двоичный код возбужденного входа. Очевидно, что число выходов и входов в полном шифраторе связано соотношением n=2k.
Рассмотрим принцип построения шифратора на примере преобразования 8-разрядного единичного кода в двоичный код. Приведём схему шифратора и его условное схематичное обозначение.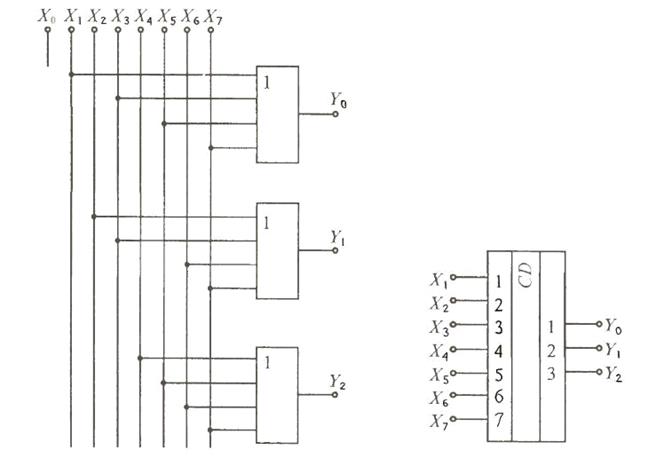 
Рис.1 Схема шифратора и его схематичное обозначение.
Если все входные сигналы имеют нулевое значение, то на выходе шифратора будем иметь нулевой код YQ=Yl = Y2=0. Младший вход с весовым коэффициентом, равным 1, должен возбуждаться при входном сигнале на любом из нечётных входов(1,3,5,7), так как все нечетные номера в двоичном представлении содержат единицу в младшем разряде.
Следующий выход имеет весовой коэффициент два. Он должен возбуждаться при подаче сигналов на входы с номерами 2, 3, 6, 7, т. е. с номерами, имеющими в двоичном представлении единицу во втором разряде.
Старший разряд двоичного кода формируется из входных сигналов с номерами 4, 5, 6 и 7, т. е. из четырех старших разрядов единичного кода. Все рассмотренные состояния шифратора приведем в таблицу.
| X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | Y2 | Y1 | Y0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
Таблица состояний шифратора.
Как следует из выполненного построения, при помощи шифратора можно сократить (сжать) информацию для передачи ее по меньшему числу линий связи, так как к<п. Очевидно, что максимальное число входов шифратора не может превышать количество возможных комбинаций выходных сигналов, т. е. необходимо выполнение условия n ≤ 2k.
В цифровых системах с помощью шифраторов обеспечивается связь между различными устройствами посредством ограниченного числа линий связи. Так, например, в кнопочных пультах управления ввод числовых данных обычно выполняется в унитарном коде посредством нажатия одной из десяти кнопок, а ввод данных в микропроцессор выполняется в двоичном коде. Для такого преобразования используют шифратор из «10 в 4» Поскольку 4х разрядный шифратор имеет не 10 а 16 возможных комбинаций, то такой шифратор является не полным.
Обратное преобразование, т. е. восстановление информации в первоначальном виде можно выполнить с помощью прибора который называется дешифратор.
Дешифратором называют преобразователь двоичного n-разрядного кода в унитарный 2n-разрядный код, все разряды которого, за исключением одного, равны нулю. Дешифраторы бывают полные и неполные. Для полного дешифратора выполняется условие:
N=2n, (15.2)
где n — число входов, а N — число выходов.
В неполных дешифраторах имеется n входов, но реализуется N<2n выходов, так, например, дешифратор, имеющий 4 входа и 10 выходов будет неполным, а дешифратор, имеющий 2 входа и 4 выхода, будет полным.
Рассмотрим принцип построении дешифратора на примере преобразования разрядного двоичного кода в унитарный код. Для полного дешифратора можно записать восемь упорядоченных уравнений:
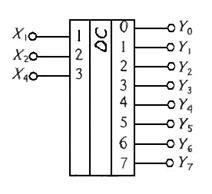
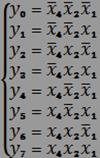
Рис.2 Система уравнений дешифратора его схематичное обозначение;
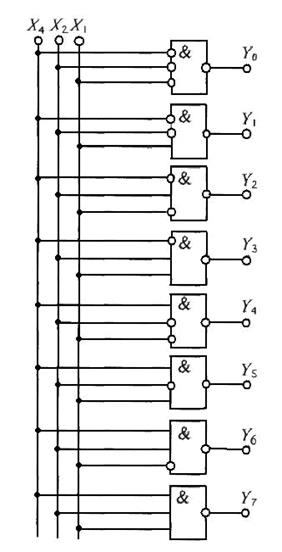
Рис.3 Схема дешифратора.
Сумматор.
Сумматор является комбинационным устройством, предназначенным для сложения чисел.
Комбинационные устройства – устройства, на выходах которого в некоторый момент времени однозначно определяются входными сигналами в этот же момент.
Для сложения 2х одноразрядных чисел А и В необходимо реализовать устройство которое называется полусумматором. Приведём логическую схему и таблицу истинности полусумматора. Отметим, что относительно столбца S реализуется логическая функция “исключающего ИЛИ ”.
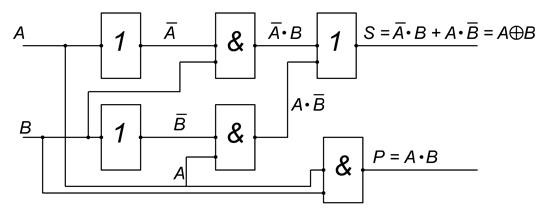
Рис.1 Логическая схема полусумматора
| A | B | S | P |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Таблица истинности полусумматора
Поскольку полусумматор имеет только 2 выхода, то он может использоваться для суммирования лишь в младшем порядке. При суммировании 2х многоразрядных чисел каждого разряда кроме младшего необходимо использовать устройство имеющее дополнительно вход переноса Pвх. Такое устройство называют полным сумматором и его можно представить, как объединение двух полусумматоров логической операцией ИЛИ. Соединяя особым образом полусумматоры и сумматоры можно получить устройство для сложения многоразрядных чисел.
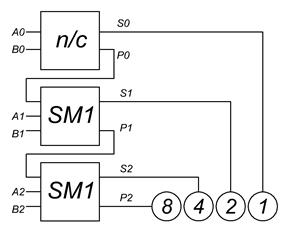
Рис.2 Параллельный сумматор.
При вычитании чисел необходимо проделать ряд дополнительных операций. Сначала вычитаемое число записываем в обратном коде, причём уменьшаемое число остаётся прежним а операция «–» заменяется на «+».
Апр – Впр = Апр + Вобр.
• Если А>В т.е. ответ положительное число, то при формируется единица в старшем разряде а к результату суммы необходимо добавить единицу к младшему разряду.
Апр – Впр = Апр + Вобр = Sпр
• Если А<В т.е. ответ отрицательный то 1 единица в старшем разряде не формируется, а результат суммы при этом представлен в обратном коде.
Апр – Впр = Апр + Вобр = Sобр
Цифровые компараторы.
Цифровые компараторы выполняют сравнение 2х чисел заданных в двоичном коде. Они могут определять равенство двоичных чисел А и В с одинаковым количеством разрядов, либо в виде неравенства.
Компараторы имеют три выхода. На рисунке представлена схема одноразрядного компаратора, представляющая собой структуру логического элемента.
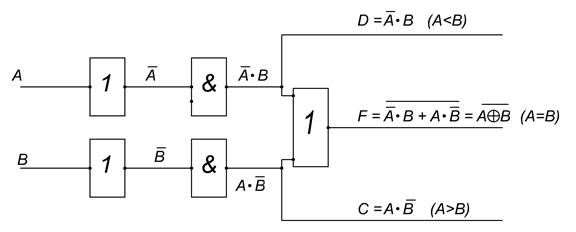
Рис.3 Логическая схема компаратора.
Сравнение чисел происходит попарно, начиная со старшего разряда. В случае неравенства старших разрядов будут задействованы выходы либо D либо С, в случае равенства старших разрядов сравнение переходит в следующий разряд, и так до младшего, при условии равенства всех остальных. В случае если 2 числа равны будет задействован выход F.
Компараторы выполняются как самостоятельные микросхемы, чаще всего 4х разрядные, а для наращивания разрядов сравниваемых чисел компараторы соединяют каскадом.
Мультиплексоры
Мультиплексор (MUX) – комбинационное устройство обеспечивающее передачу в желаемом порядке цифровой информации поступающей по нескольким входам на один выход.
Схематически MUX можно изобразить в виде коммутатора, обеспечивающего подключение одного из информационных входов к выходу устройства, в зависимости от сигнала на адресном входе.
| А(адресный вход) | Y |
| 0 | X1 |
| 1 | X2 |
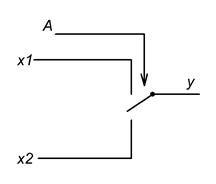
Рис. Схематическое представление MUX и его таблица истинности.
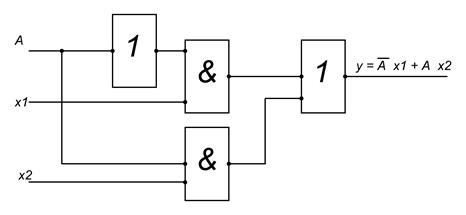
Рис. Логическая схема MUX
Входные логические сигналы X поступают на входы коммутатора и через коммутатор передаются на выход Y. Управление коммутатором осуществляется входной логической схемой. На вход логической схемы подаются адресные сигналы A (Adress). Мультиплексоры могут иметь дополнительный управляющий вход Е (Enable), который может выполнять стробирование выхода Y. Эти входы используются для расширения функциональных возможностей MUX, таких как наращивание разрядности и синхронизации с другими устройствами. Сигналы на разрешающих входах могут разрешать либо запрещать подключение определённого входа к выходу устройства.
Основой данной схемы являются две схемы совпадения на элементах И, которые при логическом уровне «1» на одном из своих входов повторяют на входе то, что есть на другом входе. Для наращивания числа входов мультиплексоры соединяют каскадно.
Логическая схема такого каскадного соединения:
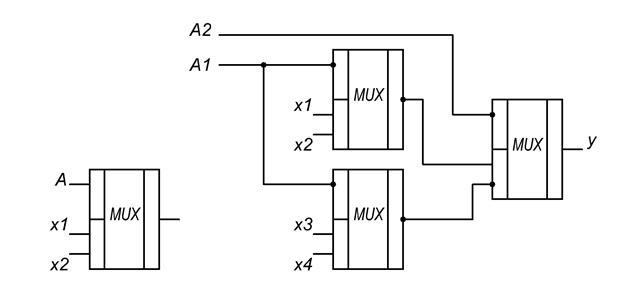
Рис. Обозначение MUX в схеме и каскадное соединение MUX
| Адресные входы | У | |
| А2 | А1 | |
| 0 | 0 | х1 |
| 0 | 1 | х2 |
| 1 | 0 | х3 |
| 1 | 1 | х4 |
Мультиплексоры являются универсальным логическим устройством, на основе которых создают различные комбинационные и последовательные схемы MUX могут использоваться в делителях частоты, триггерных устройствах, сдвигающих устройствах.
Их так же часто используют для преобразования двоичного кода в последовательный. Для этого на информационные входы подают параллельный двоичный код, а сигналы на адресные входы падают в такой последовательности, чтобы к выходу поочерёдно подключались входы начиная с первого и заканчивая последним.
Мультиплексоры могут быть полными и не полными.
n = 2m – уравнение полного мультиплексора,
где n – число информационных входов, m – число адресных входов.
Демультиплексоры.
Демультиплексор (DMX) – устройство, в котором сигналы с одного информационного входа поступают в желательной последовательности от сигнала на адресных входах. Таким образом, демультиплексор выполняет преобразование, обратное действию мультиплексора.
Представим демультиплексор аналогично мультиплексору с помощью схематического представления , логической схемы и таблицы истинности.
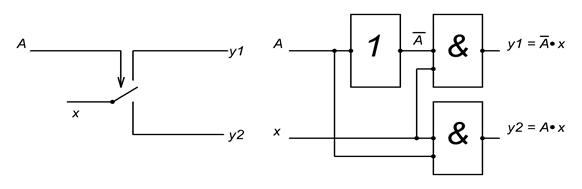
Рис.1 Схематическое представление DMX и логическая схема DMX
Для наращивания числа выходов DMX соединяют каскадно.
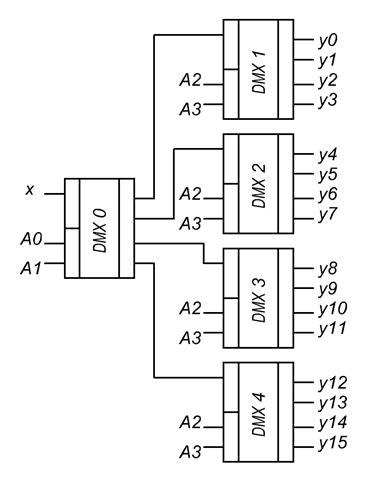
Рис.2 Каскадное соединение DMX.
При наличии на адресных шинах А0 и А1 нулей вход х подключается к верхнему выходу DMX0 и в зависимости от состояния адресных шин А2 и А3 вход х может быть подключён к одному из 4х выходов DMX1 и т.д. по всем возможным комбинациям. Таким образом адресные входы А0 и А1 определяют в какой из DMX уйдёт информация, а адресные входы А2 и А3 определяют на какой именно выход.
Функции DMX сходны с функциями дешифратора. Дешифратор можно рассматривать как DMX у которого информационный вход поддерживает напряжение выходов в активном состоянии , адресные входы выполняют роль входов дешифратора. Современные технологи позволяют строить двунаправленные ключи, которые обладают возможностью пропускать ток в обоих направлениях и передавать ток не только цифровые, но и аналоговые сигналы. Благодаря этому можно строить MUX – DMX, которые обозначаются MX.
Основные типы триггеров.
SR-триггер
SR-триггер имеет два информационных входа Set и Reset. Подача на вход S сигнала единицы (S = 1), а на вход R нуля (R = 0) устанавливает на выходе триггера сигнал Q = 1. Если наоборот S = 0 и R = 1 сигнал на выходе триггера станет Q = 0. При подаче на оба входа нулей (R = 0, S = 0) состояние триггера не измениться – будет происходить хранение информации. Функционирование SR-триггера определяется уравнениями:
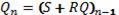
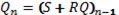; QR = 0.
Для SR-триггера комбинация S= I и R = 1 является запрещенной. После такой комбинации информационных сигналов состояние триггера будет неопределенным: на его выходе Q может быть 0 или 1. SR-триггеры могут быть асинхронными или синхронными, в последнем случае у них имеется вход С).
Существуют разновидности SR -триггеров, называемые E-, R- и S-триггерами. лля которых сочетание S = R = 1 не является запрещенным.
Е-триггер при S = R = 1 не изменяет своего состояния (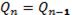 
).
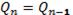S-триггер при S = R = 1 устанавливается в состояние Q = 1,
R-триггер при S = R = 1 устанавливается в состояние Q = 0.
JK-триггер
JK-триггер имеет также два информационных входа Jump и Кeep. Подобно SR-триггеру. в JК-триггере J и К - это входы установки выхода Q триггера в состояние 1 или 0. Однако, в отличие от sr-триггера, в JK-триггере наличие J = K = 1 приводит к переходу выхода Q триггера в противоположное состояние .Условие функционирования JK-триггера имеет вид:
.
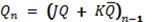
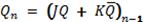JK-триггеры синхронизируются только перепадом потенциала на входе С.
D-триггер
D-триггер (Delay), или триггер задержки, при поступлении синхросигнала на вход С устанавливается в состояние, соответствующее потенциалу на входе D. Уравнение функционирования D-триггера имеет вид:
.
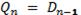
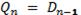Это уравнение показывает, что выходной сигнал Qn изменяется не сразу после изменения входного сигнала D, а только с приходом синхросигнала, т. е. с задержкой на один период импульсов синхронизации (Delay — задержка). Синхронизация – триггера может осуществляться импульсом или фронтом.
Т-триггер
Т-триггер, или счетный триггер, изменяет состояние выхода по фронту импульса на входе С. Кроме синхровхода С, Т-триггер может иметь подготовительный вход Т. Сигнал на этом входе разрешает (при Т=1) или запрещает (при Т=0) срабатывание триггера от фронтов импульсов на входе С. Функционирование Т-триггера определяется уравнением:
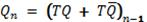
Из этого уравнения следует, что при T = 1 соответствующий сигнал на входе триггера переводит триггер в противоположное состояние. Частота изменения потенциала на входе T в 2 раза меньше частоты импульса на входе С. Это свойство позволяет строить на основе Т-триггеров двоичные счётчики, поэтому его называют счётным.
Асинхронные счетчики.
Асинхронный суммирующий счётчик (АСС) можно выполнить на счётных триггерах любого типа. В большинстве случаев используется JK или D триггер.
Представим суммирующий трёх разрядный счётчик.
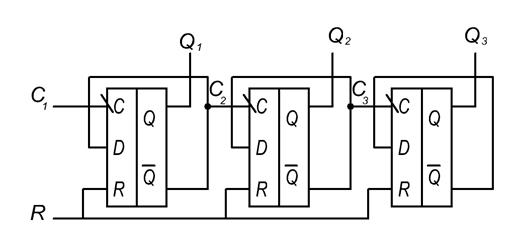
Рис.1 Схема трёхразрядного асинхронного счётчика.
При поступлении счётных импульсов на вход С1 триггеры будут изменять своё состояние описываемое последовательно возрастающими числами.
| n | Q3 | Q2 | Q1 |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 |
| 4 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 6 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 |
Таблица состояний триггера.
Для приведения счетчика в начальное состояние используется сигнал сброса, поступающий одновременно во все счётчики.
При построении асинхронного вычитающего счетчика достаточно заменить выходы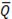 
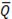триггеров на прямые выходы Q. В этом случае при поступлении импульса сброса R на всех выходах счетчика установятся единичные уровни, а при поступлении счетных импульсов на вход С1 триггеры счетчика будут изменять свои состояния, описываемые последовательно убывающими двоичными числами.
Для построения асинхронного реверсивного счетчика, который может работать как в режиме суммирования, так и в режиме вычитания, можно с помощью логической схемы обеспечить подачу сигналов с инверсного выхода Q при суммировании или с прямого выхода Q — при вычитании от предыдущего триггера на счетный вход последующего.
Эта схема включается между выходом одного разряда счетчика и входом другого и, в зависимости от управляющих сигналов — сложение (U) или вычитание (D), на вход последующего разряда поступает сигнал переноса Р или сигнал займа Z.
В асинхронном счетчике с приходом каждого последующего импульса на вход С1| переключаются сразу несколько триггеров. Однако переключение этих триггеров происходит не одновременно, а с некоторой задержкой относительно друг друга. Это приводит к задержке в установлении выходного кода после поступления счетного импульса на вход С1. При большом числе разрядов счетчика задержка выходного сигнала может быть значительной и сравнимой с периодом поступления счетных импульсов на вход С1. Поэтому в качестве первого триггера нужно использовать самый быстрый, а быстродействие других триггеров может мыть ниже.
Синхронные счетчики.
Для построения синхронных счетчиков используют различные типы счетных синхронных триггеров. Приведём схемы одноразрядных синхронных счетчиков.
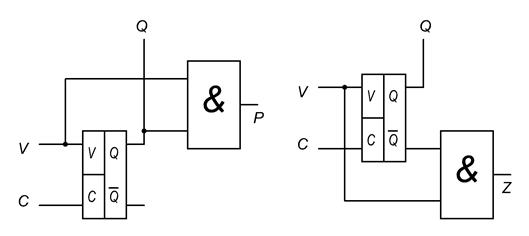
| Рис.1 Суммирующий одноразрядный синхронный счётчик. | Рис.2 Вычитающий одноразрядный синхронный счётчик. |
Аналого-цифровые (ЦАП)
и цифро-аналоговые (ЦАП) преобразователи.
В.Г.Николаев,
ведущий научный сотрудник Учреждения Российской академии наук Института химии и технологии редких элементов и минерального сырья
им. И.В. Тананаева Кольского научного центра РАН,
доктор технических наук, старший научный сотрудник
А.Е. Иванов,
доцент кафедры химических технологий и строительного материаловедения
Апатитского филиала Мурманского государственного технического университета, кандидат химических наук, доцент
Шейко Е.М., Енбаева Е.С.
Электроника. Часть II: Цифровая электроника: учеб. пособие. – Апатиты: Изд. Кольского филиала ПетрГУ, 2010. – 103 с.
Учебное пособие содержит курс лекций по дисциплине «Электроника», читаемый студентам Кольского филиала Петрозаводского государственного университета. В части II пособия изложены основы цифровой электроники, основные понятия об устройствах на ее основе. В доступной форме излагаются физические основы работы и технические показатели наиболее типичных и распространенных электронных приборов, а также принципы построения простейших электронных схем.
Издание подготовлено в соответствии с государственными образовательными стандартами и предназначено для студентов очной и заочной форм обучения техническим специальностям: 140402 «Теплофизика», 210301 «Радиофизика и электроника», 140201 «Высоковольтные электроэнергетика и электротехника», 140604 «Электропривод и автоматика промышленных установок и технологических комплексов», 130401 «Физические процессы (горного или нефтегазового) производств, 130403 «Открытые горные работы», 130404 «Подземная разработка месторождений полезных ископаемых», 130405 «Обогащение полезных ископаемых», 020302 «Геофизика». Учебное пособие может быть полезно аспирантам и инженерам.
Табл.− 6, ил. − 69, библиогр. − 15 назв.
УДК 622:620.2
ББК 30.3
Е.М. Войтышина, Е.С. Енбаева, 2010
Кольский филиал Петрозаводского
государственного университета, 2010
• Алгебра логики.
В устройствах цифровой электроник используются элементы входные выходные сигналы которых могут принимать лишь 2 значения: логический нуль и логическая единица. Для описания алгоритмов работы и структуры логических схем используют алгебру логики. Алгебра логики также называется булевой алгеброй. В алгебре логики определены отношение эквивалентности (=) и три операции : логическое отрицание (НЕ); логическое сложение (ИЛИ); логическое умножение (И).
Рис. Условное обозначение основных логических операций.
В булевой алгебре широко применяются таблицы истинности. Таблица истинности – это таблица, содержащая все возможные комбинации значений входных переменных и соответствующие им значение функции. Она состоит из n переменных; 2n строк; n+1 столбцов.
Приведём таблицы истинности основных логических операций.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим пример:
.
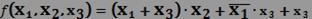
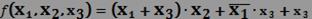| x1 | x2 | x3 | x1+x3 |
|
|
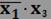
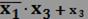
| y |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
• Преобразователи кодов.
Семисегментный индикатор.
Операция изменения кода числа называется его перекодированием. Интегральные микросхемы, выполняющие эти операции, называются преобразователями кодов.
Преобразователи кодов бывают простые и сложные. К простым относятся преобразователи, которые выполняют стандартные операции изменения кода чисел, например, преобразований двоичного кода в одинарный или обратную операцию. Сложные преобразователи кодов выполняют нестандартные преобразования кодов и их схемы приходится разрабатывать каждый раз с помощью алгебры логики.
Будем считать, что преобразователи кодов имеют п входов и к выходов. Соотношения между п и к могут быть любыми: п=к, п<к и п>к. При преобразовании кода чисел с ними могут выполняться различные дополнительные операции, например, умножение на весовые коэффициенты. Примером невесового преобразования является преобразование двоично-десятичного кода в двоичный. Весовые преобразователи кодов используются при преобразовании числовой информации.
В качестве примера рассмотрим преобразователь двоичного кода в код управления семисегментным цифровым индикатором. Сам индикатор представляет собой полупроводниковый прибор, в котором имеются семь сегментов, выполненных из светодиодов. Включением и выключением отдельных сегментов можно получить светящееся изображение отдельных цифр или знаков.
Рис.1 Схема семисегментного индикатора.
Каждой цифре соответствует свой набор включения определенных сегментов индикатора. В таблице также приведены двоичные коды соответствующих цифр. Такие индикаторы позволяют получить светящееся изображение не только цифр от 0 до 9, но других знаков, используемых в 8- и 16-ричной системах счисления.
| n | Сегменты Yk | Код Xk | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 4 | 2 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 3 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 6 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
Таблица соответствия кодов семисегментного индикатора.
Шкальные индикаторы представляют собой линейку светодиодов с одним общим анодом или катодом. Преобразователи двоичного кода в код управления шкальным индикатором обеспечивают перемещение светящегося пятна, определяемое двоичным кодом на адресном входе.
Матричные индикаторы представляют собой наборы светодиодов, расположенных по строкам и столбцам. Наиболее распространенными матричними индикаторами являются индикаторы, имеющие 5 столбцов и 7 строк (формат 5x7). Количество светодиодов в таких матричных индикаторах равно 35. Управление такими индикаторами производится путем выбора номера строки и номера столбца, на пересечении которых находится нужный светодиод.
Для управления матричными индикаторами выпускаются микросхемы, в которых положение светодиода задается номерами столбца i и строки j, причем не все комбинации i и j используются. Такие преобразователи кодов называются неполными.
Примерами простейших преобразователей кодов, которые широко применяются в цифровых устройствах, являются шифраторы и дешифраторы.
Шифратор и Дешифратор.
Шифратором называют кодовый преобразователь, который имеет п входов и k выходов, и при подаче сигнала на один из входов (обязательно только на один) на выходах появляется двоичный код возбужденного входа. Очевидно, что число выходов и входов в полном шифраторе связано соотношением n=2k.
Рассмотрим принцип построения шифратора на примере преобразования 8-разрядного единичного кода в двоичный код. Приведём схему шифратора и его условное схематичное обозначение.
Рис.1 Схема шифратора и его схематичное обозначение.
Если все входные сигналы имеют нулевое значение, то на выходе шифратора будем иметь нулевой код YQ=Yl = Y2=0. Младший вход с весовым коэффициентом, равным 1, должен возбуждаться при входном сигнале на любом из нечётных входов(1,3,5,7), так как все нечетные номера в двоичном представлении содержат единицу в младшем разряде.
Следующий выход имеет весовой коэффициент два. Он должен возбуждаться при подаче сигналов на входы с номерами 2, 3, 6, 7, т. е. с номерами, имеющими в двоичном представлении единицу во втором разряде.
Старший разряд двоичного кода формируется из входных сигналов с номерами 4, 5, 6 и 7, т. е. из четырех старших разрядов единичного кода. Все рассмотренные состояния шифратора приведем в таблицу.
| X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | Y2 | Y1 | Y0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
Таблица состояний шифратора.
Как следует из выполненного построения, при помощи шифратора можно сократить (сжать) информацию для передачи ее по меньшему числу линий связи, так как к<п. Очевидно, что максимальное число входов шифратора не может превышать количество возможных комбинаций выходных сигналов, т. е. необходимо выполнение условия n ≤ 2k.
В цифровых системах с помощью шифраторов обеспечивается связь между различными устройствами посредством ограниченного числа линий связи. Так, например, в кнопочных пультах управления ввод числовых данных обычно выполняется в унитарном коде посредством нажатия одной из десяти кнопок, а ввод данных в микропроцессор выполняется в двоичном коде. Для такого преобразования используют шифратор из «10 в 4» Поскольку 4х разрядный шифратор имеет не 10 а 16 возможных комбинаций, то такой шифратор является не полным.
Обратное преобразование, т. е. восстановление информации в первоначальном виде можно выполнить с помощью прибора который называется дешифратор.
Дешифратором называют преобразователь двоичного n-разрядного кода в унитарный 2n-разрядный код, все разряды которого, за исключением одного, равны нулю. Дешифраторы бывают полные и неполные. Для полного дешифратора выполняется условие:
N=2n, (15.2)
где n — число входов, а N — число выходов.
В неполных дешифраторах имеется n входов, но реализуется N<2n выходов, так, например, дешифратор, имеющий 4 входа и 10 выходов будет неполным, а дешифратор, имеющий 2 входа и 4 выхода, будет полным.
Рассмотрим принцип построении дешифратора на примере преобразования разрядного двоичного кода в унитарный код. Для полного дешифратора можно записать восемь упорядоченных уравнений:
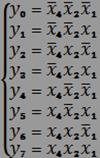
Рис.2 Система уравнений дешифратора его схематичное обозначение;
Рис.3 Схема дешифратора.
Сумматор.
Сумматор является комбинационным устройством, предназначенным для сложения чисел.
Комбинационные устройства – устройства, на выходах которого в некоторый момент времени однозначно определяются входными сигналами в этот же момент.
Для сложения 2х одноразрядных чисел А и В необходимо реализовать устройство которое называется полусумматором. Приведём логическую схему и таблицу истинности полусумматора. Отметим, что относительно столбца S реализуется логическая функция “исключающего ИЛИ ”.
Рис.1 Логическая схема полусумматора
| A | B | S | P |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Таблица истинности полусумматора
Поскольку полусумматор имеет только 2 выхода, то он может использоваться для суммирования лишь в младшем порядке. При суммировании 2х многоразрядных чисел каждого разряда кроме младшего необходимо использовать устройство имеющее дополнительно вход переноса Pвх. Такое устройство называют полным сумматором и его можно представить, как объединение двух полусумматоров логической операцией ИЛИ. Соединяя особым образом полусумматоры и сумматоры можно получить устройство для сложения многоразрядных чисел.
Рис.2 Параллельный сумматор.
При вычитании чисел необходимо проделать ряд дополнительных операций. Сначала вычитаемое число записываем в обратном коде, причём уменьшаемое число остаётся прежним а операция «–» заменяется на «+».
Апр – Впр = Апр + Вобр.
• Если А>В т.е. ответ положительное число, то при формируется единица в старшем разряде а к результату суммы необходимо добавить единицу к младшему разряду.
Апр – Впр = Апр + Вобр = Sпр
• Если А<В т.е. ответ отрицательный то 1 единица в старшем разряде не формируется, а результат суммы при этом представлен в обратном коде.
Апр – Впр = Апр + Вобр = Sобр
Цифровые компараторы.
Цифровые компараторы выполняют сравнение 2х чисел заданных в двоичном коде. Они могут определять равенство двоичных чисел А и В с одинаковым количеством разрядов, либо в виде неравенства.
Компараторы имеют три выхода. На рисунке представлена схема одноразрядного компаратора, представляющая собой структуру логического элемента.
Рис.3 Логическая схема компаратора.
Сравнение чисел происходит попарно, начиная со старшего разряда. В случае неравенства старших разрядов будут задействованы выходы либо D либо С, в случае равенства старших разрядов сравнение переходит в следующий разряд, и так до младшего, при условии равенства всех остальных. В случае если 2 числа равны будет задействован выход F.
Компараторы выполняются как самостоятельные микросхемы, чаще всего 4х разрядные, а для наращивания разрядов сравниваемых чисел компараторы соединяют каскадом.
Мультиплексоры и демультиплексоры.
Мультиплексоры
Мультиплексор (MUX) – комбинационное устройство обеспечивающее передачу в желаемом порядке цифровой информации поступающей по нескольким входам на один выход.
Схематически MUX можно изобразить в виде коммутатора, обеспечивающего подключение одного из информационных входов к выходу устройства, в зависимости от сигнала на адресном входе.
| А(адресный вход) | Y |
| 0 | X1 |
| 1 | X2 |
Рис. Схематическое представление MUX и его таблица истинности.
Рис. Логическая схема MUX
Входные логические сигналы X поступают на входы коммутатора и через коммутатор передаются на выход Y. Управление коммутатором осуществляется входной логической схемой. На вход логической схемы подаются адресные сигналы A (Adress). Мультиплексоры могут иметь дополнительный управляющий вход Е (Enable), который может выполнять стробирование выхода Y. Эти входы используются для расширения функциональных возможностей MUX, таких как наращивание разрядности и синхронизации с другими устройствами. Сигналы на разрешающих входах могут разрешать либо запрещать подключение определённого входа к выходу устройства.
Основой данной схемы являются две схемы совпадения на элементах И, которые при логическом уровне «1» на одном из своих входов повторяют на входе то, что есть на другом входе. Для наращивания числа входов мультиплексоры соединяют каскадно.
Логическая схема такого каскадного соединения:
Рис. Обозначение MUX в схеме и каскадное соединение MUX
| Адресные входы | У | |
| А2 | А1 | |
| 0 | 0 | х1 |
| 0 | 1 | х2 |
| 1 | 0 | х3 |
| 1 | 1 | х4 |
Мультиплексоры являются универсальным логическим устройством, на основе которых создают различные комбинационные и последовательные схемы MUX могут использоваться в делителях частоты, триггерных устройствах, сдвигающих устройствах.
Их так же часто используют для преобразования двоичного кода в последовательный. Для этого на информационные входы подают параллельный двоичный код, а сигналы на адресные входы падают в такой последовательности, чтобы к выходу поочерёдно подключались входы начиная с первого и заканчивая последним.
Мультиплексоры могут быть полными и не полными.
n = 2m – уравнение полного мультиплексора,
где n – число информационных входов, m – число адресных входов.
Демультиплексоры.
Демультиплексор (DMX) – устройство, в котором сигналы с одного информационного входа поступают в желательной последовательности от сигнала на адресных входах. Таким образом, демультиплексор выполняет преобразование, обратное действию мультиплексора.
Представим демультиплексор аналогично мультиплексору с помощью схематического представления , логической схемы и таблицы истинности.
Рис.1 Схематическое представление DMX и логическая схема DMX
Для наращивания числа выходов DMX соединяют каскадно.
Рис.2 Каскадное соединение DMX.
При наличии на адресных шинах А0 и А1 нулей вход х подключается к верхнему выходу DMX0 и в зависимости от состояния адресных шин А2 и А3 вход х может быть подключён к одному из 4х выходов DMX1 и т.д. по всем возможным комбинациям. Таким образом адресные входы А0 и А1 определяют в какой из DMX уйдёт информация, а адресные входы А2 и А3 определяют на какой именно выход.
Функции DMX сходны с функциями дешифратора. Дешифратор можно рассматривать как DMX у которого информационный вход поддерживает напряжение выходов в активном состоянии , адресные входы выполняют роль входов дешифратора. Современные технологи позволяют строить двунаправленные ключи, которые обладают возможностью пропускать ток в обоих направлениях и передавать ток не только цифровые, но и аналоговые сигналы. Благодаря этому можно строить MUX – DMX, которые обозначаются MX.
Дата: 2018-12-21, просмотров: 282.
